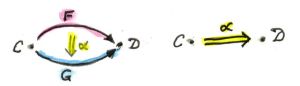Haskell

Archived Posts from this Category

January 21, 2016

Tambara Modules

Posted by Bartosz Milewski under Category Theory, Haskell
[3] Comments

I came in contact with Tambara modules when working on a categorical understanding of lenses. They were first mentioned to me by Edward Kmett, who implemented their Haskell version, Data.Profunctor.Tambara. Recently I had a discussion with Russell O’Connor about profunctor lenses. He then had a discussion with James “xplat” Deikun, who again pointed out the importance of Tambara modules. That finally pushed me to study Tambara’s original paper along with Pastro and Street’s generalizations of it. These are not easy papers to read; so, to motivate myself, I started writing this post with the idea of filling in the gaps in my education and providing some background and intuitions I gather in the process. Trying to explain things always helps me understand them better. I will also sketch some of the proofs — for details, see the original papers.

The general idea is that lenses are used to access components of product data types, whereas prisms are used with coproduct (sum) data types. In order to unify lenses and prisms, we need a framework that abstracts over products and coproducts. It so happens that both are examples of a tensor product. Tensors have their roots in vector calculus, so I’ll start with a little refresher on it, to see where the intuitions come from. Tensors may also serve as objects upon which we can represent groups or monoids.

The next step is to define a monoidal category, where the tensor product plays a role analogous to group (actually, monoid) action. Tensor categories are built on top of (or, enriched over) monoidal categories.

We can define monoidal action on tensor categories — analogous to representations of groups on tensor fields. One particular tensor category of interest to us is the category of distributors (profunctors). Distributors equipped with a tensor action are the subject of Tambara’s paper. It turns out that tensor action on distributors is directly related to profunctor strength, which is the basis of the general formulation of Haskell lenses and prisms.

Vectors and Tensors

We all have pretty good idea of what a vector space is. It’s a sets of vectors with vector addition and with multiplication by numbers. The numbers, or scalars, come from some field K (for instance real or complex numbers). These operations must obey some obvious rules. For instance, multiplying any vector by 1 (the multiplicative unit of K) gives back the same vector:

1v = v

Then there are the linearity conditions (α and β are scalars from K, and v and w are vectors):

αv + βv = (α + β)v
α(v + w) = αv + αw

which can be used to prove that every vector space has a basis — a minimal set of vectors whose linear combinations generate the whole space.

In other words, any vector v can be written as a combination of base vectors e_i:

v = Σ α_ie_i

where Σ represents the sum over all is.

Or we can go the other way: We can start with a set B that we call the base set, define formal addition and multiplication, and then create a free structure containing all formal combinations of base vectors. Our linearity laws are then used to identify equivalent combinations. This is called a free vector space over B. The advantage of this formulation is that it generalizes easily to tensor spaces.

A tensor space is created from two or more vector spaces. The elements of a tensor space are formal combinations of elements from the constituent vector spaces. Those “formal combinations” can be described in terms of a tensor product. A tensor product V ⊗ W of two vector spaces is a mapping of the cartesian product V × W (a set of pairs of vectors) to the free vector space built on top of V and W, with the appropriate identifications:

(v, w) + (v', w) = (v + v', w)
(v, w) + (v, w') = (v, w + w')
α(v, w) = (αv, w) = (v, αw)

A tensor product can also be defined for mappings between vector spaces. Given four vector spaces, V, W, X, Y, we can consider linear maps between them:

f :: V -> X
g :: W -> Y

The tensor product of these maps is a linear mapping between tensor products of the appropriate spaces:

(f ⊗ g) :: V ⊗ W -> X ⊗ Y
(f ⊗ g)(v ⊗ w) = (f v) ⊗ (g w)

Vector spaces form a category Vec with linear maps as morphisms. Tensor product can then be defined as a bifunctor from the product category Vec × Vec to Vec (so it also maps pairs of morphisms to morphisms).

Given a vector space V, we can also define a dual space V^* of linear functions from V to K (remember, K is the field from which we get our scalars). The action of an element f of V^* on a vector v from V is called evaluation (or, in physics, contraction):

eval :: V^* ⊗ V -> K
eval f v = f v

Given a basis e_i in V, the canonical basis in V^* is a set of functions e^*_i such that:

eval e^*_i e_j = δ_ij

where δ_ij is 1 for i=j and 0 otherwise (the Kronecker delta). Seen as a matrix, δ is a unit matrix. It almost looks like the dual space provides the “inverses” of vectors. This is an important intuition.

A general tensor space supports tensor products involving a mixture of vectors and dual vectors (linear maps). In physics, this allows the construction of mixed covariant and contravariant tensors.

The dual to evaluation is called co-evaluation. In finite dimensional vector spaces, it’s a mapping:

coeval :: K -> V ⊗ V^*
coeval α = Σ α e_i ⊗ e^*_i

It takes a scalar α and creates a tensor using basis vectors and their duals. Tensors can be summed and multiplied by scalars.

One obvious generalization of vector (and tensor) spaces is to replace the field K with a ring. A ring has addition, subtraction, and multiplication, but it doesn’t have division.

Groups and Monoids

Groups were originally introduced in terms of actions on vector spaces. The action of a group element g on a vector v maps it to another vector in the same vector space. This mapping is linear:

g (αv + βw) = α (g v) + β (g w)

Because of linearity, group action is fully determined by the transformation of basis vectors. An element of a group acting on a vector v=Σv_ie_i produces a vector w that can be decomposed into components w=Σw_ie_i:

w_i = Σ g_ij v_j

The numbers g_ij form a square matrix. The mapping of group elements to these matrices is called the representation of the group. The group of rotations in two dimensions, for instance, can be represented using 2×2 matrices of the form:

|  cos α  sin α |
| -sin α  cos α |

This is an example of a representation of an infinite continuous group called SO(2) (Special Orthogonal group in 2-d).

Applying a group element to a vector produces another vector that can be acted upon by another group element, and so on. You can forget about elements acting on vectors and define group multiplication abstractly. A group is a (potentially infinite) set of elements with a binary operation that is associative, has a neutral (identity) element, and an inverse for every element. It turns out that the same group may have many representations in vector spaces. Associativity and identity in the group happen also to be the basic properties defining a category — invertibility, though, is not. It should come as no surprise that categorists prefer the simpler monoid structure and consider a group a more specialized versions of it.

You get a monoid by abandoning the requirement that all elements of a group have an inverse. Or, even more abstractly, you can define a monoid as a single-object category, where the composition of (endo-) morphisms defines multiplication, and the identity morphism is the neutral element. These two definitions are equivalent because endomorphisms form a set — the hom-set — that can be identified with the set of elements of the monoid. The hom-set has composition of endomorphisms, which can be identified with the binary monoidal operation.

Some groups and monoids are commutative (for instance integer addition); others are not (for instance string concatenation). The commutative subgroup or submonoid is called the center of the group or monoid. Elements of the center must commute with all elements of the group, not only among themselves.

You may also think of representing a group (or a monoid) as acting on itself. There are two ways of doing that: the left action and the right action. The action of a group element g can be represented as transforming the whole group by multiplying each element by g on the left:

L_g h = g * h

or on the right:

R_g h = h * g

Such a transformation results in a reshuffling of the elements of the group. Each g defines a different reshuffling. A reshuffling (for finite sets) is called a permutation, and one of the fundamental theorems in group theory, due to Cayley, says that every group is isomorphic to some permutation group.

Cayley’s theorem can be generalized to monoids. Instead of the reshuffling of elements we then talk about endomorphisms. Every monoid defined as a set M with multiplication and unit can be represented as a submonoid of endomorphisms of that set.

This equivalence is well know to Haskell programmers. Monoid multiplication may be represented as a binary function (multiplication):

mappend :: (M, M) -> M

or, after currying, as a function returning an endomorphism:

mappend :: M -> (M -> M)

The unit element, mempty becomes the identity endomorphism, id.

Monoidal Category

We’ve seen that a monoid can be defined as a set of elements with a binary operation, or as a single-object category. The next step in this ladder of abstractions is to rethink the idea of forming pairs of elements for a binary operation. When dealing with sets, the pairs are just elements of the cartesian product.

In a more general categorical setting, cartesian product may be replaced with categorical product. Multiplication is just a morphism from the product m×m to the object itself m. But how do we select the unit element of m? Categorical objects have no structure. So instead we use a generalized element, which is defined as a morphism from the terminal object (in set, that would be the singleton set) to m.

A monoid can thus be defined as an object m in a category that has products and the terminal object t together with two morphisms:

mult :: m × m -> m
unit :: t -> m

But what if the category C in which we are trying to define a monoid doesn’t have a product or the terminal object? No problem! Instead of categorical product we’ll define a bifunctor ⊗:

⊗ :: C × C -> C

It’s a functor from the product category C×C to C. It’s called a tensor product by analogy with the vector space construction we started with. As a functor, it also defines a mapping of morphisms.

Instead of the terminal object, we just pick one special object i and define a generalized unit as a morphism from i to m.

The tensor products must fulfill some obvious conditions like associativity and the unit laws. We could define them by equalities, e.g.,

(a ⊗ b) ⊗ c = a ⊗ (b ⊗ c)
i ⊗ a = a = a ⊗ i

The snag is that our prototypical tensor product, the cartesian product, doesn’t satisfy those identities. Consider the Haskell implementation of the cartesian product as a pair type, with the unit element as the unit type (). It’s not exactly true that:

((a, b), c) = (a, (b, c))
((), a) = a = (a, ())

However, it’s almost true. The types on both sides of the equations are isomorphic, as can be shown by defining polymorphic functions that mediate between those terms. In category theory, those polymorphic functions are replaced by natural transformations.

A category in which associativity and unit laws of the tensor product can be expressed as equalities is called a strict monoidal category. A category in which these laws are imposed only up to natural isomporphisms is called non-strict monoidal category. The three isomorphisms are called the associator α, the left unitor λ, and the right unitor ρ, respectively:

α :: (a ⊗ b) ⊗ c -> a ⊗ (b ⊗ c)
λ :: i ⊗ a  -> a
ρ :: a ⊗ i -> a

(They all must have inverses.)

A useful example of a strict monoidal category is the category of endofunctors of some category C. We use functor composition for tensor product. Composition of two endofunctors F and G is always well defined and it produces another endofunctor G∘F. The unit of this monoidal category is the identity functor Id. Strict associativity and unit laws follow from the definition of functor composition and the definition of the identity functor.

In some categories it’s possible to define an exponential object a^b, which represents a set of morphisms from b to a. The standard way of doing it is through the adjunction:

C(a × b, c) ≅ C(b, c^a)

Here, C(x, y) represents the hom-set from x to y. The two hom-sets in the adjunction must be naturally isomorphic. In general, an adjunction is between two functors L and R:

C(L b, c) ≅ C(b, R c)

Here the two functors are:

L_a b = a × b
R_a c = c^a

This definition of the exponential object can be extended to monoidal categories by replacing categorical product with the tensor product:

C(a ⊗ b, c) ≅ C(b, c^a)

In a monoidal category we can also define a left exponential:

C(a ⊗ b, c) ≅ C(a, ^bc)

(if the tensor product is symmetric, or weakly symmetric — up to a natural isomorphism — these two exponentials coincide).

There is an equivalent definition of an adjunction through unit η and counit ε — two natural transformations. These transformations are between the composition of two adjoint functors and the identity functor:

η :: Id -> R ∘ L
ε :: L ∘ R -> Id

This comes even closer to convincing us that exponentiation is the inverse of a product.

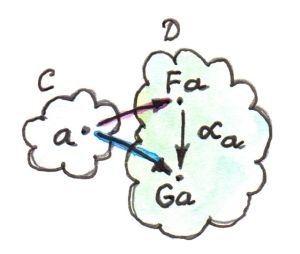
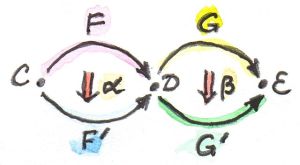
As it often happens, having equivalent definitions of the same thing may lead to different generalizations. We’ve seen that the category of endofunctors in some category C is a (strict) monoidal category. We can pick two endofunctors F and G and define two natural transformations:

ε :: G ∘ F -> Id
η :: Id -> F ∘ G

If such transformations exist, the pair F and G form an adjunction, F being left adjoint to G.

This definition can be extended to any monoidal product, not just composition. In a tensor category A, we have the unit object i, and we can try to define two morphisms:

ε :: a ⊗ a' -> i
η :: i -> a' ⊗ a

The pair of objects a and a' together with the morphisms ε and η are called a duality. A category is called rigid or autonomous if there is a dual for every object. A duality gives rise to an adjunction:

Hom(ax, y) ≅ Hom(x, a'y)

Comparing this with the exponential adjunction, we see that the dual of a acting on y plays the role of y^a. In other words, a' says: raise the object that I’m multiplying to the power of a.

There may be many duals of a, but we can always choose one and denote it as a^c. Multiplying it by y, a^cy is analogous to taking the exponential y^a. It also works like a weak inverse of a because of:

ε :: a a^c -> i
η :: i -> a^c a

Notice that the duality functor, the mapping from a to a^c, is contravariant in a.

Tambara works with rigid categories, whereas Pastro and Street mostly work with closed categories — with exponentials defined for every pair of objects.

Enriched Categories

In traditional category theory hom-sets are just sets. It’s possible, though, to replace hom-sets with something with more structure. Tambara, for instance, uses vector spaces for his hom-sets. In general, hom-sets may be replaced by objects in some other base category — this results in the notion of an enriched category. This base category must have some additional structure in order to support composition in the enriched category.

Composition of morphisms in a regular category is defined in terms of elements of hom-sets. It’s a mapping from a pair of composable morphisms to a morphism. Objects in an arbitrary category might not support the notion of “elements.” So we have to express composition in terms of entire hom-objects rather than their individual elements. The minimal structure necessary for that is a monoidal category. Instead of pairs of morphisms, we’ll operate on a whole (monoidal) product of two hom-objects. Composition is then a morphism in the base category V:

∘ :: A(b, c) ⊗ A(a, b) -> A(a, c)

Here, A(a, b) is an object in V — the hom-object from a to b. Associativity of composition reflects the associativity of the monoidal product (it may be weak!).

Identity morphisms are then “picked” in any A(a, a) by a morphism in V:

id_a :: i -> A(a, a)

where i is the unit object in V. That’s the same trick we used to define generalized elements of objects in a monoidal category. Again, unit laws may be weak.

The main purpose of defining categories is to enable the definitions of functors and natural transformations. Functors map objects and morphisms, so in enriched categories, they have to map objects and hom-objects. Therefore it only makes sense to define enriched functors between categories that are enriched over the same base monoidal category, because that’s where the hom-objects live. An enriched functor must preserve composition — which is defined in terms of the monoidal product — and the identity morphism, which is defined in terms of the monoidal unit.

Similarly, it’s possible to define a natural transformation between two enriched functors F and G that go between two V-enriched categories A and B. The naturality square turns into a naturality hexagon that connects the object A(a, a’) to the object B(F a, G a’) in two different ways. Normally, components of a natural transformation are morphisms between F a and G a. In the enriched setting, there is no way to “pick” individual morphisms. Instead we use morphisms from the identity object in V — generalized elements of hom-objects.

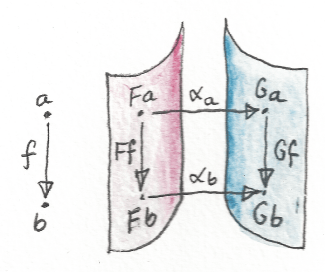
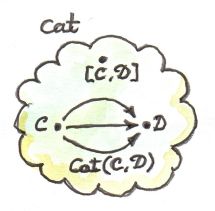
Functors between two given categories A and B (enriched or not) form a category, with natural transformations as morphisms. On the other hand, functors are morphisms in the category Cat of (small) categories. The set of functors between two categories A and B is therefore both a hom-set in Cat and a category. Tambara denotes those hom-categories Hom(A, B). I will use this notation throughout. Otherwise, for hom-sets (and hom-objects in the enriched case) I will use the standard notation C(a, b), where C is the category, and a and b are objects in C.

The starting point of both Tambara and Pastro/Street is a tensor category A. It’s a category enriched over a monoidal category V. There is a separate tensor product defined in A. In Tambara, V is the category of vector spaces with the usual tensor product. In Pastro/Street, V is an arbitrary monoidal category.

Without loss of clarity, the tensor product in A is written without the use of any infix operator. For two objects x and y of A, the product is just xy. A tensor product of two morphisms f::x->x' and g::y->y' is denoted, in Tambara, as fg::xy->x'y' (not to be confused with composition f'∘f). Tambara assumes that associativity and unit laws in A are strict.

Summary

We have the following layers of abstraction:

V is a monoidal category
A is a tensor category enriched over V.

Modules

By analogy with groups and vector spaces, we would like to define the action of a tensor category A on some other category X. As before, we have the choice between left and right action (or both). Let’s start with the left action. It’s a bifunctor:

A × X -> X

In components, the notation is simplified to (no infix operator):

<a, x> -> ax

where a is an object in A and x is an object in X

We want this functor to be associative and unital. In particular:

ix = x

where i is the unit in the tensor category A. The category X with these properties is called a left A module.

Similarly, the right B module is equipped with the functor:

X × A -> X

The interesting case is a bimodule with two bifunctors:

A × X -> X
X × B -> X

The two tensor categories A and B may potentially be different (although they both must be enriched over the same category V as X).

Notice that A itself is a bimodule with both left and right action of A on A defined by the (tensor) product in A.

The usual thing in category theory is to introduce structure-preserving functors between similar categories.

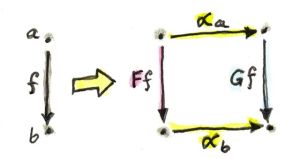
So, if X and Y are two left modules over the same tensor category A, we can define A-linear functors that preserve the action of A. Such functors, in turn, form a category that Tambara calls Hom_A(X, Y) (notice the subscript A). Linearity in this case means that the left action weakly commutes with the functor. In other words, we have a natural isomorphism (here again, left action is understood without any infix operator):

λ_{a, x} :: F (ax) -> a(F x)

This mapping is invertible (it’s an isomorphism).

The same way we can define right- and bi- linear functor categories. In particular an (A, B)-linear functor preserves both the left and the right actions. Tambara calls the category of such functors Hom_{A, B}(X, Y). Linearity in this case means that we have two natural isomorphisms:

λ_{a, x} :: F (ax) -> a(F x)
ρ_{x, b} :: F (xb) -> (F x)b

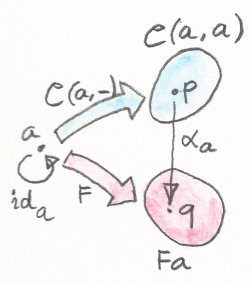
The first result in Tambara’s paper is that, if X is a right A-module, then the category of right linear functors Hom_A(A, X) from A to X is equivalent to X.

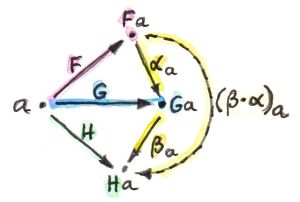
The proof is quite simple. Right to left: Pick an object x in X. We can map it to a functor:

G_x :: A -> X

defined as the right action of a on x:

G_x a = xa

Its linearity is obvious:

ρ_{a, b} :: G_x (ab) -> (G_x a)b

Notice also that evaluating G_x on the identity i of A produces x. So, left to right, we can define the inverse mapping from Hom_A(A, X) to X as the evaluation of the functor at i.

The intuition from group theory is that the (right, in this case) action of the whole group on a fixed x creates an orbit in X. An orbit is the set of points (vectors) that can be reached from x by acting on it with all group elements (imagine a group of rotations around a fixed axis in 3-d — here, orbits are just circles). In our case, we can get an orbit of any x as the image of a linear functor G_x defined above that goes from A (the equivalent of the group) to X (the equivalent of the vector space in which we represent the group). It so happens that the image of any linear functor G from A to X is an orbit. It’s the orbit of the object G i. Any object in the image of G can be reached from G i by the action of some object of A. The image of G consists of objects of the form G a. G a can be rewritten as G (ia) which, by (right) linearity, is the same as (G i)a.

Our intuition that there should be more functors from A to X than there are objects in X fails when we impose the linearity constraint. The functors in Hom_A(A, X) are no longer linearly independent. There is a “basis” in that “space” that is in one-to-one correspondence with the objects of X.

A similar proof works for left modules.

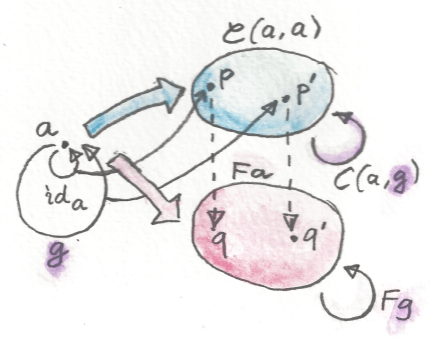
The situation is trickier for bimodules with both left and right action, even if we pick the same tensor category on both sides, that is work with an (A, A)-bimodule.

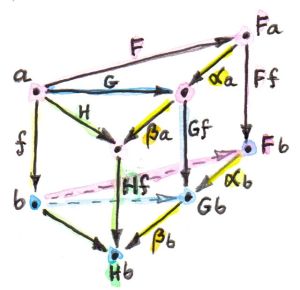
Suppose that we wanted to map X to Hom_{A, A}(A, X). We can still define the (orbit of x) functor G_x as xa with the same ρ_ab. But there is a slight problem with defining λ_ba. We want:

λ_{b a} :: G_x (ba) -> b(G_x a)

which will work if there is a transformation:

xba -> bxa

We would like x to (weakly) commute with b. By analogy with the center of a group, we can define a centralizer Z_A(X) as the category of those objects of X for which there is an isomorphism ω_a between ax and xa. The equivalence of categories in this case is:

Hom_A,A(A, X) ≅ Z_A(X)

So, for any object x that’s in the centralizer of X, we can define our G_x as xa. Conversely, for any (A, A)-linear functor, we can evaluate it at i to get an object of X. This object can be shown to be a member of the centralizer because, for any F in Hom_{A, A}(A, X):

a(F i) = F (a i) = F (i a) = (F i)a

Summary

We have the following layers of abstraction:

V is a monoidal category
A (and B) are tensor categories enriched over V
X is a category enriched over V
X is a module, if the action of A is defined over X (left, right, or both)
Linear functors between X and Y preserve left, right, or bi actions of A (or B).

In particular, bilinear functors from A (with the left and right action of A) to a bimodule X are in one to one correspondence with the centralizer Z_A(X) of X under the action of A.

Distributors

To understand distributors, it helps to know a bit about calculus and/or signal processing. In calculus we deal with functions. Functions can be integrated. We can also have functions acting on functions — or functionals. In particular we can have linear functions on functions. It turns out that a lot of such functionals can be defined through integrals. A linear functional can be expressed as integration of test functions with some density. A density may be a function of two arguments, but a general linear functional may require a generalized density. For instance, the famous Dirac delta “function” cannot be represented as a function, although physicists often write:

f(x) = ∫ δ(x - y) f(y) dy

Such generalized functions are called distributions. Direct multiplication of distributions is ill-defined — the annoying infinities that crop up in quantum field theory are the result of attempts to multiply quantum fields, which are distributions.

A better product can be defined through convolution. Convolutions happen to be at the core of signal processing. If you want to soften an image, you convolve it with a Gaussian density. Convolution with a delta function reproduces the original image. Edge enhancement is done with the derivative of a delta function, and so on.

Convolutions can be generalized to functions over groups:

(f ★ g)(x) = ∫ f(y) g(y^-1x) dλ(y)

where λ is a suitable group measure.

Roughly speaking, distributors are to functors as distributions are to functions. You might know distributors under the name of profunctors. A profunctor is a functor of two arguments, one of them from the opposite category.

p :: X^op × Y -> Set

In a way, a profunctor is a generalization of a bifunctor, at least when acting on objects. When acting on morphisms, a profunctor is contravariant in one argument and covariant in another. In the case of Y being the same as X, this is similar to the hom-functor C(a, b) being contravariant in a and covariant in b. A hom-functor is the simplest example of a profunctor. As we’ll see later, it’s even possible to model the composition of profunctors on composition of hom-functors.

A profunctor acting on two objects produces a set, an object in the Set category (again, generalizing a hom-functor, which is also Set-valued). Acting on a pair of morphisms (which is the same as a single morphism in the product category X^op × Y), a profunctor produces a function.

Distributors can be generalized to categories that are enriched over the same monoidal category V. In that case they are V-valued functors from X^op × Y to V.

Since distributors (profunctors) are functors, they form a functor category denoted by D(X, Y). Objects in a distributor category are (enriched) functors:

X^op × Y -> V

and morphisms are (enriched) natural transformations.

On the other hand, we can treat a distributor as if it were a morphism between categories (it has the right covariance for that). The composition of such morphisms is defined through the coend formula (a coend for profunctors is analogous to a colimit for functors):

(p ∘ q) x y = ∫^z (p x z) ⊗ (q z y)

Here, p and q are distributors:

p :: (X^op × Z) -> V
q :: (Z^op × Y) -> V

The tensor product ⊗ is the product in V (here we explicitly use the infix operator). We “integrate” over the object z in the middle.

This way we can define a bicategory Dist of categories where distributors are morphisms (one-cells) and natural transformations are two-cells. If we also consider regular functors between categories, we get what is called a double category (not to be confused with a 2-category or a bicategory, which are all slightly different).

There is an equivalent way of looking at distributors as a generalization of relations. A relation between two sets is a subset of pairs of elements from those sets. We can model this categorically by treating a set as a discrete category of elements (no morpisms other than identities). The relation between two such sets is a set of formal arrows between their elements — when two elements are related, there is a single arrow between them, otherwise there’s no arrow. Now we can replace sets by categories and define a relation as a bifunctor from those categories to Set. An object from category X is “related” to an object from Y if the bifunctor in question maps them into a non-empty set, otherwise they are unrelated. Since there are many non-empty sets to chose from, there may be many “levels” of relation: ones corresponding to a singleton set, a dubleton, and so on.

We also have to think about the mapping of (pairs of) morphisms from the two categories. Since we would like the opposite relation to be a functor from opposite categories, the symmetric choice is to define a relation as a functor that is contravariant in one argument and covariant in the other — in other words, a profunctor. That way the opposite relation will still be a profunctor, albeit with ops reversed.

One can define the composition of relations. If p relates X to Z and q relates Z to Y then we say that an object x from X is related to an object y from Y if and only if there exists an object z of Z (an object in the middle) such that x is related to z and z is related to y. This existential qualification of z is represented, in category theory, as a coend (an end corresponding to the universal qualifier). Thus, through composition of relations, we recover the formula for the composition of profunctors:

(p ∘ q) x y = ∫^z (p x z) ⊗ (q z y)

There is also a tensor structure in the distributor category D(X, Y) defined by Day convolution, which I’ll describe next.

Summary

We have the following layers of abstraction:

V is a monoidal category
A (and B) are tensor categories enriched over V
X, Y, and Z are categories enriched over V
A distributor is a functor from X^op × Y to V
Distributors may also be treated as “arrows” between categories and composed using coends.

Day Convolution

By analogy with distributions, distributors also have the equivalent of convolution defined on them. The integral is replaced by coend. The Day convolution of two functors F and G, both from the V-enriched monoidal category A to V, is defined as a (double) coend:

(F ⊗ G) x = ∫^a,b A(a ⊗ b, x) ⊗ (F a) ⊗ (G b)

Notice the (here, explicit) use of a tensor product for objects of V (as well as for objects of A and for functors — hopefully this won’t lead to too much confusion). For V equal to Set, this is usually replaced by a cartesian product, but in Haskell this could be a product or a sum. In the formula, we also use the covariant hom-functor that maps an arbitrary object x in A to the hom-set A(a ⊗ b, x). This use of a coend justifies the use of the integral symbol: we are “integrating” over objects a and b in A.

If you squint hard enough you might find similarity between the Day convolution formula and the convolution on a group. Here we don’t have a group, so we have no analog of y^-1x. Instead we define an appropriate “measure” using A(a ⊗ b, _). The convolution formula may be “partially integrated” to give the following equivalent definitions:

(F ⊗ G) x = ∫^b (F ^bx) ⊗ (G b)
(F ⊗ G) x = ∫^a (F a) ⊗ (G x^a)

Here you can see the resemblance to group convolution even better — if you remember that exponentiation can be thought of as the “inverse” of the tensor product. The left and right exponentiations are analogous to the left and right inverses.

The partial integration trick is the consequence of the so-called ninja Yoneda lemma, which can be written as:

F x = ∫^a A(a, x) ⊗ (F a)

Notice that the hom-functor A(a, x) plays the role of the Dirac delta function.

There is also a unit J of Day convolution:

J x = A(i, x)

where i is the monoidal identity object.

Taken together this shows that Day convolution is a tensor product in the category of enriched functors (hence the use of the tensor symbol ⊗).

It’s interesting to see Day convolution expressed in Haskell. The category of Haskell types (which is approximately Set, modulo termination) can be treated as enriched over itself. The tensor product is just the cartesian product, represented either as a pair or a record with multiple fields. In this setting, a categorical coend becomes an existential quantifier, which is equivalent to a universal quantifier in front of the type constructor.

This is the definition of Day convolution from the Edward Kmett’s Data.Functor.Day

data Day f g a = forall b c. Day (f b) (g c) (b -> c -> a)

Here, f and g are the two functors, and forall plays the role of the existential quantifier (being put in front of the data constructor Day). The original hom-set Set(b⊗c, a), has the tensor product replaced by a pair constructor, and is curried to b->c->a. The data constructor has three fields, corresponding to the tensor (cartesian) product of three terms in the original definition.

Summary

We have the following layers of abstraction:

V is a monoidal category
A is a tensor category enriched over V
Functors from A to V support a tensor product defined by Day convolution.

Tambara Modules

Modules were defined earlier through the action (left, right, or both) of a tensor category A on some other category X. Tambara modules specialize the category X to the category of distributors D(X, Y). We assume that the categories X and Y are themselves modules over A (that is, they have the action of A defined on them).

We define the left action of A on a distributor (profunctor) L(x, y) as:

a! :: L(x, y) -> L(ax, ay)

Similarly, the right action is given by:

!b :: L(x, y) -> L(xb, yb)

We also assume that the action of the unit object i from A is the identity.

These modules are called, respectively, the left and right Tambara modules. The Tambara (bi-)module supports both left and right actions and is denoted by:

_AD(X, Y)_B

In principle, A may be different from B.

If we choose the tensor product to be the categorical product and replace all categories with one, Tambara modules _AD(A, A)_A become Haskell’s strong profunctors:

class Profunctor p => Strong p where
  first'  :: p a b -> p (a, c) (b, c)
  second' :: p a b -> p (c, a) (c, b)

On the other hand, with the choice of the categorical coproduct as the tensor product, we get choice profunctors:

class Profunctor p => Choice p where
  left'  :: p a b -> p (Either a c) (Either b c)
  right' :: p a b -> p (Either c a) (Either c b)

We can even parameterize these classes by the type of the tensor product:

class (Profunctor p) => TamModule (ten :: * -> * -> *) p where
  leftAction  :: p a b -> p (c `ten` a) (c `ten` b)
  rightAction :: p a b -> p (a `ten` c) (b `ten` c)

and specialize it to:

type TamStrong p = TamModule (,) p
type TamChoice p = TamModule Either p

We can also define a Tambara module as a profunctor with two polymorphic functions:

data TambaraMod (ten :: * -> * -> *) p a b = TambaraMod 
  { runTambaraMod :: (forall c. p (a `ten` c) (b `ten` c),
                      forall d. p (d `ten` a) (d `ten` b))
  }

The Data.Profunctor.Tambara module specializes this definition for product and coproduct tensors. Since both these tensors are symmetric (weakly — up to an isomorphism), they can be constructed with just one polymorphic function each:

newtype Tambara p a b = Tambara { 
    runTambara :: forall c. p (a, c) (b, c) }

newtype TambaraSum p a b = TambaraSum { 
    runTambaraSum :: forall c. p (Either a c) (Either b c) }

Summary

We have the following layers of abstraction:

V is a monoidal category
A (and B) are tensor categories enriched over V
X and Y are categories enriched over V
X is a module if the action of A is defined over X (left, right, or both)
Linear functors between X and Y preserve left, right, or bi actions of A (or B)
A distributor is a functor from X^op × Y to V
Distributors can be composed using coends
Functors from A to V support a tensor product defined by Day convolution
Distributors D(X, Y) form a category enriched over V
Tambara modules are distributors with the action of A (left, right, or bi) defined on them.

Currying Tambara Modules

Let’s look again at the definition of a distributor:

X^op × Y -> V

It’s a functor of two arguments. We know that functions of two arguments can be curried — turned to functions of one argument that return functions. It turns out that a similar thing can be done with distributors. There is an isomorphism between the category of distributors and a category of functors returning functors, which looks very much like currying:

D(X, Y) ≅ Hom(Y, Hom(X^op, V))

According to this isomorphism, a distributor L is mapped to a functor G that takes an object of Y and maps it to another functor that takes an object of X and maps it to an object of V:

L x y = (G y) x

This correspondence may be extended to Tambara modules. Suppose that we have the left action of A defined on X and Y. Then there is an isomorphism of categories:

_AD(X, Y) ≅ Hom_A(Y, Hom(X^op, V))

Remember that the category of left Tambara modules has the left action of A defined by A!. Acting on a distributor L it’s a map:

A! :: L x y -> L (ax) (ay)

On the right hand side of the isomorphism is a category of left-linear functors. An object in this category, K, is left linear:

K (ay) ≅ a(K y)

The target category for this functor is Hom(X^op, V), so K acting on y is another functor that, when acting on an object x of X produces a value in V.

L(x, y) ≅ (K y) x

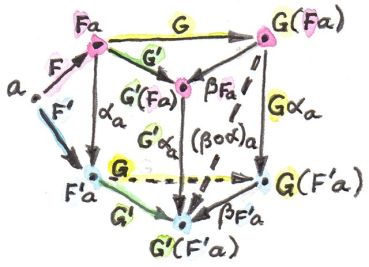
We have to define the action of A! on the right hand side of this isomorphism. First, we use duality (assuming the category is rigid) — the mapping:

η :: i -> a^c a

We get:

(K y) (a^cax)

Now we would like to use left-linearity of Hom(X^op, V) to move the action of a^c out of the functor. Left linear structure on this category is defined by the equation:

(aF) x = F (a^cx)

where F is a functor from X^op to V.

We get:

(K y) (a^cax) = ((aK) y) (ax)

Finally, using left-linearity of K, we can turn this to:

(K (ay)) (ax)

which is what L (ax) (ay) is mapped to.

A similar argument may be used to show the general equivalence of Tambara bimodules with bilinear functors:

_AD(X, Y)_B ≅ Hom_{A, B}(Y, Hom(X^op, V))

Tambara Modules and Centralizers

The “currying” equivalence may be specialized to the case where all four tensor categories are the same:

_AD(A, A)_A ≅ Hom_{A, A}(A, Hom(A^op, V))

Earlier we’ve seen the equivalence of a bilinear functor and a centralizer:

Hom_A,A(A, X) ≅ Z_A(X)

The category X here is an arbitrary tensor category over A. In particular, we can chose X to be Hom(A^op, V). This is the main result in Tambara’s paper:

_AD(A, A)_A ≅ Z_A(Hom(A^op, V))

Earlier we’ve seen that distributors and, in particular, Tambara modules are equipped with a tensor product using Day convolution. Tambara also shows that the centralizers are equipped with a tensor product. The equivalence between Tambara modules and centralizers preserves this tensor product.

Acknowledgments

I’m grateful to Russell O’Connor, Edward Kmett, Dan Doel, Gershom Bazerman, and others, for fruitful discussions and useful comments and to André van Meulebrouck for checking the grammar and spelling.

Next: Free Tambara modules.

November 17, 2015

It’s All About Morphisms

Posted by Bartosz Milewski under Category Theory, Functional Programming, Haskell
[15] Comments

This is part 17 of Categories for Programmers. Previously: Yoneda Embedding. See the Table of Contents.

If I haven’t convinced you yet that category theory is all about morphisms then I haven’t done my job properly. Since the next topic is adjunctions, which are defined in terms of isomorphisms of hom-sets, it makes sense to review our intuitions about the building blocks of hom-sets. Also, you’ll see that adjunctions provide a more general language to describe a lot of constructions we’ve studied before, so it might help to review them too.

Functors

To begin with, you should really think of functors as mappings of morphisms — the view that’s emphasized in the Haskell definition of the Functor typeclass, which revolves around fmap. Of course, functors also map objects — the endpoints of morphisms — otherwise we wouldn’t be able to talk about preserving composition. Objects tell us which pairs of morphisms are composable. The target of one morphism must be equal to the source of the other — if they are to be composed. So if we want the composition of morphisms to be mapped to the composition of lifted morphisms, the mapping of their endpoints is pretty much determined.

Commuting Diagrams

A lot of properties of morphisms are expressed in terms of commuting diagrams. If a particular morphism can be described as a composition of other morphisms in more than one way, then we have a commuting diagram.

In particular, commuting diagrams form the basis of almost all universal constructions (with the notable exceptions of the initial and terminal objects). We’ve seen this in the definitions of products, coproducts, various other (co-)limits, exponential objects, free monoids, etc.

The product is a simple example of a universal construction. We pick two objects a and b and see if there exists an object c, together with a pair of morphisms p and q, that has the universal property of being their product.

A product is a special case of a limit. A limit is defined in terms of cones. A general cone is built from commuting diagrams. Commutativity of those diagrams may be replaced with a suitable naturality condition for the mapping of functors. This way commutativity is reduced to the role of the assembly language for the higher level language of natural transformations.

Natural Transformations

In general, natural transformations are very convenient whenever we need a mapping from morphisms to commuting squares. Two opposing sides of a naturality square are the mappings of some morphism f under two functors F and G. The other sides are the components of the natural transformation (which are also morphisms).

Naturality means that when you move to the “neighboring” component (by neighboring I mean connected by a morphism), you’re not going against the structure of either the category or the functors. It doesn’t matter whether you first use a component of the natural transformation to bridge the gap between objects, and then jump to its neighbor using the functor; or the other way around. The two directions are orthogonal. A natural transformation moves you left and right, and the functors move you up and down or back and forth — so to speak. You can visualize the image of a functor as a sheet in the target category. A natural transformation maps one such sheet corresponding to F, to another, corresponding to G.

We’ve seen examples of this orthogonality in Haskell. There the action of a functor modifies the content of a container without changing its shape, while a natural transformation repackages the untouched contents into a different container. The order of these operations doesn’t matter.

We’ve seen the cones in the definition of a limit replaced by natural transformations. Naturality ensures that the sides of every cone commute. Still, a limit is defined in terms of mappings between cones. These mappings must also satisfy commutativity conditions. (For instance, the triangles in the definition of the product must commute.)

These conditions, too, may be replaced by naturality. You may recall that the universal cone, or the limit, is defined as a natural transformation between the (contravariant) hom-functor:

F :: c -> C(c, Lim D)

and the (also contravariant) functor that maps objects in C to cones, which themselves are natural transformations:

G :: c -> Nat(Δ_c, D)

Here, Δ_c is the constant functor, and D is the functor that defines the diagram in C. Both functors F and G have well defined actions on morphisms in C. It so happens that this particular natural transformation between F and G is an isomorphism.

Natural Isomorphisms

A natural isomorphism — which is a natural transformation whose every component is reversible — is category theory’s way of saying that “two things are the same.” A component of such a transformation must be an isomorphism between objects — a morphism that has the inverse. If you visualize functor images as sheets, a natural isomorphism is a one-to-one invertible mapping between those sheets.

Hom-Sets

But what are morphisms? They do have more structure than objects: unlike objects, morphisms have two ends. But if you fix the source and the target objects, the morphisms between the two form a boring set (at least for locally small categories). We can give elements of this set names like f or g, to distinguish one from another — but what is it, really, that makes them different?

The essential difference between morphisms in a given hom-set lies in the way they compose with other morphisms (from abutting hom-sets). If there is a morphism h whose composition (either pre- or post-) with f is different than that with g, for instance:

h ∘ f ≠ h ∘ g

then we can directly “observe” the difference between f and g. But even if the difference is not directly observable, we might use functors to zoom in on the hom-set. A functor F may map the two morphisms to distinct morphisms:

F f ≠ F g

in a richer category, where the abutting hom-sets provide more resolution, e.g.,

h' ∘ F f ≠ h' ∘ F g

where h' is not in the image of F.

Hom-Set Isomorphisms

A lot of categorical constructions rely on isomorphisms between hom-sets. But since hom-sets are just sets, a plain isomorphism between them doesn’t tell you much. For finite sets, an isomorphism just says that they have the same number of elements. If the sets are infinite, their cardinality must be the same. But any meaningful isomorphism of hom-sets must take into account composition. And composition involves more than one hom-set. We need to define isomorphisms that span whole collections of hom-sets, and we need to impose some compatibility conditions that interoperate with composition. And a natural isomorphism fits the bill exactly.

But what’s a natural isomorphism of hom-sets? Naturality is a property of mappings between functors, not sets. So we are really talking about a natural isomorphism between hom-set-valued functors. These functors are more than just set-valued functors. Their action on morphisms is induced by the appropriate hom-functors. Morphisms are canonically mapped by hom-functors using either pre- or post-composition (depending on the covariance of the functor).

The Yoneda embedding is one example of such an isomorphism. It maps hom-sets in C to hom-sets in the functor category; and it’s natural. One functor in the Yoneda embedding is the hom-functor in C and the other maps objects to sets of natural transformations between hom-sets.

The definition of a limit is also a natural isomorphism between hom-sets (the second one, again, in the functor category):

C(c, Lim D) ≃ Nat(Δ_c, D)

It turns out that our construction of an exponential object, or that of a free monoid, can also be rewritten as a natural isomorphism between hom-sets.

This is no coincidence — we’ll see next that these are just different examples of adjunctions, which are defined as natural isomorphisms of hom-sets.

Asymmetry of Hom-Sets

There is one more observation that will help us understand adjunctions. Hom-sets are, in general, not symmetric. A hom-set C(a, b) is often very different from the hom-set C(b, a). The ultimate demonstration of this asymmetry is a partial order viewed as a category. In a partial order, a morphism from a to b exists if and only if a is less than or equal to b. If a and b are different, then there can be no morphism going the other way, from b to a. So if the hom-set C(a, b) is non-empty, which in this case means it’s a singleton set, then C(b, a) must be empty, unless a = b. The arrows in this category have a definite flow in one direction.

A preorder, which is based on a relation that’s not necessarily antisymmetric, is also “mostly” directional, except for occasional cycles. It’s convenient to think of an arbitrary category as a generalization of a preoder.

A preorder is a thin category — all hom-sets are either singletons or empty. We can visualize a general category as a “thick” preorder.

Challenges

Consider some degenerate cases of a naturality condition and draw the appropriate diagrams. For instance, what happens if either functor F or G map both objects a and b (the ends of f :: a -> b) to the same object, e.g., F a = F b or G a = G b? (Notice that you get a cone or a co-cone this way.) Then consider cases where either F a = G a or F b = G b. Finally, what if you start with a morphism that loops on itself — f :: a -> a?

Next: Adjunctions.

Acknowledgments

I’d like to thank Gershom Bazerman for checking my math and logic, and André van Meulebrouck, who has been volunteering his editing help throughout this series of posts.
Follow @BartoszMilewski

October 28, 2015

Yoneda Embedding

Posted by Bartosz Milewski under Category Theory, Functional Programming, Haskell, Programming
[3] Comments

This is part 16 of Categories for Programmers. Previously: The Yoneda Lemma. See the Table of Contents.

We’ve seen previously that, when we fix an object a in the category C, the mapping C(a, -) is a (covariant) functor from C to Set.

x -> C(a, x)

(The codomain is Set because the hom-set C(a, x) is a set.) We call this mapping a hom-functor — we have previously defined its action on morphisms as well.

Now let’s vary a in this mapping. We get a new mapping that assigns the hom-functor C(a, -) to any a.

a -> C(a, -)

It’s a mapping of objects from category C to functors, which are objects in the functor category (see the section about functor categories in Natural Transformations). Let’s use the notation [C, Set] for the functor category from C to Set. You may also recall that hom-functors are the prototypical representable functors.

Every time we have a mapping of objects between two categories, it’s natural to ask if such a mapping is also a functor. In other words whether we can lift a morphism from one category to a morphism in the other category. A morphism in C is just an element of C(a, b), but a morphism in the functor category [C, Set] is a natural transformation. So we are looking for a mapping of morphisms to natural transformations.

Let’s see if we can find a natural transformation corresponding to a morphism f :: a->b. First, lets see what a and b are mapped to. They are mapped to two functors: C(a, -) and C(b, -). We need a natural transformation between those two functors.

And here’s the trick: we use the Yoneda lemma:

[C, Set](C(a, -), F) ≅ F a

and replace the generic F with the hom-functor C(b, -). We get:

[C, Set](C(a, -), C(b, -)) ≅ C(b, a)

This is exactly the natural transformation between the two hom-functors we were looking for, but with a little twist: We have a mapping between a natural transformation and a morphism — an element of C(b, a) — that goes in the “wrong” direction. But that’s okay; it only means that the functor we are looking at is contravariant.

Actually, we’ve got even more than we bargained for. The mapping from C to [C, Set] is not only a contravariant functor — it is a fully faithful functor. Fullness and faithfulness are properties of functors that describe how they map hom-sets.

A faithful functor is injective on hom-sets, meaning that it maps distinct morphisms to distinct morphisms. In other words, it doesn’t coalesce them.

A full functor is surjective on hom-sets, meaning that it maps one hom-set onto the other hom-set, fully covering the latter.

A fully faithful functor F is a bijection on hom-sets — a one to one matching of all elements of both sets. For every pair of objects a and b in the source category C there is a bijection between C(a, b) and D(F a, F b), where D is the target category of F (in our case, the functor category, [C, Set]). Notice that this doesn’t mean that F is a bijection on objects. There may be objects in D that are not in the image of F, and we can’t say anything about hom-sets for those objects.

The Embedding

The (contravariant) functor we have just described, the functor that maps objects in C to functors in [C, Set]:

a -> C(a, -)

defines the Yoneda embedding. It embeds a category C (strictly speaking, the category C^op, because of contravariance) inside the functor category [C, Set]. It not only maps objects in C to functors, but also faithfully preserves all connections between them.

This is a very useful result because mathematicians know a lot about the category of functors, especially functors whose codomain is Set. We can get a lot of insight about an arbitrary category C by embedding it in the functor category.

Of course there is a dual version of the Yoneda embedding, sometimes called the co-Yoneda embedding. Observe that we could have started by fixing the target object (rather than the source object) of each hom-set, C(-, a). That would give us a contravariant hom-functor. Contravariant functors from C to Set are our familiar presheaves (see, for instance, Limits and Colimits). The co-Yoneda embedding defines the embedding of a category C in the category of presheaves. Its action on morphisms is given by:

[C, Set](C(-, a), C(-, b)) ≅ C(a, b)

Again, mathematicians know a lot about the category of presheaves, so being able to embed an arbitrary category in it is a big win.

Application to Haskell

In Haskell, the Yoneda embedding can be represented as the isomorphism between natural transformations amongst reader functors on the one hand, and functions (going in the opposite direction) on the other hand:

forall x. (a -> x) -> (b -> x) ≅ b -> a

(Remember, the reader functor is equivalent to ((->) a).)

The left hand side of this identity is a polymorphic function that, given a function from a to x and a value of type b, can produce a value of type x (I’m uncurrying — dropping the parentheses around — the function b -> x). The only way this can be done for all x is if our function knows how to convert a b to an a. It has to secretly have access to a function b->a.

Given such a converter, btoa, one can define the left hand side, call itfromY, as:

fromY :: (a -> x) -> b -> x
fromY f b = f (btoa b)

Conversely, given a function fromY we can recover the converter by calling fromY with the identity:

fromY id :: b -> a

This establishes the bijection between functions of the type fromY and btoa.

An alternative way of looking at this isomorphism is that it’s a CPS encoding of a function from b to a. The argument a->x is a continuation (the handler). The result is a function from b to x which, when called with a value of type b, will execute the continuation precomposed with the function being encoded.

The Yoneda embedding also explains some of the alternative representations of data structures in Haskell. In particular, it provides a very useful representation of lenses from the Control.Lens library.

Preorder Example

This example was suggested by Robert Harper. It’s the application of the Yoneda embedding to a category defined by a preorder. A preorder is a set with an ordering relation between its elements that’s traditionally written as <= (less than or equal). The “pre” in preorder is there because we’re only requiring the relation to be transitive and reflexive but not necessarily antisymmetric (so it’s possible to have cycles).

A set with the preorder relation gives rise to a category. The objects are the elements of this set. A morphism from object a to b either doesn’t exist, if the objects cannot be compared or if it’s not true that a <= b; or it exists if a <= b, and it points from a to b. There is never more than one morphism from one object to another. Therefore any hom-set in such a category is either an empty set or a one-element set. Such a category is called thin.

It’s easy to convince yourself that this construction is indeed a category: The arrows are composable because, if a <= b and b <= c then a <= c; and the composition is associative. We also have the identity arrows because every element is (less than or) equal to itself (reflexivity of the underlying relation).

We can now apply the co-Yoneda embedding to a preorder category. In particular, we’re interested in its action on morphisms:

[C, Set](C(-, a), C(-, b)) ≅ C(a, b)

The hom-set on the right hand side is non-empty if and only if a <= b — in which case it’s a one-element set. Consequently, if a <= b, there exists a single natural transformation on the left. Otherwise there is no natural transformation.

So what’s a natural transformation between hom-functors in a preorder? It should be a family of functions between sets C(-, a) and C(-, b). In a preorder, each of these sets can either be empty or a singleton. Let’s see what kind of functions are there at our disposal.

There is a function from an empty set to itself (the identity acting on an empty set), a function absurd from an empty set to a singleton set (it does nothing, since it only needs to be defined for elements of an empty set, of which there are none), and a function from a singleton to itself (the identity acting on a one-element set). The only combination that is forbidden is the mapping from a singleton to an empty set (what would the value of such a function be when acting on the single element?).

So our natural transformation will never connect a singleton hom-set to an empty hom-set. In other words, if x <= a (singleton hom-set C(x, a)) then C(x, b) cannot be empty. A non-empty C(x, b) means that x is less or equal to b. So the existence of the natural transformation in question requires that, for every x, if x <= a then x <= b.

for all x, x ≤ a ⇒ x ≤ b

On the other hand, co-Yoneda tells us that the existence of this natural transformation is equivalent to C(a, b) being non-empty, or to a <= b. Together, we get:

a ≤ b if and only if for all x, x ≤ a ⇒ x ≤ b

We could have arrived at this result directly. The intuition is that, if a <= b then all elements that are below a must also be below b. Conversely, when you substitute a for x on the right hand side, it follows that a <= b. But you must admit that arriving at this result through the Yoneda embedding is much more exciting.

Naturality

The Yoneda lemma establishes the isomorphism between the set of natural transformations and an object in Set. Natural transformations are morphisms in the functor category [C, Set]. The set of natural transformation between any two functors is a hom-set in that category. The Yoneda lemma is the isomorphism:

[C, Set](C(a, -), F) ≅ F a

This isomorphism turns out to be natural in both F and a. In other words, it’s natural in (F, a), a pair taken from the product category [C, Set] × C. Notice that we are now treating F as an object in the functor category.

Let’s think for a moment what this means. A natural isomorphism is an invertible natural transformation between two functors. And indeed, the right hand side of our isomorphism is a functor. It’s a functor from [C, Set] × C to Set. Its action on a pair (F, a) is a set — the result of evaluating the functor F at the object a. This is called the evaluation functor.

The left hand side is also a functor that takes (F, a) to a set of natural transformations [C, Set](C(a, -), F).

To show that these are really functors, we should also define their action on morphisms. But what’s a morphism between a pair (F, a) and (G, b)? It’s a pair of morphisms, (Φ, f); the first being a morphism between functors — a natural transformation — the second being a regular morphism in C.

The evaluation functor takes this pair (Φ, f) and maps it to a function between two sets, F a and G b. We can easily construct such a function from the component of Φ at a (which maps F a to G a) and the morphism f lifted by G:

(G f) ∘ Φ_a

Notice that, because of naturality of Φ, this is the same as:

Φ_b ∘ (F f)

I’m not going to prove the naturality of the whole isomorphism — after you’ve established what the functors are, the proof is pretty mechanical. It follows from the fact that our isomorphism is built up from functors and natural transformations. There is simply no way for it to go wrong.

Challenges

Express the co-Yoneda embedding in Haskell.
Show that the bijection we established between fromY and btoa is an isomorphism (the two mappings are the inverse of each other).
Work out the Yoneda embedding for a monoid. What functor corresponds to the monoid’s single object? What natural transformations correspond to monoid morphisms?
What is the application of the covariant Yoneda embedding to preorders? (Question suggested by Gershom Bazerman.)
Yoneda embedding can be used to embed an arbitrary functor category [C, D] in the functor category [[C, D], Set]. Figure out how it works on morphisms (which in this case are natural transformations).

Next: It’s All About Morphisms.

Acknowledgments

I’d like to thank Gershom Bazerman for checking my math and logic.
Follow @BartoszMilewski

October 7, 2015

Operads, Type Level Nats, and Tic-Tac-Toe

Posted by Bartosz Milewski under Category Theory, Haskell, Programming
[6] Comments

This summer I spent some time talking with Edward Kmett about lots of things. (Which really means that he was talking and I was trying to keep up.) One of the topics was operads. The ideas behind operads are not that hard, if you’ve heard about category theory. But the Haskell wizardry to implement them and their related monads and comonads might be quite challenging. Dan Piponi wrote a blog post about operads and their monads some time ago. He used the operad-based monad to serialize and deserialize tree-like data structures. He showed that those monads may have some practical applications. But what Edward presented me with was an operad-based comonad with no application in sight. And just to make it harder, Edward implemented versions of all those constructs in the context of multicategories, which are operads with typed inputs. Feel free to browse his code on github. In case you feel a little overwhelmed, what follows may provide some guidance.

Let me first introduce some notions so we can start a conversation. You know that in a category you have objects and arrows between them. The usual intuition (at least for a programmer) is that arrows correspond to functions of one argument. To deal with functions of multiple arguments we have to introduce a bit more structure in the category: we need products. A function of multiple arguments may be thought of as a single-argument function taking a product (tuple) of arguments. In a Cartesian closed category, which is what we usually use in programming, we also have exponential objects and currying to represent multi-argument functions. But exponentials are defined in terms of products.

There is an alternative approach: replace single-sourced arrows with multi-sourced ones. An operad is sort of like a category, where morphisms may connect multiple objects to one. So the primitive in an operad is a kind of a tree with multiple inputs and a single output. You can think of it as an n-ary operator. Of course the composition of such primitives is a little tricky — we’ll come back to it later.

Dan Piponi, following Tom Leinster, defined a monad based on an operad. It combines, in one data structure, the tree-like shape with a list of values. You may think of the values as a serialized version of the tree described by the shape. The shapes compose following operad laws. There is another practical application of this data structure: it can be used to represent a decision tree with corresponding probabilities.

But a comonad that Edward implemented was trickier. Instead of containing a list, it produced a list. It was a polymorphic function taking a tree-like shape as an argument and producing a list of results. The original algebraic intuition of an operad representing a family of n-ary operators didn’t really fit this picture. The leaves of the trees corresponded to outputs rather than inputs.

We racked our brains in an attempt to find a problem for which this comonad would be a solution — an activity that is not often acknowledged but probably rather common. We finally came up with an idea of using it to evaluate game trees — and what’s a simpler game than tic-tac-toe? So, taking advantage of the fact that I could ask Edward questions about his multicategory implementation, I set out to writing maybe the most Rube Goldberg-like tic-tac-toe engine in existence.

Here’s the idea: We want to evaluate all possible moves up to a certain depth. We want to find out which ones are illegal (e.g., trying to overwrite a previous move) and which ones are winning; and we’d like to rank the rest. Since there are 9 possible moves at each stage (legal and illegal), we create a tree with the maximum branching factor of 9. The manipulation of such trees follows the laws of an operad.

The comonadic game data structure is the evaluator: given a tree it produces a list of board valuations for each leaf. The game engine picks the best move, and then uses the comonadic duplicate to generate new game states, and so on. This is extremely brute force, but Haskell’s laziness keeps the exponential explosion in check. I added a bit of heuristics to bias the choices towards the center square and the corners, and the program either beats or ties against any player.

All this would be a relatively simple exercise in Haskell programming, so why not make it a little more challenging? The problem involves manipulation of multi-way trees and their matching lists, which is potentially error-prone. When you’re composing operads, you have to precisely match the number of outputs with the number of inputs. Of course, one can have runtime checks and assertions, but that’s not the Haskell way. We want compile-time consistency checks. We need compile-time natural numbers, counted vectors, and counted trees. Needless to say, this makes the code at least an order of magnitude harder to write. There are some libraries, most notably GHC.TypeLits, which help with type literals and simple arithmetic, but I wanted to learn type-level programming the hard way, so I decided not to use them. This is as low level as you can get. In the process I had to rewrite large chunks of the standard Prelude in terms of counted lists and trees. (If you’re interested in the TypeLits version of an operad, I recommend browsing Dan Doel’s code.)

The biggest challenges were related to existential types and to simple arithmetic laws, which we normally take for granted but which have to be explicitly stated when dealing with type-level natural numbers.

Board

The board is a 3 by 3 matrix. A matrix is a vector of vectors. Normally, we would implement vectors as lists and make sure that we never access elements beyond the end of the list. But here we would like to exercise some of the special powers of Haskell and shift bound checking to compile time. So we’ll define a general n by m matrix using counted vectors:

newtype Matrix n m a = Matrix { unMatrix :: Vec n (Vec m a) }

Notice that n and m are types rather than values.

The vector type is parameterized by compile-time natural numbers:

data Vec n a where
    VNil  :: Vec Z a
    VCons :: a -> Vec n a -> Vec (S n) a

This definition is very similar to the definition of a list as a GADT, except that it keeps track of the compile-time size of the vector. So the VNil constructor creates a vector of size Z, which is the compile-time representation of zero. The VCons constructor takes a value of type a and a vector of size n, and produces a vector of size (S n), which stands for the successor of n.

This is how natural numbers may be defined as a data type:

data Nat = Z | S Nat
  deriving Show

Here, Z and S are the two constructors of the data type Nat. But Z and S occur in the definition of Vec as types, not as data constructors. What happens here is that GHC can promote data types to kinds, and data constructors to types. With the extension:

{-# LANGUAGE DataKinds #-}

Nat can double as a kind inhabited by an infinite number of types:

Z, S Z, S (S Z), S (S (S Z)), …

which are in one-to-one correspondence with natural numbers. We can even create type aliases for the first few type naturals:

type One   = S Z
type Two   = S (S Z)
type Three = S (S (S Z))
…

Now the compiler, seeing the use of Z and S in the definition of Vec, can deduce that n is of kind Nat.

The kind Nat is inhabited by types, but these types are not inhabited by values. You cannot create a value of type Z or S Z. So, in data definitions, these types are always phantom types. You don’t pass any values of type Z, S Z, etc., to data constructors. Look at the two Vec constructors: VNil takes no arguments, and VCons takes a value of type a, and a value of type Vec n a.

So far we have encoded the size of the vector into its type, but how do we enforce compile-time bound checking? We do that by providing special access functions. The simplest of them is the vector analog of head:

headV :: Vec (S n) a -> a
headV (VCons a _) = a

The type signature of headV guarantees that it can be called only for vectors of non-zero length (the size has to be the successor of some number n). Notice that this is different from simply not providing a definition for:

headV VNil

An incomplete pattern would result in a runtime error. Here, trying to call headV with VNil produces a compile-time error.

A much more interesting problem is securing safe random access to a vector. A vector of size n can only be indexed by numbers that are strictly less than n. To this end we define, for every n, a separate type for numbers that are less than n

data Fin n where
    FinZ :: Fin (S n) -- zero is less than any successor
    FinS :: Fin n -> Fin (S n) -- n is less than (n+1)

Here, n is a type whose kind is Nat (this can be deduced from the use of S acting on n). Notice that Fin n is a regular inhabited type. In other words its kind is * and you can create values of that type.

Let’s see what the inhabitants of Fin n are. Using the FinZ constructor we can create a value of type Fin (S n), for any n. But Fin (S n) is not a single type — it’s a family of types parameterized by n. FinZ is an example of a polymorphic value. It can be passed to any function that expects Fin One, or Fin Two, etc., but not to one that expects Fin Z.

The FinS constructor takes a value of the type Fin n and produces a value of the type Fin (S n) — the successor of Fin n.

We will use values of the type Fin n to safely index vectors of size n:

ixV :: Fin n -> Vec n a -> a
ixV FinZ (x `VCons` _) = x
ixV (FinS fin_n) (_ `VCons` xs) = ixV fin_n xs

Any attempt at access beyond the end of a vector will result in a compilation error.

In our implementation of the tic-tac-toe board we’ll be using vectors of size Three. It’s easy to enumerate all members of Fin Three. These are:

FinZ             -- zero
FinS FinZ        -- one
FinS (FinS FinZ) -- two

We’ll also need to convert user input to board positions. Of course, not all inputs are valid, so the conversion function will return a Maybe value:

toFin3 :: Int -> Maybe (Fin Three)
toFin3 0 = Just FinZ
toFin3 1 = Just (FinS FinZ)
toFin3 2 = Just (FinS (FinS FinZ))
toFin3 _ = Nothing

Our tic-tac-toe board will be a 3×3 matrix of fields, optionally containing crosses or circles put there by the two players:

data Player = Cross | Circle
  deriving Eq

instance Show Player where
    show Cross  = " X "
    show Circle = " O “

type Board = Matrix Three Three (Maybe Player)

An empty board is filled with Nothing.

Moves

A move in the game consists of a player’s mark and two coordinates. The coordinates are compile-time limited to 0, 1, and 2 using the type Fin Three:

data Move = Move Player (Fin Three) (Fin Three)

The game engine will be dealing with trees of moves. The trees are edge labeled, each edge corresponding to an actual or a potential move. The leaves contain no information, they are just sentinels.

A MoveTree is either a Leaf with a nullary constructor, or a Fan, whose constructor takes Trees n:

data MoveTree n where
    Leaf ::               MoveTree One
    Fan  :: Trees n    -> MoveTree n

Trees is defined as an empty list NilT, or a cons of a branch consisting of a Move and a MoveTree followed by a tail of Trees:

data Trees n where
    NilT ::                                  Trees Z
    (:+) :: (Move, MoveTree k) -> Trees m -> Trees (k + m)

infixr 5 :+

You may recognize this data structure as an edge-labeled version of a rose tree. Here are a few examples of MoveTrees.

t1 :: MoveTree One
t1 = Leaf

t2 :: MoveTree Z
t2 = Fan (NilT)

t3 :: MoveTree One
t3 = Fan $ (Move Cross (FinS FinZ) FinZ, Leaf) :+ NilT

t4 :: MoveTree Two
t4 = Fan $ (Move Circle FinZ FinZ, t3) 
        :+ (Move Circle FinZ (FinS FinZ), t3) 
        :+ NilT

The last tree describes two possible branches: A circle at (0, 0) followed by a cross at (1, 0); and a circle at (0, 1) followed by a cross at (1, 0).

The compile-time parameter n in MoveTree n counts the number of leaves.

Of special interest is the infix constructor (:+) which has to add up the number of leaves in all branches. Here, the addition (k + m) must be performed on types rather than values. To define addition on types we use a multi-parameter type family — type family serving as a compile-time equivalent of a function. Here, the function is an infix operator (+). It takes two types of the kind Nat and produces a type of the kind Nat:

type family (+) (a :: Nat) (b :: Nat) :: Nat

The implementation of this compile-time function is defined inductively through two families of type instances. The base case covers the addition of zero on the left:

type instance Z + m = m

(This is an instance for the type family (+) written in the infix notation.)

The inductive step takes care of adding a successor of n, also on the left:

type instance S n + m = S (n + m)

Notice that the compiler won’t be able to deduce from these definitions that, for instance, m + Z is the same as m. We’ll have to do something special when the need arises — when we are forced to add a zero on the right. Compile-time arithmetic is funny that way.

Operad

The nice thing about move trees is that they are composable. It’s this composability that allows them to be used to speculatively predict multiple futures of a game. Given a current game tree, we can extend it by all possible moves of the computer player, and then extend it by all possible countermoves of the human opponent, and so on. This kind of grafting of trees on top of trees is captured by the operad.

What we are going to do is to consider our move trees as arrows with one or more inputs. Here things might get a little confusing, because a natural interpretation of a move tree is that its input is the first move, the root of the tree; and the leaves are the outputs. But for the sake of the operad, we’ll reverse the meaning of input and output.

In Haskell, we define a category by specifying the hom-set as a type. Then we define the composition of morphisms and pick the identity morphisms. We’ll do a similar thing with the operad. The difference is that an arrow in an operad is parameterized by the number of inputs (leaves of the tree). Continuing with the theme of compile-time safety, we’ll make this parameterization at compile-time.

The analog of the identity arrow will have a single input.

But how do we compose arrows that have multiple inputs? To compose an arrow with n inputs we need something that has n outputs. We can’t get n outputs from a single arrow (for n greater than 1) so we need a whole forest of arrows (with apologies for mixed metaphors). Composition in an operad connects an arrow to a forest. This is the definition:

class (Graded f) => Operad (f :: Nat -> *) where
  ident :: f (S Z)
  compose :: f n -> Forest f m n -> f m

Here, f is a compile-time function from Nat to a regular type — in other words, a data type parameterized by Nat. The identity has one input. Composition takes an n-ary arrow and a forest with m inputs and n outputs. As usual, the obvious identity and associativity laws are assumed but not expressible in Haskell. I’ll define the forest in a moment, but first let’s talk about the additional constraint, Graded f.

Conceptually, a Graded data type provides a way to retrieve its grade — or the count for a counted data structure — at runtime. But why would we need runtime grade information? Wasn’t the whole idea to perform the counting at compile time? It turns out that our compile-time Nats are great at parameterizing data structures. Types of the Nat kind can be used as phantom types. But the same trick won’t work for parameterizing polymorphic functions — there’s no place to insert phantom types into definitions of functions. A function type reflects the types of its arguments and the return type. So if we want to pass a compile-time count to a function, we have to do it through a dummy argument.

For that purpose we need a family of types parameterized by compile-time natural numbers. This time, though, the types must be inhabited, because we need to pass values of those types to functions. These values don’t have to carry any runtime information — they are only used to carry the type. It’s enough that each type be inhabited by a single dummy value, just like it is with the unit type (). Such types are called singleton types. Here’s the definition of the singleton natural number:

data SNat n where
  SZ :: SNat Z
  SS :: SNat n -> SNat (S n)

You can use it to create a series of values:

sZero :: SNat Z
sZero = SZ

sOne :: SNat One
sOne = SS SZ

sTwo :: SNst Two
sTwo = SS (SS SZ)

and so on…

You can also define a function for adding such values. It’s a polymorphic function that takes two singletons and produces another singleton. It really performs addition on types, but it gets the types at compile time from its arguments, and produces a singleton value of the correct type.

plus :: SNat n -> SNat m -> SNat (n + m)
plus SZ n = n
plus (SS n) m = SS (n `plus` m)

The Graded typeclass is defined for counted types — types that are parameterized by Nats:

class Graded (f :: Nat -> *) where
  grade :: f n -> SNat n

Our MoveTrees are easily graded:

instance Graded MoveTree where
    grade Leaf = SS SZ
    grade (Fan ts) = grade ts

instance Graded Trees where
    grade NilT = SZ
    grade ((_, t) :+ ts) = grade t `plus` grade ts

With those preliminaries out of the way, we are ready to implement the Operad instance for the MoveTree. We pick the single leaf tree as our identity.

ident = Leaf

Before we define composition, we have to define a forest. It’s a list of trees parameterized by two compile-time integers, which count the total number of inputs and outputs. A single tree f (our multi-input arrow) is parameterized by the number of inputs. It has the kind Nat->*.

data Forest f n m where
  Nil  :: Forest f Z Z 
  Cons :: f i1 -> Forest f i2 n -> Forest f (i1 + i2) (S n)

The Nil constructor creates an empty forest with zero inputs and zero outputs. The Cons constructor takes a tree with i1 inputs (and, implicitly, one output), and a forest with i2 inputs and n outputs. The result is a forest with i1+i2 inputs and n+1 outputs.

Composition in the operad has the following signature:

compose :: f n -> Forest f m n -> f m

It produces a tree by plugging the outputs of a forest in the inputs of a tree.

We’ll implement composition in multiple stages. First, we make sure that a single leaf is the left identity of our operad. The simplest case is when the right operand is a single-leaf forest :

compose Leaf (Cons Leaf Nil) = Leaf

A little complication arises when we want to compose the identity with a single-tree forest. Naively, we would like to write:

compose Leaf (Cons t Nil) = t

This should work, since the leaf has one input, and the single-tree forest has one output. Looking at the signature of compose, the compiler should be able to deduce that n in the definition of compose should be replaced by S Z. Let’s follow the arithmetic.

The forest is the result of Consing a tree with i1 inputs, and a Nil forest with Z inputs and Z outputs. By definition of Cons, the resulting forest has i1+Z inputs and S Z outputs. So the ns in compose match. The problem is with unifying the ms. The one from the forest is equal to i1+Z, and the one on the right hand side is i1. And herein lies the trouble: we are adding Z on the right of i1. As I mentioned before, the compiler has no idea that i1+Z is the same as i1. We’re stuck! The solution to this problem requires some cheating, as well as digging into the brave new world of constraint kinds.

Constraint Kinds

We want to tell the compiler that two types, n and (n + Z) are the same. Both types are of the kind Nat. Equality of types can be expressed as a constraint with the tilde between the two types:

n ~ (n + Z)

Constraints are inhabitants of a special kind called Constraint. Besides type equality, they can express typeclass constraints like Eq or Num.

The compiler treats constraints as if they were types and, in fact, lets you define type aliases for them:

type Stringy a = (Show a, Read a)

Here, Stringy, just like Show and Read, is of the kind * -> Constraint. Unlike regular types of kind *, constraints are not inhabited by values. You can use them as contexts in front of the double arrow, =>, but you can’t pass them as runtime values.

This situation is very similar to what we’ve seen with the Nat kind, which also contained uninhabited types. But with Nat we were able to reify those types by defining the corresponding singletons. A very similar trick works with Constraints. A reified constraint singleton is called a Dict:

data Dict :: Constraint -> * where
  Dict :: a => Dict a

In particular, if a is a typeclass constraint, you can think of Dict as a class dictionary — the generalization of a virtual table. There is in fact a hidden singleton that is passed by the compiler to functions with typeclass constraints. For instance, the function:

print :: Show a => a -> IO ()

is translated to a function of two variables, one of them being the virtual table for the typeclass Show. When you call print with an Int, the compiler finds the virtual table for the Show instance of Int and passes it to print.

The difference is that now we are trying to do explicitly what the compiler normally hides from us.

Notice that Dict has only one constructor that takes no arguments. You can construct a Dict from thin air. But because it’s a polymorphic value, you either have to specify what type of Dict you want to construct, or give the compiler enough information to figure it out on its own.

How do you specify the concrete type of a Dict? Dict is a type constructor of the kind Constraint->* so, to define a specific type, you need to provide a constraint. For instance, you could construct a dictionary using the constraint that the type One is the same as the type (One + Z):

myDict :: Dict (One ~ (One + Z))
myDict = Dict

This actually works, but it doesn’t generalize. What we really need is a whole family of singletons parameterized by n:

plusZ :: forall n. Dict (n ~ (n + Z))

But the compiler is not able to verify an infinite family of constraints. We are stuck!

When everything else fails, try cheating. Cheating in Haskell is called unsafeCoerce. We can take a dictionary that we know exists, for instance that of (n ~ n) and force the compiler to believe that it’s the right type:

plusZ :: forall n. Dict (n ~ (n + Z))
plusZ = unsafeCoerce (Dict :: Dict (n ~ n))

This is to be expected: We are hitting the limits of Haskell. Haskell is not a dependent type language and it’s not a theorem prover. It’s possible to avoid some of the ugliness by using TypeLits, but I wanted to show you the low level details.

To truly understand the meaning of constraints, we should take a moment to talk about the Curry-Howard isomorphism. It tells us that types are equivalent to propositions: logical statement that can be either true or false. A type that is inhabited corresponds to a true statement. Most data types we define in a program are clearly inhabited. They have constructors that let us create values — the inhabitants of a given type. Then there are function types, which may or may not be inhabited. If you can implement a function of a given type, then you have a proof that this type is inhabited. Things get really interesting when you consider polymorphic functions. They correspond to propositions with quantifiers. We know, for instance, that the type a->a is inhabited for all a — we have the proof: the identity function.

A type like Dict is even more interesting. It explicitly specifies the condition under which it is inhabited. The type Dict a is inhabited if the constraint a is true. For instance, (n ~ n) is true, so the corresponding dictionary, Dict (n ~ n), can be constructed. What’s even more interesting is that, if you can hand the compiler an instance of a particular dictionary, it is proof enough that the constraint it encapsulates is true. The actual value of plusZ is irrelevant but its existence is critical.

So how do we bring it to the compiler’s attention? One way is to pass the dictionary as an argument to a function, but that’s awkward. In our case, the signature of the function compose is fixed. A better option is to bring a proof to the local scope by pattern matching.

compose Leaf (Cons (t :: MoveTree m) Nil) = 
    case plusZ :: Dict (m ~ (m + Z)) of Dict -> t

Notice how we first introduce m into the scope by explicitly typing t inside the pattern for Forest. We fix the type of t to be:

MoveTree m

Then we explicitly type the value of plusZ, our global singleton, to be:

Dict (m ~ (m + Z))

This lets the compiler unify the n in the original definition of plusZ with our local m. Finally we pattern-match plusZ to its constructor, Dict. Obviously, the match will succeed. We don’t care about the result of this match, except that it introduces the proof of (m ~ (m + Z)) into the inner scope. It will let the compiler complete the type checking by unifying the actual type of t with the expected return type of compose.

Splitting the Forest

So far we have dealt with the simple cases of operadic composition, the ones where the left hand side had just one input. The general case involves connecting a tree that has k inputs to a forest that has k outputs and an arbitrary number of inputs. A MoveTree that is not a single Leaf is a Fan of Trees, which can be further split into the head tree and the tail. This corresponds to the pattern:

compose (Fan ((mv, t) :+ ts)) frt

We will proceed by recursion. The base case is the empty Fan:

compose (Fan NilT) Nil = Fan NilT

In the recursive case we have to split the forest frt into the part that matches the inputs of the tree t, and the remainder. The number of inputs of t is given by its grade — that’s why we needed the operad to be Graded.

If Forest was a simple list of trees, splitting it would be trivial: there’s even a function called splitAt in the Prelude. The fact that a Forest is counted makes it more interesting. But the real problem is that a Forest is parameterized by both the number of inputs and outputs. We want to separate a certain number of outputs, say m, but we have no idea how many inputs, i1, will go with that number of outputs. It depends on how much the individual trees branch inside the forest.

To see the problem, let’s try to come up with a signature for splitForest. It should look something like this:

splitForest :: SNat m -> SNat n -> Forest f i (m + n) 
    -> (Forest f i1 m, Forest f i2 n)

But what are i1 and i2? All we know is that they exist and that they should add up to i. If there was an existential quantifier in Haskell, we could try writing something like this:

splitForest :: exists i1 i2. (i1 + i2 ~ i) => 
    SNat m -> SNat n -> Forest f i (m + n)
    -> (Forest f i1 m, Forest f i2 n)

We can’t do exactly that, but this pseudocode suggests a neat workaround. The existential quantifier may be replaced by a universal quantifier under a CPS transformation. There is a Curry-Howard reason for that, which has to do with CPS representing logical negation. But this can also be easily explained programmatically. Since we cannot predict how the inputs will split in the general case; instead of returning a concrete result we may ask the caller to provide a function — a continuation — that can accept an arbitrary split and take over from there. The continuation itself must be universally quantified: it must work for all splits. Here’s the signature of the continuation:

(forall i1 i2. (i ~ (i1 + i2)) => 
        (Forest f i1 m, Forest f i2 n) -> r)

As usual, when doing a CPS transform we don’t care what the type r is — in fact, we have to universally quantify over it. And since we have a local constraint that involves i, we have to bring i into the inner scope. The way to scope type variables in Haskell is to explicitly quantify over them. And once you quantify over one type variable, you have to quantify over all of them. That’s why the declaration of splitForest starts with one giant quantifier:

forall m n i f r

Putting it all together, here’s the final type signature of splitForest:

splitForest :: forall m n i f r. SNat m -> SNat n -> Forest f i (m+n)
    -> (forall i1 i2. (i ~ (i1 + i2)) => 
        (Forest f i1 m, Forest f i2 n) -> r) 
    -> r

We will implement splitForest using recursion. The base case splits the forest at offset zero. It simply calls the continuation k with a pair consisting of an empty fragment and the unchanged forest:

splitForest SZ _ fs k = k (Nil, fs)

The recursive case is conceptually simple. The offset at which you split the forest is the successor of some number represented by a singleton sm. The forest itself is a Cons of a tree t and some tail ts. We want to split this tail into two fragments at sm — one less than (SS sm). We return the pair whose first component is the Cons of the tree t and the first fragment, and whose second component is the second fragment. Except that, instead of returning, we call the continuation. And in order to split the tail, we have to create another continuation to accept the fragments. So here’s the skeleton of the implementation:

splitForest (SS sm) 
            sn 
            (Cons t ts) 
            k =
    splitForest sm sn ts $
        ((m_frag, n_frag) -> k (Cons t m_frag, n_frag)

To make this compile, we need to fill in some of the type signatures. In particular, we need to extract the number of inputs i1 and i2 from the constituents of the forest. We also have to extract the number of inputs i3 and i4 of the fragments. Finally, we have to tell the compiler that addition is associative. I won’t go into the gory details, I’ll just show you the final implementation:

splitForest (SS (sm :: SNat m_1)) 
            sn 
            (Cons (t :: f i1) (ts :: Forest f i2 (m_1 + n))) 
            k =
    splitForest sm sn ts $
        ((m_frag :: Forest f i3 m_1), (n_frag :: Forest f i4 n)) ->
            case plusAssoc (Proxy :: Proxy i1) 
                           (Proxy :: Proxy i3) 
                           (Proxy :: Proxy i4) of 
               Dict -> k (Cons t m_frag, n_frag)

But what’s this Proxy business? The compiler is having — again — a problem with simple arithmetic. This time it’s the associativity of addition. We have to provide a proof that:

((i1 + i3) + i4) ~ (i1 + (i3 + i4))

But this time we can’t fake it with a polymorphic value; like we did with plusZ, which was parameterized by a single type of the kind Nat. We have to fake it with a polymorphic function:

plusAssoc :: p a -> q b -> r c -> Dict (((a + b) + c) ~ (a + (b + c)))
plusAssoc _ _ _ = unsafeCoerce (Dict :: Dict (a ~ a))

Here p, q, and r, are some arbitrary type constructors of the kind Nat->*. It doesn’t matter what the values of the arguements are, as long as they introduce the three (uninhabited) types, a, b, and c, into the scope. Proxy is a very simple polymorphic singleton type:

data Proxy t = Proxy

We create three Proxy values and call the function plusAssoc, which returns a dictionary that witnesses the associativity of the addition of the three Nats.

Equipped with the function splitForest, we can now complete our Operad instance:

instance Operad MoveTree where
    ident = Leaf
    compose Leaf (Cons Leaf Nil) = Leaf
    compose Leaf (Cons (t :: MoveTree m) Nil) = 
        case plusZ :: Dict (m ~ (m + Z)) of Dict -> t
    compose (Fan NilT) Nil = Fan NilT
    compose (Fan ((mv, t) :+ ts)) frt = 
        Fan $ splitForest (grade t) (grade ts) frt $
              (mts1, mts2) ->
                 let tree  = (compose t mts1)
                     (Fan trees) = (compose (Fan ts) mts2)
                 in (mv, tree) :+ trees
    compose _ _ = error "compose!"

The Comonad

A comonad is the dual of a monad. Just like a monad lets you lift a value using return, a comonad lets you extract a value. And just like a monad lets you collapse double encapsulation to single encapsulation using join, a comonad lets you duplicate the encapsulation.

class Functor w => Comonad w where
   extract :: w a -> a
   duplicate :: w a -> w (w a)

In other words, a monad lets you put stuff in and reduce whereas a comonad lets you take stuff out and reproduce.

A list monad, for instance, implements return by constructing a singleton list, and join by concatenating a list of lists.

An infinite list, or a stream comonad, implements extract by accessing the head of the list and duplicate by creating a stream of consecutive tails.

An operad can be used to define both a monad and a comonad. The monad M combines an operadic tree of n inputs with a vector of n elements.

data M f a where
   M :: f n -> Vec n a -> M f a

Monadic return combines the operadic identity with a singleton vector, whereas join grafts the operadic trees stored in the vector into the operad using compose and then concatenates the vectors.

The comonad W is also pretty straightforward. It’s defined as a polymorphic function, the evaluator, that takes an operad f n and produces a vector Vec n:

newtype W f a = W { runW :: forall n. f n -> Vec n a }

It’s obviously a functor:

instance Functor (W f) where
    fmap g (W k) = W $ f -> fmap g (k f)

Comonadic extract calls the evaluator with the identity operad and extracts the value from the singleton vector:

extract (W k) = case k ident of
    VCons a VNil -> a

The implementation of duplicate is a bit more involved. Its signature is:

duplicate :: W f -> W (W f)

Given the evaluator inside W f:

ev :: forall n. f n -> Vec n a

it has to produce another evaluator:

forall m. f m -> Vec m (W f)

This function, when called with an operadic tree f m, which I’ll call the outer tree, must produce m new evaluators.

What should the kth such evaluator do when called with the inner tree fi? The obvious thing is to graft the inner tree at the kth input of the outer tree. We can saturate the rest of the inputs of the outer tree with identities. Then we’ll call the evaluator ev with this new larger tree to get a larger vector. Our desired result will be in the middle of this vector at offset k.

This is the complete implementation of the comonad:

instance Operad f => Comonad (W f) where
  extract (W k) = case k ident of
    VCons a VNil -> a
  duplicate (W ev :: W f a) = W $ f -> go f SZ (grade f)
    where
      -- n increases, m decreases
      -- n starts at zero, m starts at (grade f)
      go :: f (n + m) -> SNat n -> SNat m -> Vec m (W f a)
      go _ _ SZ = VNil
      go f n (SS m) =  case succAssoc n m of 
          Dict -> W ev' `VCons` go f (SS n) m
        where
          ev' :: f k -> Vec k a
          ev' fk = middleV n (grade fk) m 
                           (ev (f `compose` plantTreeAt n m fk))

As usual, we had to help the compiler with the arithmetic. This time it was the associativity of the successor:

succAssoc :: p a -> q b -> Dict ((a + S b) ~ S (a + b))
succAssoc _ _ = unsafeCoerce (Dict :: Dict (a ~ a))

Notice that we didn’t have to use the Proxy trick in succAssoc n m, since we had the singletons handy.

The Tic Tac Toe Comonad

The W comonad works with any operad, in particular it will work with our MoveTree.

type TicTacToe = W MoveTree Evaluation

We want the evaluator for this comonad to produce a vector of Evaluations, which we will define as:

type Evaluation = (Score, MoveTree One)

The scoring is done from the perspective of the computer. A Bad move is a move that falls on an already marked square. A Good move carries with it an integer score:

data Score = Bad | Win | Lose | Good Int
  deriving (Show, Eq)

Evaluation includes a single-branch MoveTree One, which is the list of moves that led to this evaluation. In particular, the singleton Evaluation returned by extract will contain the history of moves up to the current point in the game.

Let’s see what duplicate does in our case. It produces a vector of TicTacToe games, each containing a new evaluator. These new evaluators, when called with a move tree, whether it’s a single move, a tree of 9 possible moves, a tree of 81 possible moves and responses, etc.; will graft this tree to the corresponding leaf of the previous game tree and perform the evaluation. We’ll call duplicate after every move and pick one of the resulting games (evaluators).

The Evaluator

This blog post is mostly about operads and comonads, so I won’t go into a lot of detail about implementing game strategy. I’ll just give a general overview, and if you’re curious, you can view the code on github.

The heart of the operadic comonad is the evaluator function. To start the whole process running, we’ll create the initial board. We’ll use the function eval that takes a board and returns an evaluator (which is eval partially applied to the board).

main :: IO ()
main = do
    putStrLn "Make your moves by entering x y coordinates 1..3 1..3."
    let board = emptyBoard
        game = W (eval board)
    play board game

The evaluator is a function that takes a MoveTree and returns a vector of Evaluation. If the tree is just a single leaf (that’s the identity of our operad), the evaluation is trivial. The interesting part is the evaluation of a Fan of branches.

eval :: Board -> MoveTree n -> Vec n Evaluation
eval board moves = case moves of
    Leaf   -> singleV (Good 0, Leaf)
    Fan ts -> evalTs (evalBranch board) ts

The function evalTs iterates over branches, applying a branch evaluator to each tree and concatenating the resulting evaluation vectors. The only tricky part is that each branch may end in a different number of leaves, so the branch evaluator must be polymorphic in k:

evalTs :: (forall k. (Move, MoveTree k) -> Vec k Evaluation) 
          -> Trees n 
          -> Vec n Evaluation
evalTs _ NilT = VNil
evalTs ev (br :+ ts) = concatV (ev br) (evalTs f ts)

The branch evaluator must account for the possibility that a move might be invalid — it has to test whether the square has already been marked on the board. If it’s not, it marks the board and evaluates the move.

First, there are two simple cases: the move could be a winning move or a losing move. In those cases when the result is known immediately, that is Bad, Win, or Lose, evalBranch returns a vector of the size determined by the number of leaves in the branch. The vector is filled with the appropriate values (Bad, Win, or Lose).

The interesting case is when the move is neither invalid nor decisive. In that case we recurse into eval with the new board and the sub-tree that follows the move in question. We gather the resulting evaluations and adjust the scores. If any of the branches results in a loss, we lower the score on all of them. Otherwise we add the score of the current move to all scores for that tree.

Game Logic

At the very top level we have the game loop, which takes input from the user and responds with the computer’s move. A user move must be tested for correctness. First it’s converted to two Fin Three values (or Nothing). Then we create a singleton MoveTree with that move and pass it to the evaluator. If the move is invalid, we continue prompting the user. If the move is decisive, we announce the winner. Otherwise, we advance the game by calling duplicate, and then pick the new evaluator from the resulting tree of comonadic values — the one corresponding to the user move.

To generate the computer response, we create a two-deep tree of all possible moves (that is one computer move and one user move — that seems to be enough of the depth to win or tie every time). We call the evaluator with that tree and pick the best result. Again, if it’s a decisive move, we announce the winner. Otherwise, we call duplicate again, and pick the new evaluator corresponding to the selected move.

Conclusion

Does it make sense to implement tic-tac-toe using such heavy machinery? Not really! But it makes sense as an exercise in compile-time safety guarantees. I wouldn’t mind if those techniques were applied to writing software that makes life-and-death decisions. Nuclear reactors, killer drones, or airplane auto-pilots come to mind. Fast stock-trading software, even though it cannot kill you directly, can also be mission critical, if you’re attached to your billions. What’s an overkill in one situation may save your life in another. You need different tools for different tasks and Haskell provides the options.

The full source is available on github.

Thanks go to André van Meulebrouck for his editing help.

September 1, 2015

The Yoneda Lemma

Posted by Bartosz Milewski under Category Theory, Haskell, Programming
[27] Comments

This is part 15 of Categories for Programmers. Previously: Representable Functors. See the Table of Contents.

Most constructions in category theory are generalizations of results from other more specific areas of mathematics. Things like products, coproducts, monoids, exponentials, etc., have been known long before category theory. They might have been known under different names in different branches of mathematics. A cartesian product in set theory, a meet in order theory, a conjunction in logic — they are all specific examples of the abstract idea of a categorical product.

The Yoneda lemma stands out in this respect as a sweeping statement about categories in general with little or no precedent in other branches of mathematics. Some say that its closest analog is Cayley’s theorem in group theory (every group is isomorphic to a permutation group of some set).

The setting for the Yoneda lemma is an arbitrary category C together with a functor F from C to Set. We’ve seen in the previous section that some Set-valued functors are representable, that is isomorphic to a hom-functor. The Yoneda lemma tells us that all Set-valued functors can be obtained from hom-functors through natural transformations, and it explicitly enumerates all such transformations.

When I talked about natural transformations, I mentioned that the naturality condition can be quite restrictive. When you define a component of a natural transformation at one object, naturality may be strong enough to “transport” this component to another object that is connected to it through a morphism. The more arrows between objects in the source and the target categories there are, the more constraints you have for transporting the components of natural transformations. Set happens to be a very arrow-rich category.

The Yoneda lemma tells us that a natural transformation between a hom-functor and any other functor F is completely determined by specifying the value of its single component at just one point! The rest of the natural transformation just follows from naturality conditions.

So let’s review the naturality condition between the two functors involved in the Yoneda lemma. The first functor is the hom-functor. It maps any object x in C to the set of morphisms C(a, x) — for a a fixed object in C. We’ve also seen that it maps any morphism f from x to y to C(a, f).

The second functor is an arbitrary Set-valued functor F.

Let’s call the natural transformation between these two functors α. Because we are operating in Set, the components of the natural transformation, like α_x or α_y, are just regular functions between sets:

α_x :: C(a, x) -> F x
α_y :: C(a, y) -> F y

And because these are just functions, we can look at their values at specific points. But what’s a point in the set C(a, x)? Here’s the key observation: Every point in the set C(a, x) is also a morphism h from a to x.

So the naturality square for α:

α_y ∘ C(a, f) = F f ∘ α_x

becomes, point-wise, when acting on h:

α_y (C(a, f) h) = (F f) (α_x h)

You might recall from the previous section that the action of the hom-functor C(a,-) on a morphism f was defined as precomposition:

C(a, f) h = f ∘ h

which leads to:

α_y (f ∘ h) = (F f) (α_x h)

Just how strong this condition is can be seen by specializing it to the case of x equal to a.

In that case h becomes a morphism from a to a. We know that there is at least one such morphism, h = id_a. Let’s plug it in:

α_y f = (F f) (α_a id_a)

Notice what has just happened: The left hand side is the action of α_y on an arbitrary element f of C(a, y). And it is totally determined by the single value of α_a at id_a. We can pick any such value and it will generate a natural transformation. Since the values of α_a are in the set F a, any point in F a will define some α.

Conversely, given any natural transformation α from C(a, -) to F, you can evaluate it at id_a to get a point in F a.

We have just proven the Yoneda lemma:

There is a one-to-one correspondence between natural transformations from C(a, -) to F and elements of F a.

in other words,

Nat(C(a, -), F) ≅ F a

Or, if we use the notation [C, Set] for the functor category between C and Set, the set of natural transformation is just a hom-set in that category, and we can write:

[C, Set](C(a, -), F) ≅ F a

I’ll explain later how this correspondence is in fact a natural isomorphism.

Now let’s try to get some intuition about this result. The most amazing thing is that the whole natural transformation crystallizes from just one nucleation site: the value we assign to it at id_a. It spreads from that point following the naturality condition. It floods the image of C in Set. So let’s first consider what the image of C is under C(a, -).

Let’s start with the image of a itself. Under the hom-functor C(a, -), a is mapped to the set C(a, a). Under the functor F, on the other hand, it is mapped to the set F a. The component of the natural transformation α_a is some function from C(a, a) to F a. Let’s focus on just one point in the set C(a, a), the point corresponding to the morphism id_a. To emphasize the fact that it’s just a point in a set, let’s call it p. The component α_a should map p to some point q in F a. I’ll show you that any choice of q leads to a unique natural transformation.

The first claim is that the choice of one point q uniquely determines the rest of the function α_a. Indeed, let’s pick any other point, p' in C(a, a), corresponding to some morphism g from a to a. And here’s where the magic of the Yoneda lemma happens: g can be viewed as a point p' in the set C(a, a). At the same time, it selects two functions between sets. Indeed, under the hom-functor, the morphism g is mapped to a function C(a, g); and under F it’s mapped to F g.

Now let’s consider the action of C(a, g) on our original p which, as you remember, corresponds to id_a. It is defined as precomposition, g∘id_a, which is equal to g, which corresponds to our point p'. So the morphism g is mapped to a function that, when acting on p produces p', which is g. We have come full circle!

Now consider the action of F g on q. It is some q', a point in F a. To complete the naturality square, p' must be mapped to q' under α_a. We picked an arbitrary p' (an arbitrary g) and derived its mapping under α_a. The function α_a is thus completely determined.

The second claim is that α_x is uniquely determined for any object x in C that is connected to a. The reasoning is analogous, except that now we have two more sets, C(a, x) and F x, and the morphism g from a to x is mapped, under the hom-functor, to:

C(a, g) :: C(a, a) -> C(a, x)

and under F to:

F g :: F a -> F x

Again, C(a, g) acting on our p is given by the precomposition: g ∘ id_a, which corresponds to a point p' in C(a, x). Naturality determines the value of α_x acting on p' to be:

q' = (F g) q

Since p' was arbitrary, the whole function α_x is thus determined.

What if there are objects in C that have no connection to a? They are all mapped under C(a, -) to a single set — the empty set. Recall that the empty set is the initial object in the category of sets. It means that there is a unique function from this set to any other set. We called this function absurd. So here, again, we have no choice for the component of the natural transformation: it can only be absurd.

One way of understanding the Yoneda lemma is to realize that natural transformations between Set-valued functors are just families of functions, and functions are in general lossy. A function may collapse information and it may cover only parts of its codomain. The only functions that are not lossy are the ones that are invertible — the isomorphisms. It follows then that the best structure-preserving Set-valued functors are the representable ones. They are either the hom-functors or the functors that are naturally isomorphic to hom-functors. Any other functor F is obtained from a hom-functor through a lossy transformation. Such a transformation may not only lose information, but it may also cover only a small part of the image of the functor F in Set.

Yoneda in Haskell

We have already encountered the hom-functor in Haskell under the guise of the reader functor:

type Reader a x = a -> x

The reader maps morphisms (here, functions) by precomposition:

instance Functor (Reader a) where
    fmap f h = f . h

The Yoneda lemma tells us that the reader functor can be naturally mapped to any other functor.

A natural transformation is a polymorphic function. So given a functor F, we have a mapping to it from the reader functor:

alpha :: forall x . (a -> x) -> F x

As usual, forall is optional, but I like to write it explicitly to emphasize parametric polymorphism of natural transformations.

The Yoneda lemma tells us that these natural transformations are in one-to-one correspondence with the elements of F a:

forall x . (a -> x) -> F x ≅ F a

The right hand side of this identity is what we would normally consider a data structure. Remember the interpretation of functors as generalized containers? F a is a container of a. But the left hand side is a polymorphic function that takes a function as an argument. The Yoneda lemma tells us that the two representations are equivalent — they contain the same information.

Another way of saying this is: Give me a polymorphic function of the type:

alpha :: forall x . (a -> x) -> F x

and I’ll produce a container of a. The trick is the one we used in the proof of the Yoneda lemma: we call this function with id to get an element of F a:

alpha id :: F a

The converse is also true: Given a value of the type F a:

fa :: F a

one can define a polymorphic function:

alpha h = fmap h fa

of the correct type. You can easily go back and forth between the two representations.

The advantage of having multiple representations is that one might be easier to compose than the other, or that one might be more efficient in some applications than the other.

The simplest illustration of this principle is the code transformation that is often used in compiler construction: the continuation passing style or CPS. It’s the simplest application of the Yoneda lemma to the identity functor. Replacing F with identity produces:

forall r . (a -> r) -> r ≅ a

The interpretation of this formula is that any type a can be replaced by a function that takes a “handler” for a. A handler is a function accepting a and performing the rest of the computation — the continuation. (The type r usually encapsulates some kind of status code.)

This style of programming is very common in UIs, in asynchronous systems, and in concurrent programming. The drawback of CPS is that it involves inversion of control. The code is split between producers and consumers (handlers), and is not easily composable. Anybody who’s done any amount of nontrivial web programming is familiar with the nightmare of spaghetti code from interacting stateful handlers. As we’ll see later, judicious use of functors and monads can restore some compositional properties of CPS.

Co-Yoneda

As usual, we get a bonus construction by inverting the direction of arrows. The Yoneda lemma can be applied to the opposite category C^op to give us a mapping between contravariant functors.

Equivalently, we can derive the co-Yoneda lemma by fixing the target object of our hom-functors instead of the source. We get the contravariant hom-functor from C to Set: C(-, a). The contravariant version of the Yoneda lemma establishes one-to-one correspondence between natural transformations from this functor to any other contravariant functor F and the elements of the set F a:

Nat(C(-, a), F) ≅ F a

Here’s the Haskell version of the co-Yoneda lemma:

forall x . (x -> a) -> F x ≅ F a

Notice that in some literature it’s the contravariant version that’s called the Yoneda lemma.

Challenges

Show that the two functions phi and psi that form the Yoneda isomorphism in Haskell are inverses of each other.

phi :: (forall x . (a -> x) -> F x) -> F a
phi alpha = alpha id

psi :: F a -> (forall x . (a -> x) -> F x)
psi fa h = fmap h fa

A discrete category is one that has objects but no morphisms other than identity morphisms. How does the Yoneda lemma work for functors from such a category?
A list of units [()] contains no other information but its length. So, as a data type, it can be considered an encoding of integers. An empty list encodes zero, a singleton [()] (a value, not a type) encodes one, and so on. Construct another representation of this data type using the Yoneda lemma for the list functor.

Bibliography

Catsters video

Next: Yoneda Embedding.

Acknowledgments

I’d like to thank Gershom Bazerman for checking my math and logic, and André van Meulebrouck, who has been volunteering his editing help throughout this series of posts.
Follow @BartoszMilewski

July 21, 2015

Free Monoids

Posted by Bartosz Milewski under Category Theory, Functional Programming, Haskell, Programming
[33] Comments

This is part 13 of Categories for Programmers. Previously: Limits and Colimits. See the Table of Contents.

Monoids are an important concept in both category theory and in programming. Categories correspond to strongly typed languages, monoids to untyped languages. That’s because in a monoid you can compose any two arrows, just as in an untyped language you can compose any two functions (of course, you may end up with a runtime error when you execute your program).

We’ve seen that a monoid may be described as a category with a single object, where all logic is encoded in the rules of morphism composition. This categorical model is fully equivalent to the more traditional set-theoretical definition of a monoid, where we “multiply” two elements of a set to get a third element. This process of “multiplication” can be further dissected into first forming a pair of elements and then identifying this pair with an existing element — their “product.”

What happens when we forgo the second part of multiplication — the identification of pairs with existing elements? We can, for instance, start with an arbitrary set, form all possible pairs of elements, and call them new elements. Then we’ll pair these new elements with all possible elements, and so on. This is a chain reaction — we’ll keep adding new elements forever. The result, an infinite set, will be almost a monoid. But a monoid also needs a unit element and the law of associativity. No problem, we can add a special unit element and identify some of the pairs — just enough to support the unit and associativity laws.

Let’s see how this works in a simple example. Let’s start with a set of two elements, {a, b}. We’ll call them the generators of the free monoid. First, we’ll add a special element e to serve as the unit. Next we’ll add all the pairs of elements and call them “products”. The product of a and b will be the pair (a, b). The product of b and a will be the pair (b, a), the product of a with a will be (a, a), the product of b with b will be (b, b). We can also form pairs with e, like (a, e), (e, b), etc., but we’ll identify them with a, b, etc. So in this round we’ll only add (a, a), (a, b) and (b, a) and (b, b), and end up with the set {e, a, b, (a, a), (a, b), (b, a), (b, b)}.

In the next round we’ll keep adding elements like: (a, (a, b)), ((a, b), a), etc. At this point we’ll have to make sure that associativity holds, so we’ll identify (a, (b, a)) with ((a, b), a), etc. In other words, we won’t be needing internal parentheses.

You can guess what the final result of this process will be: we’ll create all possible lists of as and bs. In fact, if we represent e as an empty list, we can see that our “multiplication” is nothing but list concatenation.

This kind of construction, in which you keep generating all possible combinations of elements, and perform the minimum number of identifications — just enough to uphold the laws — is called a free construction. What we have just done is to construct a free monoid from the set of generators {a, b}.

Free Monoid in Haskell

A two-element set in Haskell is equivalent to the type Bool, and the free monoid generated by this set is equivalent to the type [Bool] (list of Bool). (I am deliberately ignoring problems with infinite lists.)

A monoid in Haskell is defined by the type class:

class Monoid m where
    mempty  :: m
    mappend :: m -> m -> m

This just says that every Monoid must have a neutral element, which is called mempty, and a binary function (multiplication) called mappend. The unit and associativity laws cannot be expressed in Haskell and must be verified by the programmer every time a monoid is instantiated.

The fact that a list of any type forms a monoid is described by this instance definition:

instance Monoid [a] where
    mempty  = []
    mappend = (++)

It states that an empty list [] is the unit element, and list concatenation (++) is the binary operation.

As we have seen, a list of type a corresponds to a free monoid with the set a serving as generators. The set of natural numbers with multiplication is not a free monoid, because we identify lots of products. Compare for instance:

2 * 3 = 6
[2] ++ [3] = [2, 3] // not the same as [6]

That was easy, but the question is, can we perform this free construction in category theory, where we are not allowed to look inside objects? We’ll use our workhorse: the universal construction.

The second interesting question is, can any monoid be obtained from some free monoid by identifying more than the minimum number of elements required by the laws? I’ll show you that this follows directly from the universal construction.

Free Monoid Universal Construction

If you recall our previous experiences with universal constructions, you might notice that it’s not so much about constructing something as about selecting an object that best fits a given pattern. So if we want to use the universal construction to “construct” a free monoid, we have to consider a whole bunch of monoids from which to pick one. We need a whole category of monoids to chose from. But do monoids form a category?

Let’s first look at monoids as sets equipped with additional structure defined by unit and multiplication. We’ll pick as morphisms those functions that preserve the monoidal structure. Such structure-preserving functions are called homomorphisms. A monoid homomorphism must map the product of two elements to the product of the mapping of the two elements:

h (a * b) = h a * h b

and it must map unit to unit.
For instance, consider a homomorphism from lists of integers to integers. If we map [2] to 2 and [3] to 3, we have to map [2, 3] to 6, because concatenation

[2] ++ [3] = [2, 3]

becomes multiplication

2 * 3 = 6

Now let’s forget about the internal structure of individual monoids, and only look at them as objects with corresponding morphisms. You get a category Mon of monoids.

Okay, maybe before we forget about internal structure, let us notice an important property. Every object of Mon can be trivially mapped to a set. It’s just the set of its elements. This set is called the underlying set. In fact, not only can we map objects of Mon to sets, but we can also map morphisms of Mon (homomorphisms) to functions. Again, this seems sort of trivial, but it will become useful soon. This mapping of objects and morphisms from Mon to Set is in fact a functor. Since this functor “forgets” the monoidal structure — once we are inside a plain set, we no longer distinguish the unit element or care about multiplication — it’s called a forgetful functor. Forgetful functors come up regularly in category theory.

We now have two different views of Mon. We can treat it just like any other category with objects and morphisms. In that view, we don’t see the internal structure of monoids. All we can say about a particular object in Mon is that it connects to itself and to other objects through morphisms. The “multiplication” table of morphisms — the composition rules — are derived from the other view: monoids-as-sets. By going to category theory we haven’t lost this view completely — we can still access it through our forgetful functor.

To apply the universal construction, we need to define a special property that would let us search through the category of monoids and pick the best candidate for a free monoid. But a free monoid is defined by its generators. Different choices of generators produce different free monoids (a list of Bool is not the same as a list of Int). Our construction must start with a set of generators. So we’re back to sets!

That’s where the forgetful functor comes into play. We can use it to X-ray our monoids. We can identify the generators in the X-ray images of those blobs. Here’s how it works:

We start with a set of generators, x. That’s a set in Set.

The pattern we are going to match consists of a monoid m — an object of Mon — and a function p in Set:

p :: x -> U m

where U is our forgetful functor from Mon to Set. This is a weird heterogeneous pattern — half in Mon and half in Set.

The idea is that the function p will identify the set of generators inside the X-ray image of m. It doesn’t matter that functions may be lousy at identifying points inside sets (they may collapse them). It will all be sorted out by the universal construction, which will pick the best representative of this pattern.

We also have to define the ranking among candidates. Suppose we have another candidate: a monoid n and a function that identifies the generators in its X-ray image:

q :: x -> U n

We’ll say that m is better than n if there is a morphism of monoids (that’s a structure-preserving homomorphism):

h :: m -> n

whose image under U (remember, U is a functor, so it maps morphisms to functions) factorizes through p:

q = U h . p

If you think of p as selecting the generators in m; and q as selecting “the same” generators in n; then you can think of h as mapping these generators between the two monoids. Remember that h, by definition, preserves the monoidal structure. It means that a product of two generators in one monoid will be mapped to a product of the corresponding two generators in the second monoid, and so on.

This ranking may be used to find the best candidate — the free monoid. Here’s the definition:

We’ll say that m (together with the function p) is the free monoid with the generators x if and only if there is a unique morphism h from m to any other monoid n (together with the function q) that satisfies the above factorization property.

Incidentally, this answers our second question. The function U h is the one that has the power to collapse multiple elements of U m to a single element of U n. This collapse corresponds to identifying some elements of the free monoid. Therefore any monoid with generators x can be obtained from the free monoid based on x by identifying some of the elements. The free monoid is the one where only the bare minimum of identifications have been made.

We’ll come back to free monoids when we talk about adjunctions.

Challenges

You might think (as I did, originally) that the requirement that a homomorphism of monoids preserve the unit is redundant. After all, we know that for all a
```
h a * h e = h (a * e) = h a
```
So h e acts like a right unit (and, by analogy, as a left unit). The problem is that h a, for all a might only cover a sub-monoid of the target monoid. There may be a “true” unit outside of the image of h. Show that an isomorphism between monoids that preserves multiplication must automatically preserve unit.
Consider a monoid homomorphism from lists of integers with concatenation to integers with multiplication. What is the image of the empty list []? Assume that all singleton lists are mapped to the integers they contain, that is [3] is mapped to 3, etc. What’s the image of [1, 2, 3, 4]? How many different lists map to the integer 12? Is there any other homomorphism between the two monoids?
What is the free monoid generated by a one-element set? Can you see what it’s isomorphic to?

Next: Representable Functors.

Acknowledgments

I’d like to thank Gershom Bazerman for checking my math and logic, and André van Meulebrouck, who has been volunteering his editing help throughout this series of posts.
Follow @BartoszMilewski

July 13, 2015

From Lenses to Yoneda Embedding

Posted by Bartosz Milewski under Category Theory, Functional Programming, Haskell, Lens, Programming
[7] Comments

Lenses are a fascinating subject. Edward Kmett’s lens library is an indispensable tool in every Haskell programmer’s toolbox. I set out to write this blog post with the goal of describing some new insights into their categorical interpretation, but then I started reviewing all the different formulations of lenses and their relations to each other. So this post turned into a little summary of the theoretical underpinning of lenses.

If you’re already familiar with lenses, you may skip directly to the last section, which describes some new results.

The Data-Centric Picture

Lenses start as a very simple idea: an accessor/mutator or getter/setter pair — something familiar to every C++, Java, or C# programmer. In Haskell they can be described as two functions:

get :: s -> a
set :: s -> a -> s

Given an object of type s, the first function produces the value of the object’s sub-component of type a — which is the focus of the particular lens. The second function takes the object together with a new value for the sub-component, and produces a modified object.

A simple example is a lens that focuses on the first component of a pair:

get :: (a, a') -> a
get (x, y) = x

set :: (a, a') -> a -> (a, a')
set (x, y) x' = (x', y)

In Haskell we can go even further and define a lens for a polymorphic object, in which the setter changes not only the value of the sub-component, but also its type. This will, of course, also change the type of the resulting object. So, in general we have:

get :: s -> a
set :: s -> b -> t

Our pair example doesn’t change much on the surface:

get :: (a, a') -> a
get (x, y) = x

set :: (a, a') -> b -> (b, a')
set (x, y) x' = (x', y)

The difference is that the type of x' can now be different from the type of x. The first component of the pair is of type a before the update, and of type b (the same as that of x') after it. This way we can turn a pair of, say, (Int, Bool) to a pair of (String, Bool).

We can always go back to the monomorphic version of the lens by choosing b equal to a and t equal to s.

Not every pair of functions like these constitutes a lens. A lens has to obey a few laws (first formulated by Pierce in the database context). In particular, if you get a component after you set it, you should get back the value you just put in:

get . set s = id

If you call set with the value you obtained from get, you should get back the unchanged object:

set s (get s) = s

Finally, a set should overwrite the result of a previous set:

set (set s a) b = set s b

So this is what I would call a “classical” lens. It’s formulated in easy to understand programming terms.

The Algebraic Picture

It was Russell O’Connor who noticed that when you refactor the common element from the getter/setter pair, you get an interesting algebraic structure. Instead of writing the lens as two functions, we can write it as one function returning a pair:

s -> (a, b -> t)

Think of this as factoring out the “this” pointer in OO and returning the interface. Of course, the difference is that, in functional programming, the setter does not mutate the original — it returns a new version of the object instead.

Let’s for a moment concentrate on the monomorphic version of the lens — one in which a is the same as b, and s is the same as t. We can define a data structure:

data Store a s = Store a (a -> s)

and rewrite the lens as:

s -> Store a s

For instance, our first-component-of-a-pair lens will take the form:

fstl :: (a, b) -> Store a (a, b)
fstl (x, y) = Store x (\x' -> (x', y))

The first observation is that, for any a, Store a is a functor:

instance Functor (Store a) where
    fmap f (Store x h) = Store x (f . h)

It’s a well-known fact that you can define algebras for a functor, so-called F-algebras. An algebra for a functor f consists of a type s called the carrier type and a function called the action:

alg :: f s -> s

This is almost like a lens (with f replaced by Store a), except that the arrow goes the wrong way. Not to worry: there is a dual notion called a coalgebra. It consists of a carrier type s and a function:

coalg :: s -> f s

Substitute Store a for f and you see that a lens is nothing but a coalgebra for this functor. This is not saying much — we have just given a mathematical name to a programming construct, no big deal. Except that Store a is more than a functor — it’s also a comonad.

What’s a comonad? It’s a monad with the arrows reversed.

You know that you can define a monad in Haskell using return and join. Reverse the arrows on those two, and you get extract and duplicate, the two functions that define a comonad.

class (Functor w) => Comonad w where
    extract :: w a -> a
    duplicate :: w a -> w (w a)

Here, w is a type constructor that is also a functor.

This is how you can implement those two functions for Store a:

instance Comonad (Store a) where
    -- extract :: Store a s -> s
    extract (Store x h) = h x
    -- duplicate :: Store a s -> Store a (Store a s)
    duplicate (Store x h) = Store x (\y -> Store y h)

So now we have two structures: a comonad w and a coalgebra:

type Coalgebra w s = s -> w s

A lens is a special case of this coalgebra where w is Store a.

Every time you have two structures, you may legitimately ask the question: Are they compatible? Just by looking at types, you may figure out some obvious compatibility conditions. In particular, since they go the opposite way, it would make sense for extract to undo the action of coalg:

coalg :: Coalgebra w s
extract . coalg = id

Also, duplicating the result of coalg should be the same as applying coalg twice (the second time lifted by fmap):

fmap coalg . coalg = duplicate . coalg

If these two conditions are satisfied, we call coalg a comonad coalgebra.

And here’s the clencher:

These two conditions when applied to the Store a comonad are equivalent to our earlier lens laws.

Let’s see how it works. First we’ll express the result of our lens coalgebra acting on some object s in terms of get and set (curried set s is a function a->s):

coalg s = Store (get s) (set s)

The first condition extract . coalg = id immediately gives us the law:

set s (get s) = s

When we act with duplicate on coalg s, we get:

Store (get s) (\y -> Store y (set s))

On the other hand, when we fmap our coalg over coalg s, we get:

Store (get s) ((\s' -> Store (get s') (set s')) . set s)

Two functions — the second components of the Store objects in those equations — must be equal when acting on any a. The first function produces:

Store a (set s)

In the second one, we first apply set s to a to get set s a, which we then pass to the lambda to get:

Store (get (set s a)) (set (set s a))

This reproduces the other two (monomorphic) lens laws:

get (set s a) = a

and

set (set s a) = set s

This algebraic construction can be extended to type-changing lenses by replacing Store with its indexed version:

data IStore a b t = IStore a (b -> t)

and the comonad with its indexed counterpart. The indexed store is also called Context in the lens parlance, and an indexed comonad is also called a parametrized comonad.

So what’s an indexed comonad? Let’s start with an indexed functor. It’s a type constructor that takes three types, a, b, and s, and is a functor in the third argument:

class IxFunctor f where
    imap :: (s -> t) -> f a b s -> f a b t

IStore is obviously an indexed functor:

instance IxFunctor IStore where
    -- imap :: (s -> t) -> IStore a b s -> IStore a b t
    imap f (IStore x h) = IStore x (f . h)

An indexed comonad has the indexed versions of extract and duplicate:

class IxComonad w where
    iextract :: w a a t -> t
    iduplicate :: w a b t -> w a j (w j b t)

Notice that iextract is “diagonal” in the index types, whereas the double application of w shares one index, j, between the two applications. This plays very well with the unit and multiplication interpretation of a monad — here it looks just like matrix multiplication (although we are dealing with a comonad rather than a monad).

It’s easy to see that the instantiation of the indexed comonad for IStore works the same way as the instantiation of the comonad for Store. The types just work out that way.

instance IxComonad IStore where
    -- iextract :: IStore a a t -> t
    iextract (IStore a h) = h a
    -- iduplicate :: IStore a b t -> IStore a c (IStore c b t)
    iduplicate (IStore a h) = IStore a (\c -> IStore c h)

There is also an indexed version of a comonad coalgebra, where the coalgebra is replaced by a family of mappings from some carrier type s to w a b t; with the type t determined by s together with the choice of of the indexes a and b:

type ICoalg w s t a b = s -> w a b t

The compatibility conditions that make it an (indexed) comonad coalgebra are almost identical to the standard compatibility conditions, except that we have to be careful about the index types. Here’s the first condition:

icoalg_aa :: ICoalg w s t a a
iextract . icoalg_aa = id

Let’s analyze the types. The inner part has the type:

icoalg_aa :: s -> w a a t

We apply iextract to it, which has the type:

iextract :: w a a t -> t

and get:

iextract . icoalg_aa :: s -> t

The right hand side of the condition has the type:

id :: s -> s

It follows that, for the diagonal components of ICoalg w s t, t must be equal to s. The diagonal part of ICoalg w s t is therefore a family of regular coalgebras.

As we have done with the monomorphic lens, we can express (ICoalg IStore s t a b), when acting on s, in terms of get and set:

icoalg_ab s = IStore (get s) (set s)

But now get s is of type a, while set s if of the type b -> t. We can still apply extract to the diagonal term IStore a a t as required by the first compatibility condition. When equating the result to id, we recover the lens law:

set s (get s) = s

Similarly, it’s straightforward to see that the second compatibility condition:

icoalg_bc :: ICoalg w s t b c
icoalg_ab :: ICoalg w s t a b
icoalg_ac :: ICoalg w s t a c
imap icoalg_bc . icoalg_ab = iduplicate . icoalg_ac

is equivalent to the other two lens laws.

The Parametric Picture

Despite being theoretically attractive, standard lenses were awkward to use and, in particular, to compose. The breakthrough came when Twan van Laarhoven realized that there is a higher-order representation for them that has very nice compositional properties. Composing lenses to focus on sub-objects of sub-objects turned into simple function composition.

Here’s Twan’s representation (generalized by Russell for the polymorphic case):

type Lens s t a b = forall f. Functor f => (a -> f b) -> (s -> f t)

So a lens is a polymorphic higher order function with a twist. The twist is that it’s polymorphic with respect to a functor rather than a type.

You can think of it this way: the caller provides a function to modify a particular field of s, turning it from type a to f b. What the caller gets back is a function that transforms the whole of s to f t. The idea is that the lens knows how to reconstruct the object, while putting it under a functor f — if you tell it how to modify a field, also under this functor.

For instance, continuing with our example, here’s the van Laarhoven lens that focuses on the first component of a pair:

vL :: Lens (a, c) (b, c) a b
vL h (x, x') = fmap (\y -> (y, x')) (h x)

Here, s is (a, c) and t is (b, c).

To see that the van Laarhoven representation is equivalent to the get/set one, let’s first change the order of arguments and pull s outside of the forall quantifier:

Lens s t a b = s -> (forall f. Functor f => (a -> f b) -> f t)

Here’s how you can read this definition: For a given s, if you give me a function from a to f b, I will produce a value of type f t. And I don’t care what functor you use!

What does it mean not to care about the functor? It means that the lens must be parametrically polymorphic in f. It can’t do case analysis on a functor. It must be implemented using the same formula for f being the list functor, or the Maybe functor, or the Const functor, etc. There’s only one thing all these functors have in common, and that’s the fmap function; so that’s what we are allowed to use in the implementation of the lens.

Now let’s think what we can do with a function a -> f b that we were given. There’s only one thing: apply it to some value of type a. So we must have access to a value of type a. The result of this application is some value of type f b, but we need to produce a value of the type f t. The only way to do it is to have a function of type b->t and sneak it under the functor using fmap (so here’s where the generic functor comes in). We conclude that the implementation of the function:

forall f. Functor f => (a -> f b) -> f t

must be hiding a value of type a and a function b->t. But that’s exactly the contents of IStore a b t. Parametricity tells us that there is an IStore hiding inside the van Laarhoven lens. The lens is equivalent to:

s -> IStore a b t

In fact, with a clever choice of functors we can recover both get and set from the van Laarhoven representation.

First we select our functor to be Const a. Note that the parameter a is not the one over which the functor is defined. Const a takes a second parameter b over which it is functorial. And, even though it takes b as a type parameter, it doesn’t use it at all. Instead, like a magician, it palms an a, and then reveals it at the end of the trick.

newtype Const a b = Const { getConst :: a }

instance Functor (Const a) where
    -- fmap :: (s -> t) -> Const a s -> Const a t
    fmap _ (Const a) = (Const a)

The constructor Const happens to be a function

Const :: a -> Const a b

which has the required form to be the first argument to the lens:

a -> f b

When we apply the lens, let’s call it vL, to the function Const, we get another function:

vL Const :: s -> Const a t

We can apply this function to s, and then, in the final reveal, retrieve the value of a that was smuggled inside Const a:

get vL s = getConst $ vL Const s

Similarly, we can recover set from the van Laarhoven lens using the Identity functor:

newtype Identity a = Identity { runIdentity :: a }

We define:

set vL s x = runIdentity $ vL (Identity . const x) s

The beauty of the van Laarhoven representation is that it composes lenses using simple function composition. A lens takes a function and returns a function. This function can, in turn, be passed as the argument to another lens, and so on.

There’s an interesting twist to this kind of composition — the function composition operator in Haskell is the dot, just like the field accessor in OO languages like Java or C++; and the composition follows the same order as the composition of accessors in those languages. This was first observed by Conal Elliott in the context of semantic editor combinators.

Consider a lens that focuses on the a field inside some object s. It’s type is:

Lens s t a b

When given a function:

h :: a -> f b

it returns a function:

h' :: s -> f t

Now consider another lens that focuses on the s field inside some even bigger object u. It’s type is:

Lens u w s t

It expects a function of the type:

g :: s -> f t

We can pass the result of the first lens directly to the second lens to form a composite:

Lens u w s t . Lens s t a b

We get a lens that focuses on the a field of the object s that is the sub-object of the big object u. It works just like in Java, where you apply a dot to the result of a getter or a setter, to dig deeper into a subobject.

Not only do lenses compose using regular function composition, but we can also use the identity function as the identity lens. So lenses form a category. It’s time to have a serious look at category theory. Warning: Heavy math ahead!

The Categorical Picture

I used parametricity arguments to justify the choice of the van Laarhoven representation for the lens. The lens function is supposed to have the same form for all functors f. Parametricity arguments have an operational feel to them, which is okay, but I feel like a solid categorical justification is more valuable than any symbol-shuffling argument. So I worked on it, and eventually came up with a derivation of the van Laarhoven representation using the Yoneda lemma. Apparently Russell O’Connor and Mauro Jaskelioff had similar feelings because they came up with the same result independently. We used the same approach, going through the Store functor and applying the Yoneda lemma twice, once in the functor category, and once in the Set category (see the Bibliography).

I would like to present the same result in a more general setting of the Yoneda embedding. It’s a direct consequence of the Yoneda lemma, and it states that any category can be embedded (fully and faithfully) in the category of functors from that category to Set.

Here’s how it works: Let’s fix some object a in some category C. For any object x in that category there is a hom-set C(a, x) of morphisms from a to x. A hom-set is a set — an object in the category Set of sets. So we have defined a mapping from C to Set that takes an x and maps it to the set C(a, x). This mapping is called C(a, _), with the underscore serving as a placeholder for the argument.

It’s easy to convince yourself that this mapping is in fact a functor from C to Set. Indeed, take any morphism f from x to y. We want to map this morphism to a function (a morphism in Set) that goes between C(a, x) and C(a, y). Let’s define this lifted function component-wise: given any element h from C(a, x) we can map it to f . h. It’s just a composition of two morphisms from C. The resulting morphism is a member of C(a, y). We have lifted a morphism f from C to Set thus establishing that C(a, _) is a functor.

Now consider two such functors, C(a, _) and C(b, _). The Yoneda embedding theorem tells us that there is a one-to-one correspondence between the set of natural transformations between these two functors and the hom-set C(b, a).

Nat(C(a, _), C(b, _)) ≅ C(b, a)

Notice the reversed order of a and b on the right-hand side.

Let’s rephrase what we have just seen. For every a in C, we can define a functor C(a, _) from C to Set. Such a functor is a member of the functor category Fun(C, Set). So we have a mapping from C to the functor category Fun(C, Set). Is this mapping a functor?

We have just seen that there is a mapping between morphisms in C and natural transformations in Fun(C, Set) — that’s the gist of the Yoneda embedding. But natural transformations are morphisms in the functor category. So we do have a functor from C to the functor category Fun(C, Set). It maps objects to objects and morphisms to morphisms. It’s a contravariant functor, because of the reversal of a and b. Moreover, it maps the hom-sets in the two categories one-to-one, so it’s a fully faithful functor, and therefore it defines an embedding of categories. Every category C can be embedded in the functor category Fun(C, Set). That’s called the Yoneda embedding.

There’s an interesting consequence of the Yoneda embedding: Every functor category can be embedded in its own functor category — just replace C with a functor category in the Yoneda embedding. Recall that functors between any two categories form a category. It’s a category in which objects are functors and morphisms are natural transformations. Yoneda embedding works for that category too, which means that a functor category can be embedded in a category of functors from that functor category to Set.

Let’s see what that means. We can fix one functor, say R and consider the hom-set from R to some arbitrary functor f. Since we are in a functor category, this hom-set is a set of natural transformations between the two functors, Nat(R, f).

Now let’s pick another functor S. It also defines a set of natural transformations Nat(S, f). We can keep picking functors and mapping them to sets (sets of natural transformations). In fact we know from the previous argument that this mapping is itself a functor. This time it’s a functor from a functor category to Set.

What does the Yoneda embedding tell us about any two such functors? That the set of natural transformations between them is isomorphic to the (reversed) hom-set. But this time hom-sets are sets of natural transformations. So we have:

Nat(Nat(R, _), Nat(S, _)) ≅ Nat(S, R)

All natural transformations in this formula are regular natural transformation except for the outer one, which is more interesting. You may recall that a natural transformation is a family of morphisms parameterized by objects. But in this case objects are functors, and morphisms are themselves natural transformations. So it’s a family of natural transformations parameterized by functors. Keep this in mind as we proceed.

To get a better feel of what’s happening, let’s translate this to Haskell. In Haskell we represent natural transformations as polymorphic functions. This makes sense, since a natural transformation is a family of morphisms (here functions) parameterized by objects (here types). So a member of Nat(R, f) can be represented as:

forall x. R x -> f x

Similarly, the second natural transformation in our formula turns into:

forall y. S y -> f y

As I said, the outer natural transformation in the Yoneda embedding is a family of natural transformations parameterized by a functor, so we get:

forall f. Functor f => (forall x. R x -> f x) -> (forall y. S y -> f y)

You can already see one element of the van Laarhoven representation: the quantification over a functor.

The right hand side of the Yoneda embedding is a natural transformation:

forall z. S z -> R z

The next step is to pick the appropriate functors for R and S. We’ll take R to be IStore a b and S to be IStore s t.

Let’s work on the first part:

forall x. IStore a b x -> f x

A function from IStore a b x is equivalent to a function of two arguments, one of them of type a and another of type b->x:

forall x. a -> (b -> x) -> f x

We can pull a out of forall to get:

a -> (forall x. (b -> x) -> f x)

If you squint a little, you recognize that the thing in parentheses is a natural transformation between the functor C(b, _) and f, where C is the category of Haskell types. We can now apply the Yoneda lemma, which says that this set of natural transformations is isomorphic to the set f b:

forall x. (b -> x) -> f x ≅ f b

We can apply the same transformation to the second part of our identity:

forall y. (IStore s t y -> f y) ≅ s -> f t

Taking it all together, we get:

forall f. Functor f => (a -> f b) -> (s -> f t) 
    ≅ forall z. IStore s t z -> IStore a b z

Let’s now work on the right hand side:

forall z. IStore s t z -> IStore a b z 
    ≅ forall z. s -> (t -> z) -> IStore a b z

Again, pulling s out of forall and applying the Yoneda lemma, we get:

s -> IStore a b t

But that’s just the standard representation of the lens:

s -> IStore a b t ≅ (s -> a, s -> b -> t) = (get, set)

Thus the Yoneda embedding of the functor category leads to the van Laarhoven representation of the lens:

forall f. Functor f => (a -> f b) -> (s -> ft) 
  ≅ (s -> a, s -> b -> t)

Playing with Adjunctions

This is all very satisfying, but you may wonder what’s so special about the IStore functor? The crucial step in the derivation of the van Laarhoven representation was the application of the Yoneda lemma to get this identity:

forall x. IStore a b x -> f x ≅ a -> f b

Let’s rewrite it in the more categorical language:

Nat(IStore a b, f) ≅ C(a, f b)

The set of natural transformations from the functor IStore a b to the functor f is isomorphic to the hom-set between a and f b. Any time you see an isomorphism of hom-sets (and remember that Nat is the hom-set in the functor category), you should be on the lookout for an adjunction. And indeed, we have an adjunction between two functors. One functor is defined as:

a -> IStore a b

It takes an object a in C and maps it to a functor IStore a b parameterized by some other object b. The other functor is:

f -> f b

It maps a functor, an object in the functor category, to an object in C. This functor is also parameterized by the same b. Since this is a flipped application, I’ll call it Flapp:

newtype Flapp b f = Flapp (f b)

So, for any b, the functor-valued functor IStore _ b is left adjoint to Flapp b. This is what makes IStore special.

As a side note: IStore a b is a covariant functor in a and a contravariant functor in b. However, Store a is not functorial in a, because a appears in both positive and negative position in its definition. So the adjunction trick doesn’t work for a simple (monomorphic) lens.

We can now turn the tables and use the adjunction to define the functor IStore in an arbitrary category (notice that the Yoneda lemma worked only for Set-valued functors). We just define a functor-valued functor IStore to be the left adjoint to Flapp, provided it exists.

Nat(IStore a b, f) ≅ C(a, f b)

Here, Nat is a set of natural transformations between endofunctors in C.

We can substitute the so defined functor into the Yoneda embedding formula we used earlier:

Nat((Nat(IStore a b, f), Nat(IStore s t, f)) 
    ≅ Nat(IStore s t, IStore a b)

We can now use the adjunction, rather than the Yoneda lemma, to eliminate some of the occurrences IStore:

Nat(C(a, f b), C(s, f t))
    ≅ C(s, IStore a b t)

This is slightly more general than the original van Laarhoven equivalence.

We can go even farther and reproduce the Jaskelioff and O’Connor trick of constraining the generic functor in the definition of the van Laarhoven lens to a pointed or applicative functor. This results in a multi-focus lens. In particular, if we use pointed functors, we get lenses with zero or one targets, so called affine lenses. Restricting the functors further to applicative leads to lenses with any number of targets, or traversals.

The trick is that any pointed or applicative functor can be stripped of the additional functionality and treated just like any other functor. This act of “forgetting” about pure and <*> may itself be considered a functor in the functor category. It’s called, appropriately, a forgetful functor. The left adjoint to a forgetful functor (if it exists) is called a free functor. It takes an arbitrary functor and creates a pointed functor by generating an artificial pure; or it creates an applicative functor by adding <*>. This adjunction is described by a natural isomorphism of hom-sets — in this case sets of natural transformations:

Nat(S, U f) ≅ Nat(S*, f)

Here, U is the forgetful functor, and S* is the free applicative/pointed version of the functor S. The functor f ranges across applicative (respectively, pointed) functors.

Now we can try to substitute the free version of IStore in the Yoneda embedding formula:

Nat((Nat(IStore* a b, f), Nat(IStore* s t, f)) 
    ≅ Nat(IStore* s t, IStore* a b)

The formula holds for any applicative (pointed) functor f and a set of natural transformations over such functors.

The first step is to use the forgetful/free adjunction:

Nat((Nat(IStore a b, U f), Nat(IStore s t, U f)) 
    ≅ Nat(IStore s t, U IStore* a b)

Then we can use our defining adjunction for IStore to get:

Nat(C(a, U f b), C(s, U f t)) 
    ≅ C(s, U IStore* a b t)

In Haskell notation this reads:

forall f. Applicative f => (a -> f b) -> (s -> f t)
    ≅ s -> IAppStore a b t

(the action of U is implicit).

The free applicative version of IStore is defined as:

data IAppStore a b t = 
    Unit t
  | IAppStore a (IAppStore a b (b -> t))

These are all known results, but the use of the Yoneda embedding and the adjunction to define the IStore functor makes the derivation more compact and slightly more general.

Acknowledgments

I’m grateful to Mauro Jaskelioff, Gershom Bazerman, and Joseph Abrahamson for reading the draft and providing helpful comments and to André van Meulebrouck for editing help.

Bibliography

Edward Kmett, The Haskell Lens Library
Simon Peyton Jones, Lenses: Compositional Data Access and Manipulation. A Skills Matter video presentation.
Joseph Abrahamson, A Little Lens Starter Tutorial
Joseph Abrahamson, Lenses from Scratch
Artyom, lens over tea tutorial
Twan van Laarhoven, CPS based functional references
Bartosz Milewski, Lenses, Stores, and Yoneda
Mauro Jaskelioff, Russell O’Connor, A Representation Theorem for Second-Order Functionals
Bartosz Milewski, Understanding Yoneda

May 11, 2015

Using Monads in C++ to Solve Constraints: 1. The List Monad

Posted by Bartosz Milewski under C++, Functional Programming, Haskell, Monads, Programming
[26] Comments

I am sometimes asked by C++ programmers to give an example of a problem that can’t be solved without monads. This is the wrong kind of question — it’s like asking if there is a problem that can’t be solved without for loops. Obviously, if your language supports a goto, you can live without for loops. What monads (and for loops) can do for you is to help you structure your code. The use of loops and if statements lets you convert spaghetti code into structured code. Similarly, the use of monads lets you convert imperative code into declarative code. These are the kind of transformations that make code easier to write, understand, maintain, and generalize.

So here’s a problem that you may get as an interview question. It’s a small problem, so the advantages of various approaches might not be immediately obvious, especially if you’ve been trained all your life in imperative programming, and you are seeing monads for the first time.

You’re supposed write a program to solve this puzzle:

  s e n d
+ m o r e
---------
m o n e y

Each letter correspond to a different digit between 0 and 9. Before you continue reading this post, try to think about how you would approach this problem.

The Analysis

It never hurts to impress your interviewer with your general knowledge by correctly classifying the problem. This one belongs to the class of “constraint satisfaction problems.” The obvious constraint is that the numbers obtained by substituting letters with digits have to add up correctly. There are also some less obvious constraints, namely the numbers should not start with zero.

If you were to solve this problem using pencil and paper, you would probably come up with lots of heuristics. For instance, you would deduce that m must stand for 1 because that’s the largest possible carry from the addition of two digits (even if there is a carry from the previous column). Then you’d figure out that s must be either 8 or 9 to produce this carry, and so on. Given enough time, you could probably write an expert system with a large set of rules that could solve this and similar problems. (Mentioning an expert system could earn you extra points with the interviewer.)

However, the small size of the problem suggests that a simple brute force approach is probably best. The interviewer might ask you to estimate the number of possible substitutions, which is 10!/(10 – 8)! or roughly 2 million. That’s not a lot. So, really, the solution boils down to generating all those substitutions and testing the constraints for each.

The Straightforward Solution

The mind of an imperative programmer immediately sees the solution as a set of 8 nested loops (there are 8 unique letters in the problem: s, e, n, d, m, o, r, y). Something like this:

for (int s = 0; s < 10; ++s)
    for (int e = 0; e < 10; ++e)
        for (int n = 0; n < 10; ++n)
            for (int d = 0; d < 10; ++d)
                ...

and so on, until y. But then there is the condition that the digits have to be different, so you have to insert a bunch of tests like:

e != s
n != s && n != e
d != s && d != e && d != n

and so on, the last one involving 7 inequalities… Effectively you have replaced the uniqueness condition with 28 new constraints.

This would probably get you through the interview at Microsoft, Google, or Facebook, but really, can’t you do better than that?

The Smart Solution

Before I proceed, I should mention that what follows is almost a direct translation of a Haskell program from the blog post by Justin Le. I strongly encourage everybody to learn some Haskell, but in the meanwhile I’ll be happy to serve as your translator.

The problem with our naive solution is the 28 additional constraints. Well, I guess one could live with that — except that this is just a tiny example of a whole range of constraint satisfaction problems, and it makes sense to figure out a more general approach.

The problem can actually be formulated as a superposition of two separate concerns. One deals with the depth and the other with the breadth of the search for solutions.

Let me touch on the depth issue first. Let’s consider the problem of creating just one substitution of letters with numbers. This could be described as picking 8 digits from a list of 0, 1, …9, one at a time. Once a digit is picked, it’s no longer in the list. We don’t want to hard code the list, so we’ll make it a parameter to our algorithm. Notice that this approach works even if the list contains duplicates, or if the list elements are not easily comparable for equality (for instance, if they are futures). We’ll discuss the list-picking part of the problem in more detail later.

Now let’s talk about breadth: we have to repeat the above process for all possible picks. This is what the 8 nested loops were doing. Except that now we are in trouble because each individual pick is destructive. It removes items from the list — it mutates the list. This is a well known problem when searching through solution spaces, and the standard remedy is called backtracking. Once you have processed a particular candidate, you put the elements back in the list, and try the next one. Which means that you have to keep track of your state, either implicitly on your function’s stack, or in a separate explicit data structure.

Wait a moment! Weren’t we supposed to talk about functional programming? So what’s all this talk about mutation and state? Well, who said you can’t have state in functional programming? Functional programmers have been using the state monad since time immemorial. And mutation is not an issue if you’re using persistent data structures. So fasten your seat belts and make sure your folding trays are in the upright position.

The List Monad

We’ll start with a small refresher in quantum mechanics. As you may remember from school, quantum processes are non-deterministic. You may repeat the same experiment many times and every time get a different result. There is a very interesting view of quantum mechanics called the many-worlds interpretation, in which every experiment gives rise to multiple alternate histories. So if the spin of an electron may be measured as either up or down, there will be one universe in which it’s up, and one in which it’s down.

We’ll use the same approach to solving our puzzle. We’ll create an alternate universe for each digit substitution for a given letter. So we’ll start with 10 universes for the letter s; then we’ll split each of them into ten universes for the letter e, and so on. Of course, most of these universes won’t yield the desired result, so we’ll have to destroy them. I know, it seems kind of wasteful, but in functional programming it’s easy come, easy go. The creation of a new universe is relatively cheap. That’s because new universes are not that different from their parent universes, and they can share almost all of their data. That’s the idea behind persistent data structures. These are the immutable data structures that are “mutated” by cloning. A cloned data structure shares most of its implementation with the parent, except for a small delta. We’ll be using persistent lists described in my earlier post.

Once you internalize the many-worlds approach to programming, the implementation is pretty straightforward. First, we need functions that generate new worlds. Since we are cheap, we’ll only generate the parts that are different. So what’s the difference between all the worlds that we get when selecting the substitution for the letter s? Just the number that we assign to s. There are ten worlds corresponding to the ten possible digits (we’ll deal with the constraints like s being different from zero later). So all we need is a function that generates a list of ten digits. These are our ten universes in a nutshell. They share everything else.

Once you are in an alternate universe, you have to continue with your life. In functional programming, the rest of your life is just a function called a continuation. I know it sounds like a horrible simplification. All your actions, emotions, and hopes reduced to just one function. Well, maybe the continuation just describes one aspect of your life, the computational part, and you can still hold on to our emotions.

So what do our lives look like, and what do they produce? The input is the universe we’re in, in particular the one number that was picked for us. But since we live in a quantum universe, the outcome is a multitude of universes. So a continuation takes a number, and produces a list. It doesn’t have to be a list of numbers, just a list of whatever characterizes the differences between alternate universes. In particular, it could be a list of different solutions to our puzzle — triples of numbers corresponding to “send”, “more”, and “money”. (There is actually only one solution, but that’s beside the point.)

And what’s the very essence of this new approach? It’s the binding of the selection of the universes to the continuation. That’s where the action is. This binding, again, can be expressed as a function. It’s a function that takes a list of universes and a continuation that produces a list of universes. It returns an even bigger list of universes. We’ll call this function for_each, and we’ll make it as generic as possible. We won’t assume anything about the type of the universes that are passed in, or the type of the universes that the continuation k produces. We’ll also make the type of the continuation a template parameter and extract the return type from it using auto and decltype:

template<class A, class F>
auto for_each(List<A> lst, F k) -> decltype(k(lst.front()))
{
    using B = decltype(k(lst.front()).front());
    // This should really be expressed using concepts
    static_assert(std::is_convertible<
        F, std::function<List<B>(A)>>::value,
        "for_each requires a function type List<B>(A)");

    List<List<B>> lstLst = fmap(k, lst);
    return concatAll(lstLst);
}

The function fmap is similar to std::transform. It applies the continuation k to every element of the list lst. Because k itself produces a list, the result is a list of lists, lstLst. The function concatAll concatenates all those lists into one big list.

Congratulations! You have just seen a monad. This one is called the list monad and it’s used to model non-deterministic processes. The monad is actually defined by two functions. One of them is for_each, and here’s the other one:

template<class A>
List<A> yield(A a)
{
    return List<A> (a);
}

It’s a function that returns a singleton list. We use yield when we are done multiplying universes and we just want to return a single value. We use it to create a single-valued continuation. It represents the lonesome boring life, devoid of any choices.

I will later rename these functions to mbind and mreturn, because they are part of any monad, not just the list monad.

The names like for_each or yield have a very imperative ring to them. That’s because, in functional programming, monadic code plays a role similar to imperative code. But neither for_each nor yield are control structures — they are functions. In particular for_each, which sounds and works like a loop, is just a higher order function; and so is fmap, which is used in its implementation. Of course, at some level the code becomes imperative — fmap can either be implemented recursively or using an actual loop — but the top levels are just declarations of functions. Hence, declarative programming.

There is a slight difference between a loop and a function on lists like for_each: for_each takes a whole list as an argument, while a loop might generate individual items — in this case integers — on the fly. This is not a problem in a lazy functional language like Haskell, where a list is evaluated on demand. The same behavior may be implemented in C++ using streams or lazy ranges. I won’t use it here, since the lists we are dealing with are short, but you can read more about it in my earlier post Getting Lazy with C++.

We are not ready yet to implement the solution to our puzzle, but I’d like to give you a glimpse of what it looks like. For now, think of StateL as just a list. See if it starts making sense (I grayed out the usual C++ noise):

StateL<tuple<int, int, int>> solve()
{
    StateL<int> sel = &select<int>;

    return for_each(sel, [=](int s) {
    return for_each(sel, [=](int e) {
    return for_each(sel, [=](int n) {
    return for_each(sel, [=](int d) {
    return for_each(sel, [=](int m) {
    return for_each(sel, [=](int o) {
    return for_each(sel, [=](int r) {
    return for_each(sel, [=](int y) {
        return yield_if(s != 0 && m != 0, [=]() {
            int send  = asNumber(vector{s, e, n, d});
            int more  = asNumber(vector{m, o, r, e});
            int money = asNumber(vector{m, o, n, e, y});
            return yield_if(send + more == money, [=]() {
                return yield(make_tuple(send, more, money));
            });
        });
    });});});});});});});});
}

The first for_each takes a selection of integers, sel, (never mind how we deal with uniqueness); and a continuation, a lambda, that takes one integer, s, and produces a list of solutions — tuples of three integers. This continuation, in turn, calls for_each with a selection for the next letter, e, and another continuation that returns a list of solutions, and so on.

The innermost continuation is a conditional version of yield called yield_if. It checks a condition and produces a zero- or one-element list of solutions. Internally, it calls another yield_if, which calls the ultimate yield. If that final yield is called (and it might not be, if one of the previous conditions fails), it will produce a solution — a triple of numbers. If there is more than one solution, these singleton lists will get concatenated inside for_each while percolating to the top.

In the second part of this post I will come back to the problem of picking unique numbers and introduce the state monad. You can also have a peek at the code on github.

Challenges

Implement for_each and yield for a vector instead of a List. Use the Standard Library transform instead of fmap.
Using the list monad (or your vector monad), write a function that generates all positions on a chessboard as pairs of characters between 'a' and 'h' and numbers between 1 and 8.
Implement a version of for_each (call it repeat) that takes a continuation k of the type function<List<B>()> (notice the void argument). The function repeat calls k for each element of the list lst, but it ignores the element itself.

April 7, 2015

Natural Transformations

Posted by Bartosz Milewski under Category Theory, Functional Programming, Haskell, Programming
[68] Comments

This is part 10 of Categories for Programmers. Previously: Function Types. See the Table of Contents.

We talked about functors as mappings between categories that preserve their structure. A functor “embeds” one category in another. It may collapse multiple things into one, but it never breaks connections. One way of thinking about it is that with a functor we are modeling one category inside another. The source category serves as a model, a blueprint, for some structure that’s part of the target category.

There may be many ways of embedding one category in another. Sometimes they are equivalent, sometimes very different. One may collapse the whole source category into one object, another may map every object to a different object and every morphism to a different morphism. The same blueprint may be realized in many different ways. Natural transformations help us compare these realizations. They are mappings of functors — special mappings that preserve their functorial nature.

Consider two functors F and G between categories C and D. If you focus on just one object a in C, it is mapped to two objects: F a and G a. A mapping of functors should therefore map F a to G a.

Notice that F a and G a are objects in the same category D. Mappings between objects in the same category should not go against the grain of the category. We don’t want to make artificial connections between objects. So it’s natural to use existing connections, namely morphisms. A natural transformation is a selection of morphisms: for every object a, it picks one morphism from F a to G a. If we call the natural transformation α, this morphism is called the component of α at a, or α_a.

α_a :: F a -> G a

Keep in mind that a is an object in C while α_a is a morphism in D.

If, for some a, there is no morphism between F a and G a in D, there can be no natural transformation between F and G.

Of course that’s only half of the story, because functors not only map objects, they map morphisms as well. So what does a natural transformation do with those mappings? It turns out that the mapping of morphisms is fixed — under any natural transformation between F and G, F f must be transformed into G f. What’s more, the mapping of morphisms by the two functors drastically restricts the choices we have in defining a natural transformation that’s compatible with it. Consider a morphism f between two objects a and b in C. It’s mapped to two morphisms, F f and G f in D:

F f :: F a -> F b
G f :: G a -> G b

The natural transformation α provides two additional morphisms that complete the diagram in D:

α_a :: F a -> G a
α_b :: F b -> G b

Now we have two ways of getting from F a to G b. To make sure that they are equal, we must impose the naturality condition that holds for any f:

G f ∘ α_a = α_b ∘ F f

The naturality condition is a pretty stringent requirement. For instance, if the morphism F f is invertible, naturality determines α_b in terms of α_a. It transports α_a along f:

α_b = (G f) ∘ α_a ∘ (F f)^-1

If there is more than one invertible morphism between two objects, all these transports have to agree. In general, though, morphisms are not invertible; but you can see that the existence of natural transformations between two functors is far from guaranteed. So the scarcity or the abundance of functors that are related by natural transformations may tell you a lot about the structure of categories between which they operate. We’ll see some examples of that when we talk about limits and the Yoneda lemma.

Looking at a natural transformation component-wise, one may say that it maps objects to morphisms. Because of the naturality condition, one may also say that it maps morphisms to commuting squares — there is one commuting naturality square in D for every morphism in C.

This property of natural transformations comes in very handy in a lot of categorical constructions, which often include commuting diagrams. With a judicious choice of functors, a lot of these commutativity conditions may be transformed into naturality conditions. We’ll see examples of that when we get to limits, colimits, and adjunctions.

Finally, natural transformations may be used to define isomorphisms of functors. Saying that two functors are naturally isomorphic is almost like saying they are the same. Natural isomorphism is defined as a natural transformation whose components are all isomorphisms (invertible morphisms).

Polymorphic Functions

We talked about the role of functors (or, more specifically, endofunctors) in programming. They correspond to type constructors that map types to types. They also map functions to functions, and this mapping is implemented by a higher order function fmap (or transform, then, and the like in C++).

To construct a natural transformation we start with an object, here a type, a. One functor, F, maps it to the type F a. Another functor, G, maps it to G a. The component of a natural transformation alpha at a is a function from F a to G a. In pseudo-Haskell:

alpha_a :: F a -> G a

A natural transformation is a polymorphic function that is defined for all types a:

alpha :: forall a . F a -> G a

The forall a is optional in Haskell (and in fact requires turning on the language extension ExplicitForAll). Normally, you would write it like this:

alpha :: F a -> G a

Keep in mind that it’s really a family of functions parameterized by a. This is another example of the terseness of the Haskell syntax. A similar construct in C++ would be slightly more verbose:

template<class A> G<A> alpha(F<A>);

There is a more profound difference between Haskell’s polymorphic functions and C++ generic functions, and it’s reflected in the way these functions are implemented and type-checked. In Haskell, a polymorphic function must be defined uniformly for all types. One formula must work across all types. This is called parametric polymorphism.

C++, on the other hand, supports by default ad hoc polymorphism, which means that a template doesn’t have to be well-defined for all types. Whether a template will work for a given type is decided at instantiation time, where a concrete type is substituted for the type parameter. Type checking is deferred, which unfortunately often leads to incomprehensible error messages.

In C++, there is also a mechanism for function overloading and template specialization, which allows different definitions of the same function for different types. In Haskell this functionality is provided by type classes and type families.

Haskell’s parametric polymorphism has an unexpected consequence: any polymorphic function of the type:

alpha :: F a -> G a

where F and G are functors, automatically satisfies the naturality condition. Here it is in categorical notation (f is a function f::a->b):

G f ∘ α_a = α_b ∘ F f

In Haskell, the action of a functor G on a morphism f is implemented using fmap. I’ll first write it in pseudo-Haskell, with explicit type annotations:

fmap_G f . alpha_a = alpha_b . fmap_F f

Because of type inference, these annotations are not necessary, and the following equation holds:

fmap f . alpha = alpha . fmap f

This is still not real Haskell — function equality is not expressible in code — but it’s an identity that can be used by the programmer in equational reasoning; or by the compiler, to implement optimizations.

The reason why the naturality condition is automatic in Haskell has to do with “theorems for free.” Parametric polymorphism, which is used to define natural transformations in Haskell, imposes very strong limitations on the implementation — one formula for all types. These limitations translate into equational theorems about such functions. In the case of functions that transform functors, free theorems are the naturality conditions. [You may read more about free theorems in my blog Parametricity: Money for Nothing and Theorems for Free.]

One way of thinking about functors in Haskell that I mentioned earlier is to consider them generalized containers. We can continue this analogy and consider natural transformations to be recipes for repackaging the contents of one container into another container. We are not touching the items themselves: we don’t modify them, and we don’t create new ones. We are just copying (some of) them, sometimes multiple times, into a new container.

The naturality condition becomes the statement that it doesn’t matter whether we modify the items first, through the application of fmap, and repackage later; or repackage first, and then modify the items in the new container, with its own implementation of fmap. These two actions, repackaging and fmapping, are orthogonal. “One moves the eggs, the other boils them.”

Let’s see a few examples of natural transformations in Haskell. The first is between the list functor, and the Maybe functor. It returns the head of the list, but only if the list is non-empty:

safeHead :: [a] -> Maybe a
safeHead [] = Nothing
safeHead (x:xs) = Just x

It’s a function polymorphic in a. It works for any type a, with no limitations, so it is an example of parametric polymorphism. Therefore it is a natural transformation between the two functors. But just to convince ourselves, let’s verify the naturality condition.

fmap f . safeHead = safeHead . fmap f

We have two cases to consider; an empty list:

fmap f (safeHead []) = fmap f Nothing = Nothing

safeHead (fmap f []) = safeHead [] = Nothing

and a non-empty list:

fmap f (safeHead (x:xs)) = fmap f (Just x) = Just (f x)

safeHead (fmap f (x:xs)) = safeHead (f x : fmap f xs) = Just (f x)

I used the implementation of fmap for lists:

fmap f [] = []
fmap f (x:xs) = f x : fmap f xs

and for Maybe:

fmap f Nothing = Nothing
fmap f (Just x) = Just (f x)

An interesting case is when one of the functors is the trivial Const functor. A natural transformation from or to a Const functor looks just like a function that’s either polymorphic in its return type or in its argument type.

For instance, length can be thought of as a natural transformation from the list functor to the Const Int functor:

length :: [a] -> Const Int a
length [] = Const 0
length (x:xs) = Const (1 + unConst (length xs))

Here, unConst is used to peel off the Const constructor:

unConst :: Const c a -> c
unConst (Const x) = x

Of course, in practice length is defined as:

length :: [a] -> Int

which effectively hides the fact that it’s a natural transformation.

Finding a parametrically polymorphic function from a Const functor is a little harder, since it would require the creation of a value from nothing. The best we can do is:

scam :: Const Int a -> Maybe a
scam (Const x) = Nothing

Another common functor that we’ve seen already, and which will play an important role in the Yoneda lemma, is the Reader functor. I will rewrite its definition as a newtype:

newtype Reader e a = Reader (e -> a)

It is parameterized by two types, but is (covariantly) functorial only in the second one:

instance Functor (Reader e) where  
    fmap f (Reader g) = Reader (\x -> f (g x))

For every type e, you can define a family of natural transformations from Reader e to any other functor f. We’ll see later that the members of this family are always in one to one correspondence with the elements of f e (the Yoneda lemma).

For instance, consider the somewhat trivial unit type () with one element (). The functor Reader () takes any type a and maps it into a function type ()->a. These are just all the functions that pick a single element from the set a. There are as many of these as there are elements in a. Now let’s consider natural transformations from this functor to the Maybe functor:

alpha :: Reader () a -> Maybe a

There are only two of these, dumb and obvious:

dumb (Reader _) = Nothing

and

obvious (Reader g) = Just (g ())

(The only thing you can do with g is to apply it to the unit value ().)

And, indeed, as predicted by the Yoneda lemma, these correspond to the two elements of the Maybe () type, which are Nothing and Just (). We’ll come back to the Yoneda lemma later — this was just a little teaser.

Beyond Naturality

A parametrically polymorphic function between two functors (including the edge case of the Const functor) is always a natural transformation. Since all standard algebraic data types are functors, any polymorphic function between such types is a natural transformation.

We also have function types at our disposal, and those are functorial in their return type. We can use them to build functors (like the Reader functor) and define natural transformations that are higher-order functions.

However, function types are not covariant in the argument type. They are contravariant. Of course contravariant functors are equivalent to covariant functors from the opposite category. Polymorphic functions between two contravariant functors are still natural transformations in the categorical sense, except that they work on functors from the opposite category to Haskell types.

You might remember the example of a contravariant functor we’ve looked at before:

newtype Op r a = Op (a -> r)

This functor is contravariant in a:

instance Contravariant (Op r) where
    contramap f (Op g) = Op (g . f)

We can write a polymorphic function from, say, Op Bool to Op String:

predToStr (Op f) = Op (\x -> if f x then "T" else "F")

But since the two functors are not covariant, this is not a natural transformation in Hask. However, because they are both contravariant, they satisfy the “opposite” naturality condition:

contramap f . predToStr = predToStr . contramap f

Notice that the function f must go in the opposite direction than what you’d use with fmap, because of the signature of contramap:

contramap :: (b -> a) -> (Op Bool a -> Op Bool b)

Are there any type constructors that are not functors, whether covariant or contravariant? Here’s one example:

a -> a

This is not a functor because the same type a is used both in the negative (contravariant) and positive (covariant) position. You can’t implement fmap or contramap for this type. Therefore a function of the signature:

(a -> a) -> f a

where f is an arbitrary functor, cannot be a natural transformation. Interestingly, there is a generalization of natural transformations, called dinatural transformations, that deals with such cases. We’ll get to them when we discuss ends.

Functor Category

Now that we have mappings between functors — natural transformations — it’s only natural to ask the question whether functors form a category. And indeed they do! There is one category of functors for each pair of categories, C and D. Objects in this category are functors from C to D, and morphisms are natural transformations between those functors.

We have to define composition of two natural transformations, but that’s quite easy. The components of natural transformations are morphisms, and we know how to compose morphisms.

Indeed, let’s take a natural transformation α from functor F to G. Its component at object a is some morphism:

α_a :: F a -> G a

We’d like to compose α with β, which is a natural transformation from functor G to H. The component of β at a is a morphism:

β_a :: G a -> H a

These morphisms are composable and their composition is another morphism:

β_a ∘ α_a :: F a -> H a

We will use this morphism as the component of the natural transformation β ⋅ α — the composition of two natural transformations β after α:

(β ⋅ α)_a = β_a ∘ α_a

One (long) look at a diagram convinces us that the result of this composition is indeed a natural transformation from F to H:

H f ∘ (β ⋅ α)_a = (β ⋅ α)_b ∘ F f

Composition of natural transformations is associative, because their components, which are regular morphisms, are associative with respect to their composition.

Finally, for each functor F there is an identity natural transformation 1_F whose components are the identity morphisms:

id_{F a} :: F a -> F a

So, indeed, functors form a category.

A word about notation. Following Saunders Mac Lane I use the dot for the kind of natural transformation composition I have just described. The problem is that there are two ways of composing natural transformations. This one is called the vertical composition, because the functors are usually stacked up vertically in the diagrams that describe it. Vertical composition is important in defining the functor category. I’ll explain horizontal composition shortly.

The functor category between categories C and D is written as Fun(C, D), or [C, D], or sometimes as D^C. This last notation suggests that a functor category itself might be considered a function object (an exponential) in some other category. Is this indeed the case?

Let’s have a look at the hierarchy of abstractions that we’ve been building so far. We started with a category, which is a collection of objects and morphisms. Categories themselves (or, strictly speaking small categories, whose objects form sets) are themselves objects in a higher-level category Cat. Morphisms in that category are functors. A Hom-set in Cat is a set of functors. For instance Cat(C, D) is a set of functors between two categories C and D.

A functor category [C, D] is also a set of functors between two categories (plus natural transformations as morphisms). Its objects are the same as the members of Cat(C, D). Moreover, a functor category, being a category, must itself be an object of Cat (it so happens that the functor category between two small categories is itself small). We have a relationship between a Hom-set in a category and an object in the same category. The situation is exactly like the exponential object that we’ve seen in the last section. Let’s see how we can construct the latter in Cat.

As you may remember, in order to construct an exponential, we need to first define a product. In Cat, this turns out to be relatively easy, because small categories are sets of objects, and we know how to define cartesian products of sets. So an object in a product category C × D is just a pair of objects, (c, d), one from C and one from D. Similarly, a morphism between two such pairs, (c, d) and (c', d'), is a pair of morphisms, (f, g), where f :: c -> c' and g :: d -> d'. These pairs of morphisms compose component-wise, and there is always an identity pair that is just a pair of identity morphisms. To make the long story short, Cat is a full-blown cartesian closed category in which there is an exponential object D^C for any pair of categories. And by “object” in Cat I mean a category, so D^C is a category, which we can identify with the functor category between C and D.

2-Categories

With that out of the way, let’s have a closer look at Cat. By definition, any Hom-set in Cat is a set of functors. But, as we have seen, functors between two objects have a richer structure than just a set. They form a category, with natural transformations acting as morphisms. Since functors are considered morphisms in Cat, natural transformations are morphisms between morphisms.

This richer structure is an example of a 2-category, a generalization of a category where, besides objects and morphisms (which might be called 1-morphisms in this context), there are also 2-morphisms, which are morphisms between morphisms.

In the case of Cat seen as a 2-category we have:

Objects: (Small) categories
1-morphisms: Functors between categories
2-morphisms: Natural transformations between functors.

Instead of a Hom-set between two categories C and D, we have a Hom-category — the functor category D^C. We have regular functor composition: a functor F from D^C composes with a functor G from E^D to give G ∘ F from E^C. But we also have composition inside each Hom-category — vertical composition of natural transformations, or 2-morphisms, between functors.

With two kinds of composition in a 2-category, the question arises: How do they interact with each other?

Let’s pick two functors, or 1-morphisms, in Cat:

F :: C -> D
G :: D -> E

and their composition:

G ∘ F :: C -> E

Suppose we have two natural transformations, α and β, that act, respectively, on functors F and G:

α :: F -> F'
β :: G -> G'

Notice that we cannot apply vertical composition to this pair, because the target of α is different from the source of β. In fact they are members of two different functor categories: D ^C and E ^D. We can, however, apply composition to the functors F’ and G’, because the target of F’ is the source of G’ — it’s the category D. What’s the relation between the functors G’∘ F’ and G ∘ F?

Having α and β at our disposal, can we define a natural transformation from G ∘ F to G’∘ F’? Let me sketch the construction.

As usual, we start with an object a in C. Its image splits into two objects in D: F a and F'a. There is also a morphism, a component of α, connecting these two objects:

α_a :: F a -> F'a

When going from D to E, these two objects split further into four objects:

G (F a), G'(F a), G (F'a), G'(F'a)

We also have four morphisms forming a square. Two of these morphisms are the components of the natural transformation β:

β_{F a} :: G (F a) -> G'(F a)
β_F'a :: G (F'a) -> G'(F'a)

The other two are the images of α_a under the two functors (functors map morphisms):

G α_a :: G (F a) -> G (F'a)
G'α_a :: G'(F a) -> G'(F'a)

That’s a lot of morphisms. Our goal is to find a morphism that goes from G (F a) to G'(F'a), a candidate for the component of a natural transformation connecting the two functors G ∘ F and G’∘ F’. In fact there’s not one but two paths we can take from G (F a) to G'(F'a):

G'α_a ∘ β_{F a}
β_F'a ∘ G α_a

Luckily for us, they are equal, because the square we have formed turns out to be the naturality square for β.

We have just defined a component of a natural transformation from G ∘ F to G’∘ F’. The proof of naturality for this transformation is pretty straightforward, provided you have enough patience.

We call this natural transformation the horizontal composition of α and β:

β ∘ α :: G ∘ F -> G'∘ F'

Again, following Mac Lane I use the small circle for horizontal composition, although you may also encounter star in its place.

Here’s a categorical rule of thumb: Every time you have composition, you should look for a category. We have vertical composition of natural transformations, and it’s part of the functor category. But what about the horizontal composition? What category does that live in?

The way to figure this out is to look at Cat sideways. Look at natural transformations not as arrows between functors but as arrows between categories. A natural transformation sits between two categories, the ones that are connected by the functors it transforms. We can think of it as connecting these two categories.

Let’s focus on two objects of Cat — categories C and D. There is a set of natural transformations that go between functors that connect C to D. These natural transformations are our new arrows from C to D. By the same token, there are natural transformations going between functors that connect D to E, which we can treat as new arrows going from D to E. Horizontal composition is the composition of these arrows.

We also have an identity arrow going from C to C. It’s the identity natural transformation that maps the identity functor on C to itself. Notice that the identity for horizontal composition is also the identity for vertical composition, but not vice versa.

Finally, the two compositions satisfy the interchange law:

(β' ⋅ α') ∘ (β ⋅ α) = (β' ∘ β) ⋅ (α' ∘ α)

I will quote Saunders Mac Lane here: The reader may enjoy writing down the evident diagrams needed to prove this fact.

There is one more piece of notation that might come in handy in the future. In this new sideways interpretation of Cat there are two ways of getting from object to object: using a functor or using a natural transformation. We can, however, re-interpret the functor arrow as a special kind of natural transformation: the identity natural transformation acting on this functor. So you’ll often see this notation:

F ∘ α

where F is a functor from D to E, and α is a natural transformation between two functors going from C to D. Since you can’t compose a functor with a natural transformation, this is interpreted as a horizontal composition of the identity natural transformation 1_F after α.

Similarly:

α ∘ F

is a horizontal composition of α after 1_F.

Conclusion

This concludes the first part of the book. We’ve learned the basic vocabulary of category theory. You may think of objects and categories as nouns; and morphisms, functors, and natural transformations as verbs. Morphisms connect objects, functors connect categories, natural transformations connect functors.

But we’ve also seen that, what appears as an action at one level of abstraction, becomes an object at the next level. A set of morphisms turns into a function object. As an object, it can be a source or a target of another morphism. That’s the idea behind higher order functions.

A functor maps objects to objects, so we can use it as a type constructor, or a parametric type. A functor also maps morphisms, so it is a higher order function — fmap. There are some simple functors, like Const, product, and coproduct, that can be used to generate a large variety of algebraic data types. Function types are also functorial, both covariant and contravariant, and can be used to extend algebraic data types.

Functors may be looked upon as objects in the functor category. As such, they become sources and targets of morphisms: natural transformations. A natural transformation is a special type of polymorphic function.

Challenges

Define a natural transformation from the Maybe functor to the list functor. Prove the naturality condition for it.
Define at least two different natural transformations between Reader () and the list functor. How many different lists of () are there?
Continue the previous exercise with Reader Bool and Maybe.
Show that horizontal composition of natural transformation satisfies the naturality condition (hint: use components). It’s a good exercise in diagram chasing.
Write a short essay about how you may enjoy writing down the evident diagrams needed to prove the interchange law.
Create a few test cases for the opposite naturality condition of transformations between different Op functors. Here’s one choice:
```
op :: Op Bool Int
op = Op (\x -> x > 0)
```
and
```
f :: String -> Int
f x = read x
```

Next: Declarative Programming.

Acknowledgments

I’d like to thank Gershom Bazerman for checking my math and logic, and André van Meulebrouck, who has been volunteering his editing help.
Follow @BartoszMilewski

March 13, 2015

Function Types

Posted by Bartosz Milewski under Category Theory, Functional Programming, Haskell, Type System
[28] Comments

This is part 9 of Categories for Programmers. Previously: Functoriality. See the Table of Contents.

So far I’ve been glossing over the meaning of function types. A function type is different from other types.

Take Integer, for instance: It’s just a set of integers. Bool is a two element set. But a function type a->b is more than that: it’s a set of morphisms between objects a and b. A set of morphisms between two objects in any category is called a hom-set. It just so happens that in the category Set every hom-set is itself an object in the same category —because it is, after all, a set.

Hom-set in Set is just a set

The same is not true of other categories where hom-sets are external to a category. They are even called external hom-sets.

Hom-set in category C is an external set

It’s the self-referential nature of the category Set that makes function types special. But there is a way, at least in some categories, to construct objects that represent hom-sets. Such objects are called internal hom-sets.

Universal Construction

Let’s forget for a moment that function types are sets and try to construct a function type, or more generally, an internal hom-set, from scratch. As usual, we’ll take our cues from the Set category, but carefully avoid using any properties of sets, so that the construction will automatically work for other categories.

A function type may be considered a composite type because of its relationship to the argument type and the result type. We’ve already seen the constructions of composite types — those that involved relationships between objects. We used universal constructions to define a product type and a coproduct types. We can use the same trick to define a function type. We will need a pattern that involves three objects: the function type that we are constructing, the argument type, and the result type.

The obvious pattern that connects these three types is called function application or evaluation. Given a candidate for a function type, let’s call it z (notice that, if we are not in the category Set, this is just an object like any other object), and the argument type a (an object), the application maps this pair to the result type b (an object). We have three objects, two of them fixed (the ones representing the argument type and the result type).

We also have the application, which is a mapping. How do we incorporate this mapping into our pattern? If we were allowed to look inside objects, we could pair a function f (an element of z) with an argument x (an element of a) and map it to f x (the application of f to x, which is an element of b).

In Set we can pick a function f from a set of functions z and we can pick an argument x from the set (type) a. We get an element f x in the set (type) b.

But instead of dealing with individual pairs (f, x), we can as well talk about the whole product of the function type z and the argument type a. The product z×a is an object, and we can pick, as our application morphism, an arrow g from that object to b. In Set, g would be the function that maps every pair (f, x) to f x.

So that’s the pattern: a product of two objects z and a connected to another object b by a morphism g.

A pattern of objects and morphisms that is the starting point of the universal construction

Is this pattern specific enough to single out the function type using a universal construction? Not in every category. But in the categories of interest to us it is. And another question: Would it be possible to define a function object without first defining a product? There are categories in which there is no product, or there isn’t a product for all pairs of objects. The answer is no: there is no function type, if there is no product type. We’ll come back to this later when we talk about exponentials.

Let’s review the universal construction. We start with a pattern of objects and morphisms. That’s our imprecise query, and it usually yields lots and lots of hits. In particular, in Set, pretty much everything is connected to everything. We can take any object z, form its product with a, and there’s going to be a function from it to b (except when b is an empty set).

That’s when we apply our secret weapon: ranking. This is usually done by requiring that there be a mapping between candidate objects — a mapping that somehow factorizes our construction. In our case, we’ll decree that z together with the morphism g from z×a to b is better than some other z' with its own application g', if and only if there is a mapping h from z' to z such that the application of g' factors through the application of g. (Hint: Read this sentence while looking at the picture.)

Establishing a ranking between candidates for the function object

Now here’s the tricky part, and the main reason I postponed this particular universal construction till now. Given the morphism h :: z'-> z, we want to close the diagram that has both z' and z crossed with a. What we really need, given the mapping h from z' to z, is a mapping from z'×a to z×a. And now, after discussing the functoriality of the product, we know how to do it. Because the product itself is a functor (more precisely an endo-bi-functor), it’s possible to lift pairs of morphisms. In other words, we can define not only products of objects but also products of morphisms.

Since we are not touching the second component of the product z'×a, we will lift the pair of morphisms (h, id), where id is an identity on a.

So, here’s how we can factor one application, g, out of another application g':

g' = g ∘ (h × id)

The key here is the action of the product on morphisms.

The third part of the universal construction is selecting the object that is universally the best. Let’s call this object a⇒b (think of this as a symbolic name for one object, not to be confused with a Haskell typeclass constraint — I’ll discuss different ways of naming it later). This object comes with its own application — a morphism from (a⇒b)×a to b — which we will call eval. The object a⇒b is the best if any other candidate for a function object can be uniquely mapped to it in such a way that its application morphism g factorizes through eval. This object is better than any other object according to our ranking.

The definition of the universal function object. This is the same diagram as above, but now the object a⇒b is universal.

Formally:

A function object from a to b is an object a⇒b together with the morphism

eval :: ((a⇒b) × a) -> b

such that for any other object z with a morphism

g :: z × a -> b

there is a unique morphism

h :: z -> (a⇒b)

that factors g through eval:

g = eval ∘ (h × id)

Of course, there is no guarantee that such an object a⇒b exists for any pair of objects a and b in a given category. But it always does in Set. Moreover, in Set, this object is isomorphic to the hom-set Set(a, b).

This is why, in Haskell, we interpret the function type a->b as the categorical function object a⇒b.

Currying

Let’s have a second look at all the candidates for the function object. This time, however, let’s think of the morphism g as a function of two variables, z and a.

g :: z × a -> b

Being a morphism from a product comes as close as it gets to being a function of two variables. In particular, in Set, g is a function from pairs of values, one from the set z and one from the set a.

On the other hand, the universal property tells us that for each such g there is a unique morphism h that maps z to a function object a⇒b.

h :: z -> (a⇒b)

In Set, this just means that h is a function that takes one variable of type z and returns a function from a to b. That makes h a higher order function. Therefore the universal construction establishes a one-to-one correspondence between functions of two variables and functions of one variable returning functions. This correspondence is called currying, and h is called the curried version of g.

This correspondence is one-to-one, because given any g there is a unique h, and given any h you can always recreate the two-argument function g using the formula:

g = eval ∘ (h × id)

The function g can be called the uncurried version of h.

Currying is essentially built into the syntax of Haskell. A function returning a function:

a -> (b -> c)

is often thought of as a function of two variables. That’s how we read the un-parenthesized signature:

a -> b -> c

This interpretation is apparent in the way we define multi-argument functions. For instance:

catstr :: String -> String -> String
catstr s s’ = s ++ s’

The same function can be written as a one-argument function returning a function — a lambda:

catstr’ s = \s’ -> s ++ s’

These two definitions are equivalent, and either can be partially applied to just one argument, producing a one-argument function, as in:

greet :: String -> String
greet = catstr “Hello “

Strictly speaking, a function of two variables is one that takes a pair (a product type):

(a, b) -> c

It’s trivial to convert between the two representations, and the two (higher-order) functions that do it are called, unsurprisingly, curry and uncurry:

curry :: ((a, b)->c) -> (a->b->c)
curry f a b = f (a, b)

and

uncurry :: (a->b->c) -> ((a, b)->c)
uncurry f (a, b) = f a b

Notice that curry is the factorizer for the universal construction of the function object. This is especially apparent if it’s rewritten in this form:

factorizer :: ((a, b)->c) -> (a->(b->c))
factorizer g = \a -> (\b -> g (a, b))

(As a reminder: A factorizer produces the factorizing function from a candidate.)

In non-functional languages, like C++, currying is possible but nontrivial. You can think of multi-argument functions in C++ as corresponding to Haskell functions taking tuples (although, to confuse things even more, in C++ you can define functions that take an explicit std::tuple, as well as variadic functions, and functions taking initializer lists).

You can partially apply a C++ function using the template std::bind. For instance, given a function of two strings:

std::string catstr(std::string s1, std::string s2) {
    return s1 + s2;
}

you can define a function of one string:

using namespace std::placeholders;

auto greet = std::bind(catstr, "Hello ", _1);
std::cout << greet("Haskell Curry");

Scala, which is more functional than C++ or Java, falls somewhere in between. If you anticipate that the function you’re defining will be partially applied, you define it with multiple argument lists:

def catstr(s1: String)(s2: String) = s1 + s2

Of course that requires some amount of foresight or prescience on the part of a library writer.

Exponentials

In mathematical literature, the function object, or the internal hom-object between two objects a and b, is often called the exponential and denoted by b^a. Notice that the argument type is in the exponent. This notation might seem strange at first, but it makes perfect sense if you think of the relationship between functions and products. We’ve already seen that we have to use the product in the universal construction of the internal hom-object, but the connection goes deeper than that.

This is best seen when you consider functions between finite types — types that have a finite number of values, like Bool, Char, or even Int or Double. Such functions, at least in principle, can be fully memoized or turned into data structures to be looked up. And this is the essence of the equivalence between functions, which are morphisms, and function types, which are objects.

For instance a (pure) function from Bool is completely specified by a pair of values: one corresponding to False, and one corresponding to True. The set of all possible functions from Bool to, say, Int is the set of all pairs of Ints. This is the same as the product Int × Int or, being a little creative with notation, Int².

For another example, let’s look at the C++ type char, which contains 256 values (Haskell Char is larger, because Haskell uses Unicode). There are several functions in the part of the C++ Standard Library that are usually implemented using lookups. Functions like isupper or isspace are implemented using tables, which are equivalent to tuples of 256 Boolean values. A tuple is a product type, so we are dealing with products of 256 Booleans: bool × bool × bool × ... × bool. We know from arithmetics that an iterated product defines a power. If you “multiply” bool by itself 256 (or char) times, you get bool to the power of char, or bool^char.

How many values are there in the type defined as 256-tuples of bool? Exactly 2²⁵⁶. This is also the number of different functions from char to bool, each function corresponding to a unique 256-tuple. You can similarly calculate that the number of functions from bool to char is 256², and so on. The exponential notation for function types makes perfect sense in these cases.

We probably wouldn’t want to fully memoize a function from int or double. But the equivalence between functions and data types, if not always practical, is there. There are also infinite types, for instance lists, strings, or trees. Eager memoization of functions from those types would require infinite storage. But Haskell is a lazy language, so the boundary between lazily evaluated (infinite) data structures and functions is fuzzy. This function vs. data duality explains the identification of Haskell’s function type with the categorical exponential object — which corresponds more to our idea of data.

Cartesian Closed Categories

Although I will continue using the category of sets as a model for types and functions, it’s worth mentioning that there is a larger family of categories that can be used for that purpose. These categories are called cartesian closed, and Set is just one example of such a category.

A cartesian closed category must contain:

The terminal object,
A product of any pair of objects, and
An exponential for any pair of objects.

If you consider an exponential as an iterated product (possibly infinitely many times), then you can think of a cartesian closed category as one supporting products of an arbitrary arity. In particular, the terminal object can be thought of as a product of zero objects — or the zero-th power of an object.

What’s interesting about cartesian closed categories from the perspective of computer science is that they provide models for the simply typed lambda calculus, which forms the basis of all typed programming languages.

The terminal object and the product have their duals: the initial object and the coproduct. A cartesian closed category that also supports those two, and in which product can be distributed over coproduct

a × (b + c) = a × b + a × c
(b + c) × a = b × a + c × a

is called a bicartesian closed category. We’ll see in the next section that bicartesian closed categories, of which Set is a prime example, have some interesting properties.

Exponentials and Algebraic Data Types

The interpretation of function types as exponentials fits very well into the scheme of algebraic data types. It turns out that all the basic identities from high-school algebra relating numbers zero and one, sums, products, and exponentials hold pretty much unchanged in any bicartesian closed category theory for, respectively, initial and final objects, coproducts, products, and exponentials. We don’t have the tools yet to prove them (such as adjunctions or the Yoneda lemma), but I’ll list them here nevertheless as a source of valuable intuitions.

Zeroth Power

a⁰ = 1

In the categorical interpretation, we replace 0 with the initial object, 1 with the final object, and equality with isomorphism. The exponential is the internal hom-object. This particular exponential represents the set of morphisms going from the initial object to an arbitrary object a. By the definition of the initial object, there is exactly one such morphism, so the hom-set C(0, a) is a singleton set. A singleton set is the terminal object in Set, so this identity trivially works in Set. What we are saying is that it works in any bicartesian closed category.

In Haskell, we replace 0 with Void; 1 with the unit type (); and the exponential with function type. The claim is that the set of functions from Void to any type a is equivalent to the unit type — which is a singleton. In other words, there is only one function Void->a. We’ve seen this function before: it’s called absurd.

This is a little bit tricky, for two reasons. One is that in Haskell we don’t really have uninhabited types — every type contains the “result of a never ending calculation,” or the bottom. The second reason is that all implementations of absurd are equivalent because, no matter what they do, nobody can ever execute them. There is no value that can be passed to absurd. (And if you manage to pass it a never ending calculation, it will never return!)

Powers of One

1^a = 1

This identity, when interpreted in Set, restates the definition of the terminal object: There is a unique morphism from any object to the terminal object. In general, the internal hom-object from a to the terminal object is isomorphic to the terminal object itself.

In Haskell, there is only one function from any type a to unit. We’ve seen this function before — it’s called unit. You can also think of it as the function const partially applied to ().

First Power

a¹ = a

This is a restatement of the observation that morphisms from the terminal object can be used to pick “elements” of the object a. The set of such morphisms is isomorphic to the object itself. In Set, and in Haskell, the isomorphism is between elements of the set a and functions that pick those elements, ()->a.

Exponentials of Sums

a^b+c = a^b × a^c

Categorically, this says that the exponential from a coproduct of two objects is isomorphic to a product of two exponentials. In Haskell, this algebraic identity has a very practical, interpretation. It tells us that a function from a sum of two types is equivalent to a pair of functions from individual types. This is just the case analysis that we use when defining functions on sums. Instead of writing one function definition with a case statement, we usually split it into two (or more) functions dealing with each type constructor separately. For instance, take a function from the sum type (Either Int Double):

f :: Either Int Double -> String

It may be defined as a pair of functions from, respectively, Int and Double:

f (Left n)  = if n < 0 then "Negative int" else "Positive int"
f (Right x) = if x < 0.0 then "Negative double" else "Positive double"

Here, n is an Int and x is a Double.

Exponentials of Exponentials

(a^b)^c = a^b×c

This is just a way of expressing currying purely in terms of exponential objects. A function returning a function is equivalent to a function from a product (a two-argument function).

Exponentials over Products

(a × b)^c = a^c × b^c

In Haskell: A function returning a pair is equivalent to a pair of functions, each producing one element of the pair.

It’s pretty incredible how those simple high-school algebraic identities can be lifted to category theory and have practical application in functional programming.

Curry-Howard Isomorphism

I have already mentioned the correspondence between logic and algebraic data types. The Void type and the unit type () correspond to false and true. Product types and sum types correspond to logical conjunction ∧ (AND) and disjunction ⋁ (OR). In this scheme, the function type we have just defined corresponds to logical implication ⇒. In other words, the type a->b can be read as “if a then b.”

According to the Curry-Howard isomorphism, every type can be interpreted as a proposition — a statement or a judgment that may be true or false. Such a proposition is considered true if the type is inhabited and false if it isn’t. In particular, a logical implication is true if the function type corresponding to it is inhabited, which means that there exists a function of that type. An implementation of a function is therefore a proof of a theorem. Writing programs is equivalent to proving theorems. Let’s see a few examples.

Let’s take the function eval we have introduced in the definition of the function object. Its signature is:

eval :: ((a -> b), a) -> b

It takes a pair consisting of a function and its argument and produces a result of the appropriate type. It’s the Haskell implementation of the morphism:

eval :: (a⇒b) × a -> b

which defines the function type a⇒b (or the exponential object b^a). Let’s translate this signature to a logical predicate using the Curry-Howard isomorphism:

((a ⇒ b) ∧ a) ⇒ b

Here’s how you can read this statement: If it’s true that b follows from a, and a is true, then b must be true. This makes perfect intuitive sense and has been known since antiquity as modus ponens. We can prove this theorem by implementing the function:

eval :: ((a -> b), a) -> b
eval (f, x) = f x

If you give me a pair consisting of a function f taking a and returning b, and a concrete value x of type a, I can produce a concrete value of type b by simply applying the function f to x. By implementing this function I have just shown that the type ((a -> b), a) -> b is inhabited. Therefore modus ponens is true in our logic.

How about a predicate that is blatantly false? For instance: if a or b is true then a must be true.

a ⋁ b ⇒ a

This is obviously wrong because you can chose an a that is false and a b that is true, and that’s a counter-example.

Mapping this predicate into a function signature using the Curry-Howard isomorphism, we get:

Either a b -> a

Try as you may, you can’t implement this function — you can’t produce a value of type a if you are called with the Right value. (Remember, we are talking about pure functions.)

Finally, we come to the meaning of the absurd function:

absurd :: Void -> a

Considering that Void translates into false, we get:

 false ⇒ a

Anything follows from falsehood (ex falso quodlibet). Here’s one possible proof (implementation) of this statement (function) in Haskell:

absurd (Void a) = absurd a

where Void is defined as:

newtype Void = Void Void

As always, the type Void is tricky. This definition makes it impossible to construct a value because in order to construct one, you would need to provide one. Therefore, the function absurd can never be called.

These are all interesting examples, but is there a practical side to Curry-Howard isomorphism? Probably not in everyday programming. But there are programming languages like Agda or Coq, which take advantage of the Curry-Howard isomorphism to prove theorems.

Computers are not only helping mathematicians do their work — they are revolutionizing the very foundations of mathematics. The latest hot research topic in that area is called Homotopy Type Theory, and is an outgrowth of type theory. It’s full of Booleans, integers, products and coproducts, function types, and so on. And, as if to dispel any doubts, the theory is being formulated in Coq and Agda. Computers are revolutionizing the world in more than one way.

Bibliography

Ralph Hinze, Daniel W. H. James, Reason Isomorphically!. This paper contains proofs of all those high-school algebraic identities in category theory that I mentioned in this chapter.

Next: Natural Transformations.

Acknowledgments

I’d like to thank Gershom Bazerman for checking my math and logic, and André van Meulebrouck, who has been volunteering his editing help throughout this series of posts.
Follow @BartoszMilewski

« Previous Page — Next Page »