Yes, it’s this time of the year again! I started a little tradition a year ago with Stalking a Hylomorphism in the Wild. This year I was reminded of the Advent of Code by a tweet with this succint C++ program:

This piece of code is probably unreadable to a regular C++ programmer, but makes perfect sense to a Haskell programmer.
Here’s the description of the problem: You are given a list of equal-length strings. Every string is different, but two of these strings differ only by one character. Find these two strings and return their matching part. For instance, if the two strings were “abcd” and “abxd”, you would return “abd”.
What makes this problem particularly interesting is its potential application to a much more practical task of matching strands of DNA while looking for mutations. I decided to explore the problem a little beyond the brute force approach. And, of course, I had a hunch that I might encounter my favorite wild beast–the hylomorphism.
Brute force approach
First things first. Let’s do the boring stuff: read the file and split it into lines, which are the strings we are supposed to process. So here it is:
main = do
txt <- readFile "day2.txt"
let cs = lines txt
print $ findMatch cs
The real work is done by the function findMatch, which takes a list of strings and produces the answer, which is a single string.
findMatch :: [String] -> String
First, let’s define a function that calculates the distance between any two strings.
distance :: (String, String) -> Int
We’ll define the distance as the count of mismatched characters.
Here’s the idea: We have to compare strings (which, let me remind you, are of equal length) character by character. Strings are lists of characters. The first step is to take two strings and zip them together, producing a list of pairs of characters. In fact we can combine the zipping with the next operation–in this case, comparison for inequality, (/=)–using the library function zipWith. However, zipWith is defined to act on two lists, and we will want it to act on a pair of lists–a subtle distinction, which can be easily overcome by applying uncurry:
uncurry :: (a -> b -> c) -> ((a, b) -> c)
which turns a function of two arguments into a function that takes a pair. Here’s how we use it:
uncurry (zipWith (/=))
The comparison operator (/=) produces a Boolean result, True or False. We want to count the number of differences, so we’ll covert True to one, and False to zero:
fromBool :: Num a => Bool -> a
fromBool False = 0
fromBool True = 1
(Notice that such subtleties as the difference between Bool and Int are blisfully ignored in C++.)
Finally, we’ll sum all the ones using sum. Altogether we have:
distance = sum . fmap fromBool . uncurry (zipWith (/=))
Now that we know how to find the distance between any two strings, we’ll just apply it to all possible pairs of strings. To generate all pairs, we’ll use list comprehension:
let ps = [(s1, s2) | s1 <- ss, s2 <- ss]
(In C++ code, this was done by cartesian_product.)
Our goal is to find the pair whose distance is exactly one. To this end, we’ll apply the appropriate filter:
filter ((== 1) . distance) ps
For our purposes, we’ll assume that there is exactly one such pair (if there isn’t one, we are willing to let the program fail with a fatal exception).
(s, s') = head $ filter ((== 1) . distance) ps
The final step is to remove the mismatched character:
filter (uncurry (==)) $ zip s s'
We use our friend uncurry again, because the equality operator (==) expects two arguments, and we are calling it with a pair of arguments. The result of filtering is a list of identical pairs. We’ll fmap fst to pick the first components.
findMatch :: [String] -> String
findMatch ss =
let ps = [(s1, s2) | s1 <- ss, s2 <- ss]
(s, s') = head $ filter ((== 1) . distance) ps
in fmap fst $ filter (uncurry (==)) $ zip s s'
This program produces the correct result and we could stop right here. But that wouldn’t be much fun, would it? Besides, it’s possible that other algorithms could perform better, or be more flexible when applied to a more general problem.
Data-driven approach
The main problem with our brute-force approach is that we are comparing everything with everything. As we increase the number of input strings, the number of comparisons grows like a factorial. There is a standard way of cutting down on the number of comparison: organizing the input into a neat data structure.
We are comparing strings, which are lists of characters, and list comparison is done recursively. Assume that you know that two strings share a prefix. Compare the next character. If it’s equal in both strings, recurse. If it’s not, we have a single character fault. The rest of the two strings must now match perfectly to be considered a solution. So the best data structure for this kind of algorithm should batch together strings with equal prefixes. Such a data structure is called a prefix tree, or a trie (pronounced try).
At every level of our prefix tree we’ll branch based on the current character (so the maximum branching factor is, in our case, 26). We’ll record the character, the count of strings that share the prefix that led us there, and the child trie storing all the suffixes.
data Trie = Trie [(Char, Int, Trie)]
deriving (Show, Eq)
Here’s an example of a trie that stores just two strings, “abcd” and “abxd”. It branches after b.
a 2
b 2
c 1 x 1
d 1 d 1
When inserting a string into a trie, we recurse both on the characters of the string and the list of branches. When we find a branch with the matching character, we increment its count and insert the rest of the string into its child trie. If we run out of branches, we create a new one based on the current character, give it the count one, and the child trie with the rest of the string:
insertS :: Trie -> String -> Trie
insertS t "" = t
insertS (Trie bs) s = Trie (inS bs s)
where
inS ((x, n, t) : bs) (c : cs) =
if c == x
then (c, n + 1, insertS t cs) : bs
else (x, n, t) : inS bs (c : cs)
inS [] (c : cs) = [(c, 1, insertS (Trie []) cs)]
We convert our input to a trie by inserting all the strings into an (initially empty) trie:
mkTrie :: [String] -> Trie
mkTrie = foldl insertS (Trie [])
Of course, there are many optimizations we could use, if we were to run this algorithm on big data. For instance, we could compress the branches as is done in radix trees, or we could sort the branches alphabetically. I won’t do it here.
I won’t pretend that this implementation is simple and elegant. And it will get even worse before it gets better. The problem is that we are dealing explicitly with recursion in multiple dimensions. We recurse over the input string, the list of branches at each node, as well as the child trie. That’s a lot of recursion to keep track of–all at once.
Now brace yourself: We have to traverse the trie starting from the root. At every branch we check the prefix count: if it’s greater than one, we have more than one string going down, so we recurse into the child trie. But there is also another possibility: we can allow to have a mismatch at the current level. The current characters may be different but, since we allow only one mismatch, the rest of the strings have to match exactly. That’s what the function exact does. Notice that exact t is used inside foldMap, which is a version of fold that works on monoids–here, on strings.
match1 :: Trie -> [String]
match1 (Trie bs) = go bs
where
go :: [(Char, Int, Trie)] -> [String]
go ((x, n, t) : bs) =
let a1s = if n > 1
then fmap (x:) $ match1 t
else []
a2s = foldMap (exact t) bs
a3s = go bs -- recurse over list
in a1s ++ a2s ++ a3s
go [] = []
exact t (_, _, t') = matchAll t t'
Here’s the function that finds all exact matches between two tries. It does it by generating all pairs of branches in which top characters match, and then recursing down.
matchAll :: Trie -> Trie -> [String]
matchAll (Trie bs) (Trie bs') = mAll bs bs'
where
mAll :: [(Char, Int, Trie)] -> [(Char, Int, Trie)] -> [String]
mAll [] [] = [""]
mAll bs bs' =
let ps = [ (c, t, t')
| (c, _, t) <- bs
, (c', _', t') <- bs'
, c == c']
in foldMap go ps
go (c, t, t') = fmap (c:) (matchAll t t')
When mAll reaches the leaves of the trie, it returns a singleton list containing an empty string. Subsequent actions of fmap (c:) will prepend characters to this string.
Since we are expecting exactly one solution to the problem, we’ll extract it using head:
findMatch1 :: [String] -> String
findMatch1 cs = head $ match1 (mkTrie cs)
Recursion schemes
As you hone your functional programming skills, you realize that explicit recursion is to be avoided at all cost. There is a small number of recursive patterns that have been codified, and they can be used to solve the majority of recursion problems (for some categorical background, see F-Algebras). Recursion itself can be expressed in Haskell as a data structure: a fixed point of a functor:
newtype Fix f = In { out :: f (Fix f) }
In particular, our trie can be generated from the following functor:
data TrieF a = TrieF [(Char, a)]
deriving (Show, Functor)
Notice how I have replaced the recursive call to the Trie type constructor with the free type variable a. The functor in question defines the structure of a single node, leaving holes marked by the occurrences of a for the recursion. When these holes are filled with full blown tries, as in the definition of the fixed point, we recover the complete trie.
I have also made one more simplification by getting rid of the Int in every node. This is because, in the recursion scheme I’m going to use, the folding of the trie proceeds bottom-up, rather than top-down, so the multiplicity information can be passed upwards.
The main advantage of recursion schemes is that they let us use simpler, non-recursive building blocks such as algebras and coalgebras. Let’s start with a simple coalgebra that lets us build a trie from a list of strings. A coalgebra is a fancy name for a particular type of function:
type Coalgebra f x = x -> f x
Think of x as a type for a seed from which one can grow a tree. A colagebra tells us how to use this seed to create a single node described by the functor f and populate it with (presumably smaller) seeds. We can then pass this coalgebra to a simple algorithm, which will recursively expand the seeds. This algorithm is called the anamorphism:
ana :: Functor f => Coalgebra f a -> a -> Fix f
ana coa = In . fmap (ana coa) . coa
Let’s see how we can apply it to the task of building a trie. The seed in our case is a list of strings (as per the definition of our problem, we’ll assume they are all equal length). We start by grouping these strings into bunches of strings that start with the same character. There is a library function called groupWith that does exactly that. We have to import the right library:
import GHC.Exts (groupWith)
This is the signature of the function:
groupWith :: Ord b => (a -> b) -> [a] -> [[a]]
It takes a function a -> b that converts each list element to a type that supports comparison (as per the typeclass Ord), and partitions the input into lists that compare equal under this particular ordering. In our case, we are going to extract the first character from a string using head and bunch together all strings that share that first character.
let sss = groupWith head ss
The tails of those strings will serve as seeds for the next tier of the trie. Eventually the strings will be shortened to nothing, triggering the end of recursion.
fromList :: Coalgebra TrieF [String]
fromList ss =
-- are strings empty? (checking one is enough)
if null (head ss)
then TrieF [] -- leaf
else
let sss = groupWith head ss
in TrieF $ fmap mkBranch sss
The function mkBranch takes a bunch of strings sharing the same first character and creates a branch seeded with the suffixes of those strings.
mkBranch :: [String] -> (Char, [String])
mkBranch sss =
let c = head (head sss) -- they're all the same
in (c, fmap tail sss)
Notice that we have completely avoided explicit recursion.
The next step is a little harder. We have to fold the trie. Again, all we have to define is a step that folds a single node whose children have already been folded. This step is defined by an algebra:
type Algebra f x = f x -> x
Just as the type x described the seed in a coalgebra, here it describes the accumulator–the result of the folding of a recursive data structure.
We pass this algebra to a special algorithm called a catamorphism that takes care of the recursion:
cata :: Functor f => Algebra f a -> Fix f -> a
cata alg = alg . fmap (cata alg) . out
Notice that the folding proceeds from the bottom up: the algebra assumes that all the children have already been folded.
The hardest part of designing an algebra is figuring out what information needs to be passed up in the accumulator. We obviously need to return the final result which, in our case, is the list of strings with one mismatched character. But when we are in the middle of a trie, we have to keep in mind that the mismatch may still happen above us. So we also need a list of strings that may serve as suffixes when the mismatch occurs. We have to keep them all, because they might be matched later with strings from other branches.
In other words, we need to be accumulating two lists of strings. The first list accumulates all suffixes for future matching, the second accumulates the results: strings with one mismatch (after the mismatch has been removed). We therefore should implement the following algebra:
Algebra TrieF ([String], [String])
To understand the implementation of this algebra, consider a single node in a trie. It’s a list of branches, or pairs, whose first component is the current character, and the second a pair of lists of strings–the result of folding a child trie. The first list contains all the suffixes gathered from lower levels of the trie. The second list contains partial results: strings that were matched modulo single-character defect.
As an example, suppose that you have a node with two branches:
[ ('a', (["bcd", "efg"], ["pq"]))
, ('x', (["bcd"], []))]
First we prepend the current character to strings in both lists using the function prep with the following signature:
prep :: (Char, ([String], [String])) -> ([String], [String])
This way we convert each branch to a pair of lists.
[ (["abcd", "aefg"], ["apq"])
, (["xbcd"], [])]
We then merge all the lists of suffixes and, separately, all the lists of partial results, across all branches. In the example above, we concatenate the lists in the two columns.
(["abcd", "aefg", "xbcd"], ["apq"])
Now we have to construct new partial results. To do this, we create another list of accumulated strings from all branches (this time without prefixing them):
ss = concat $ fmap (fst . snd) bs
In our case, this would be the list:
["bcd", "efg", "bcd"]
To detect duplicate strings, we’ll insert them into a multiset, which we’ll implement as a map. We need to import the appropriate library:
import qualified Data.Map as M
and define a multiset Counts as:
type Counts a = M.Map a Int
Every time we add a new item, we increment the count:
add :: Ord a => Counts a -> a -> Counts a
add cs c = M.insertWith (+) c 1 cs
To insert all strings from a list, we use a fold:
mset = foldl add M.empty ss
We are only interested in items that have multiplicity greater than one. We can filter them and extract their keys:
dups = M.keys $ M.filter (> 1) mset
Here’s the complete algebra:
accum :: Algebra TrieF ([String], [String])
accum (TrieF []) = ([""], [])
accum (TrieF bs) = -- b :: (Char, ([String], [String]))
let -- prepend chars to string in both lists
pss = unzip $ fmap prep bs
(ss1, ss2) = both concat pss
-- find duplicates
ss = concat $ fmap (fst . snd) bs
mset = foldl add M.empty ss
dups = M.keys $ M.filter (> 1) mset
in (ss1, dups ++ ss2)
where
prep :: (Char, ([String], [String])) -> ([String], [String])
prep (c, pss) = both (fmap (c:)) pss
I used a handy helper function that applies a function to both components of a pair:
both :: (a -> b) -> (a, a) -> (b, b)
both f (x, y) = (f x, f y)
And now for the grand finale: Since we create the trie using an anamorphism only to immediately fold it using a catamorphism, why don’t we cut the middle person? Indeed, there is an algorithm called the hylomorphism that does just that. It takes the algebra, the coalgebra, and the seed, and returns the fully charged accumulator.
hylo :: Functor f => Algebra f a -> Coalgebra f b -> b -> a
hylo alg coa = alg . fmap (hylo alg coa) . coa
And this is how we extract and print the final result:
print $ head $ snd $ hylo accum fromList cs
Conclusion
The advantage of using the hylomorphism is that, because of Haskell’s laziness, the trie is never wholly constructed, and therefore doesn’t require large amounts of memory. At every step enough of the data structure is created as is needed for immediate computation; then it is promptly released. In fact, the definition of the data structure is only there to guide the steps of the algorithm. We use a data structure as a control structure. Since data structures are much easier to visualize and debug than control structures, it’s almost always advantageous to use them to drive computation.
In fact, you may notice that, in the very last step of the computation, our accumulator recreates the original list of strings (actually, because of laziness, they are never fully reconstructed, but that’s not the point). In reality, the characters in the strings are never copied–the whole algorithm is just a choreographed dance of internal pointers, or iterators. But that’s exactly what happens in the original C++ algorithm. We just use a higher level of abstraction to describe this dance.
I haven’t looked at the performance of various implementations. Feel free to test it and report the results. The code is available on github.
Acknowledgments
I’m grateful to the participants of the Seattle Haskell Users’ Group for many helpful comments during my presentation.
I wanted to do category theory, not geometry, so the idea of studying simplexes didn’t seem very attractive at first. But as I was getting deeper into it, a very different picture emerged. Granted, the study of simplexes originated in geometry, but then category theorists took interest in it and turned it into something completely different. The idea is that simplexes define a very peculiar scheme for composing things. The way you compose lower dimensional simplexes in order to build higher dimensional simplexes forms a pattern that shows up in totally unrelated areas of mathematics… and programming. Recently I had a discussion with Edward Kmett in which he hinted at the simplicial structure of cumulative edits in a source file.
Geometric picture
Let’s start with a simple idea, and see what we can do with it. The idea is that of triangulation, and it almost goes back to the beginning of the Agricultural Era. Somebody smart noticed long time ago that we can measure plots of land by subdividing them into triangles.
Why triangles and not, say, rectangles or quadrilaterals? Well, to begin with, a quadrilateral can be always divided into triangles, so triangles are more fundamental as units of composition in 2-d. But, more importantly, triangles also work when you embed them in higher dimensions, and quadrilaterals don’t. You can take any three points and there is a unique flat triangle that they span (it may be degenerate, if the points are collinear). But four points will, in general, span a warped quadrilateral. Mind you, rectangles work great on flat screens, and we use them all the time for selecting things with the mouse. But on a curved or bumpy surface, triangles are the only option.
Surveyors have covered the whole Earth, mountains and all, with triangles. In computer games, we build complex models, including human faces or dolphins, using wireframes. Wireframes are just systems of triangles that share some of the vertices and edges. So triangles can be used to approximate complex 2-d surfaces in 3-d.

More dimensions
How can we generalize this process? First of all, we could use triangles in spaces that have more than 3 dimensions. This way we could, for instance, build a Klein bottle in 4-d without it intersecting itself.

We can also consider replacing triangles with higher-dimensional objects. For instance, we could approximate 3-d volumes by filling them with cubes. This technique is used in computer graphics, where we often organize lots of cubes in data structures called octrees. But just like squares or quadrilaterals don’t work very well on non-flat surfaces, cubes cannot be used in curved spaces. The natural generalization of a triangle to something that can fill a volume without any warping is a tetrahedron. Any four points in space span a tetrahedron.

We can go on generalizing this construction to higher and higher dimensions. To form an n-dimensional simplex we can pick 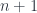 points. We can draw a segment between any two points, a triangle between any three points, a tetrahedron between any four points, and so on. It’s thus natural to define a 1-dimensional simplex to be a segment, and a 0-dimensional simplex to be a point.
points. We can draw a segment between any two points, a triangle between any three points, a tetrahedron between any four points, and so on. It’s thus natural to define a 1-dimensional simplex to be a segment, and a 0-dimensional simplex to be a point.
Simplexes (or simplices, as they are sometimes called) have very regular recursive structure. An n-dimensional simplex has 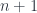 faces, which are all
faces, which are all  dimensional simplexes. A tetrahedron has four triangular faces, a triangle has three sides (one-dimensional simplexes), and a segment has two endpoints. (A point should have one face–and it does, in the “augmented” theory). Every higher-dimensional simplex can be decomposed into lower-dimensional simplexes, and the process can be repeated until we get down to individual vertexes. This constitutes a very interesting composition scheme that will come up over and over again in unexpected places.
dimensional simplexes. A tetrahedron has four triangular faces, a triangle has three sides (one-dimensional simplexes), and a segment has two endpoints. (A point should have one face–and it does, in the “augmented” theory). Every higher-dimensional simplex can be decomposed into lower-dimensional simplexes, and the process can be repeated until we get down to individual vertexes. This constitutes a very interesting composition scheme that will come up over and over again in unexpected places.
Notice that you can always construct a face of a simplex by deleting one point. It’s the point opposite to the face in question. This is why there are as many faces as there are points in a simplex.

Look Ma! No coordinates!
So far we’ve been secretly thinking of points as elements of some n-dimensional linear space, presumably  . Time to make another leap of abstraction. Let’s abandon coordinate systems. Can we still define simplexes and, if so, how would we use them?
. Time to make another leap of abstraction. Let’s abandon coordinate systems. Can we still define simplexes and, if so, how would we use them?
Consider a wireframe built from triangles. It defines a particular shape. We can deform this shape any way we want but, as long as we don’t break connections or fuse points, we cannot change its topology. A wireframe corresponding to a torus can never be deformed into a wireframe corresponding to a sphere.
The information about topology is encoded in connections. The connections don’t depend on coordinates. Two points are either connected or not. Two triangles either share a side or they don’t. Two tetrahedrons either share a triangle or they don’t. So if we can define simplexes without resorting to coordinates, we’ll have a new language to talk about topology.
But what becomes of a point if we discard its coordinates? It becomes an element of a set. An arrangement of simplexes can be built from a set of points or 0-simplexes, together with a set of 1-simplexes, a set of 2-simplexes, and so on. Imagine that you bought a piece of furniture from Ikea. There is a bag of screws (0-simplexes), a box of sticks (1-simplexes), a crate of triangular planks (2-simplexes), and so on. All parts are freely stretchable (we don’t care about sizes).
You have no idea what the piece of furniture will look like unless you have an instruction booklet. The booklet tells you how to arrange things: which sticks form the edges of which triangles, etc. In general, you want to know which lower-order simplexes are the “faces” of higher-order simplexes. This can be determined by defining functions between the corresponding sets, which we’ll call face maps.
For instance, there should be two function from the set of segments to the set of points; one assigning the beginning, and the other the end, to each segment. There should be three functions from the set of triangles to the set of segments, and so on. If the same point is the end of one segment and the beginning of another, the two segments are connected. A segment may be shared between multiple triangles, a triangle may be shared between tetrahedrons, and so on.
You can compose these functions–for instance, to select a vertex of a triangle, or a side of a tetrahedron. Composable functions suggest a category, in this case a subcategory of Set. Selecting a subcategory suggests a functor from some other, simpler, category. What would that category be?
The Simplicial category
The objects of this simpler category, let’s call it the simplicial category 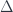 , would be mapped by our functor to corresponding sets of simplexes in Set. So, in
, would be mapped by our functor to corresponding sets of simplexes in Set. So, in 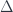 , we need one object corresponding to the set of points, let’s call it
, we need one object corresponding to the set of points, let’s call it ![[0]](https://s0.wp.com/latex.php?latex=%5B0%5D&bg=ffffff&fg=29303b&s=0&c=20201002) ; another for segments,
; another for segments, ![[1]](https://s0.wp.com/latex.php?latex=%5B1%5D&bg=ffffff&fg=29303b&s=0&c=20201002) ; another for triangles,
; another for triangles, ![[2]](https://s0.wp.com/latex.php?latex=%5B2%5D&bg=ffffff&fg=29303b&s=0&c=20201002) ; and so on. In other words, we need one object called
; and so on. In other words, we need one object called ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=29303b&s=0&c=20201002) per one set of n-dimensional simplexes.
per one set of n-dimensional simplexes.

What really determines the structure of this category is its morphisms. In particular, we need morphisms that would be mapped, under our functor, to the functions that define faces of our simplexes–the face maps. This means, in particular, that for every 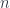 we need
we need 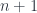 distinct functions from the image of
distinct functions from the image of ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=29303b&s=0&c=20201002) to the image of
to the image of ![[n-1]](https://s0.wp.com/latex.php?latex=%5Bn-1%5D&bg=ffffff&fg=29303b&s=0&c=20201002) . These functions are themselves images of morphisms that go between
. These functions are themselves images of morphisms that go between ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=29303b&s=0&c=20201002) and
and ![[n-1]](https://s0.wp.com/latex.php?latex=%5Bn-1%5D&bg=ffffff&fg=29303b&s=0&c=20201002) in
in 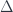 ; we do, however, have a choice of the direction of these morphisms. If we choose our functor to be contravariant, the face maps from the image of
; we do, however, have a choice of the direction of these morphisms. If we choose our functor to be contravariant, the face maps from the image of ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=29303b&s=0&c=20201002) to the image of
to the image of ![[n-1]](https://s0.wp.com/latex.php?latex=%5Bn-1%5D&bg=ffffff&fg=29303b&s=0&c=20201002) will be images of morphisms going from
will be images of morphisms going from ![[n-1]](https://s0.wp.com/latex.php?latex=%5Bn-1%5D&bg=ffffff&fg=29303b&s=0&c=20201002) to
to ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=29303b&s=0&c=20201002) (the opposite direction). This contravariant functor from
(the opposite direction). This contravariant functor from 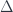 to Set (such functors are called pre-sheaves) is called the simplicial set.
to Set (such functors are called pre-sheaves) is called the simplicial set.
What’s attractive about this idea is that there is a category that has exactly the right types of morphisms. It’s a category whose objects are ordinals, or ordered sets of numbers, and morphisms are order-preserving functions. Object ![[0]](https://s0.wp.com/latex.php?latex=%5B0%5D&bg=ffffff&fg=29303b&s=0&c=20201002) is the one-element set
is the one-element set  ,
, ![[1]](https://s0.wp.com/latex.php?latex=%5B1%5D&bg=ffffff&fg=29303b&s=0&c=20201002) is the set
is the set 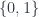 ,
, ![[2]](https://s0.wp.com/latex.php?latex=%5B2%5D&bg=ffffff&fg=29303b&s=0&c=20201002) is
is 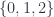 , and so on. Morphisms are functions that preserve order, that is, if
, and so on. Morphisms are functions that preserve order, that is, if 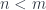 then
then 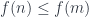 . Notice that the inequality is non-strict. This will become important in the definition of degeneracy maps.
. Notice that the inequality is non-strict. This will become important in the definition of degeneracy maps.
The description of simplicial sets using a functor follows a very common pattern in category theory. The simpler category defines the primitives and the grammar for combining them. The target category (often the category of sets) provides models for the theory in question. The same trick is used, for instance, in defining abstract algebras in Lawvere theories. There, too, the syntactic category consists of a tower of objects with a very regular set of morphisms, and the models are contravariant Set-valued functors.
Because simplicial sets are functors, they form a functor category, with natural transformations as morphisms. A natural transformation between two simplicial sets is a family of functions that map vertices to vertices, edges to edges, triangles to triangles, and so on. In other words, it embeds one simplicial set in another.
Face maps
We will obtain face maps as images of injective morphisms between objects of 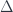 . Consider, for instance, an injection from
. Consider, for instance, an injection from ![[1]](https://s0.wp.com/latex.php?latex=%5B1%5D&bg=ffffff&fg=29303b&s=0&c=20201002) to
to ![[2]](https://s0.wp.com/latex.php?latex=%5B2%5D&bg=ffffff&fg=29303b&s=0&c=20201002) . Such a morphism takes the set
. Such a morphism takes the set 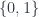 and maps it to
and maps it to 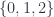 . In doing so, it must skip one of the numbers in the second set, preserving the order of the other two. There are exactly three such morphisms, skipping either
. In doing so, it must skip one of the numbers in the second set, preserving the order of the other two. There are exactly three such morphisms, skipping either 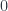 ,
, 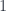 , or
, or 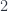 .
.

And, indeed, they correspond to three face maps. If you think of the three numbers as numbering the vertices of a triangle, the three face maps remove the skipped vertex from the triangle leaving the opposing side free. The functor is contravariant, so it reverses the direction of morphisms.

The same procedure works for higher order simplexes. An injection from ![[n-1]](https://s0.wp.com/latex.php?latex=%5Bn-1%5D&bg=ffffff&fg=29303b&s=0&c=20201002) to
to ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=29303b&s=0&c=20201002) maps
maps 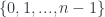 to
to 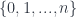 by skipping some
by skipping some 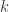 between
between 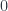 and
and 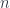 .
.
The corresponding face map is called 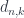 , or simply
, or simply  , if
, if 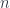 is obvious from the context.
is obvious from the context.
Such face maps automatically satisfy the obvious identities for any  :
:
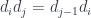
The change from 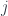 to
to  on the right compensates for the fact that, after removing the
on the right compensates for the fact that, after removing the  th number, the remaining indexes are shifted down.
th number, the remaining indexes are shifted down.
These injections generate, through composition, all the morphisms that strictly preserve the ordering (we also need identity maps to form a category). But, as I mentioned before, we are also interested in those maps that are non-strict in the preservation of ordering (that is, they can map two consecutive numbers into one). These generate the so called degeneracy maps. Before we get to definitions, let me provide some motivation.
Homotopy
One of the important application of simplexes is in homotopy. You don’t need to study algebraic topology to get a feel of what homotopy is. Simply said, homotopy deals with shrinking and holes. For instance, you can always shrink a segment to a point. The intuition is pretty obvious. You have a segment at time zero, and a point at time one, and you can create a continuous “movie” in between. Notice that a segment is a 1-simplex, whereas a point is a 0-simplex. Shrinking therefore provides a bridge between different-dimensional simplexes.

Similarly, you can shrink a triangle to a segment–in particular the segment that is one of its sides.

You can also shrink a triangle to a point by pasting together two shrinking movies–first shrinking the triangle to a segment, and then the segment to a point. So shrinking is composable.
But not all higher-dimensional shapes can be shrunk to all lower-dimensional shapes. For instance, an annulus (a.k.a., a ring) cannot be shrunk to a segment–this would require tearing it. It can, however, be shrunk to a circular loop (or two segments connected end to end to form a loop). That’s because both, the annulus and the circle, have a hole. So continuous shrinking can be used to classify shapes according to how many holes they have.
We have a problem, though: You can’t describe continuous transformations without using coordinates. But we can do the next best thing: We can define degenerate simplexes to bridge the gap between dimensions. For instance, we can build a segment, which uses the same vertex twice. Or a collapsed triangle, which uses the same side twice (its third side is a degenerate segment).
Degeneracy maps
We model operations on simplexes, such as face maps, through morphisms from the category opposite to 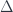 . The creation of degenerate simplexes will therefore corresponds to mappings from
. The creation of degenerate simplexes will therefore corresponds to mappings from ![[n+1]](https://s0.wp.com/latex.php?latex=%5Bn%2B1%5D&bg=ffffff&fg=29303b&s=0&c=20201002) to
to ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=29303b&s=0&c=20201002) . They obviously cannot be injective, but we may chose them to be surjective. For instance, the creation of a degenerate segment from a point corresponds to the (opposite) mapping of
. They obviously cannot be injective, but we may chose them to be surjective. For instance, the creation of a degenerate segment from a point corresponds to the (opposite) mapping of 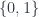 to
to  , which collapses the two numbers to one.
, which collapses the two numbers to one.
We can construct a degenerate triangle from a segment in two ways. These correspond to the two surjections from 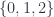 to
to 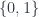 .
.

The first one called 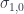 maps both
maps both 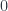 and
and 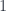 to
to 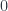 , and
, and 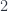 to
to 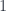 . Notice that, as required, it preserves the order, albeit weakly. The second,
. Notice that, as required, it preserves the order, albeit weakly. The second,  maps
maps 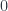 to
to 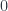 but collapses
but collapses 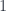 and
and 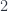 to
to 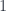 .
.
In general, 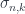 maps
maps 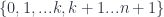 to
to 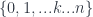 by collapsing
by collapsing 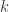 and
and 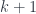 to
to 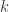 .
.
Our contravariant functor maps these order-preserving surjections to functions on sets. The resulting functions are called degeneracy maps: each 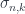 mapped to the corresponding
mapped to the corresponding  . As with face maps, we usually omit the first index, as it’s either arbitrary or easily deducible from the context.
. As with face maps, we usually omit the first index, as it’s either arbitrary or easily deducible from the context.

Two degeneracy maps. In the triangles, two of the sides are actually the same segment. The third side is a degenerate segment whose ends are the same point.
There is an obvious identity for the composition of degeneracy maps:

for 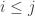 .
.
The interesting identities relate degeneracy maps to face maps. For instance, when 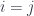 or
or  , we have:
, we have:

(that’s the identity morphism). Geometrically speaking, imagine creating a degenerate triangle from a segment, for instance by using 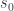 . The first side of this triangle, which is obtained by applying
. The first side of this triangle, which is obtained by applying 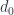 , is the original segment. The second side, obtained by
, is the original segment. The second side, obtained by 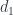 , is the same segment again.
, is the same segment again.
The third side is degenerate: it can be obtained by applying 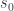 to the vertex obtained by
to the vertex obtained by 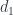 .
.

In general, for  :
:

Similarly:
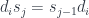
for  .
.
All the face- and degeneracy-map identities are relevant because, given a family of sets and functions that satisfy them, we can reproduce the simplicial set (contravariant functor from 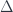 to Set) that generates them. This shows the equivalence of the geometric picture that deals with triangles, segments, faces, etc., with the combinatorial picture that deals with rearrangements of ordered sequences of numbers.
to Set) that generates them. This shows the equivalence of the geometric picture that deals with triangles, segments, faces, etc., with the combinatorial picture that deals with rearrangements of ordered sequences of numbers.
Monoidal structure
A triangle can be constructed by adjoining a point to a segment. Add one more point and you get a tetrahedron. This process of adding points can be extended to adding together arbitrary simplexes. Indeed, there is a binary operator in 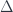 that combines two ordered sequences by stacking one after another.
that combines two ordered sequences by stacking one after another.

This operation can be lifted to morphisms, making it a bifunctor. It is associative, so one might ask the question whether it can be used as a tensor product to make 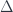 a monoidal category. The only thing missing is the unit object.
a monoidal category. The only thing missing is the unit object.
The lowest dimensional simplex in 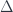 is
is ![[0]](https://s0.wp.com/latex.php?latex=%5B0%5D&bg=ffffff&fg=29303b&s=0&c=20201002) , which represents a point, so it cannot be a unit with respect to our tensor product. Instead we are obliged to add a new object, which is called
, which represents a point, so it cannot be a unit with respect to our tensor product. Instead we are obliged to add a new object, which is called ![[-1]](https://s0.wp.com/latex.php?latex=%5B-1%5D&bg=ffffff&fg=29303b&s=0&c=20201002) , and is represented by an empty set. (Incidentally, this is the object that may serve as “the face” of a point.)
, and is represented by an empty set. (Incidentally, this is the object that may serve as “the face” of a point.)
With the new object ![[-1]](https://s0.wp.com/latex.php?latex=%5B-1%5D&bg=ffffff&fg=29303b&s=0&c=20201002) , we get the category
, we get the category 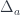 , which is called the augmented simplicial category. Since the unit and associativity laws are satisfied “on the nose” (as opposed to “up to isomorphism”),
, which is called the augmented simplicial category. Since the unit and associativity laws are satisfied “on the nose” (as opposed to “up to isomorphism”), 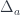 is a strict monoidal category.
is a strict monoidal category.
Note: Some authors prefer to name the objects of 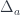 starting from zero, rather than minus one. They rename
starting from zero, rather than minus one. They rename ![[-1]](https://s0.wp.com/latex.php?latex=%5B-1%5D&bg=ffffff&fg=29303b&s=0&c=20201002) to
to 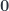 ,
, ![[0]](https://s0.wp.com/latex.php?latex=%5B0%5D&bg=ffffff&fg=29303b&s=0&c=20201002) to
to 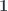 , etc. This convention makes even more sense if you consider that
, etc. This convention makes even more sense if you consider that 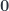 is the initial object and
is the initial object and 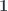 the terminal object in
the terminal object in 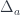 .
.
Monoidal categories are a fertile breeding ground for monoids. Indeed, the object ![[0]](https://s0.wp.com/latex.php?latex=%5B0%5D&bg=ffffff&fg=29303b&s=0&c=20201002) in
in 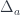 is a monoid. It is equipped with two morphisms that act like unit and multiplication. It has an incoming morphism from the monoidal unit
is a monoid. It is equipped with two morphisms that act like unit and multiplication. It has an incoming morphism from the monoidal unit ![[-1]](https://s0.wp.com/latex.php?latex=%5B-1%5D&bg=ffffff&fg=29303b&s=0&c=20201002) –the morphism that’s the precursor of the face map that assigns the empty set to every point. This morphism can be used as the unit
–the morphism that’s the precursor of the face map that assigns the empty set to every point. This morphism can be used as the unit 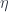 of our monoid. It also has an incoming morphism from
of our monoid. It also has an incoming morphism from ![[1]](https://s0.wp.com/latex.php?latex=%5B1%5D&bg=ffffff&fg=29303b&s=0&c=20201002) (which happens to be the tensorial square of
(which happens to be the tensorial square of ![[0]](https://s0.wp.com/latex.php?latex=%5B0%5D&bg=ffffff&fg=29303b&s=0&c=20201002) ). It’s the precursor of the degeneracy map that creates a segment from a single point. This morphism is the multiplication
). It’s the precursor of the degeneracy map that creates a segment from a single point. This morphism is the multiplication  of our monoid. Unit and associativity laws follow from the standard identities between morphisms in
of our monoid. Unit and associativity laws follow from the standard identities between morphisms in 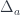 .
.
It turns out that this monoid ![([0], \eta, \mu)](https://s0.wp.com/latex.php?latex=%28%5B0%5D%2C+%5Ceta%2C+%5Cmu%29&bg=ffffff&fg=29303b&s=0&c=20201002) in
in 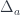 is the mother of all monoids in strict monoidal categories. It can be shown that, for any monoid
is the mother of all monoids in strict monoidal categories. It can be shown that, for any monoid 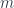 in any strict monoidal category
in any strict monoidal category 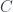 , there is a unique strict monoidal functor
, there is a unique strict monoidal functor  from
from 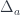 to
to 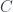 that maps the monoid
that maps the monoid ![[0]](https://s0.wp.com/latex.php?latex=%5B0%5D&bg=ffffff&fg=29303b&s=0&c=20201002) to the monoid
to the monoid 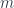 . The category
. The category 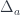 has exactly the right structure, and nothing more, to serve as the pattern for any monoid we can come up within a (strict) monoidal category. In particular, since a monad is just a monoid in the (strictly monoidal) category of endofunctors, the augmented simplicial category is behind every monad as well.
has exactly the right structure, and nothing more, to serve as the pattern for any monoid we can come up within a (strict) monoidal category. In particular, since a monad is just a monoid in the (strictly monoidal) category of endofunctors, the augmented simplicial category is behind every monad as well.
One more thing
Incidentally, since 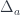 is a monoidal category, (contravariant) functors from it to Set are automatically equipped with monoidal structure via Day convolution. The result of Day convolution is a join of simplicial sets. It’s a generalized cone: two simplicial sets together with all possible connections between them. In particular, if one of the sets is just a single point, the result of the join is an actual cone (or a pyramid).
is a monoidal category, (contravariant) functors from it to Set are automatically equipped with monoidal structure via Day convolution. The result of Day convolution is a join of simplicial sets. It’s a generalized cone: two simplicial sets together with all possible connections between them. In particular, if one of the sets is just a single point, the result of the join is an actual cone (or a pyramid).
Different shapes
If we are willing to let go of geometric interpretations, we can replace the target category of sets with an arbitrary category. Instead of having a set of simplexes, we’ll end up with an object of simplexes. Simplicial sets become simplicial objects.
Alternatively, we can generalize the source category. As I mentioned before, simplexes are a good choice of primitives because of their geometrical properties–they don’t warp. But if we don’t care about embedding these simplexes in  , we can replace them with cubes of varying dimensions (a one dimensional cube is a segment, a two dimensional cube is a square, and so on). Functors from the category of n-cubes to Set are called cubical sets. An even further generalization replaces simplexes with shapeless globes producing globular sets.
, we can replace them with cubes of varying dimensions (a one dimensional cube is a segment, a two dimensional cube is a square, and so on). Functors from the category of n-cubes to Set are called cubical sets. An even further generalization replaces simplexes with shapeless globes producing globular sets.
All these generalizations become important tools in studying higher category theory. In an n-category, we naturally encounter various shapes, as reflected in the naming convention: objects are called 0-cells; morphisms, 1-cells; morphisms between morphisms, 2-cells, and so on. These “cells” are often visualized as n-dimensional shapes. If a 1-cell is an arrow, a 2-cell is a (directed) surface spanning two arrows; a 3-cell, a volume between two surfaces; e.t.c. In this way, the shapeless hom-set that connects two objects in a regular category turns into a topologically rich blob in an n-category.
This is even more pronounced in infinity groupoids, which became popularized by homotopy type theory, where we have an infinite tower of bidirectional n-morphisms. The presence or the absence of higher order morphisms between any two morphisms can be visualized as the existence of holes that prevent the morphing of one cell into another. This kind of morphing can be described by homotopies which, in turn, can be described using simplicial, cubical, globular, or even more exotic sets.
Conclusion
I realize that this post might seem a little rambling. I have two excuses: One is that, when I started looking at simplexes, I had no idea where I would end up. One thing led to another and I was totally fascinated by the journey. The other is the realization how everything is related to everything else in mathematics. You start with simple triangles, you compose and decompose them, you see some structure emerging. Suddenly, the same compositional structure pops up in totally unrelated areas. You see it in algebraic topology, in a monoid in a monoidal category, or in a generalization of a hom-set in an n-category. Why is it so? It seems like there aren’t that many ways of composing things together, and we are forced to keep reusing them over and over again. We can glue them, nail them, or solder them. The way simplicial category is put together provides a template for one of the universal patterns of composition.
Bibliography
-
- John Baez, A Quick Tour of Basic Concepts in Simplicial Homotopy Theory
- Greg Friedman, An elementary illustrated introduction to simplicial sets.
- N J Wildberger, Algebraic Topology. An excellent series of videos.
Acknowledgments
I’m grateful to Edward Kmett and Derek Elkins for reviewing the draft and for providing helpful suggestions.














