Bartosz Milewski's Programming Cafe

This is part 24 of Categories for Programmers. Previously: Comonads. See the Table of Contents.

We’ve seen several formulations of a monoid: as a set, as a single-object category, as an object in a monoidal category. How much more juice can we squeeze out of this simple concept?

Let’s try. Take this definition of a monoid as a set m with a pair of functions:

μ :: m × m -> m
η :: 1 -> m

Here, 1 is the terminal object in Set — the singleton set. The first function defines multiplication (it takes a pair of elements and returns their product), the second selects the unit element from m. Not every choice of two functions with these signatures results in a monoid. For that we need to impose additional conditions: associativity and unit laws. But let’s forget about that for a moment and just consider “potential monoids.” A pair of functions is an element of a cartesian product of two sets of functions. We know that these sets may be represented as exponential objects:

μ ∈ m m×m
η ∈ m1

The cartesian product of these two sets is:

m m×m × m1

Using some high-school algebra (which works in every cartesian closed category), we can rewrite it as:

m m×m + 1

The plus sign stands for the coproduct in Set. We have just replaced a pair of functions with a single function — an element of the set:

m × m + 1 -> m

Any element of this set of functions is a potential monoid.

The beauty of this formulation is that it leads to interesting generalizations. For instance, how would we describe a group using this language? A group is a monoid with one additional function that assigns the inverse to every element. The latter is a function of the type m->m. As an example, integers form a group with addition as a binary operation, zero as the unit, and negation as the inverse. To define a group we would start with a triple of functions:

m × m -> m
m -> m
1 -> m

As before, we can combine all these triples into one set of functions:

m × m + m + 1 -> m

We started with one binary operator (addition), one unary operator (negation), and one nullary operator (identity — here zero). We combined them into one function. All functions with this signature define potential groups.

We can go on like this. For instance, to define a ring, we would add one more binary operator and one nullary operator, and so on. Each time we end up with a function type whose left-hand side is a sum of powers (possibly including the zeroth power — the terminal object), and the right-hand side being the set itself.

Now we can go crazy with generalizations. First of all, we can replace sets with objects and functions with morphisms. We can define n-ary operators as morphisms from n-ary products. It means that we need a category that supports finite products. For nullary operators we require the existence of the terminal object. So we need a cartesian category. In order to combine these operators we need exponentials, so that’s a cartesian closed category. Finally, we need coproducts to complete our algebraic shenanigans.

Alternatively, we can just forget about the way we derived our formulas and concentrate on the final product. The sum of products on the left hand side of our morphism defines an endofunctor. What if we pick an arbitrary endofunctor F instead? In that case we don’t have to impose any constraints on our category. What we obtain is called an F-algebra.

An F-algebra is a triple consisting of an endofunctor F, an object a, and a morphism

F a -> a

The object is often called the carrier, an underlying object or, in the context of programming, the carrier type. The morphism is often called the evaluation function or the structure map. Think of the functor F as forming expressions and the morphism as evaluating them.

Here’s the Haskell definition of an F-algebra:

type Algebra f a = f a -> a

It identifies the algebra with its evaluation function.

In the monoid example, the functor in question is:

data MonF a = MEmpty | MAppend a a

This is Haskell for 1 + a × a (remember algebraic data structures).

A ring would be defined using the following functor:

data RingF a = RZero
             | ROne
             | RAdd a a 
             | RMul a a
             | RNeg a

which is Haskell for 1 + 1 + a × a + a × a + a.

An example of a ring is the set of integers. We can choose Integer as the carrier type and define the evaluation function as:

evalZ :: Algebra RingF Integer
evalZ RZero      = 0
evalZ ROne       = 1
evalZ (RAdd m n) = m + n
evalZ (RMul m n) = m * n
evalZ (RNeg n)   = -n

There are more F-algebras based on the same functor RingF. For instance, polynomials form a ring and so do square matrices.

As you can see, the role of the functor is to generate expressions that can be evaluated using the evaluator of the algebra. So far we’ve only seen very simple expressions. We are often interested in more elaborate expressions that can be defined using recursion.

Recursion

One way to generate arbitrary expression trees is to replace the variable a inside the functor definition with recursion. For instance, an arbitrary expression in a ring is generated by this tree-like data structure:

data Expr = RZero
          | ROne
          | RAdd Expr Expr 
          | RMul Expr Expr
          | RNeg Expr

We can replace the original ring evaluator with its recursive version:

evalZ :: Expr -> Integer
evalZ RZero        = 0
evalZ ROne         = 1
evalZ (RAdd e1 e2) = evalZ e1 + evalZ e2
evalZ (RMul e1 e2) = evalZ e1 * evalZ e2
evalZ (RNeg e)     = -(evalZ e)

This is still not very practical, since we are forced to represent all integers as sums of ones, but it will do in a pinch.

But how can we describe expression trees using the language of F-algebras? We have to somehow formalize the process of replacing the free type variable in the definition of our functor, recursively, with the result of the replacement. Imagine doing this in steps. First, define a depth-one tree as:

type RingF1 a = RingF (RingF a)

We are filling the holes in the definition of RingF with depth-zero trees generated by RingF a. Depth-2 trees are similarly obtained as:

type RingF2 a = RingF (RingF (RingF a))

which we can also write as:

type RingF2 a = RingF (RingF1 a)

Continuing this process, we can write a symbolic equation:

type RingFn+1 a = RingF (RingFn a)

Conceptually, after repeating this process infinitely many times, we end up with our Expr. Notice that Expr does not depend on a. The starting point of our journey doesn’t matter, we always end up in the same place. This is not always true for an arbitrary endofunctor in an arbitrary category, but in the category Set things are nice.

Of course, this is a hand-waving argument, and I’ll make it more rigorous later.

Applying an endofunctor infinitely many times produces a fixed point, an object defined as:

Fix f = f (Fix f)

The intuition behind this definition is that, since we applied f infinitely many times to get Fix f, applying it one more time doesn’t change anything. In Haskell, the definition of a fixed point is:

newtype Fix f = Fix (f (Fix f))

Arguably, this would be more readable if the constructor’s name were different than the name of the type being defined, as in:

newtype Fix f = In (f (Fix f))

but I’ll stick with the accepted notation. The constructor Fix (or In, if you prefer) can be seen as a function:

Fix :: f (Fix f) -> Fix f

There is also a function that peels off one level of functor application:

unFix :: Fix f -> f (Fix f)
unFix (Fix x) = x

The two functions are the inverse of each other. We’ll use these functions later.

Category of F-Algebras

Here’s the oldest trick in the book: Whenever you come up with a way of constructing some new objects, see if they form a category. Not surprisingly, algebras over a given endofunctor F form a category. Objects in that category are algebras — pairs consisting of a carrier object a and a morphism F a -> a, both from the original category C.

To complete the picture, we have to define morphisms in the category of F-algebras. A morphism must map one algebra (a, f) to another algebra (b, g). We’ll define it as a morphism m that maps the carriers — it goes from a to b in the original category. Not any morphism will do: we want it to be compatible with the two evaluators. (We call such a structure-preserving morphism a homomorphism.) Here’s how you define a homomorphism of F-algebras. First, notice that we can lift m to the mapping:

F m :: F a -> F b

we can then follow it with g to get to b. Equivalently, we can use f to go from F a to a and then follow it with m. We want the two paths to be equal:

g ∘ F m = m ∘ f

It’s easy to convince yourself that this is indeed a category (hint: identity morphisms from C work just fine, and a composition of homomorphisms is a homomorphism).

An initial object in the category of F-algebras, if it exists, is called the initial algebra. Let’s call the carrier of this initial algebra i and its evaluator j :: F i -> i. It turns out that j, the evaluator of the initial algebra, is an isomorphism. This result is known as Lambek’s theorem. The proof relies on the definition of the initial object, which requires that there be a unique homomorphism m from it to any other F-algebra. Since m is a homomorphism, the following diagram must commute:

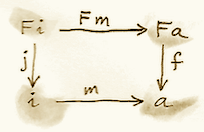
Now let’s construct an algebra whose carrier is F i. The evaluator of such an algebra must be a morphism from F (F i) to F i. We can easily construct such an evaluator simply by lifting j:

F j :: F (F i) -> F i

Because (i, j) is the initial algebra, there must be a unique homomorphism m from it to (F i, F j). The following diagram must commute:

But we also have this trivially commuting diagram (both paths are the same!):

which can be interpreted as showing that j is a homomorphism of algebras, mapping (F i, F j) to (i, j). We can glue these two diagrams together to get:

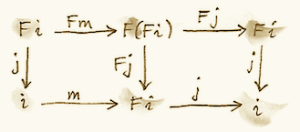
This diagram may, in turn, be interpreted as showing that j ∘ m is a homomorphism of algebras. Only in this case the two algebras are the same. Moreover, because (i, j) is initial, there can only be one homomorphism from it to itself, and that’s the identity morphism idi — which we know is a homomorphism of algebras. Therefore j ∘ m = idi. Using this fact and the commuting property of the left diagram we can prove that m ∘ j = idFi. This shows that m is the inverse of j and therefore j is an isomorphism between F i and i:

F i ≅ i

But that is just saying that i is a fixed point of F. That’s the formal proof behind the original hand-waving argument.

Back to Haskell: We recognize i as our Fix f, j as our constructor Fix, and its inverse as unFix. The isomorphism in Lambek’s theorem tells us that, in order to get the initial algebra, we take the functor f and replace its argument a with Fix f. We also see why the fixed point does not depend on a.

Natural Numbers

Natural numbers can also be defined as an F-algebra. The starting point is the pair of morphisms:

zero :: 1 -> N
succ :: N -> N

The first one picks the zero, and the second one maps all numbers to their successors. As before, we can combine the two into one:

1 + N -> N

The left hand side defines a functor which, in Haskell, can be written like this:

data NatF a = ZeroF | SuccF a

The fixed point of this functor (the initial algebra that it generates) can be encoded in Haskell as:

data Nat = Zero | Succ Nat

A natural number is either zero or a successor of another number. This is known as the Peano representation for natural numbers.

Catamorphisms

Let’s rewrite the initiality condition using Haskell notation. We call the initial algebra Fix f. Its evaluator is the contructor Fix. There is a unique morphism m from the initial algebra to any other algebra over the same functor. Let’s pick an algebra whose carrier is a and the evaluator is alg.

By the way, notice what m is: It’s an evaluator for the fixed point, an evaluator for the whole recursive expression tree. Let’s find a general way of implementing it.

Lambek’s theorem tells us that the constructor Fix is an isomorphism. We called its inverse unFix. We can therefore flip one arrow in this diagram to get:

Let’s write down the commutation condition for this diagram:

m = alg . fmap m . unFix

We can interpret this equation as a recursive definition of m. The recursion is bound to terminate for any finite tree created using the functor f. We can see that by noticing that fmap m operates underneath the top layer of the functor f. In other words, it works on the children of the original tree. The children are always one level shallower than the original tree.

Here’s what happens when we apply m to a tree constructed using Fix f. The action of unFix peels off the constructor, exposing the top level of the tree. We then apply m to all the children of the top node. This produces results of type a. Finally, we combine those results by applying the non-recursive evaluator alg. The key point is that our evaluator alg is a simple non-recursive function.

Since we can do this for any algebra alg, it makes sense to define a higher order function that takes the algebra as a parameter and gives us the function we called m. This higher order function is called a catamorphism:

cata :: Functor f => (f a -> a) -> Fix f -> a
cata alg = alg . fmap (cata alg) . unFix

Let’s see an example of that. Take the functor that defines natural numbers:

data NatF a = ZeroF | SuccF a

Let’s pick (Int, Int) as the carrier type and define our algebra as:

fib :: NatF (Int, Int) -> (Int, Int)
fib ZeroF = (1, 1)
fib (SuccF (m, n)) = (n, m + n)

You can easily convince yourself that the catamorphism for this algebra, cata fib, calculates Fibonacci numbers.

In general, an algebra for NatF defines a recurrence relation: the value of the current element in terms of the previous element. A catamorphism then evaluates the n-th element of that sequence.

Folds

A list of e is the initial algebra of the following functor:

data ListF e a = NilF | ConsF e a

Indeed, replacing the variable a with the result of recursion, which we’ll call List e, we get:

data List e = Nil | Cons e (List e)

An algebra for a list functor picks a particular carrier type and defines a function that does pattern matching on the two constructors. Its value for NilF tells us how to evaluate an empty list, and its value for ConsF tells us how to combine the current element with the previously accumulated value.

For instance, here’s an algebra that can be used to calculate the length of a list (the carrier type is Int):

lenAlg :: ListF e Int -> Int
lenAlg (ConsF e n) = n + 1
lenAlg NilF = 0

Indeed, the resulting catamorphism cata lenAlg calculates the length of a list. Notice that the evaluator is a combination of (1) a function that takes a list element and an accumulator and returns a new accumulator, and (2) a starting value, here zero. The type of the value and the type of the accumulator are given by the carrier type.

Compare this to the traditional Haskell definition:

length = foldr (\e n -> n + 1) 0

The two arguments to foldr are exactly the two components of the algebra.

Let’s try another example:

sumAlg :: ListF Double Double -> Double
sumAlg (ConsF e s) = e + s
sumAlg NilF = 0.0

Again, compare this with:

sum = foldr (\e s -> e + s) 0.0

As you can see, foldr is just a convenient specialization of a catamorphism to lists.

Coalgebras

As usual, we have a dual construction of an F-coagebra, where the direction of the morphism is reversed:

a -> F a

Coalgebras for a given functor also form a category, with homomorphisms preserving the coalgebraic structure. The terminal object (t, u) in that category is called the terminal (or final) coalgebra. For every other algebra (a, f) there is a unique homomorphism m that makes the following diagram commute:

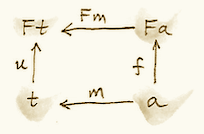
A terminal colagebra is a fixed point of the functor, in the sense that the morphism u :: t -> F t is an isomorphism (Lambek’s theorem for coalgebras):

F t ≅ t

A terminal coalgebra is usually interpreted in programming as a recipe for generating (possibly infinite) data structures or transition systems.

Just like a catamorphism can be used to evaluate an initial algebra, an anamorphism can be used to coevaluate a terminal coalgebra:

ana :: Functor f => (a -> f a) -> a -> Fix f
ana coalg = Fix . fmap (ana coalg) . coalg

A canonical example of a coalgebra is based on a functor whose fixed point is an infinite stream of elements of type e. This is the functor:

data StreamF e a = StreamF e a
  deriving Functor

and this is its fixed point:

data Stream e = Stream e (Stream e)

A coalgebra for StreamF e is a function that takes the seed of type a and produces a pair (StreamF is a fancy name for a pair) consisting of an element and the next seed.

You can easily generate simple examples of coalgebras that produce infinite sequences, like the list of squares, or reciprocals.

A more interesting example is a coalgebra that produces a list of primes. The trick is to use an infinite list as a carrier. Our starting seed will be the list [2..]. The next seed will be the tail of this list with all multiples of 2 removed. It’s a list of odd numbers starting with 3. In the next step, we’ll take the tail of this list and remove all multiples of 3, and so on. You might recognize the makings of the sieve of Eratosthenes. This coalgebra is implemented by the following function:

era :: [Int] -> StreamF Int [Int]
era (p : ns) = StreamF p (filter (notdiv p) ns)
    where notdiv p n = n `mod` p /= 0

The anamorphism for this coalgebra generates the list of primes:

primes = ana era [2..]

A stream is an infinite list, so it should be possible to convert it to a Haskell list. To do that, we can use the same functor StreamF to form an algebra, and we can run a catamorphism over it. For instance, this is a catamorphism that converts a stream to a list:

toListC :: Fix (StreamF e) -> [e]
toListC = cata al
   where al :: StreamF e [e] -> [e]
         al (StreamF e a) = e : a

Here, the same fixed point is simultaneously an initial algebra and a terminal coalgebra for the same endofunctor. It’s not always like this, in an arbitrary category. In general, an endofunctor may have many (or no) fixed points. The initial algebra is the so called least fixed point, and the terminal coalgebra is the greatest fixed point. In Haskell, though, both are defined by the same formula, and they coincide.

The anamorphism for lists is called unfold. To create finite lists, the functor is modified to produce a Maybe pair:

unfoldr :: (b -> Maybe (a, b)) -> b -> [a]

The value of Nothing will terminate the generation of the list.

An interesting case of a coalgebra is related to lenses. A lens can be represented as a pair of a getter and a setter:

set :: a -> s -> a
get :: a -> s

Here, a is usually some product data type with a field of type s. The getter retrieves the value of that field and the setter replaces this field with a new value. These two functions can be combined into one:

a -> (s, s -> a)

We can rewrite this function further as:

a -> Store s a

where we have defined a functor:

data Store s a = Store (s -> a) s

Notice that this is not a simple algebraic functor constructed from sums of products. It involves an exponential as.

A lens is a coalgebra for this functor with the carrier type a. We’ve seen before that Store s is also a comonad. It turns out that a well-behaved lens corresponds to a coalgebra that is compatible with the comonad structure. We’ll talk about this in the next section.

Challenges

1. Implement the evaluation function for a ring of polynomials of one variable. You can represent a polynomial as a list of coefficients in front of powers of x. For instance, 4x2-1 would be represented as (starting with the zero’th power) [-1, 0, 4].
2. Generalize the previous construction to polynomials of many independent variables, like x2y-3y3z.
3. Implement the algebra for the ring of 2×2 matrices.
4. Define a coalgebra whose anamorphism produces a list of squares of natural numbers.
5. Use unfoldr to generate a list of the first n primes.

Next: Algebras for Monads.

If there is one structure that permeates category theory and, by implication, the whole of mathematics, it’s the monoid. To study the evolution of this concept is to study the power of abstraction and the idea of getting more for less, which is at the core of mathematics. When I say “evolution” I don’t necessarily mean chronological development. I’m looking at a monoid as if it were a life form evolving through various eons of abstraction.

It’s an ambitious project and I’ll have to cover a lot of material. I’ll start slowly, with the definitions of magmas and monoids, but then I will accelerate. A lot of concepts will be introduced in one or two sentences, mainly to familiarize the reader with the notation. I’ll dwell a little on monoidal categories, then breeze through ends, coends, and profunctors. I’ll show you how monads, arrows, and applicative functors arise from monoids in various monoidal categories.

The Magmas of the Hadean Eon

Monoids evolved from more primitive life forms feeding on sets. So, before even touching upon monoids, let’s talk about cartesian products, relations, and functions. You take two sets a and b (or, in the simplest case, two copies of the same set a) and form pairs of elements. That gives you a set of pairs, a.k.a., the cartesian product a×b. Any subset of such a cartesian product is called a relation. Two elements x and y are in a relation if the pair <x, y> is a member of that subset.

A function from a to b is a special kind of relation, in which every element x in the set a has one and only one element y in the set b that’s related to it. (Sometimes this is called a total function, since it’s defined for all elements of a).

Even before there were monoids, there was magma. A magma is a set with a binary operation and nothing else. So, in particular, there is no assumption of associativity, and there is no unit. A binary operation is simply a function from the cartesian product of a with itself back to a

a × a -> a

It takes a pair of elements <x, y>, both coming from the set a, and maps it to an element of a.

It’s tempting to quote the Haskell definition of a magma:

class Magma a where
  (<>) :: a -> a -> a

but this definition is already tainted with some higher concepts like currying. An alternative would be:

class Magma a where
  (<>) :: (a, a) -> a

Here, we at least see a pair of elements that are being “multiplied.” But the pair type (a, a) is also a higher-level concept. I’ll come back to it later.

Lack of associativity means that we cannot identify (x<>y)<>z with x<>(y<>z). You have to keep the parentheses.

You might have heard of quaternions — their multiplication is associative. But not many people have heard of octonions, which are not associative. In fact Hamilton, who discovered quaternions, invented the word associative to disassociate himself from octonions, which are not.

If you’re familiar with continuous groups, you might know that Lie algebras are not associative.

Closer to home — most operations on floating-point numbers are not associative on modern computers because of rounding errors.

But, really, most interesting binary operations are associative. So out of the magma emerges a semigroup. In a semigroup you can drop parentheses. A non-trivial (that is, non-monoidal) example of a semigroup is the set of integers with max binary operation. A maximum of three numbers is the same no matter in which order you pair them. But there is no integer that’s less or equal to any other integer, so this is not a monoid.

Monoids of the Archean Eon

But, really, most interesting binary operations are both associative and unital. There usually is a “do nothing” element with respect to most binary operations. So life as we know it begins with a monoid.

A monoid is a set with a binary operation that is associative, and with a special element called the unit e that is neutral with respect to the binary operation. To be precise, these are the three monoid laws:

(x <> y) <> z = x <> (y <> z)
e <> x = x
x <> e = x

In Haskell, the traditional definition of a monoid uses mempty for the unit and mappend for the binary operation:

class Monoid a where
    mempty  :: a
    mappend :: a -> a -> a

As with the magma, the definition of mappend is curried. Equivalently, it could have been written as:

mappend :: (a, a) -> a

I’ll come back to this point later.

There are plenty of examples of monoids. Non-negative integers with addition, or positive integers with multiplication are the obvious ones. Strings with concatenation are interesting too, because concatenation is not commutative.

Just like pairs of elements from two sets a and b organize themselves into a set a×b, which is their cartesian product; functions between two sets organize themselves into a set — the set of functions from a to b, which we sometimes write as a->b.

This organizing principle is characteristic of sets, where everything you can think of is a set. Except when it’s more than just a set — for instance when you try to organize all sets into one large collection. This collection, or “class,” is not itself a set. You can’t have a set of all sets, but you can have a category Set of “small” sets, which are sets that belong to a “universe.” In what follows, I will confine myself to a single universe in order to dodge questions from foundational mathematicians.

Let’s now pop one level up and look at cartesian product as an operation on sets. For any two sets a and b, we can construct the set a×b. If we view this as “multiplication” of sets, we can say that sets form a magma. But do they form a monoid? Not exactly! To begin with, cartesian product is not associative. We can see it in Haskell: the type ((a, b), c) is not the same as the type (a, (b, c)). They are, however, isomorphic. There is an invertible function called the associator, from one type to the other:

alpha :: ((a, b), c) -> (a, (b, c))
alpha ((x, y), z) = (x, (y, z))

It’s just a repackaging of containers (such repackaging is, by the way, called a natural transformation).

For the unit of this “multiplication” we can pick the singleton set. In Haskell, this is the type called unit and it’s denoted by an empty pair of parentheses (). Again, the unit laws are valid up to isomorphism. There are two such isomorphisms called left and right unitors:

lambda :: ((), a) -> a
lambda ((), x) = x
rho :: (a, ()) -> a
rho (x, ()) -> x

We have just exposed monoidal structure in the category Set. Set is not strictly a monoid because monoidal laws are satisfied only up to isomorphism.

There is another monoidal structure in Set. Just like cartesian product resembles multiplication, there is an operation on sets that resembles addition. It’s called disjoint sum. In Haskell it’s embodied in the type Either a b . Just like cartesian product, disjoint sum is associative up to isomorphism. The unit (or the “zero”) of this sum type is the empty set or, in Haskell, the Void type — also up to isomorphism.

The Cambrian Explosion of Categories

The first rule of abstraction is, You do not talk about Fight Club. In the category Set, for instance, we are not supposed to admit that sets have elements. An object in Set is really a set, but you never talk about its elements. We still have functions between sets, but they become abstract morphisms, of which we only know how they compose.

Composition of functions is associative, and there is an identity function for every set, which serves as a unit of composition. We can write these rules compactly as:

(f ∘ g) ∘ h = f ∘ (g ∘ h)
id ∘ f = f
f ∘ id = f

These look exactly like monoid laws. So do functions form a monoid with respect to composition? Not quite, because you can’t compose any two functions. They must be composable, which means their endpoints have to match. In Haskell, we can compose g after f, or g ∘ f, only if:

f :: a -> b
g :: b -> c

Also, there is no single identity function, but a whole family of functions ida, one for each set a. In Haskell, we call that a polymorphic function.

But notice what happens if we restrict ourselves to just a single object a in Set. Every morphism from a back to a can be composed with any other such morphism (their endpoints always match). Moreover, we are guaranteed that among those so called endomorphisms there is one identity morphism ida, which acts as a unit of composition.

Notice that I switched from the set/function nomenclature to the more general object/morphism naming convention of category theory. We can now forget about sets and functions and define an arbitrary category as a collection (a set in a given universe) of objects, and sets of morphisms that go between them. The only requirements are that any two composable morphisms compose, and that there is an identity morphism for every object. And that composition must be associative.

We can now forget about sets and define a monoid as a category that has only one object. The binary operation is just the composition of (endo-)morphisms. It works! We have defined a monoid without a set. Or have we?

No, we haven’t! We have just swept it under the rug — the rug being the set of morphisms. Yes, morphisms between any two objects form a set called the hom-set. In a category C, the hom-set between objects a and b is denoted by C(a, b). So we haven’t completely eliminated sets from the picture.

In the single object category M, we have only one hom-set M(a, a). The elements of this set — and we are allowed to call them elements because it’s a set — are morphisms like f and g. We can compose them, and we can call this composition “multiplication,” thus recovering our previous definition of the monoid as a set. We get associativity for free, and we have the identity morphism ida serving as the unit.

It might seem at first that we haven’t made progress and, in fact, we might have made some things more complicated by forgetting the internal structure of objects. For instance, in the category Set, it’s no longer obvious what an empty set is. You can’t say it’s a set with no elements because of the Fight Club rule. Similarly with the singleton set. Fortunately, it turns out that both these sets can be uniquely described in terms of their interactions with other sets. By that I mean the kind of functions/morphisms that connect them to other objects in Set. These object-opaque definitions are called universal constructions. For instance, the empty set is the only set that has a unique morphism going from it to every other set. The advantage of this characterization is that it can now be applied to any category. One may ask this question in any category: Is there an object that has this property? If there is, we call it the initial object. The empty set is the initial object in Set. Similarly, a singleton set is the terminal object in Set (and it’s unique up to unique isomorphism).

A cartesian product of two sets can also be defined using a universal construction, one which doesn’t mention elements (or pairs of elements). And again, this construction may be used to define a (categorical) product in other categories. Of particular interest are categories where a product exists for every pair of objects (it does in Set).

In such categories there is actually an even better way of defining a product using an adjunction. But before we can get to adjunctions, let me summarize a few millions of years of evolution in a few terse paragraphs.

A functor is a mapping of categories that preserves their structure. It maps objects to objects and morphisms to morphisms. In Haskell we define a functor (really, an endofunctor) as a type constructor f (a mapping from types to types) that can be lifted to functions that go between these types:

class Functor f where
  fmap :: (a -> b) -> (f a -> f b)

The mapping of morphisms must also preserve composition and identity. Functors may collapse multiple objects into one, and multiple morphisms into one, but they never break connections. You may also think of functors as embedding one category inside another.

Finally, functors can be composed in the obvious way, and there is an identity endofunctor that maps a category onto itself. It follows that categories (at least the small ones) form a category Cat in which functors serve as morphisms.

There may be many ways of embedding one category inside another, and it’s extremely useful to be able to compare such embeddings by defining mappings between them. If we have two functors F and G between two categories C and D we define a natural transformation between these functors by picking a morphism between a pair F a and G a, for every a.

In Haskell, a natural transformation between two functors f and g is a polymorphic function:

type Nat f g = forall a. f a -> g a

In general, natural transformations must obey additional naturality conditions, but in Haskell they come for free (due to parametricity).

Natural transformations may be composed, and there is an identity natural transformations from any functor to itself. It follows that functors between any two categories C and D form a category denoted by [C, D], where natural transformations play the role of morphisms. A hom-set in such a category is a set of natural transformations between two functors F and G denoted by [C, D](F, G).

An invertible natural transformation is called a natural isomorphism. If two functors are naturally isomorphic they are essentially the same.

Arthropods and their Adjoints

Using a pair of functors that are the inverse of each other we may define equivalence of categories, but there is an even more useful concept of adjoint functors that compare the structures of two non-equivalent categories. The idea is that we have a “right” functor R going from category C to D and a “left” functor L going in the other direction, from D to C.

There are two possible compositions of these functors, both resulting in round trips or endofunctors. The categories would be equivalent if those endofunctors were naturally isomorphic to identity endofunctors. But for an adjunction, we impose weaker conditions. We require that there be two natural transformations (not necessarily isomorphisms):

η :: ID -> R ∘ L
ε :: L ∘ R -> IC

The first transformation η is called the unit; and the second ε, the counit of the adjunction.

In a small category objects form sets, so it’s possible to form a cartesian product of two small categories C and D. Object in such a category C×D are pairs of objects <c, d>, and morphisms are pairs of morphisms <f, g>.

After these preliminaries, we are ready to define the categorical product in C using an adjunction. We chose C×C as the left category. The left functor is the diagonal functor Δ that maps any object c to a pair <c, c> and any morphism f to a pair of morphisms <f, f>. Its right adjoint, if it exists, maps a pair of objects <a, b> to their categorical product a×b.

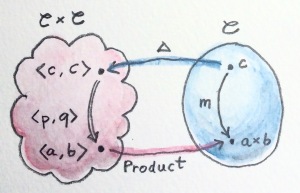
Interestingly, the terminal object can also be defined using an adjunction. This time we chose, as the left category, a singleton category with one object and one (identity) morphism. The left functor maps any object c to the singleton object. Its right adjoint, if it exists, maps the singleton object to the terminal object in C.

A category with all products and the terminal object is called a cartesian category, or cartesian monoidal category. Why monoidal? Because the operation of taking the categorical product is monoidal. It’s associative, up to isomorphism; and its unit is the terminal object.

Incidentally, this is the same monoidal structure that we’ve seen in Set, but now it’s generalized to the level of other categories. There was another monoidal structure in Set induced by the disjoint sum. Its categorical generalization is given by the coproduct, with the initial object playing the role of the unit.

But what about the set of morphisms? In Set, morphisms between two sets a and b form a hom-set, which is the object of the same category Set. In an arbitrary category C, a hom-set C(a, b) is still a set — but now it’s not an object of C. That’s why it’s called the external hom-set. However, there are categories in which each external hom-set has a corresponding object called the internal hom. This object is also called an exponential, ba. It can be defined using an adjunction, but only if the category supports products. It’s an adjunction in which the left and right categories are the same. The left endofunctor takes an object b and maps it to a product b×a, where a is an arbitrary fixed object. Its adjoint functor maps an object b to the exponential ba. The counit of this adjunction:

ε :: ba × a -> b

is the evaluation function. In Haskell it has the following signature:

eval :: (a -> b, a) -> b

The Haskell function type a->b is equivalent to the exponential ba.

A category that has all products and exponentials together with the terminal object is called cartesian closed. Cartesian closed categories, or CCCs, play an important role in the semantics of programming languages.

Tensorosaurus Rex

We have already seen two very similar monoidal structures induced by products and coproducts. In mathematics, two is a crowd, so let’s look for a pattern. Both product and coproduct act as bifunctors C×C->C. Let’s call such a bifunctor a tensor product and write it as an infix operator a ⊗ b. As a bifunctor, the tensor product can also lift pairs of morphisms:

f :: a -> a'
g :: b -> b'
f ⊗ g :: a ⊗ b -> a' ⊗ b'

To define a monoid on top of a tensor product, we will require that it be associative — up to isomorphism:

α :: (a ⊗ b) ⊗ c -> a ⊗ (b ⊗ c)

We also need a unit object, which we will call i. The two unit laws are:

λ :: i ⊗ a -> a
ρ :: a ⊗ i -> a

A category with a tensor product that satisfies the above properties, plus some additional coherence conditions, is called a monoidal category.

We can now specialize the tensor product to categorical product, in which case the unit object is the terminal object; or to coproduct, in which case we chose the initial object as the unit. But there is an even more interesting operation that has all the properties of the tensor product. I’m talking about functor composition.

Functorosaurus

Functors between any two categories C and D form a functor category [C, D] with natural transformations playing the role of morphisms. In general, these functors don’t compose (their endpoints don’t match) unless we pick the target category to be the same as the source category.

Endofunctor Composition

In the endofunctor category [C, C] any two functors can be composed. But in [C, C] functors are objects, so functor composition becomes an operation on objects. For any two endofunctors F and G it produces a new endofunctor F∘G. It’s a binary operation, so it’s a potential candidate for a tensor product. Indeed, it is a bifunctor: it can be lifted to natural transformations, which are morphisms in [C, C]. It’s associative — in fact it’s strictly associative, the associator α is the identity natural transformation. The unit with respect to endofunctor composition is the identity functor I. So the category of endofunctors is a monoidal category.

Unlike product and coproduct, which are symmetric up to isomorphism, endofunctor composition is not symmetric. In general, there is no relation between F∘G and G∘F.

Profunctor Composition

Different species of functors came up with their own composition strategies. Take for instance the profunctors, which are functors Cop×D->Set. They generalize the idea of relations between objects in C and D. The sets they map to may be thought of as sets of proofs of the relationship. An empty set means that the two objects are not related. If you want to compose two relations, you have to find an element that’s common to the image of one relation and the source of the other (relations are not, in general, symmetric). The proofs of the new composite relation are pairs of proofs of individual relations. Symbolically, if p and q are such profunctors/relations, their composition can be written as:

exists x. (p a x, q x b)

Existential quantification in Haskell translates to polymorphic construction, so the actual definition is:

data PCompose p q a b = forall x . PCompose (p a x) (q x b)

In category theory, existential quantification is encoded as the coend, which is a generalization of a colimit for profunctors. The coend formula for the composition of two profunctors reads:

(p ⊗ q) a b = ∫ z p a z × q z b

The product here is the cartesian product of sets.

Profunctors, being functors, form a category in which morphisms are natural transformations. As long as the two categories that they relate are the same, any two profunctors can be composed using a coend. So profunctor composition is a good candidate for a tensor product in such a category. It is indeed associative, up to isomorphism. But what’s the unit of profunctor composition? It turns out that the simplest profuctor — the hom-functor — because of the Yoneda lemma, is the unit of composition:

∫ z C(a, z) × p z b ≅ p a b
∫ z p a z × C(z, b) ≅ p a b

Thus profunctors Cop×C->Set form a monoidal category.

Day Convolution

Or consider Set-valued functors. They can be composed using Day convolution. For that, the category C must itself be monoidal. Day convolution of two functors C->Set is defined using a coend:

(f ★ g) a = ∫ x y f x × g y × C(x ⊗ y, a)

Here, the tensor product of x ⊗ y comes from the monoidal category C, the other products are just cartesian products of sets (one of them being the hom-set).

As before, in Haskell, the coend turns into existential quantifier, which can be written symbolically:

Day f g a = exists x y. ((f x, g y), (x, y) -> a)

and encoded as a polymorphic constructor:

data Day f g a = forall x y. Day (f x) (g y) ((x, y) -> a)

We use the fact that the category of Haskell types is monoidal with respect to cartesian product.

We can build a monoidal category based on Day convolution. The unit with respect to Day convolution is C(i, -), the hom-functor applied to i — the unit in the monoidal category C. For instance, the left identity can be derived from:

(C(i, -) ★ g) a = ∫ x y C(i, x) × g y × C(x ⊗ y, a)

Applying the Yoneda lemma, or “integrating over x,” we get:

∫y g y × C(i ⊗ y, a)

Considering that i is the unit of the tensor product, we can perform the second integration to get g a.

The Monozoic Era

Monoidal categories are important because they provide rich grazing grounds for monoids. In a monoidal category we can define a more general monoid. It’s an object m with some special properties. These properties replace the usual definitions of multiplication and unit.

First, let’s reformulate the definition of a set-based monoid, taking into account the fact that Set is a monoidal category with respect to cartesian product.

A monoid is a set, so it’s an object in Set — let’s call it m. Multiplication maps pairs of elements of m back to m. These pairs are just elements of the cartesian product m × m. So multiplication is defined as a function:

μ :: m × m -> m

Unit of multiplication is a special element of m. We can select this element by providing a special morphism from the singleton set to m:

η :: () -> m

We can now express associativity and unit laws as properties of these two functions. The beauty of this formulation is that it generalizes easily to any cartesian category — just replace functions with morphisms and the unit () with the terminal object. There’s no reason to stop there: we can lift this definition all the way up to a monoidal category.

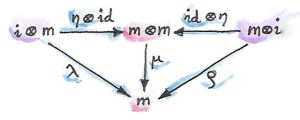
A monoid in a monoidal category is an object m together with two morphisms:

μ :: m ⊗ m -> m
η :: i -> m

Here i is the unit object with respect to the tensor product ⊗. Monoidal laws can be expressed using the associator α and the two unitors, λ and ρ, of the monoidal category:

Having previously defined several interesting monoidal categories, we can now go digging for new monoids.

Monads

Let’s start with the category of endofunctors where the tensor product is functor composition. A monoid in the category of endofunctors is an endofunctor m and two morphism. Remember that morphisms in a functor category are natural transformations. So we end up with two natural transformations:

μ :: m ∘ m -> m
η :: I -> m

where I is the identity functor. Their components at an object a are:

μa :: m (m a) -> m a
ηa :: a -> m a

This construct is easily recognizable as a monad. The associativity and unit laws are just monad laws. In Haskell, μa is called join and ηa is called return.

Arrows

Let’s switch to the category of profunctors Cop×C->Set with profunctor composition as the tensor product. A monoid in that category is a profunctor ar. Multiplication is defined by a natural transformation:

μ :: ar ⊗ ar -> ar

Its component at a, b is:

μa b :: (∫ z ar a z × ar z b) -> ar a b

To simplify this formula we need a very useful identity that relates coends to ends. A hom-set that starts at a coend is equivalent to an end of the hom set:

C(∫ z p z z, y) ≅ ∫ z C(p z z, y)

Or, replacing external hom-sets with internal homs:

(∫ z p z z) -> y ≅ ∫ z (p z z -> y)

In Haskell, this formula is used to turn functions that take existential types to functions that are polymorphic:

(exists z. p z z) -> y ≅ forall z. (p z z -> y)

Intuitively, it makes perfect sense. If you want to define a function that takes an existential type, you have to be prepared to handle any type.

Using that identity, our multiplication formula can be rewritten as:

μa b :: ∫ z ((ar a z × ar z b) -> ar a b)

In Haskell, this derivation uses the existential quantifier:

mu a b = (exists z. (ar a z, ar z b)) -> ar a b

As we discussed, a function from an existential type is equivalent to a polymorphic function:

forall z. (ar a z, ar z b) -> ar a b

or, after currying and dropping the redundant quantification:

ar a z -> ar z b -> ar a b

This looks very much like a composition of morphisms in a category. In Haskell, this function is known in the infix-operator form as:

(>>>) :: ar a z -> ar z b -> ar a b

Let’s see what we get as the monoidal unit. Remember that the unit object in the profunctor category is the hom-functor C(a, b).

ηa b :: C(a, b) -> ar a b

In Haskell, this polymorphic function is traditionally called arr:

arr :: (a -> b) -> ar a b

The whole construct is known in Haskell as a pre-arrow. The full arrow is defined as a monoid in the category of strong profunctors, with strength defined as a natural transformation:

sta b :: p a b -> p (a, x) (b, x)

In Haskell, this function is called first.

Applicatives

There are several categorical formulations of what’s called in Haskell the applicative functor. To first approximaton, Haskell’s type system is the category Set. To translate Haskell constructs to category theory, the safest approach is to just play with endofunctors in Set. But both Set and its endofunctors have a lot of extra structure, so I’d like to start in a slightly more general setting.

Let’s have a look at the monoidal category of functors [C, Set], with Day convolution as the tensor product, and C(i, -) as unit. A monoid in this category is a functor f with multiplication given by the natural transformation:

μ :: f ★ f -> f

and unit given by:

η :: C(i, -) -> f

It turns out that the existence of these two natural transformations is equivalent to the requirement that f be a lax monoidal functor, which is the basis of the definition of the applicative functor in Haskell.

A monoidal functor is a functor that maps monoidal structure of one category to the monoidal structure of another category. It maps the tensor product, and it maps the unit object. In our case, the source category C has the monoidal structure given by the tensor product ⊗, and the target category Set is monoidal with respect to the cartesian product ×. A functor is monoidal if it doesn’t matter whether we first map two object and then multiply them, or first multiply them and then map the result:

f x × f y ≅ f (x ⊗ y)

Also, the unit object in Set should be isomporphic to the result of mapping the unit object in C:

() ≅ f i

Here, () is the terminal object in Set and i is the unit object in C.

These conditions are relaxed in the definition of a lax monoidal functor. A lax monoidal functor replaces isomorphisms with regular unidirectional morphisms:

f x × f y -> f (x ⊗ y)
() -> f i

It can be shown that the monoid in the category[C, Set], with Day convolution as the tensor product, is equivalent to the lax monoidal functor.

The Haskell definition of Applicative doesn’t look like Day convolution or like a lax monoidal functor:

class Functor f => Applicative f where
    (<*>) :: f (a -> b) -> (f a -> f b)
    pure :: a -> f a

You may recognize pure as a component of η, the natural transformation defining the monoid with respect to Day convolution. When you replace the category C with Set, the unit object C(i, -) turns into the identity functor. However, the operator <*> is lifted from the definition of yet another lax functor, the lax closed functor. It’s a functor that preserves the closed structure defined by the internal hom functor. In Set, the internal hom functor is just the arrow (->), hence the definition:

class Functor f => Closed f where
    (<*>) :: f (a -> b) -> (f a -> f b)
    unit :: f ()

As long as the internal hom is defined through the adjunction with the product, a lax closed functor is equivalent to a lax monoidal functor.

Conclusion

It is pretty shocking to realize how many different animals share the same body plan — I’m talking here about the monoid as the skeleton of a myriad of different mathematical and programming constructs. And I haven’t even touched on the whole kingdom of enriched categories, where monoidal categories form the reservoir of hom-objects. Virtually all notions I’ve discussed here can be generalized to enriched categories, including functors, profunctors, the Yoneda lemma, Day convolution, and so on.

Glossary

• Hadean Eon: Began with the formation of the Earth about 4.6 billion years ago. It’s the period before the earliest-known rocks.
• Archean Eon: During the Archean, the Earth’s crust had cooled enough to allow the formation of continents.
• Cambrian explosion: Relatively short evolutionary event, during which most major animal phyla appeared.
• Arthropods: from Greek ἄρθρωσις árthrosis, “joint”
• Tensor, from Latin tendere “to stretch”
• Functor: from Latin fungi, “perform”

Bibliograhpy

1. Moggi, Notions of Computation and Monads.
2. Rivas, Jaskelioff, Notions of Computation as Monoids.

Unlike monads, which came into programming straight from category theory, applicative functors have their origins in programming. McBride and Paterson introduced applicative functors as a programming pearl in their paper Applicative programming with effects. They also provided a categorical interpretation of applicatives in terms of strong lax monoidal functors. It’s been accepted that, just like “a monad is a monoid in the category of endofunctors,” so “an applicative is a strong lax monoidal functor.”

The so called “tensorial strength” seems to be important in categorical semantics, and in his seminal paper Notions of computation and monads, Moggi argued that effects should be described using strong monads. It makes sense, considering that a computation is done in a context, and you should be able to make the global context available under the monad. The fact that we don’t talk much about strong monads in Haskell is due to the fact that all functors in the category Set, which underlies the Haskell’s type system, have canonical strength. So why do we talk about strength when dealing with applicative functors? I have looked into this question and came to the conclusion that there is no fundamental reason, and that it’s okay to just say:

An applicative is a lax monoidal functor

In this post I’ll discuss different equivalent categorical definitions of the applicative functor. I’ll start with a lax closed functor, then move to a lax monoidal functor, and show the equivalence of the two definitions. Then I’ll introduce the calculus of ends and show that the third definition of the applicative functor as a monoid in a suitable functor category equipped with Day convolution is equivalent to the previous ones.

Applicative as a Lax Closed Functor

The standard definition of the applicative functor in Haskell reads:

class Functor f => Applicative f where
    (<*>) :: f (a -> b) -> (f a -> f b)
    pure :: a -> f a

At first sight it doesn’t seem to involve a monoidal structure. It looks more like preserving function arrows (I added some redundant parentheses to suggest this interpretation).

Categorically, functors that “preserve arrows” are known as closed functors. Let’s look at a definition of a closed functor f between two categories C and D. We have to assume that both categories are closed, meaning that they have internal hom-objects for every pair of objects. Internal hom-objects are also called function objects or exponentials. They are normally defined through the right adjoint to the product functor:

C(z × a, b) ≅ C(z, a => b)

To distinguish between sets of morphisms and function objects (they are the same thing in Set), I will temporarily use double arrows for function objects.

We can take a functor f and act with it on the function object a=>b in the category C. We get an object f (a=>b) in D. Or we can map the two objects a and b from C to D and then construct the function object in D: f a => f b.

We call a functor closed if the two results are isomorphic (I have subscripted the two arrows with the categories where they are defined):

f (a =>C b) ≅ (f a =>D f b)

and if the functor preserves the unit object:

iD ≅ f iC

What’s the unit object? Normally, this is the unit with respect to the same product that was used to define the function object using the adjunction. I’m saying “normally,” because it’s possible to define a closed category without a product.

Note: The two arrows and the two is are defined with respect to two different products. The first isomorphism must be natural in both a and b. Also, to complete the picture, there are some diagrams that must commute.

The two isomorphisms that define a closed functor can be relaxed and replaced by unidirectional morphisms. The result is a lax closed functor:

f (a => b) -> (f a => f b)
i -> f i

This looks almost like the definition of Applicative, except for one problem: how can we recover the natural transformation we call pure from a single morphism i -> f i.

One way to do it is from the position of strength. An endofunctor f has tensorial strength if there is a natural transformation:

stc a :: c ⊗ f a -> f (c ⊗ a)

Think of c as the context in which the computation f a is performed. Strength means that we can use this external context inside the computation.

In the category Set, with the tensor product replaced by cartesian product, all functors have canonical strength. In Haskell, we would define it as:

st (c, fa) = fmap ((,) c) fa

The morphism in the definition of the lax closed functor translates to:

unit :: () -> f ()

Notice that, up to isomorphism, the unit type () is the unit with respect to cartesian product. The relevant isomorphisms are:

λa :: ((), a) -> a
ρa :: (a, ()) -> a

Here’s the derivation from Rivas and Jaskelioff’s Notions of Computation as Monoids:

    a
≅  (a, ())   -- unit law, ρ-1
-> (a, f ()) -- lax unit
-> f (a, ()) -- strength
≅  f a       -- lifted unit law, f ρ

Strength is necessary if you’re starting with a lax closed (or monoidal — see the next section) endofunctor in an arbitrary closed (or monoidal) category and you want to derive pure within that category — not after you restrict it to Set.

There is, however, an alternative derivation using the Yoneda lemma:

f ()
≅ forall a. (() -> a) -> f a  -- Yoneda
≅ forall a. a -> f a -- because: (() -> a) ≅ a

We recover the whole natural transformation from a single value. The advantage of this derivation is that it generalizes beyond endofunctors and it doesn’t require strength. As we’ll see later, it also ties nicely with the Day-convolution definition of applicative. The Yoneda lemma only works for Set-valued functors, but so does Day convolution (there are enriched versions of both Yoneda and Day convolution, but I’m not going to discuss them here).

We can define the categorical version of the Haskell’s applicative functor as a lax closed functor going from a closed category C to Set. It’s a functor equipped with a natural transformation:

f (a => b) -> (f a -> f b)

where a=>b is the internal hom-object in C (the second arrow is a function type in Set), and a function:

1 -> f i

where 1 is the singleton set and i is the unit object in C.

The importance of a categorical definition is that it comes with additional identities or “axioms.” A lax closed functor must be compatible with the structure of both categories. I will not go into details here, because we are really only interested in closed categories that are monoidal, where these axioms are easier to express.

The definition of a lax closed functor is easily translated to Haskell:

class Functor f => Closed f where
    (<*>) :: f (a -> b) -> f a -> f b
    unit :: f ()

Applicative as a Lax Monoidal Functor

Even though it’s possible to define a closed category without a monoidal structure, in practice we usually work with monoidal categories. This is reflected in the equivalent definition of the Haskell’s applicative functor as a lax monoidal functor. In Haskell, we would write:

class Functor f => Monoidal f where
    (>*<) :: (f a, f b) -> f (a, b)
    unit :: f ()

This definition is equivalent to our previous definition of a closed functor. That’s because, as we’ve seen, a function object in a monoidal category is defined in terms of a product. We can show the equivalence in a more general categorical setting.

This time let’s start with a symmetric closed monoidal category C, in which the function object is defined through the right adjoint to the tensor product:

C(z ⊗ a, b) ≅ C(z, a => b)

As usual, the tensor product is associative and unital — with the unit object i — up to isomorphism. The symmetry is defined through natural isomorphism:

γ :: a ⊗ b -> b ⊗ a

A functor f between two monoidal categories is lax monoidal if there exist: (1) a natural transformation

f a ⊗ f b -> f (a ⊗ b)

and (2) a morphism

i -> f i

Notice that the products and units on either side of the two mappings are from different categories.

A (lax-) monoidal functor must also preserve associativity and unit laws.

For instance a triple product

f a ⊗ (f b ⊗ f c)

may be rearranged using an associator α to give

(f a ⊗ f b) ⊗ f c

then converted to

f (a ⊗ b) ⊗ f c

and then to

f ((a ⊗ b) ⊗ c)

Or it could be first converted to

f a ⊗ f (b ⊗ c)

and then to

f (a ⊗ (b ⊗ c))

These two should be equivalent under the associator in C.

Similarly, f a ⊗ i can be simplified to f a using the right unitor ρ in D. Or it could be first converted to f a ⊗ f i, then to f (a ⊗ i), and then to f a, using the right unitor in C. The two paths should be equivalent. (Similarly for the left identity.)

We will now consider functors from C to Set, with Set equipped with the usual cartesian product, and the singleton set as unit. A lax monoidal functor is defined by: (1) a natural transformation:

(f a, f b) -> f (a ⊗ b)

and (2) a choice of an element of the set f i (a function from 1 to f i picks an element from that set).

We need the target category to be Set because we want to be able to use the Yoneda lemma to show equivalence with the standard definition of applicative. I’ll come back to this point later.

The Equivalence

The definitions of a lax closed and a lax monoidal functors are equivalent when C is a closed symmetric monoidal category. The proof relies on the existence of the adjunction, in particular the unit and the counit of the adjunction:

ηa :: a -> (b => (a ⊗ b))
εb :: (a => b) ⊗ a -> b

For instance, let’s assume that f is lax-closed. We want to construct the mapping

(f a, f b) -> f (a ⊗ b)

First, we apply the lifted pair (unit, identity), (f η, f id)

(f a -> f (b => a ⊗ b), f id)

to the left hand side. We get:

(f (b => a ⊗ b), f b)

Now we can use (the uncurried version of) the lax-closed morphism:

(f (b => x), f b) -> f x

to get:

f (a ⊗ b)

Conversely, assuming the lax-monoidal property we can show that the functor is lax-closed, that is to say, implement the following function:

(f (a => b), f a) -> f b

First we use the lax monoidal morphism on the left hand side:

f ((a => b) ⊗ a)

and then use the counit (a.k.a. the evaluation morphism) to get the desired result f b

There is yet another presentation of applicatives using Day convolution. But before we get there, we need a little refresher on calculus.

Calculus of Ends

Ends and coends are very useful constructs generalizing limits and colimits. They are defined through universal constructions. They have a few fundamental properties that are used over and over in categorical calculations. I’ll just introduce the notation and a few important identities. We’ll be working in a symmetric monoidal category C with functors from C to Set and profunctors from C^op×C to Set. The end of a profunctor p is a set denoted by:

∫a p a a

The most important thing about ends is that a set of natural transformations between two functors f and g can be represented as an end:

[C, Set](f, g) = ∫a C(f a, g a)

In Haskell, the end corresponds to universal quantification over a functor of mixed variance. For instance, the natural transformation formula takes the familiar form:

forall a. f a -> g a

The Yoneda lemma, which deals with natural transformations, can also be written using an end:

∫z (C(a, z) -> f z) ≅ f a

In Haskell, we can write it as the equivalence:

forall z. ((a -> z) -> f z) ≅ f a

which is a generalization of the continuation passing transform.

The dual notion of coend is similarly written using an integral sign, with the “integration variable” in the superscript position:

∫ a p a a

In pseudo-Haskell, a coend is represented by an existential quantifier. It’s possible to define existential data types in Haskell by converting existential quantification to universal one. The relevant identity in terms of coends and ends reads:

(∫ z p z z) -> y ≅ ∫ z (p z z -> y)

In Haskell, this formula is used to turn functions that take existential types to functions that are polymorphic:

(exists z. p z z) -> y ≅ forall z. (p z z -> y)

Intuitively, it makes perfect sense. If you want to define a function that takes an existential type, you have to be prepared to handle any type.

The equivalent of the Yoneda lemma for coends reads:

∫ z f z × C(z, a) ≅ f a

or, in pseudo-Haskell:

exists z. (f z, z -> a) ≅ f a

(The intuition is that the only thing you can do with this pair is to fmap the function over the first component.)

There is also a contravariant version of this identity:

∫ z C(a, z) × f z ≅ f a

where f is a contravariant functor (a.k.a., a presheaf). In pseudo-Haskell:

exists z. (a -> z, f z) ≅ f a

(The intuition is that the only thing you can do with this pair is to apply the contramap of the first component to the second component.)

Using coends we can define a tensor product in the category of functors [C, Set]. This product is called Day convolution:

(f ★ g) a = ∫ x y f x × g y × C(x ⊗ y, a)

It is a bifunctor in that category (read, it can be used to lift natural transformations). It’s associative and symmetric up to isomorphism. It also has a unit — the hom-functor C(i, -), where i is the monoidal unit in C. In other words, Day convolution imbues the category [C, Set] with monoidal structure.

Let’s verify the unit laws.

(C(i, -) ★ g) a = ∫ x y C(i, x) × g y × C(x ⊗ y, a)

We can use the contravariant Yoneda to “integrate over x” to get:

∫ y g y × C(i ⊗ y, a)

Considering that i is the unit of the tensor product in C, we get:

∫ y g y × C(y, a)

Covariant Yoneda lets us “integrate over y” to get the desired g a. The same method works for the right unit law.

Applicative as a Monoid

Given a monoidal category, we can always define a monoid as an object m equipped with two morphisms:

μ :: m ⊗ m -> m
η :: i -> m

satisfying the laws of associativity and unitality.

We have shown that the functor category [C, Set] (with C a symmetric monoidal category) is monoidal under Day convolution. An object in this category is a functor f. The two morphisms that would make it a candidate for a monoid are natural transformations:

μ :: f ★ f -> f
η :: C(i, -) -> f

The a component of the natural transformation μ can be rewritten as:

(∫ x y f x × f y × C(x ⊗ y, a)) -> f a

which is equivalent to:

∫x y (f x × f y × C(x ⊗ y, a) -> f a)

or, upon currying:

∫x y (f x, f y) -> C(x ⊗ y, a) -> f a

It turns out that so defined monoid is equivalent to a lax monoidal functor. This was shown by Rivas and Jaskelioff. The following derivation is due to Bob Atkey.

The trick is to start with the whole set of natural transformation from f★f to f. The multiplication μ is just one of them. We’ll express the set of natural transformations as an end:

∫ a ((f ★ f) a -> f a)

Plugging in the formula for the a component of μ, we get:

∫ a x y (f x, f y) -> C(x ⊗ y, a) -> f a

The end over a does not involve the first argument, so we can move the integral sign:

∫ x y (f x, f y) -> ∫ a C(x ⊗ y, a) -> f a

Then we use the Yoneda lemma to “perform the integration” over a:

∫ x y (f x, f y) -> f (x ⊗ y)

You may recognize this as a set of natural transformations that define a lax monoidal functor. We have established a one-to-one correspondence between these natural transformations and the ones defining monoidal multiplication using Day convolution.

The remaining part is to show the equivalence between the unit with respect to Day convolution and the second part of the definition of the lax monoidal functor, the morphism:

1 -> f i

We start with the set of natural transformations that contains our η:

∫ a (i -> a) -> f a

By Yoneda, this is just f i. Picking an element from a set is equivalent to defining a morphism from the singleton set 1, so for any choice of η we get:

1 -> f i

and vice versa. The two definitions are equivalent.

Notice that the monoidal unit η under Day convolution becomes the definition of pure in the Haskell version of applicative. Indeed, when we replace the category C with Set, f becomes and endofunctor, and the unit of Day convolution C(i, -) becomes the identity functor Id. We get:

η :: Id -> f

or, in components:

pure :: a -> f a

So, strictly speaking, the Haskell definition of Applicative mixes the elements of the lax closed functor and the monoidal unit under Day convolution.

Acknowledgments

I’m grateful to Mauro Jaskelioff and Exequiel Rivas for correspondence and to Bob Atkey, Dimitri Chikhladze, and Make Shulman for answering my questions on Math Overflow.

I’m a refugee. I fled Communist Poland and was granted political asylum in the United States. That was so long ago that I don’t think of myself as a refugee any more. I’m an American — not by birth but by choice. My understanding is that being an American has nothing to do with ethnicity, religion, or personal history. I became an American by accepting a certain system of values specified in the Constitution. Things like freedom of expression, freedom from persecution, equality, pursuit of happiness, etc. I’m also a Pole and proud of it. I speak the language, I know my history and culture. No contradiction here.

I’m a scientist, and I normally leave politics to others. In fact I came to the United States to get away from politics. In Poland, I was engaged in political struggle, I was a member of Solidarity, and I joined the resistance when Solidarity was crushed. I could have stayed and continued the fight, but I chose instead to leave and make my contribution to society in other areas.

There are times in history when it’s best for scientists to sit in their ivory towers and do what they are trained to do — science. There is time when it’s best for engineers to design new things, write software, and build gadgets that make life easier for everybody. But there are times when this is not enough. That’s why I’m interrupting my scheduled programming, my category theory for programmers blog, to say a few words about current events. Actually, first I’d like to reminisce a little.

When you live under a dictatorship, you have to develop certain skills. If direct approach can get you in trouble, you try to manipulate the system. When martial law was imposed in Poland, all international travel was suspended. I was a grad student then, working on my Ph.D. in theoretical physics. Contact with scientists from abroad was very important to me. As soon as the martial law was suspended, my supervisor and I decided to go for a visit — not to the West, mind you, but to the Soviet Union. But the authorities decided that giving passports to scientists was a great opportunity to make them work for the system. So before we could get a permission to go abroad, we had to visit the Department of Security — the Secret Police — for an interview. From our friends, who were interviewed before, we knew that we’d be offered a choice: become an informant or forget about traveling abroad.

My professor went first. He was on time, but they kept him waiting outside the office forever. After an hour, he stormed out. He didn’t get the passport.

When I went to my interview, it started with some innocuous questions. I was asked who the chief of Solidarity at the University was. That was no secret — he was my office mate in the Physics Department. Then the discussion turned to my future employment at the University. The idea was to suggest that the Department of Security could help me keep my position, or get me fired. Knowing what was coming, I bluffed, saying that I was one of the brightest young physicists around, and my employment was perfectly secure. Then I started talking about my planned trip to the Soviet Union. I took my interviewer into confidence, and explained how horribly the Soviet science is suffering because their government is not allowing their scientists to travel to the West, and how much better Polish science was because of that. You have to realize that, even in the depth of the Department of Security of a Communist country, there was no love for our Soviet brethren. If we could beat them at science, all the better. I got my passport without any more hassle.

I was exaggerating a little, especially about me being so bright, but it’s true that there is an international community of scientists and engineers that knows no borders. Any impediment to free exchange of ideas and people is very detrimental to its prosperity and, by association, to the prosperity of the societies they live in.

I consider the recent Muslim ban — and that’s what it should be called — a direct attack on this community, on a par with climate-change denials and gag orders against climate scientists working for the government. It’s really hard to piss off scientists and engineers, so I consider this a major accomplishment of the new presidency.

You can make fun of us nerds as much as you want, but every time you send a tweet, you’re using the infrastructure created by us. The billions of matal-oxide field-effect transistors and the liquid-crystal display in your tablet were made possible by developments in quantum mechanics and materials science. The operating system was written by software engineers in languages based on the math developed by Alan Turing and Alonzo Church. Try denying that, and you’ll end up tweeting with a quill on parchment.

Scientists and engineers consider themselves servants of the society. We don’t make many demands and are quite happy to be left alone to do our stuff. But if this service is disrupted by clueless, power-hungry politicians, we will act. We are everywhere, and we know how to use the Internet — we invented it.

P. S. I keep comments to my blog under moderation because of spam. But I will also delete comments that I consider clueless.

Here’s a little anecdote about cluelessness that I heard long time ago from my physicist friends in the Soviet Union. They had invited a guest scientist from the US to one of the conferences. They were really worried that he might say something politically charged and make future scientific exchanges impossible. So they asked him to, please, refrain from any political comments.

Time comes for the guest scientist to give a talk. And he starts with, “Before I came to the Soviet Union I was warned that I will be constantly minded by the secret police.” The director of the institute, who invited our scientist, is sitting in the first row between two KGB minders. All blood is leaving his face. The KGB minders stiffen in their seats. “I’m so happy that it turned out to be nonsense,” says the scientist and proceeds to give his talk. You see, it’s really hard to imagine what it’s like to live under dictatorship unless you’ve experienced it yourself. Trust me, I’ve been there and I recognize the warning signs.