Bartosz Milewski's Programming Cafe

This is part 26 of Categories for Programmers. Previously: Algebras for Monads. See the Table of Contents.

There are many intuitions that we may attach to morphisms in a category, but we can all agree that if there is a morphism from the object a to the object b than the two objects are in some way “related.” A morphism is, in a sense, the proof of this relation. This is clearly visible in any poset category, where a morphism is a relation. In general, there may be many “proofs” of the same relation between two objects. These proofs form a set that we call the hom-set. When we vary the objects, we get a mapping from pairs of objects to sets of “proofs.” This mapping is functorial — contravariant in the first argument and covariant in the second. We can look at it as establishing a global relationship between objects in the category. This relationship is described by the hom-functor:

C(-, =) :: Cop × C -> Set

In general, any functor like this may be interpreted as establishing a relation between objects in a category. A relation may also involve two different categories C and D. A functor, which describes such a relation, has the following signature and is called a profunctor:

p :: Dop × C -> Set

Mathematicians say that it’s a profunctor from C to D (notice the inversion), and use a slashed arrow as a symbol for it:

C ↛ D

You may think of a profunctor as a proof-relevant relation between objects of C and objects of D, where the elements of the set symbolize proofs of the relation. Whenever p a b is empty, there is no relation between a and b. Keep in mind that relations don’t have to be symmetric.

Another useful intuition is the generalization of the idea that an endofunctor is a container. A profunctor value of the type p a b could then be considered a container of bs that are keyed by elements of type a. In particular, an element of the hom-profunctor is a function from a to b.

In Haskell, a profunctor is defined as a two-argument type constructor p equipped with the method called dimap, which lifts a pair of functions, the first going in the “wrong” direction:

class Profunctor p where
    dimap :: (c -> a) -> (b -> d) -> p a b -> p c d

The functoriality of the profunctor tells us that if we have a proof that a is related to b, then we get the proof that c is related to d, as long as there is a morphism from c to a and another from b to d. Or, we can think of the first function as translating new keys to the old keys, and the second function as modifying the contents of the container.

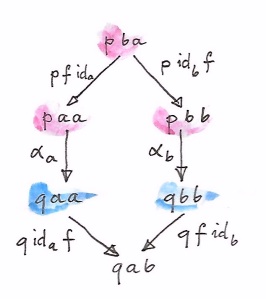
For profunctors acting within one category, we can extract quite a lot of information from diagonal elements of the type p a a. We can prove that b is related to c as long as we have a pair of morphisms b->a and a->c. Even better, we can use a single morphism to reach off-diagonal values. For instance, if we have a morphism f::a->b, we can lift the pair <f, idb> to go from p b b to p a b:

dimap f id pbb :: p a b

Or we can lift the pair <ida, f> to go from p a a to p a b:

dimap id f paa :: p a b

Dinatural Transformations

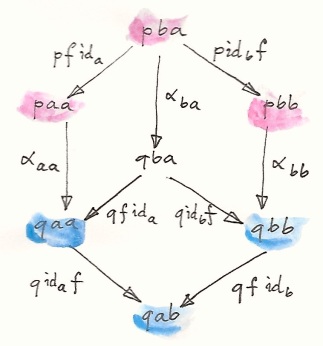
Since profunctors are functors, we can define natural transformations between them in the standard way. In many cases, though, it’s enough to define the mapping between diagonal elements of two profunctors. Such a transformation is called a dinatural transformation, provided it satisfies the commuting conditions that reflect the two ways we can connect diagonal elements to non-diagonal ones. A dinatural transformation between two profunctors p and q, which are members of the functor category [Cop × C, Set], is a family of morphisms:

αa :: p a a -> q a a

for which the following diagram commutes, for any f::a->b:

Notice that this is strictly weaker than the naturality condition. If α were a natural transformation in [Cop × C, Set], the above diagram could be constructed from two naturality squares and one functoriality condition (profunctor q preserving composition):

Notice that a component of a natural transformation α in [Cop × C, Set] is indexed by a pair of objects α a b. A dinatural transformation, on the other hand, is indexed by one object, since it only maps diagonal elements of the respective profunctors.

Ends

We are now ready to advance from “algebra” to what could be considered the “calculus” of category theory. The calculus of ends (and coends) borrows ideas and even some notation from traditional calculus. In particular, the coend may be understood as an infinite sum or an integral, whereas the end is similar to an infinite product. There is even something that resembles the Dirac delta function.

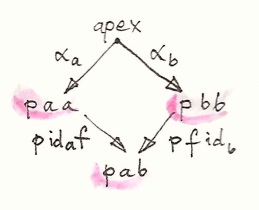
An end is a generalization of a limit, with the functor replaced by a profunctor. Instead of a cone, we have a wedge. The base of a wedge is formed by diagonal elements of a profunctor p. The apex of the wedge is an object (here, a set, since we are considering Set-valued profunctors), and the sides are a family of functions mapping the apex to the sets in the base. You may think of this family as one polymorphic function — a function that’s polymorphic in its return type:

α :: forall a . apex -> p a a

Unlike in cones, within a wedge we don’t have any functions that would connect the vertices that form the base. However, as we’ve seen earlier, given any morphism f::a->b in C, we can connect both p a a and p b b to the common set p a b. We therefore insist that the following diagram commute:

This is called the wedge condition. It can be written as:

p ida f ∘ αa = p f idb ∘ αb

Or, using Haskell notation:

dimap id f . alpha = dimap f id . alpha

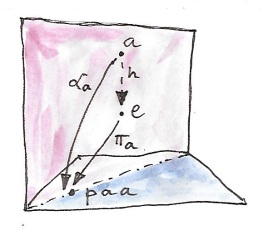
We can now proceed with the universal construction and define the end of p as the universal wedge — a set e together with a family of functions π such that for any other wedge with the apex a and a family α there is a unique function h::a->e that makes all triangles commute:

πa ∘ h = αa

The symbol for the end is the integral sign, with the “integration variable” in the subscript position:

∫c p c c

Components of π are called projection maps for the end:

πa :: ∫c p c c -> p a a

Note that if C is a discrete category (no morphisms other than the identities) the end is just a global product of all diagonal entries of p across the whole category C. Later I’ll show you that, in the more general case, there is a relationship between the end and this product through an equalizer.

In Haskell, the end formula translates directly to the universal quantifier:

forall a. p a a

Strictly speaking, this is just a product of all diagonal elements of p, but the wedge condition is satisfied automatically due to parametricity (I’ll explain it in a separate blog post). For any function f :: a -> b, the wedge condition reads:

dimap f id . pi = dimap id f . pi

or, with type annotations:

dimap f idb . pib = dimap ida f . pia

where both sides of the equation have the type:

Profunctor p => (forall c. p c c) -> p a b

and pi is the polymorphic projection:

pi :: Profunctor p => forall c. (forall a. p a a) -> p c c
pi e = e

Here, type inference automatically picks the right component of e.

Just as we were able to express the whole set of commutation conditions for a cone as one natural transformation, likewise we can group all the wedge conditions into one dinatural transformation. For that we need the generalization of the constant functor Δc to a constant profunctor that maps all pairs of objects to a single object c, and all pairs of morphisms to the identity morphism for this object. A wedge is a dinatural transformation from that functor to the profunctor p. Indeed, the dinaturality hexagon shrinks down to the wedge diamond when we realize that Δc lifts all morphisms to one identity function.

Ends can also be defined for target categories other than Set, but here we’ll only consider Set-valued profunctors and their ends.

Ends as Equalizers

The commutation condition in the definition of the end can be written using an equalizer. First, let’s define two functions (I’m using Haskell notation, because mathematical notation seems to be less user-friendly in this case). These functions correspond to the two converging branches of the wedge condition:

lambda :: Profunctor p => p a a -> (a -> b) -> p a b
lambda paa f = dimap id f paa

rho :: Profunctor p => p b b -> (a -> b) -> p a b
rho pbb f = dimap f id pbb

Both functions map diagonal elements of the profunctor p to polymorphic functions of the type:

type ProdP p = forall a b. (a -> b) -> p a b

Functions lambda and rho have different types. However, we can unify their types, if we form one big product type, gathering together all diagonal elements of p:

newtype DiaProd p = DiaProd (forall a. p a a)

The functions lambda and rho induce two mappings from this product type:

lambdaP :: Profunctor p => DiaProd p -> ProdP p
lambdaP (DiaProd paa) = lambda paa

rhoP :: Profunctor p => DiaProd p -> ProdP p
rhoP (DiaProd paa) = rho paa

The end of p is the equalizer of these two functions. Remember that the equalizer picks the largest subset on which two functions are equal. In this case it picks the subset of the product of all diagonal elements for which the wedge diagrams commute.

Natural Transformations as Ends

The most important example of an end is the set of natural transformations. A natural transformation between two functors F and G is a family of morphisms picked from hom-sets of the form C(F a, G a). If it weren’t for the naturality condition, the set of natural transformations would be just the product of all these hom-sets. In fact, in Haskell, it is:

forall a. f a -> g a

The reason it works in Haskell is because naturality follows from parametricity. Outside of Haskell, though, not all diagonal sections across such hom-sets will yield natural transformations. But notice that the mapping:

<a, b> -> C(F a, G b)

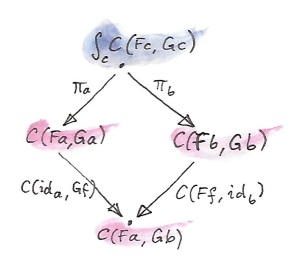
is a profunctor, so it makes sense to study its end. This is the wedge condition:

Let’s just pick one element from the set ∫c C(F c, G c). The two projections will map this element to two components of a particular transformation, let’s call them:

τa :: F a -> G a
τb :: F b -> G b

In the left branch, we lift a pair of morphisms <ida, G f> using the hom-functor. You may recall that such lifting is implemented as simultaneous pre- and post-composition. When acting on τa the lifted pair gives us:

G f ∘ τa ∘ ida

The other branch of the diagram gives us:

idb ∘ τb ∘ F f

Their equality, demanded by the wedge condition, is nothing but the naturality condition for τ.

Coends

As expected, the dual to an end is called a coend. It is constructed from a dual to a wedge called a cowedge (pronounced co-wedge, not cow-edge).

The symbol for a coend is the integral sign with the “integration variable” in the superscript position:

∫ c p c c

Just like the end is related to a product, the coend is related to a coproduct, or a sum (in this respect, it resembles an integral, which is a limit of a sum). Rather than having projections, we have injections going from the diagonal elements of the profunctor down to the coend. If it weren’t for the cowedge conditions, we could say that the coend of the profunctor p is either p a a, or p b b, or p c c, and so on. Or we could say that there exists such an a for which the coend is just the set p a a. The universal quantifier that we used in the definition of the end turns into an existential quantifier for the coend.

This is why, in pseudo-Haskell, we would define the coend as:

exists a. p a a

The standard way of encoding existential quantifiers in Haskell is to use universally quantified data constructors. We can thus define:

data Coend p = forall a. Coend (p a a)

The logic behind this is that it should be possible to construct a coend using a value of any of the family of types p a a, no matter what a we chose.

Just like an end can be defined using an equalizer, a coend can be described using a coequalizer. All the cowedge conditions can be summarized by taking one gigantic coproduct of p a b for all possible functions b->a. In Haskell, that would be expressed as an existential type:

data SumP p = forall a b. SumP (b -> a) (p a b)

There are two ways of evaluating this sum type, by lifting the function using dimap and applying it to the profunctor p:

lambda, rho :: Profunctor p => SumP p -> DiagSum p
lambda (SumP f pab) = DiagSum (dimap f id pab)
rho    (SumP f pab) = DiagSum (dimap id f pab)

where DiagSum is the sum of diagonal elements of p:

data DiagSum p = forall a. DiagSum (p a a)

The coequalizer of these two functions is the coend. A coequilizer is obtained from DiagSum p by identifying values that are obtained by applying lambda or rho to the same argument. Here, the argument is a pair consisting of a function b->a and an element of p a b. The application of lambda and rho produces two potentially different values of the type DiagSum p. In the coend, these two values are identified, making the cowedge condition automatically satisfied.

The process of identification of related elements in a set is formally known as taking a quotient. To define a quotient we need an equivalence relation ~, a relation that is reflexive, symmetric, and transitive:

a ~ a
if a ~ b then b ~ a
if a ~ b and b ~ c then a ~ c

Such a relation splits the set into equivalence classes. Each class consists of elements that are related to each other. We form a quotient set by picking one representative from each class. A classic example is the definition of rational numbers as pairs of whole numbers with the following equivalence relation:

(a, b) ~ (c, d) iff a * d = b * c

It’s easy to check that this is an equivalence relation. A pair (a, b) is interpreted as a fraction a/b, and fractions whose numerator and denominator have a common divisor are identified. A rational number is an equivalence class of such fractions.

You might recall from our earlier discussion of limits and colimits that the hom-functor is continuous, that is, it preserves limits. Dually, the contravariant hom-functor turns colimits into limits. These properties can be generalized to ends and coends, which are a generalization of limits and colimits, respectively. In particular, we get a very useful identity for converting coends to ends:

Set(∫ x p x x, c) ≅ ∫x Set(p x x, c)

Let’s have a look at it in pseudo-Haskell:

(exists x. p x x) -> c ≅ forall x. p x x -> c

It tells us that a function that takes an existential type is equivalent to a polymorphic function. This makes perfect sense, because such a function must be prepared to handle any one of the types that may be encoded in the existential type. It’s the same principle that tells us that a function that accepts a sum type must be implemented as a case statement, with a tuple of handlers, one for every type present in the sum. Here, the sum type is replaced by a coend, and a family of handlers becomes an end, or a polymorphic function.

Ninja Yoneda Lemma

The set of natural transformations that appears in the Yoneda lemma may be encoded using an end, resulting in the following formulation:

∫z Set(C(a, z), F z) ≅ F a

There is also a dual formula:

∫ z C(z, a) × F z ≅ F a

This identity is strongly reminiscent of the formula for the Dirac delta function (a function δ(a - z), or rather a distribution, that has an infinite peak at a = z). Here, the hom-functor plays the role of the delta function.

Together these two identities are sometimes called the Ninja Yoneda lemma.

To prove the second formula, we will use the consequence of the Yoneda embedding, which states that two objects are isomorphic if and only if their hom-functors are isomorphic. In other words a ≅ b if and only if there is a natural transformation of the type:

[C, Set](C(a, -), C(b, =))

that is an isomorphism.

We start by inserting the left-hand side of the identity we want to prove inside a hom-functor that’s going to some arbitrary object c:

Set(∫ z C(z, a) × F z, c)

Using the continuity argument, we can replace the coend with the end:

∫z Set(C(z, a) × F z, c)

We can now take advantage of the adjunction between the product and the exponential:

∫z Set(C(z, a), c(F z))

We can “perform the integration” by using the Yoneda lemma to get:

c(F a)

(Notice that we used the contravariant version of the Yoneda lemma, since c(F z) is contravariant in z.)
This exponential object is isomorphic to the hom-set:

Set(F a, c)

Finally, we take advantage of the Yoneda embedding to arrive at the isomorphism:

∫ z C(z, a) × F z ≅ F a

Profunctor Composition

Let’s explore further the idea that a profunctor describes a relation — more precisely, a proof-relevant relation, meaning that the set p a b represents the set of proofs that a is related to b. If we have two relations p and q we can try to compose them. We’ll say that a is related to b through the composition of q after p if there exist an intermediary object c such that both q b c and p c a are non-empty. The proofs of this new relation are all pairs of proofs of individual relations. Therefore, with the understanding that the existential quantifier corresponds to a coend, and the cartesian product of two sets corresponds to “pairs of proofs,” we can define composition of profunctors using the following formula:

(q ∘ p) a b = ∫ c p c a × q b c

Here’s the equivalent Haskell definition from Data.Profunctor.Composition, after some renaming:

data Procompose q p a b where
  Procompose :: q a c -> p c b -> Procompose q p a b

This is using generalized algebraic data type, or GADT syntax, in which a free type variable (here c) is automatically existentially quanitified. The (uncurried) data constructor Procompose is thus equivalent to:

exists c. (q a c, p c b)

The unit of so defined composition is the hom-functor — this immediately follows from the Ninja Yoneda lemma. It makes sense, therefore, to ask the question if there is a category in which profunctors serve as morphisms. The answer is positive, with the caveat that both associativity and identity laws for profunctor composition hold only up to natural isomorphism. Such a category, where laws are valid up to isomorphism, is called a bicategory (which is more general than a 2-category). So we have a bicategory Prof, in which objects are categories, morphisms are profunctors, and morphisms between morphisms (a.k.a., two-cells) are natural transformations. In fact, one can go even further, because beside profunctors, we also have regular functors as morphisms between categories. A category which has two types of morphisms is called a double category.

Profunctors play an important role in the Haskell lens library and in the arrow library.

Challenge

1. Write explicitly the cowedge condition for a coend.

Next: Kan extensions.

This is part 25 of Categories for Programmers. Previously: F-Algebras. See the Table of Contents.

If we interpret endofunctors as ways of defining expressions, algebras let us evaluate them and monads let us form and manipulate them. By combining algebras with monads we not only gain a lot of functionality but we can also answer a few interesting questions. One such question concerns the relation between monads and adjunctions. As we’ve seen, every adjunction defines a monad (and a comonad). The question is: Can every monad (comonad) be derived from an adjunction? The answer is positive. There is a whole family of adjunctions that generate a given monad. I’ll show you two such adjunction.

Let’s review the definitions. A monad is an endofunctor m equipped with two natural transformations that satisfy some coherence conditions. The components of these transformations at a are:

ηa :: a -> m a
μa :: m (m a) -> m a

An algebra for the same endofunctor is a selection of a particular object — the carrier a — together with the morphism:

alg :: m a -> a

The first thing to notice is that the algebra goes in the opposite direction to ηa. The intuition is that ηa creates a trivial expression from a value of type a. The first coherence condition that makes the algebra compatible with the monad ensures that evaluating this expression using the algebra whose carrier is a gives us back the original value:

alg ∘ ηa = ida

The second condition arises from the fact that there are two ways of evaluating the doubly nested expression m (m a). We can first apply μa to flatten the expression, and then use the evaluator of the algebra; or we can apply the lifted evaluator to evaluate the inner expressions, and then apply the evaluator to the result. We’d like the two strategies to be equivalent:

alg ∘ μa = alg ∘ m alg

Here, m alg is the morphism resulting from lifting alg using the functor m. The following commuting diagrams describe the two conditions (I replaced m with T in anticipation of what follows):

We can also express these condition in Haskell:

alg . return = id
alg . join = alg . fmap alg

Let’s look at a small example. An algebra for a list endofunctor consists of some type a and a function that produces an a from a list of a. We can express this function using foldr by choosing both the element type and the accumulator type to be equal to a:

foldr :: (a -> a -> a) -> a -> [a] -> a

This particular algebra is specified by a two-argument function, let’s call it f, and a value z. The list functor happens to also be a monad, with return turning a value into a singleton list. The composition of the algebra, here foldr f z, after return takes x to:

foldr f z [x] = x `f` z

where the action of f is written in the infix notation. The algebra is compatible with the monad if the following coherence condition is satisfied for every x:

x `f` z = x

If we look at f as a binary operator, this condition tells us that z is the right unit.

The second coherence condition operates on a list of lists. The action of join concatenates the individual lists. We can then fold the resulting list. On the other hand, we can first fold the individual lists, and then fold the resulting list. Again, if we interpret f as a binary operator, this condition tells us that this binary operation is associative. These conditions are certainly fulfilled when (a, f, z) is a monoid.

T-algebras

Since mathematicians prefer to call their monads T, they call algebras compatible with them T-algebras. T-algebras for a given monad T in a category C form a category called the Eilenberg-Moore category, often denoted by C^T. Morphisms in that category are homomorphisms of algebras. These are the same homomorphisms we’ve seen defined for F-algebras.

A T-algebra is a pair consisting of a carrier object and an evaluator, (a, f). There is an obvious forgetful functor UT from C^T to C, which maps (a, f) to a. It also maps a homomorphism of T-algebras to a corresponding morphism between carrier objects in C. You may remember from our discussion of adjunctions that the left adjoint to a forgetful functor is called a free functor.

The left adjoint to UT is called FT. It maps an object a in C to a free algebra in C^T. The carrier of this free algebra is T a. Its evaluator is a morphism from T (T a) back to T a. Since T is a monad, we can use the monadic μa (Haskell join) as the evaluator.

We still have to show that this is a T-algebra. For that, two coherence conditions must be satisified:

alg ∘ ηTa = idTa

alg ∘ μa = alg ∘ T alg

But these are just monadic laws, if you plug in μ for the algebra.

As you may recall, every adjunction defines a monad. It turns out that the adjunction between F^T and U^T defines the very monad T that was used in the construction of the Eilenberg-Moore category. Since we can perform this construction for every monad, we conclude that every monad can be generated from an adjunction. Later I’ll show you that there is another adjunction that generates the same monad.

Here’s the plan: First I’ll show you that FT is indeed the left adjoint of UT. I’ll do it by defining the unit and the counit of this adjunction and proving that the corresponding triangular identities are satisfied. Then I’ll show you that the monad generated by this adjunction is indeed our original monad.

The unit of the adjunction is the natural transformation:

η :: I -> UT ∘ FT

Let’s calculate the a component of this transformation. The identity functor gives us a. The free functor produces the free algebra (T a, μa), and the forgetful functor reduces it to T a. Altogether we get a mapping from a to T a. We’ll simply use the unit of the monad T as the unit of this adjunction.

Let’s look at the counit:

ε :: FT ∘ UT -> I

Let’s calculate its component at some T-algebra (a, f). The forgetful functor forgets the f, and the free functor produces the pair (T a, μa). So in order to define the component of the counit ε at (a, f), we need the right morphism in the Eilenberg-Moore category, or a homomorphism of T-algebras:

(T a, μa) -> (a, f)

Such homomorphism should map the carrier T a to a. Let’s just resurrect the forgotten evaluator f. This time we’ll use it as a homomorphism of T-algebras. Indeed, the same commuting diagram that makes f a T-algebra may be re-interpreted to show that it’s a homomorphism of T-algebras:

We have thus defined the component of the counit natural transformation ε at (a, f) (an object in the category of T-algebras) to be f.

To complete the adjunction we also need to show that the unit and the counit satisfy triangular identites. These are:

The first one holds because of the unit law for the monad T. The second is just the law of the T-algebra (a, f).

We have established that the two functors form an adjunction:

FT ⊣ UT

Every adjunction gives rise to a monad. The round trip

UT ∘ FT

is the endofunctor in C that gives rise to the corresponding monad. Let’s see what its action on an object a is. The free algebra created by FT is (T a, μa). The forgetful functor UT drops the evaluator. So, indeed, we have:

UT ∘ FT = T

As expected, the unit of the adjunction is the unit of the monad T.

You may remember that the counint of the adjunction produces monadic muliplication through the following formula:

μ = R ∘ ε ∘ L

This is a horizontal composition of three natural transformations, two of them being identity natural transformations mapping, respectively, L to L and R to R. The one in the middle, the counit, is a natural transformation whose component at an algebra (a, f) is f.

Let’s calculate the component μa. We first horizontally compose ε after FT, which results in the component of ε at FTa. Since FT takes a to the algebra (T a, μa), and ε picks the evaluator, we end up with μa. Horizontal composition on the left with UT doesn’t change anything, since the action of UT on morphisms is trivial. So, indeed, the μ obtained from the adjunction is the same as the μ of the original monad T.

The Kleisli Category

We’ve seen the Kleisli category before. It’s a category constructed from another category C and a monad T. We’ll call this category C_T. The objects in the Kleisli category C_T are the objects of C, but the morphisms are different. A morphism fK from a to b in the Kleisli category corresponds to a morphism f from a to T b in the original category. We call this morphism a Kleisli arrow from a to b.

Composition of morphisms in the Kleisli category is defined in terms of monadic composition of Kleisli arrows. For instance, let’s compose gK after fK. In the Kleisli category we have:

fK :: a -> b
gK :: b -> c

which, in the category C, corresponds to:

f :: a -> T b
g :: b -> T c

We define the composition:

hK = gK ∘ fK

as a Kleisli arrow in C

h :: a -> T c
h = μ ∘ (T g) ∘ f

In Haskell we would write it as:

h = join . fmap g . f

There is a functor F from C to C_T which acts trivially on objects. On morphims, it maps f in C to a morphism in C_T by creating a Kleisli arrow that embellishes the return value of f. Given a morphism:

f :: a -> b

it creates a morphism in C_T with the corresponding Kleisli arrow:

η ∘ f

In Haskell we’d write it as:

return . f

We can also define a functor G from C_T back to C. It takes an object a from the Kleisli category and maps it to an object T a in C. Its action on a morphism fK corresponding to a Kleisli arrow:

f :: a -> T b

is a morphism in C:

T a -> T b

given by first lifting f and then applying μ:

μb ∘ T f

In Haskell notation this would read:

G fT = join . fmap f

You may recognize this as the definition of monadic bind in terms of join.

It’s easy to see that the two functors form an adjunction:

F ⊣ G

and their composition G ∘ F reproduces the original monad T.

So this is the second adjunction that produces the same monad. In fact there is a whole category of adjunctions Adj(C, T) that result in the same monad T on C. The Kleisli adjunction we’ve just seen is the initial object in this category, and the Eilenberg-Moore adjunction is the terminal object.

Coalgebras for Comonads

Analogous constructions can be done for any comonad W. We can define a category of coalgebras that are compatible with a comonad. They make the following diagrams commute:

where coa is the coevaluation morphism of the coalgebra whose carrier is a:

coa :: a -> W a

and ε and δ are the two natural transformations defining the comonad (in Haskell, their components are called extract and duplicate).

There is an obvious forgetful functor UW from the category of these coalgebras to C. It just forgets the coevaluation. We’ll consider its right adjoint FW.

UW ⊣ FW

The right adjoint to a forgetful functor is called a cofree functor. FW generates cofree coalgebras. It assigns, to an object a in C, the coalgebra (W a, δa). The adjunction reproduces the original comonad as the composite UW ∘ FW.

Similarly, we can construct a co-Kleisli category with co-Kleisli arrows and regenerate the comonad from the corresponding adjunction.

Lenses

Let’s go back to our discussion of lenses. A lens can be written as a coalgebra:

coalgs :: a -> Store s a

for the functor Store s:

data Store s a = Store (s -> a) s

This coalgebra can be also expressed as a pair of functions:

set :: a -> s -> a
get :: a -> s

(Think of a as standing for “all,” and s as a “small” part of it.) In terms of this pair, we have:

coalgs a = Store (set a) (get a)

Here, a is a value of type a. Notice that partially applied set is a function s->a.

We also know that Store s is a comonad:

instance Comonad (Store s) where
  extract (Store f s) = f s
  duplicate (Store f s) = Store (Store f) s

The question is: Under what conditions is a lens a coalgebra for this comonad? The first coherence condition:

εa ∘ coalg = ida

translates to:

set a (get a) = a

This is the lens law that expresses the fact that if you set a field of the structure a to its previous value, nothing changes.

The second condition:

fmap coalg ∘ coalg = δa ∘ coalg

requires a little more work. First, recall the definition of fmap for the Store functor:

fmap g (Store f s) = Store (g . f) s

Applying fmap coalg to the result of coalg gives us:

Store (coalg . set a) (get a)

On the other hand, applying duplicate to the result of coalg produces:

Store (Store (set a)) (get a)

For these two expressions to be equal, the two functions under Store must be equal when acting on an arbitrary s:

coalg (set a s) = Store (set a) s

Expanding coalg, we get:

Store (set (set a s)) (get (set a s)) = Store (set a) s

This is equivalent to two remaining lens laws. The first one:

set (set a s) = set a

tells us that setting the value of a field twice is the same as setting it once. The second law:

get (set a s) = s

tells us that getting a value of a field that was set to s gives s back.

In other words, a well-behaved lens is indeed a comonad coalgebra for the Store functor.

Challenges

1. What is the action of the free functor F :: C -> CT on morphisms. Hint: use the naturality condition for monadic μ.
2. Define the adjunction:

   UW ⊣ FW

3. Prove that the above adjunction reproduces the original comonad.

Acknowledgment

I’d like to thank Gershom Bazerman for helpful comments.

Next: Ends and Coends.