The Monad is like a bellows:
it is empty yet infinitely capable.
The more you use it, the more it produces;
the more you talk about it, the less you understand.
–Monad Te Ching
I don’t know if I’m exaggerating but it seems like every programmer who gets monads posts a tutorial about them. (And each post begins with: There’s already a lot of monad tutorials on the Internet, but…) The reason is that getting monads it’s like a spiritual experience that you want to share with others.
When facing a monad, people often behave like the three blind men describing an elephant. You’ll see monads described as containers and monads described as actions. Some people see them as a cover-up for side effects, others as examples of endofunctors in Category Theory.
Monads are hard to describe because they don’t correspond to anything in our everyday experience. Compare this with Objects in Object-Oriented programming. Even an infant knows what an object is (something you can put in your mouth). What do you do with a monad?
But first, let me answer the pertinent question:
Why Bother?
Monads enable pure functional programmers to implement mutation, state, I/O, and a plethora of other things that are not functions. Well, you might say, they brought it on themselves. They tied their hands behind their backs and now they’re bragging that they can type with their toes. Why should we pay attention?
The thing is, all those non-functional things that we are so used to doing in imperative programming are also sources of a lot of troubles. Take side effects for instance. Smart programmers (read: the ones who burnt their fingers too many times) try to minimize the use of global and static variables for fear of side effects. That’s doable if you know what you’re doing. But the real game changer is multithreading. Controlling the sharing of state between threads is not just good programming practice– it’s a survival skill. Extreme programming models are in use that eliminate sharing altogether, like Erlang’s full isolation of processes and its restriction of message passing to values.
Monads stake the ground between total anarchy of imperative languages and the rigid dictatorship of Erlang-like isolationism. They don’t prohibit sharing or side effects but let you control them. And, since the control is exercised through the type system, a program that uses monads can be checked for correctness by the compiler. Considering how hard it it to test for data races in imperative programs, I think it’s worth investing some time to learn monads.
There is also a completely different motivation: metaprogramming. The template language used for metaprogramming in C++ is a pure functional language (see my blog post, What does Haskell have to do with C++?). If monads are so important in functional programming, they must also pop up in C++ metaprogramming. And indeed they do. I hope to discuss this topic in a future post.
So what’s a monad?
A Categorical Answer
If you don’t know anything about category theory, don’t get intimidated. This is really simple stuff and it will clarify a lot of things, not to mention earning you some bragging rights. My main goal is to share some intuitions from mathematics that will build foundations for a deeper understanding of monads in programming. In this installment I will explain categories, functors, and endofunctors, leading up to monads. I will give examples taken both from everyday life and from programming. I will really get into monads and their practical applications in the next installment, so be patient.
Categories
A category is a natural extension of our notion of sets and functions. The generalization of a set in a category is called an object (a pretty neutral term with little semantic ballast), and the generalization of a function is called a morphism. In fact, the standard example of a category is the category of sets and functions called (capital letter) Set.
A morphism (read “function”) goes from one object (read “set”) to another. Mathematical functions like sin or exp usually go from the set of real numbers to the set of real numbers. But you may also define functions like isPrime that go from natural numbers to Booleans, or a function price that goes from a set of goods to the set of numbers.
The only thing a mathematician needs to know about morphisms is that they can be composed. If you have a morphism from A to B, A->B, and another going from B to C, B->C, then they can be composed to a morphism from A to C, A->C. And just like the standard composition of functions, morphism composition must be associative, so we don’t need parentheses when composing more than two of them.
Actually, two things. There must be, for every object, a special morphism called identity that essentially does nothing and when composed with any other morphism reproduces the same morphism.
Just to throw you off the track, a category doesn’t have to be built on sets and functions. You can easily construct simple categories from blobs and arrows. Fig 1 shows such a category that contains two objects and four morphisms: arrows between them (formally, those arrows are ordered pairs of objects so, for instance, f is a pair (A, B)). You can easily check that any two morphisms can be composed and that the two moprphisms
iA and
iB serve as identities.
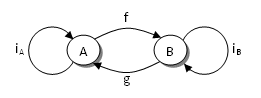
Fig 1. A simple category with two objects and four morphisms.
That’s it! Hopefully I have just convinced you that a category is not a big deal. But let’s get down to Earth. The one category that’s really important in programming languages is the category of types and functions, in particular its Haskell version called Hask. There usually is a finite set of basic types like integers or Booleans, and an infinite set of derived types, like lists of integers, functions from integers to Booleans, etc. In Hask, a type is just a set of values. For instance, the type Char is a set {‘a’, ‘b’, ‘c’, … }.
So, in the category Hask, types are objects and functions are morphisms. Indeed, a function maps one type into another (forget for a moment functions of multiple arguments– they can be modeled with currying– and polymorphic functions– they are families of functions). And these are functions in the functional-programming sense: called with the same values they return the same values–no side effects allowed.
Function composition is just passing the result of one function as an argument to another. The identity function takes x and immediately returns it back.
This is all fine, but what’s in it for me, you might ask. So here’s the first insight and a moment of Zen. If there is one thing that you can call the essence of programming, it’s composability. In any style of programming you always compose your program from smaller pieces, and those pieces from even smaller pieces, and so on. That’s why categories with their composable morphisms are so important. The essence of Lego blocks is the way they fit together, their composability, not the color or size. The essence of functional programming is how functions work together: how you can build larger functions from smaller ones.
Every category is defined by its choice of objects and morphisms. But is there something that can characterize a given category that’s independent of its choice of particular objects and morphisms? How do you expose the inner structure of a particular category? Mathematicians know exactly how to do that. You have to be able to map categories into other categories while preserving some constraints imposed by the way morphisms are attached to objects and the way they compose. Such maps let you find similarities between categories and catalog different kinds of categories. That’s when things get really interesting.
Functors
A functor, F, is a map from one category to another: it maps objects into objects and morphisms into morphisms. But it can’t do it in a haphazard way because that would destroy the very structures that we are after. So we must impose some “obvious” (mathematicians love that word) constraints.
First of all, if you have a morphism between two objects in the first category then it better be mapped into a morphism between the corresponding objects in the second category. Fig 2 explains this diagrammatically. Object A is mapped into F(A), object B into F(B). A morphism f from A to B is mapped into a morphism F(f) from F(A) to F(B). Mathematicians say that such a diagram must commute, that is the result must be the same whether you go from A to F(A) and then apply F(f), or first apply f and then go from B to F(B).
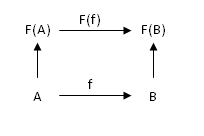
Fig 2. Diagram showing the action of a functor F on objects A and B and a morphism f. The bottom part lives in F's domain (source) category, the top part in its codomain (the target).
Moreover, such mapping should preserve the composition property of morphisms. So if morphism h is a composition of f and g, then F(h) must be a composition of F(f) and F(g). And, of course, the functor must map identity morphisms into identity morphisms.
To get a feel for how constrained functors are by these conditions, consider how you could map the category in Fig 1 into itself (such a functor just rearranges things inside one category). There are two trivial mappings that collapse both objects into one (either A or B), and turn all morphisms into identity. Then there is the identity functor that maps both objects into themselves and all morphisms into themselves. Finally, there is just one “interesting” functor that maps A into B and B into A with f and g switching roles. Now imagine a similar category but with the g arrow removed (yes, it’s still a category). Suddenly there is no functor other than the collapsing ones between Fig 1 and that new category. That’s because the two categories have completely different structure.
Let me now jump into more familiar territory. Since we are mostly interested in one category, Hask, let me define a functor that maps that category into itself (such functors are called endofunctors). An object in Hask is a type, so our functor must map types into types. The way to look at it is that a functor in Hask constructs one type from another– it’s a type constructor. Don’t get confused by the name: a type constructor creates a new type in your program, but that type has already existed in Hask.
A classical example is the list type constructor. Given any type it constructs a list of that type. Type Integer is mapped into list of integers or, in Haskell notation, [Integer]. Notice that this is not a map defined on integer values, like 1, 2, or 3. It also doesn’t add a new type to Hask— the type [Integer] is already there. It just maps one type into another. For C++ programmers: think of mapping type T into a container of T; for instance, std::vector<T>.
Mapping the types is the easy part, what about functions? We have to find a way to take a particular function and map it into a function on lists. That’s also easy: apply the function to each element of the list in turn. There is a (higher level) function in Haskel that does it. It’s called map and it takes a function and a list and returns a new list (or, because of currying, you may say that it takes a function and returns a function acting on lists). In C++ there is a corresponding template function called std::transform (well, it takes two iterators and a function object, but the idea is the same).
Mathematicians often use diagrams to illustrate the properties of morphisms and functors (see Fig 2). The arrows for morphisms are usually horizontal, while the arrows for functors are vertical (going up). That’s why the mapping of morphisms under a functor is often called lifting. You can take a function operating on integers and “lift it” (using a functor) to a function operating on lists of integers, and so on.
The list functor obviously preserves function composition and identity (I’ll leave it as an easy but instructive exercise for the reader).
And now for another moment of Zen. What’s the second most important property of programming? Reusability! Look what we have just done: We took all the functions we’ve implemented so far and lifted them to the level of lists. We’ve got functions operating on lists essentially for free (well, we’ve got a small but important subset of those functions). And the same trick may be applied to all kinds of containers, arrays, trees, queues, unique_ptrs and more.
It’s all beautiful, but you don’t really need category theory to apply functions to lists. Still it’s always good to see patterns in programming, and this one is definitely a keeper. The real revolution starts with monads. And, guess what, the list functor is actually a monad. You just need a few more ingredients.
What’s the intuition behind the statement that mappings expose the structure of the system? Consider the schematic of the London underground in Fig 3. It’s just a bunch of circles and lines. It’s only relevant because there is a mapping between the city of London and this schematic. The circles correspond to tube stations and the lines to train connections. Most importantly, if trains run between two stations, the corresponding circles in the diagram are connected by lines and vice versa: these are the constraints that the mapping preserves. The schematic shows a certain structure that exists in London (mostly hidden underground) which is made apparent by the mapping.

Fig 3. The schematic map of London underground system.
Interestingly, what I’m doing here is also mapping: London and the underground map correspond to two categories. Trains stations/circles are objects and train connections/lines are morphism. How’s that for an example?
Endofunctors
Mathematicians love mappings that preserve “obvious” constraints. As I explained, such mappings abstract inner structures away from the details of implementation. But you can also learn a lot about structure by studying non-trivial mappings into itself. Functors that map a category into itself are called endofunctors (like endo-scopes they let you look inside things). If functors expose similarities, endofunctors expose self-similarities. Take one look at the fractal fern, Fig 4, and you’ll understand how powerful self-similarity can be.

Fig 4. This fractal fern was generated using just four endomorphisms.
With a little bit of imagination you can see the list functor exposing fern-like structures inside Hask (Fig 5). Chars fan out into lists of Chars, which then fan out into lists of lists of Chars, and so on, ad infinitum. Horizontal structures described by functions from Char to Bool are reflected at higher and higher levels as functions on lists, lists of lists, etc.

Fig 5. The action of the list type constructor reveals fractal-like structure inside Hask. The functor lifts things up, the functions act horizontally.
A C++ template that takes a type parameter could be considered a type constructor. How likely is it that it also defines a functor (loosely speaking– C++ is not as mathematized as Haskell)? You have to ask yourself: Is the type parameter constrained in any way? It’s often hard to say, because type constraints are implicit in the body of a template and are tested only during instantiation. For instance, the type parameter for a std::vector must be copyable. That eliminates, for instance, classes that have private or deleted (in C++0x) copy constructors. This is not a problem though, because copyable types form a subcategory (I’m speaking really loosely now). The important thing is that a vector of copyable is itself copyable, so the “endo-” part of the endomorphism holds. In general you want to be able to feed the type created by the type constructor back to the type constructor, as in std::vector<std::vector<Foo>>. And, of course, you have to be able to lift functions in a generic way too, as in std::transform.
Monads
Ooh, Monads!
–Haskell Simpson
It’s time to finally lift the veil. I’ll start with the definition of a monad that builds on the previous sections and is mostly used by mathematicians. There is another one that’s less intuitive but easier to use in programming. I’ll leave that one for later.
A monad is an endofunctor together with two special families of morphisms, both going vertically, one up and one down (for “directions” see Fig 5). The one going up is called unit and the one going down is called join.
Now we are juggling a lot of mappings so let’s slow down to build some intuition. Remember, a functor maps objects: in our case, types, which are sets of values. The functor doesn’t see what’s inside the objects; morphisms, in general, do. In our case, a morphism is a function that maps values of one type into values of another type. Our functors, which are defined by type constructors, usually map poorer types into richer types; in the sense that type Bool is a set that contains just two elements, True and False, but type [Bool] contains infinitely many lists of True and False.
Unit takes a value from the poorer type, then picks one value from the richer type, and pronounces the two roughly equivalent. Such a rough equivalent of True from the Bool object is the one-element list [True] from the [Bool] object. Similarly, unit would map False into [False]. It would also map integer 5 into [5] and so on.
Unit can be thought of as immersing values from a lower level into the higher level in the most natural way possible. By the way, in programming we call a family of functions defined for any type a polymorphic function. In C++, we would express unit as a template, like this:
template<class T>
std::vector<T> unit(T value) {
std::vector<T> vec;
vec.push_back(value);
return vec;
}
To explain join, imagine the functor acting twice. For instance, from a given type T the list functor will first construct the type [T] (list of T), and then [[T]] (list of list of T). Join removes one layer of “listiness” by joining the sub-lists. Plainly speaking, it just concatenates the inner lists. Given, for instance, [[a, b], [c], [d, e]], it produces [a, b, c, d, e]. It’s a many-to-one mapping from the richer type to the poorer type and the type-parameterized family of joins also forms a polymorphic function (a template, in C++).
There are a few monadic axioms that define the properties of unit and join (for instance that unit and join cancel each other), but I’m not going to elaborate on them. The important part is that the existence of unit and join imposes new constraints on the endofunctor and thus exposes even more structure.
Mathematicians look at join as the grandfather of all multiplication with unit being its neutral element. It’s heaven for mathematicians because multiplication leads to algebraic structures and indeed monads are great for constructing algebras and finding their hidden properties.
Unlike mathematicians, we programmers are not that interested in algebraic structures. So there must be something else that makes monads such a hit. As I mentioned in the beginning, in programming we often face problems that don’t naturally translate into the functional paradigm. There are some types of computations that are best expressed in imperative style. It doesn’t mean they can’t be translated into functions, it’s just that the translation is somewhat awkward and tedious. Monads provide an elegant tool to do this translation. Monads made possible the absorption and assimilation of imperative programming into functional programming, so much so that some people claim (tongue in cheek?) that Haskell is the best imperative language. And like all things functional monads are bound to turn around and find their place in imperative programming. But that’s material for my next blog post.
Bibliography
Learning a new programming paradigm is like learning a foreign language. You learn the new vocabulary, the grammar, a few idioms, but you still formulate your thoughts in your native tongue. It takes years of immersion before you start thinking in a foreign language. In programming, the litmus test comes when you’re approaching a new problem. Will you formulate your solution in terms of the old or the new paradigm? Will you see procedures, objects, or functions?
I remember proposing an object oriented approach to the design of a content index back in my Microsoft years. The reaction was: It’s a great paradigm, but it’s not applicable to this particular problem. There are no “objects” in the content index. Indeed, you can’t find Employees and Payrolls, Students and Courses, DisplayableObjects and LightRays in the content index. But after a short brain storm we discovered such exotic objects as a Resource Manager or a Master Merge. We ended up with a fine piece of OO engineering that is still part of the Windows shell after all those years.
There’s a similar, if not larger, shift in thinking when you learn functional programming, especially if you come from an OO background. Initially you can’t help but see everything through the perspective of mutable data structures and loops. There are no obvious “functions” in your favorite problem. Functions are these weird stateless things–they always produce the same results when called with the same arguments. They are good in mathematics, but not in real-life programming.
And yet, there are people who write complete applications using functional (or at least hybrid) languages. One such example is the game The Path of Go created by Microsoft Research for the Xbox. It’s not a spectacular game as far as UI goes, but it plays some mean Go and it’s written in F#.
F# is a mostly functional language (based on ML) with support for object-oriented programming and access to the rich .NET libraries. In this respect it’s similar to Scala. Roughly: F# is to .NET what Scala is to JVM. Both languages were designed by excellent teams. F# was designed by Microsoft Research in Cambridge, England. The chief architect of F# is Don Syme. Scala is the brainchild of Martin Odersky.
I decided to learn F# and immerse myself in the new paradigm. So I had to pick a random problem, not one with obvious functional implementation, and start from scratch, design and all. In practice, I had to do a lot of experimenting in order to familiarize myself with the language and the library. Experimenting, by the way, was made relatively easy by the inclusion of an F# interpreter in Visual Studio 2010.
To learn F#, I used only online documentation which, as I found out, is not that good. There are also fewer online discussions about F# than, say, about Haskell. The two websites I used most are:
The Problem
Without further ado, let me describe the challenge:
Write a program that finds duplicate files on disk.
In particular, I was interested in finding duplicate image files, but for testing I used text files. The program should therefore concentrate on files with particular extensions. It should also be able to skip directories that I’m not interested in. The duplicates (or triplicates, etc.) don’t have to have the same names but have to have identical extensions and contents.
The Design
Not surprisingly, functional programming requires a major adjustment. It’s one thing to read somebody else’s code and admire the tricks, but a completely different thing to be designing and writing functional code from scratch. But once you get the hang of it, it actually becomes easy and quite natural.
The most important thing you notice when using functional languages is that types are mostly unobtrusive due to type inference, but type checking is very strong. Essentially, if you manage to compile your program, it usually runs correctly. You spend much less time debugging (which I found rather difficult in F#) and much more time figuring out why the types don’t match. Of course, you have to learn a whole new language of error messages.
So it’s definitely a steep learning curve but once you’re over the hump you start reaping the benefits.
The naive approach to solving my problem would be to list all files on disk (recursively, starting with the root directory) and compare each with each. That would scale very poorly, O(N2), so we need to do some pruning.
Let’s first group files by extension and size. There will be a lot of singleton groups– containing only one file with a particular combination of extension and size. Let’s eliminate them from consideration. After that we’ll be dealing with much smaller groups of files so, within those groups, we can do full-blown byte-by-byte comparisons. Strict comparisons will potentially split those groups into even smaller groups. Again, we should eliminate the resulting singletons. Finally, we should be able to print the resulting lists of lists of identical files.
For an imperative programmer the first impulse would be to use a lot of looping; e.g., for each file retrieve its extension and size, etc. An object-oriented programmer would use vectors, hash tables, and looping over iterators.
How would a functional programmer approach the subject? Iteration is out of the question. Recursion and immutable lists are in. Quite often functions operating on lists can be expressed as list comprehensions. But there’s an even better tool called sequences in F#. They’re sort of like iterators, but with some very nice compositional properties. Sequences can be composed using pipelining. So let me express the above design as a pipeline.
The Pipeline
This is the refinement of the original design that takes into account data structures: sequences, lists, and tuples in various combinations.
- The source for the pipeline is a sequence of file paths coming from a recursive enumerator.
- The first operation is to group the files that share the same key: in our case the key will be a tuple (file extension, file size).
- The next operation is to filter out groups of length one, the singletons.
- Since the grouping injected keys into our stream, we need to strip them now and convert groups to lists.
- Now we group byte-wise equal files within each group.
- Then we remove singletons within those subgroups,
- Flatten lists of lists, and
- Print the results.
There are only two stages that deal with technical details of data structures: the stripping of the keys and the flattening of the lists. Everything else follows from high-level design.
Here’s the pipeline in its full functional glory. The |> symbol is used to forward the results of one stage to the next.
enumFilesRec
(filterOutPaths ["c:\\Windows";"c:\\ProgramData";"c:\\Program Files"])
(filterExt [".jpg"; ".gif"])
"c:\\Multimedia"
|> Seq.groupBy (fun pth->(Path.GetExtension pth, (FileInfo pth).Length))
|> Seq.filter (fun (_, s) -> (Seq.length s) > 1)
|> Seq.map (fun (_, sq) -> [for path in sq -> path])
|> Seq.map groupEqualFiles
|> Seq.map filterOutSingletons
|> Seq.collect Seq.ofList
|> Seq.iter (fun lst -> printfn "%A" lst)
I will go through it line by line shortly.
I realize that this is a handful and if you have no previous experience with functional programming you are likely to feel overwhelmed at some point. The important thing is to observe how the original design translates almost one-to-one into implementation. Notice also the points of customization–they are almost universally plugs for user-defined functions. For instance, you customize Seq.map, Seq.filter, or Seq.collect by passing functions, often lambdas, as their arguments. Also, look how the function enumFilesRec is used. I decided to make its first two arguments functions even though my first impulse was to directly pass lists of directories to be skipped and extensions to be accepted. This way my design will work even if I later decide to filter files by, say, time of creation or size.
The Stages
Here’s the line by line reading of the pipeline code. My suggestion is to read as far as your patience permits and then skip to conclusions.
- I’m calling my function
enumFilesRec with three arguments:
enumFilesRec
(filterOutPaths ["c:\\Windows";"c:\\ProgramData";"c:\\Program Files"])
(filterExt [".jpg"; ".gif"])
"c:\\Multimedia"
- A directory filter: a function (predicate) that returns true for all directories except the ones listed as arguments to
filterOutPaths. It’s worth mentioning that filterOutPaths is a function that returns another function — the predicate expected by enumFilesRec.
- A file filter: a function that returns true only for listed extensions. Again,
filterExt is a function that takes a list and returns a predicate.
- The top directory: the root of the listing.
enumFilesRec returns a sequence of paths. Since the sequence is only evaluated on demand, the call to this function returns almost immediately.
- The next stage of the pipeline:
|> Seq.groupBy (fun p->(Path.GetExtension p, (FileInfo p).Length))
applies Seq.gropuBy to the incoming sequence of paths. Seq.groupBy takes one argument– a function that takes a path and generates a key:
fun path -> (Path.GetExtension path, (FileInfo path).Length)
The key is the tuple consisting of file extension and file length:
(Path.GetExtension path, (FileInfo path).Length)
F# notation for anonymous functions (lambdas) is of the form:
fun x -> expr
The function Seq.gropuBy groups all elements of the sequence into subgroups that share the same key. The result is a sequence of sequences (the groups). Of course, to perform this step the whole input sequence must be scanned. That forces the actual listing of directories on disk, which takes the bulk of the run time.
- The next stage performs
Seq.filter on the sequence:
|> Seq.filter (fun (_, s) -> (Seq.length s) > 1)
Seq.filter takes a predicate– here defined by a lambda– and applies it to all elements of the sequence; passing through only those that satisfy the predicate. This is the predicate:
fun (_, s) -> (Seq.length s) > 1
Notice that the previous step produced a sequence whose elements were tuples of (key, subsequence) with the subsequences sharing the same key. The lambda pattern-matches these tuples, (_, s), ignoring the key and testing the length of the subsequence against one. That eliminates singleton groups.
- We can now get rid of the keys and convert the subsequences into plain lists that will be needed for further processing.
|> Seq.map (fun (_, sq) -> [for path in sq -> path])
I use the workhorse of sequences, Seq.map, that applies a function to every element of the sequence. Remember that the element is still a tuple (key, subsequence). The lambda ignores the key and returns a list:
fun (_, sq) -> [for path in sq -> path]
The expression:
[for path in sq -> path]
enumerates the paths in the sequence sq and uses them to initialize a list (the brackets denote a list in F#). In functional programming such constructs are known as list comprehensions. The expression for path in sq -> path is called a generator.
- The next stage looks deceptively simple:
|> Seq.map groupEqualFiles
It applies a function, groupEqualsFiles to each list in the sequence. The interesting work happens in that function, which I will analyze shortly. Suffice it to say that it produces a list of sublists of identical files. Some of the sublists may be singletons.
It might be a little hard to keep track of all those sequences, subsequences, and sublists. A good development environment will show you all the types while you’re developing the program. You may also sketch simple examples:
seq[ [[a; a]; [b]]; [[c; c; c]; [d; d]; [e]] ]
This one shows a sequence of lists of lists of identical elements analogous to the output of the last stage.
- Next I apply another function,
filterOutSingletons to each list of sublists.
|> Seq.map filterOutSingletons
I end up with a sequence of lists of sublists of length greater than one containing identical files. The sequence above would be transformed to:
seq[ [[a; a]]; [[c; c; c]; [d; d]] ]
- In the next step I flatten this hierarchy using
Seq.collect.
|> Seq.collect Seq.ofList
Seq.collect takes a function that turns each element of the original sequence into a sequence and concatenates all those sequences into one. Like this:
seq[ [a; a]; [c; c; c]; [d; d] ]
Remember that the element of our sequence is a list of sublists. We can easily convert such a list to a sequence by applying Seq.ofList to it. It creates a sequence of sublists, and Seq.collect will concatenate all such sequences. I end up with a big sequence of lists. Those lists contain identical files. Voila!
- The final step is to print those lists.
|> Seq.iter (fun lst -> printfn "%A" lst)
I apply Seq.iter, which takes a void function (a function returning unit, in the F# parlance):
fun lst -> printfn "%A" lst
(which is really not a function because it has a side effect of printing its argument–a list). Seq.iter is just like Seq.map, but it consumes its input sequence producing nothing (except for side effects). Unlike Haskell, F# doesn’t track I/O side effects in the type system.
Details
For those who are really curious, I can go on filling in the details–the implementations of various functions used in the pipeline. Those functions use a variety of functional features of F# such as lists, recursion, pattern matching, etc. This is the bread and butter of functional programming.
Let me start with the function that enumerates files in a directory tree. The idea is to first list the files in the current directory and pass them through the file filter; then list the subdirectories, filter them through the directory filter, and recurse into each subdirectory. Since this function is the first stage of the pipeline, it should produce a sequence.
let rec enumFilesRec dirFilter fileFilter dir =
seq {
yield!
enumFilesSafe dir
|> Seq.filter fileFilter
yield!
enumDirsSafe dir
|> Seq.filter dirFilter
|> Seq.map (fun sub -> enumFilesRec dirFilter fileFilter sub)
|> Seq.collect id
}
Monads Anyone?
I don’t want to scare anyone but F# sequences are monads. People usually have strong feelings about monads, some love them, some hate them. But don’t get intimidated by monads. The theory behind them is hard, but the usage is pretty simple.
To create a sequence you use the seq { ... } block sprinkled with yield and yield! statements. When such a sequence is enumerated (you can do it with a loop for instance: for elem in sqnc), each yield returns an element and suspends the execution of the seq block until the next call. The next iteration resumes right after the last yield. In our case we are building a new sequence from existing ones. To dive into another sequence inside the seq block we use yield! (yield bang). This is what the above code does: It first dives into file enumeration (a sequence returned by enumFilesSafe) and then into the enumeration of files in subdirectories.
enumFilesSafe is a function that calls the system’s Directory.EnumerateFiles API (part of the .NET library). I had to encapsulate it into my own function in order to catch (and ignore) the UnauthorizedAccessExceptions. Notice the use of pipelining to filter the paths.
After the sequence of files paths is exhausted, we enter the second yield!. This one starts by enumerating subdirectories. Subdirectory paths are pipelined through the directory filter. Now we have to do something for each subdirectory– that’s the clue to use Seq.map. The mapping function:
fun sub -> enumFilesRec dirFilter fileFilter sub
simply calls enumFilesRec recursively, passing it the filters and the name of the subdirectory. Notice that enumFilseRec returns another sequence, so we end up with a sequence of sequences corresponding to individual subdirectories. To flatten this hierarchy I use Seq.collect. Notice that I pass it the identity function, id, which just returns its argument: The elements of my sequence are sequences and I don’t have to do anything to them.
The second function I’d like to discuss is groupEqualFiles. It gets a list of file paths and splits it into sublists containing byte-wise identical files. This problem can be decomposed in the following way: Let’s pick the first file and split the rest into two groups: the ones equal to that file and the ones not equal. Then do the same with the non-equal group. The “do the same” part hints at recursion. Here’s the code:
let groupEqualFiles paths =
let rec groupEqualFilesRec soFar lst =
match lst with
| [] -> soFar
| (file::tail) ->
let (eq, rest) = groupFilesEqualTo file tail
if rest.IsEmpty then eq::soFar
else groupEqualFilesRec (eq::soFar) rest
groupEqualFilesRec [] paths
A recursive solution often involves defining a recursive function and then calling it with some initial arguments. That’s the case here as well. The recursive function groupEqualFilesRec takes the accumulator, the soFar list, and a list of files to group.
let rec groupEqualFilesRec soFar lst =
match lst with
| [] -> soFar
| (file::tail) ->
let (eq, rest) = groupFilesEqualTo file tail
if rest.IsEmpty then eq::soFar
else groupEqualFilesRec (eq::soFar) rest
The new trick here is pattern matching. A list can be empty and match the pattern [], or it can be split into the head and tail using the pattern (file::tail). In the first case I return the soFar list and terminate recursion. Otherwise I call another function groupFilesEqualTo with the head and the tail of the list. This auxiliary function returns a tuple of lists: the equal group and the rest. Symbolically, when called with a and [b; a; c; b; d; a] it produces:
([a; a; a], [b; c; b; d])
The tuple is immediately pattern matched to (eq, rest) in:
let (eq, rest) = groupFilesEqualTo file tail
if the rest is empty, I prepend the eq list to the accumulator, soFar. Otherwise I recursively call groupEqualFilesRec with the augmented accumulator and the rest.
The function groupEqualFiles simply calls the recursive groupEqualFilesRec with an empty accumulator and the initial list. The result is a list of lists.
For completeness, here’s the implementation of the recursive function groupFilesEqualTo
let rec groupFilesEqualTo file files =
match files with
| [] -> ([file], [])
| (hd::tail) ->
let (eqs, rest) = (groupFilesEqualTo file tail)
if eqFiles file hd then (hd::eqs, rest) else (eqs, hd::rest)
Again, this function pattern-matches the list. If it’s empty, it returns a tuple consisting of the singleton list containing the file in question and the empty rest. Otherwise it calls itself recursively to group the tail. The result is pattern-matched into (eqs, rest). Now the comparison is made between the original file and the head of the original list (we could have done it before making the recursive call, but this way the code is more compact). If they match then the head is prepended to the list of equal files, otherwise it lands in the rest.
Did I mention there would be a test at the end? By now you should be able to analyze the implementation of filterOutSingletons:
let rec filterOutSingletons lstOfLst =
match lstOfLst with
| [] -> []
| (h::t) ->
let t1 = filterOutSingletons t
if (List.length h) > 1 then h::t1 else t1
Conclusions
I am not arguing that we should all switch to functional programming. For one thing, despite great progress, performance is still a problem in many areas. Immutable data structures are great, especially in concurrent programming, but can at times be awkward and inefficient. However, I strongly believe that any programmer worth his or her salt should be fluent with the functional paradigm.
The heart of programming is composition and reuse. In object-oriented programming you compose and reuse objects. In functional programming you do the same with functions. There are myriads of ways you can compose functions, the simplest being pipelining, passing functions as arguments, and returning functions from functions. There are lambdas, closures, continuations, comprehensions and, yes, monads. These are powerful tools in the hands of a skilled programmer. Not every problem fits neatly within the functional paradigm, but neither do all problems fit the OO paradigm. What’s important is having choices.
The code is available on GitHub.







