In the previous installment I introduced monads using two examples: the Maybe monad and the List monad. Admittedly, those weren’t the most exciting uses of monads, although they served the purpose of explaining the underlying theory. I also mentioned that monads were introduced into functional programming as a general solution for a variety of problems. One of those problems was representing stateful computations as functions.
Functions, State, and Side Effects
Here’s the problem: In functional languages, every time you call a function with the same arguments, it must return the same result. In fact, if the compiler detects such a situation, it is free to memoize the result of the first call and skip subsequent calls altogether. A stateful computation, on the other hand, might return different results every time it’s performed. It may, for instance, access some global or static variables. It may also modify those variables– in other words have side effects. In extreme cases a computation might be performed purely for side effects and not even bother to return any results.
This kind of behavior is often troublesome even in imperative programming. The use of global variables in particular is being discouraged. A better solution is to encapsulate the state and pass it explicitly to functions that use it. As a syntactic shortcut, in object-oriented languages, some of the state is regularly passed to functions (methods) as a hidden “this” or “self” argument. There’s even a syntax for composing such functions, as in this JavaScript snippet:
with(document) {
var t = title;
write(t + " and more");
}
Here, title is a property and write a method of the object document. (If you put on your monadic glasses, it almost looks like do notation.)
In functional languages we have one more limitation: we cannot mutate any data. There’s a standard way to overcome this limitation: Instead of modifying the data, you create a modified copy. This doesn’t even have to be expensive, if the language supports smart data structures that silently substitute references for copies whenever possible. Most operations on lists in Haskell are optimized this way, and there’s even a language, Clojure, at whose core are “persistent” data structures that behave as if they were immutable, but do a lot of sharing behind the scenes. Immutability is a very attractive feature when you are doing concurrent programming: access to immutable data requires no synchronization.
Taking all this into account, the way to translate stateful computations into functional language is to use functions that explicitly take state (encapsulated in some data structure) and return the, possibly modified, state together with the usual return value. For instance, a C++ “function”:
int pop() {
auto v = glob.top();
glob.pop();
return v;
}
that operates on a global vector, glob of the type std::vector<int>, would be turned into a Haskell function:
pop (ST lst) = (ST (tail lst), head lst)
operating on the state of type Stack:
newtype Stack = ST [Int]
The constructor ST creates a Stack from a list of integers. This constructor is also used for pattern matching, as in the argument of pop. The function head returns the first element of a list, tail returns the rest.
The signature of pop is characteristic of functions that operate on state:
top:: Stack-> (Stack, Int)
Such functions are often called “actions.”
There are two problems with this scheme: (1) It’s awkward, and (2) It doesn’t fit our monadic approach. In this example, the original computation (as expressed in C++) takes no arguments and returns an integer. Its functional counterpart takes a state and returns an integer combined with the state. It’s not clear how one would bind such functions together and use the convenient do notation.
We are on the right track though. We just need to get even more general: We need to separate the construction of an action from its execution. Our basic blocks will be functions that return actions– we’ll call them “monadic functions.” Since action is a function, we’ll be dealing with functions returning functions; or higher order functions.
Our goal is to find a way to compose monadic functions into larger monadic functions. A composite monadic function will return a composite action. We will then execute such action on a state, and get our result.
This new description fits the monadic pattern much better. We start with a generic stateful computation that takes an argument of type a and returns a value of type b, and we turn it into a (monadic) function that takes type a and returns an enriched type based on b. This time, though, the enriched type is a function type– an action. In general, an action is a function that takes a state (of some type S) and returns a tuple consisting of the (possibly modified) state and the value of type b.
S -> (S, b)
Here’s the first element of the monad– a type constructor: For any type t it defines a new type: an action to calculate a value of type t given a state. This type constructor is part of the state monad. Before we get to a more formal definition, let’s do some practice exercises.
The Monadic Calculator
There’s a perfect example of a stateful computation: a stack-based calculator. The state in this case is represented by the type Calc:
newtype Calc = Calc [Int]
that hides a list of integers– our calculator’s stack.
First, lets define a monadic function (a function that returns an action) that pops an element off the calculator’s stack. It will be a function returning a function, so we need to use lambdas.
popCalc =
\(Calc lst) -> (Calc (tail lst), head lst)
The body of the lambda is almost identical to the implementation of pop above. Notice that popCalc takes no arguments. Rather, the function that it produces takes a calculator as an argument and returns the calculator back, paired with the result–the value at the top of the stack. In other words, popCalc returns a promise to calculate the top of the calculator’s stack when the stack is available.
Here’s how you can use popCalc. First, you call it with no arguments and record the returned action. Next, you create a calculator (with a non-empty stack, otherwise the next line of code would bomb). You apply the action to that calculator and record the result– you pattern-match it to a tuple consisting of a changed calculator and a number. Finally you display that number. This is the actual output of a Haskell interpreter session:
> let f = popCalc
> let calc = Calc [3, 2, 1]
> let (calc', x) = f calc
> x
3
While we’re at it, we can similarly implement a pushCalc function:
pushCalc n =
\(Calc lst) -> (Calc (n:lst), ())
Notice that the lambda produced by pushCalc returns a modified calculator (argument n is prepended to the list) paired with a special value () of the type unit— a Haskell equivalent of void. The imperative equivalent of this function would return void and work only through side effects. Notice also that the lambda is actually a closure: it captures the outer variable n for later use.
Finally, we need a function that performs some calculation; after all we are implementing a calculator:
addCalc =
\(Calc lst) -> let (a:b:rest) = lst
in
(Calc ((a + b):rest), ())
Here I’m matching the calculator’s list with the pattern (a:b:rest) to retrieve the top two elements. The modified calculator has the sum of those two elements on the top of its stack.
We can use all these functions in combination to perform more complex operations, like adding two numbers. Here’s a piece code that might rival some of the Rube Goldberg creations:
add x y =
let pux = pushCalc x -- promise to push x
puy = pushCalc y -- promise to push y
axy = addCalc -- promise to add top numbers
pp = popCalc -- promise to pop the result
calc = Calc [] -- we need a calculator
(calc1, _) = pux calc -- actually push x
(calc2, _) = puy calc1 -- actually push y
(calc3, _) = axy calc2 -- actually add top numbers
(_, z) = pp calc3 -- actually pop the result
in
z -- return the result
But what we really want is to be able to combine smaller actions into larger actions. For that we have to define bind. The signature of bind, in this case, should be:
bind :: (Calc -> (Calc, a)) -> -- action
(a -> (Calc -> (Calc, b)) -> -- continuation
(Calc -> (Calc, b)) -- new action
I have highlighted our enriched types–the action types. This signature looks much more complex than the signature of the Maybe bind, but that’s only because the enriched type is itself a function type. Other than that, the structure is the same: bind accepts an action and a continuation and returns a new action. The continuation in this case takes an argument of type a (the value to be calculated by the first action) and returns the composite action.
In fact, if we define Action as a type alias:
type Action a = Calc -> (Calc, a)
the signature of bind can be abbreviated to:
bind :: (Action a) -> (a -> (Action b)) -> (Action b)
Now for the implementation. Since the result of bind is an action, it has to return a lambda of the appropriate signature.
bind act cont =
\calc -> ... produce (Calc, b) tuple ...
Bind is supposed to compose the action, act, with the continuation, cont. So it should first apply act to calc.
let (calc', v) = act calc
The result is a tuple (calc', v) with a new calculator and a value v of type a.
This is the v that the continuation expects, so the next step is to apply the continuation:
act' = cont v
The result of the continuation is a new action. This new action can then be executed, that is applied to the new calculator:
act' calc'
to produce the desired result– a tuple of the type (Calc, b).
Here’s the final code:
bind act cont =
\calc ->
let (calc', v) = act calc
act' = cont v
in
act' calc'
To complete our construction of the monad, we need to define return. The signature of return is:
return :: a -> Action a
and the implementation is pretty straightforward. It takes a value v and returns a promise to return this value.
return v = \calc -> (calc, v)
An astute reader might notice that nothing in this construction depends on the peculiarities of the type Calc. It will work for any type that is used to represent state. So we have in fact just constructed a generic state monad. The stack-based calculator is just a silly example of that monad.
It’s not difficult to implement bind as an infix operator, >>=, and turn the calculator into a monad that’s recognizable by the Haskell compiler (see Appendix 1). Then the relevant part of the add function may be rewritten in the do notation:
add x y = do
pushCalc x
pushCalc y
addCalc
r <- popCalc
return r
Let me present the same code without any syntactic sugar, using the cascading lambda-within-lambda notation:
add x y =
bind (pushCalc x)
(\() -> bind (pushCalc y)
(\() -> bind addCalc
(\() -> bind popCalc
(\z -> return z))))
This is not something you will see often in Haskell programs, but I will eventually want to go beyond Haskell. My goal is to connect back with C++, and this is the form that’s most convenient form making such a transition.
So let’s painstakingly analyze this code. We are binding the first action, (pushCalc x), to the rest of the code. The rest of the code is expressed as one huge lambda. To make these two parts fit together, their types have to match. The value produced by the action pushCalc is void (a.k.a., “unit”)– so it’s type is Action (). Therefore the lambda to which it binds must also take void, hence the notation:
\() -> ...
The body of that lambda is another bind, and so on, until we get to the interesting part, which is popCalc.
popCalc is an action that calculates a value: its signature is Action Int. This value is passed to the lambda to which popCalc is bound. Therefore this last lambda takes an Int argument, z. Finally, this value is enclosed in an action, and that’s done by the function return.
This unsugared notation elucidates one more aspect of the monadic approach that’s very relevant in the context of Haskell. Haskell is a lazy language: it doesn’t evaluate anything unless it is strictly necessary for achieving some final goal. Also, when it needs to evaluate several independent things, it will do that in some arbitrary, unpredictable order. So if it were somehow possible to implement the imperative versions of push and pop in Haskell, we would have two problems: push would never be evaluated because it produces no result, and even if it were, its evaluation could be swapped with the subsequent pop. Monadic bind forces the ordered evaluation of actions by introducing explicit data dependency. If pop follows push in the chain of binds, pop cannot be evaluated before push because its argument is the calculator that is returned by push. The two are linked by data dependency which, by the way, is not so obvious in the do notation.
Conclusion
The state monad is a very interesting pattern from the programming point of view. Instead of doing something, you create an action that is executed (maybe even multiple times) later. The monadic scaffolding provides the standard amenities like the ability to compose actions, and the do notation makes writing functions that produce functions much more natural. There is an interesting variation of the state monad called the IO monad, which is used for input and output in Haskell. I describe it in Appendix 2.
There are many patterns in imperative languages that have elements, or sometimes just hints, of a state monad. For instance, in the OO world you might encounter a very useful Command Pattern. You can “bind” command objects using the Composite Pattern. In languages that support anonymous functions and closures, like JavaScript, C# and, recently C++, you can return functions from functions directly. This might help, for instance, in dealing with inversion of control, where you return a closure as an event handler (that would be material for another series of blog posts).
But I have in mind a very specific example that I’ve been working on in C++ that fits the monadic pattern perfectly, and I’m going to write about it in the next installment of this series.
I’d like to thank Eric Niebler for valuable comments on the draft of this post.
Appendix 1
The full implementation of a stack-based calculator requires a few more Haskell tricks. First, we have to explicitly define our type constructor. I’ll call the new type Calculation, with the type constructor CL that encapsulates an action:
newtype Calculation a = CL (Calc -> (Calc, a))
Monadic functions have to return this new type, so they all wrap their actions into a Calculation.
pushCalc n =
CL (\(Calc lst) -> (Calc (n:lst), ()))
topCalc =
CL (\(Calc lst) -> (Calc lst, head lst))
popCalc =
CL (\(Calc lst) -> (Calc (tail lst), head lst))
addCalc =
CL (\(Calc lst) -> let (a:b:rest) = lst
in
(Calc ((a + b):rest), ()))
Haskell has a built-in type class for Monads (think of a type class as a C++ concept). We have to tell Haskell that our Calculation is an instance of Monad and provide the definition of the two associated functions: bind, using infix notation, and return.
instance Monad Calculation where
return x =
CL (\calc -> (calc, x))
CL(c) >>= cont =
CL (\calc ->
let (calc', v) = c calc
CL c' = cont v
in
c' calc')
With those definitions, our add function can be written using the do notation.
add x y = do
pushCalc x
pushCalc y
addCalc
r <- popCalc
return r
Since we are not expecting any values to be calculated by pushCalc or addCalc, there are no left arrows accompanying them in the do notation.
Appendix 1a: The Applicative
Haskell keeps evolving and, on occasion, the changes in the language break old code. In particular the Monad class has a superclass now, called Applicative. That’s why the Monad instance for Calculation won’t compile any more, unless you explicitly add the instance for Applicative. Fortunately, the Applicative functionality can be fully implemented using the Monad interface, as in:
instance Applicative Calculation where
pure = return
mf <*> mx = do f <- mf
x <- mx
return (f x)
This won’t compile either, because Applicative requires Functor as its superclass. So we have to make Applicative a Functor. The simplest is to let the compiler work it out, but you have to include this line at the very top of the file:
{-# LANGUAGE DeriveFunctor #-}
and modify the definition of Calculation:
newtype Calculation a = CL (Calc -> (Calc, a))
deriving Functor
In fact, it’s possible to implement the calculator as an Applicative, without the need for a Monad instance. But that’s a different story.
Appendix 2: The IO Monad
Strictly speaking a lazy purely functional language like Haskell cannot do any input or output. That’s because the compiler is free to memoize the result of the first call to, say, getChar and elide all subsequent calls. Calls to putChar, which don’t return anything, may be ignored altogether. This is why most functional languages cheat when it comes to I/O. But not Haskell. Monads to the rescue!
Let’s think for a moment why getChar may return different characters every time it’s called. It’s because there is a keyboard somewhere out there that changes its state. Why is it changing its state? Because there is a human who pushes the keys. Why is the human pushing the keys? Because he or she got a phone call from China that the price of rice is about to go up, so it makes sense to buy some futures. And so on… In other words there is this external world that is full of state.
What if we encapsulate that whole world in a hidden data structure and write our program as an action that operates on it? This is very similar to the state monad pattern except that here the programmer has no access to the state and cannot execute the action. The action is produced by main and passed to the system for execution. It’s the system, wink wink, that has access to “the world” and may pass it as a state argument to that action. Of course it’s all smoke and mirrors, but it successfully staves off the insanity of the external world from impinging on the purity of Haskell.
How does it work in practice? There is a monad called IO. It’s almost like a state monad, except that its type can’t be expressed in Haskell, because it would have to look something like this:
type IO a = World -> (World, a)
and we don’t know what World is. The main function in a Haskell program is a monadic IO action, usually:
main :: IO ()
with the type parameter a replaced by unit, (), (although any other type will work too).
The simplest main is just a single IO action:
main = putStrLn "Hello World!"
but in general main is a do block.
You might ask: If a Haskell program is one monadic IO action, then where does the traditional functional code go? The answer is that you can call traditional functions from anywhere in the do block. Even in my highly biased example there were several non-monadic function calls (head, tail, operator (+), etc.). Imagine a Haskell program as a tree: it’s trunk is monadic IO, and so are all the thick branches that have anything to do with I/O. But the thinner branches and leaves are your run of the mill functions that get (lazily) evaluated only when the main IO action is executed by the system.
Another interesting observation is that all functions that perform I/O have this information encoded in their type signature. Not in the type of its arguments, mind you, but in the return type. This is almost the opposite of what you see in imperative languages, where you’d have to pass some kind of I/O object (file or stream) to a procedure that performs I/O (except when that object is global, like standard input/output in C++). In Haskell, if you want your function to perform I/O, two things must happen: it must return an IO action that it internally constructs; and the action must find its way to the very top, to the main function. On the way up, it might be bound with other such actions either using bind or the do notation.
You might ask: How does Haskell make sure that all IO actions get to the top, so that the system may execute them? It doesn’t! But consider what you would have to do in order not to pass an action to the top. You’d have to explicitly ignore it, as in:
let _ = putStrLn "Don't print me!"
Ignoring things in Haskell is not a default thing.
In my previous post I talked about categories, functors, endofunctors, and a little about monads. Why didn’t I just start with a Haskell definition of a monad and skip the math? Because I believe that monads are bigger than that. I don’t want to pigeonhole monads based on some specific language or application. If you know what to look for you’ll find monads everywhere. Some languages support them better, as a single general abstraction, others require you to re-implement them from scratch for every use case. I want you to be able to look at a piece of C++ code and say, “Hey, that looks like a monad.” That’s why I started from category theory, which sits above all programming languages and provides a natural platform to talk about monads.
In this installment I will talk about some specific programming challenges that, on the surface, seem to have very little in common. I will show how they can be solved and how from these disparate solutions a pattern emerges that can be recognized as a monad. I’ll talk in some detail about the Maybe monad and the List monad, since they are simple and illustrate the basic ideas nicely. I will leave the really interesting examples, like the state monad and its variations, to the next installment.
Challenges of Functional Programming
You know what a function is: called with the same argument it always returns the same result. A lot of useful computations map directly to functions. Still, a lot don’t. We often have to deal with some notions of computations that are not functions. We can describe them in words or implement as procedures with side effects. In non-functional languages such computations are often called “functions” anyway– I’ll enclose such usage with quotation marks. Eugenio Moggi, the guy who introduced monads to computing, listed a few examples:
- Partial “functions”: For some arguments they never terminate (e.g., go into an infinite loop). These are not really functions in the mathematical sense.
- Nondeterministic “functions”: They don’t return a single result but a choice of results. Non-deterministic parsers are like this. When given an input, they return a set of possible parses. Which of them is right depends on the context. These are not really functions because a function must return a single value.
- “Functions” with side effects: They access and modify some external state and, when called repeatedly, return different results depending on that state.
- “Functions” that throw exceptions: They are not defined for certain arguments (or states) and they throw exceptions instead of returning a result.
- Continuations.
- Interactive input:
getchar is a good example. It’s result depends on what hits the keyboard.
- Interactive output:
putchar is a good example. It’s not a function because it doesn’t return anything (if it returns an error code, it doesn’t depend on the argument). Still, it can’t be just optimized away if we want any output to appear on the screen.
The amazing thing is that, using some creative thinking, all these problems can be solved using pure functional methods. I won’t discuss all of them, but I’ll show you a series of progressively more interesting examples.
Error Propagation and Exceptions
Who doesn’t deal with error propagation? Let’s dissect the problem: You are defining a computation that can return a valid result only for a subset of possible arguments. So what happens when the argument is “wrong”? Well, you can return an error.
In the simplest case you might add one extra bit, success or failure, to your result. Sometimes you can spare a bit in the result type: If the correct result is always a non-negative number, you may return negative one as an error. Or, if the result is a pointer, you might return a null pointer instead. But these are just small hacks introduced for the sake of performance. And, like most hacks, they can lead to dangerous code. Consider this (likely incorrect) code:
size_t off = fileName.find('.');
string ext = fileName.substr(off, fileName.length() - off);
If fileName contains no dot, the result is a special value npos signifying an error. The problem is that npos is of the same type as a non-error result, so it can be passed quietly to string::substr causing undefined behavior.
A more general and safer solution is to change– extend– the type of the result to include an error bit. You can do it for any type of result. In Haskell, you just define a type constructor called Maybe:
data Maybe a = Nothing | Just a
It takes an arbitrary type a and defines a new type that adds the special value Nothing to the set of possible values of a. In C++ that would be equivalent to a template:
template<class T>
struct Maybe {
T just; // valid if 'nothing' is false
bool nothing;
};
(This is just an example. I’m not arguing that Maybe would be very useful in C++ which has other mechanisms for error propagation.)
So here we have a way to turn a computation that’s not defined for all values into a function that’s defined over the whole domain, but which returns a new richer type.
The next question is, do these new things– functions returning Maybe— compose? What should the caller do with the result of such a function when it’s part of a larger computation? One thing is for sure, this result cannot be passed directly to an unsuspecting function–the error cannot be easily ignored– which is good. If we replace find by a new function safe_find that returns a Maybe<size_t>, the client won’t call substr with it. The types wouldn’t match. Instead, the result of safe_find must be unpacked and (much more likely than before) tested.
Maybe<size_t> off = safe_find(fileName, '.');
string ext;
if (!off.nothing)
ext = fileName.substr(off.just, fileName.length() - off.just);
Notice what happened here: By changing the return type of a function we broke the natural way functions compose– the result of one becoming the input of the next. On the other hand, we have come up with a new way of composing such functions. Let me chain a few of such compositions for better effect:
Maybe<Foo> foo = f(x);
if (!foo.nothing) {
Maybe<Bar> bar = g(foo.just);
if (!bar.nothing) {
Maybe<Baz> baz = h(bar.just);
if (!baz.nothing) {
...
}
}
}
I have highlighted the elements of the “glue,” which is used to compose our new, more error-conscious functions. Notice how this boilerplate glue gets in the way of code clarity. Ideally, we would like to write something like this:
DO
{
auto y = f(x);
auto v = g(y);
auto z = h(v);
return z;
}
where DO would magically provide the glue that’s implicit in the chaining of f, g, and h.
It’s not easy to do this– abstract the glue away– in C++. I’m not even going to try. But in Haskell it’s a different story. Let’s start with the almost direct translation of the C++ code into Haskell:
compose n =
let m = f n in
case m of
Nothing -> Nothing
Just n1 ->
let m1 = g n1 in
case m1 of
Nothing -> Nothing
Just n2 ->
let n3 = h n2 in
n3
The if statements are replaced by Haskell’s pattern matching (case x of). The ms are the Maybes and the ns art their contents (if they aren’t Nothings).
Notice the characteristic cascading style of this code– the nested conditionals or pattern matches. Let’s analyze one level of such a cascade. We start with a Maybe value (one returned by f n). We unpack it and examine the contents. If the result is not an error (Just n1), we continue with the rest of the body of compose. I have highlighted the “rest of the body” in blue (the “glue” is still in red).
What’s also important is that, if the result is an error (the Nothing branch of the pattern match) the whole “rest of the body” is skipped. In order to abstract the glue, we have to abstract the “rest of the body” as well. Such an abstraction is called a continuation. Let’s write this continuation as a lambda (lambdas in Haskell are written using the backslash, which is nothing but the Greek letter λ missing one leg):
\ n1 ->
let m1 = g n1 in
case m1 of
Nothing -> Nothing
Just n2 ->
let n3 = h n2 in
n3
And here’s the trick: We can abstract the glue as a (higher-order) function that takes a Maybe value and a continuation. Let’s call this new function bind and rewrite compose with its help:
compose n =
let m = f n in
-- the first argument is m, the second is the whole continuation
bind m (\n1 ->
let m1 = g n1 in
case m1 of
Nothing -> Nothing
Just n2 ->
let n3 = h n2 in
n3)
Here’s how bind is implemented:
bind m f =
case m of
Nothing -> Nothing -- bypass the continuation
Just n -> f n -- pass n to the continuation
or, more compactly,
bind Nothing cont = Nothing
bind (Just n) cont = cont n
Figure 1 illustrates the complete code transformation. The result of f n, which is a Maybe, is passed to bind, represented by a blue box. Inside bind the Maybe is unpacked. If its value is Nothing, nothing happens. If its value is Just n1, the rest of the code, the continuation, is called with the argument n1. The continuation itself is rewritten using bind, and so on. The final continuation calls return, which I will explain shortly.
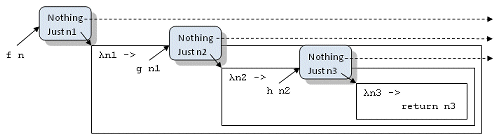
Fig 1. Composition of functions that return Maybe results
The position of bind, the blue box in Figure 1, between its Maybe argument and the continuation suggests that infix notation might be more appropriate. Indeed, in Haskell bind is represented by the infix operator, >>=:
Nothing >>= cont = Nothing
(Just x) >>= cont = cont x
(The left-hand side of the equal sign is the operator between its two arguments [actually, patterns], and the right-hand side is the body of the function.) We can express the type signature of the bind function as:
(>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b
It takes a Maybe a and a function from a to Maybe b (that’s our continuation). It returns a Maybe b. When dealing with higher order functions I find type signatures extremely useful; so much so that I often use them as comments in my C++ meta-code.
The complete rewrite of compose using >>= looks like this:
compose1 n =
f n >>= \n1 ->
g n1 >>= \n2 ->
h n2 >>= \n3 ->
return n3
Now is the time to explain the mysterious return at the end of the function. No, it’s not the keyword for returning a result from a function. It’s a function that takes an argument of type a and turns it into a Maybe a:
return n = Just n
We need return because the result of compose is a Maybe. If any of the functions returns Nothing, compose returns Nothing (it’s part of the definition of >>=). Only when all functions succeed do we call return with the correct result, n3. It turns n3 into Just n3, thus announcing the success of the computation and encapsulating the final result.
You might say that using return instead of Just n3 is an overkill, but there are good reasons to do that. One is to encapsulate and hide direct access to the implementation of Maybe. The other has to do with the ways this pattern is generalized beyond Maybe.
The Maybe Monad
What does Maybe have to do with monads? Let’s see what we have done so far from a more general perspective.
We started from a computation which didn’t behave like a function– here, it was not defined for all arguments. We had found a clever way to turn it into a function by enriching its return type. Such general “enriching” of types can be expressed as a type constructor.
From a category-theoretical point of view, defining a type constructor, which is a mapping from types to types, gets us half way towards defining an endofunctor. The other part is the mapping of functions (morphisms). For any function that takes values of type a and returns values of type b we need a corresponding function that acts between the enriched types. In Haskell, the mapping of functions to functions can be expressed as a higher-order function. When this mapping is part of an endofunctor, the corresponding higher-order function is called fmap.
Let’s call the type constructor M. It constructs the enriched type M a from any type a. The function fmap has the following signature:
fmap :: (a -> b) -> (M a -> M b)
It maps a function from a to b to a function from M a to M b. In the case of Maybe we already know the type constructor part, and fmap will follow soon.
Let’s go back to our computation turned function returning an enriched type. In general, its signature is:
f :: a -> M b
Since we care about composability of computations, we need a way to glue the enriched functions together. In the process of gluing we usually have to inspect the enriched type and make decisions based on its value. One of such decisions might be whether to continue with the rest of the computation or not. So the general bind operation must take two arguments: the result of the previous enriched function and the rest of the computation– a continuation:
bind :: M a -> (a -> M b) -> M b
If you squint enough, you can see a similarity between bind and fmap.
Here’s how you do it: Imagine that you supply bind with its second argument, the continuation. There is still one free parameter of the type M a. So what’s left is a function that takes M a and returns M b. (This is not exactly currying, since we are binding the second argument rather than the first, but the idea is the same.) That’s exactly the type of function that occurs on the right hand side of the signature of fmap. Seen from that point of view, bind maps functions into functions:
(a -> M b) -> (M a -> M b)
The function of the left hand side is our continuation, the one on the right hand side is bind with the second argument plugged by the continuation.
This signature is really close to that of fmap, but not quite. Luckily, we still have a second family of functions at our disposal, the polymorphic return. The signature of return is:
return :: a -> M a
Using both bind and return we can lift any function f:
f :: a -> b
to a function g:
g :: M a -> M b
Here’s the magic formula that defines g in terms of f, bind, and return (the dot denotes regular function composition):
g ma = bind ma (return . f)
Or, using infix notation:
g ma = ma >>= (return . f)
This mapping of f into g becomes our definition of fmap. Of course, fmap must obey some axioms, in particular it must preserve function composition and interact correctly with unit (which I will discuss shortly). These axioms translate back into corresponding conditions on bind and return, which I’m not going to discuss here.
Now that we have recovered the functor, we need the two other parts of a monad: unit and join. Guess what, return is just another name for unit. For any type, it lifts an element of that type to an element of the enriched type in the most natural manner (incidentally, the word natural has a very precise meaning in category theory; both unit and join are natural transformations of the functor (M, fmap)).
To recover join, let’s look at its type signature in Haskell:
join :: M (M a) -> M a
It collapses one layer of the type constructor. In the case of Maybe it should map a double Maybe to a single Maybe. It’s easy to figure out that it should map Just (Just x) into Just x and anything else to Nothing. But there is a more general way of defining join using bind combined with the identity function:
join :: M (M a) -> M a
join mmx = mmx >>= id
We are binding a value of type M (M a) to a function id. This function, when acting on M a returns M a. You can convince yourself that these signatures match the general signature of bind (see Appendix); and that this definition, when applied to Maybe, produces the correct result.
To summarize: What we have done here is to show that Maybe together with bind and return is a monad in the category-theory sense. Actually, we have shown something far more general: Any triple that consists of a type constructor and two functions bind and return that obey certain identities (axioms) define a monad. In category theory this triple is called a Kleisli triple and can be used as an alternative definition of a monad.
Syntactic Sugar
So far you’ve seen only the Maybe example, so it might seem like we are pulling out a monadic cannon to kill a mosquito. But, as you’ll see later, this same pattern pops up in a lot of places in various guises. In fact it’s so common in functional languages that it acquired its own syntactic sugar. In Haskell, this sugar is called the do notation. Let’s go back to the implementation of our function compose:
compose n =
f n >>= \n1 ->
g n1 >>= \n2 ->
h n2 >>= \n3 ->
return n3
Here’s exactly the same code in do notation:
compose n = do
n1 <- f n
n2 <- g n1
n3 <- h n2
return n3
This looks deceptively similar to an imperative program. In fact here’s a C++ version of it (for the sake of the argument let’s assume that f takes a pointer to Foo and h returns an integer) :
int compose(Foo * n)
{
auto n1 = f(n);
auto n2 = g(n1);
auto n3 = h(n2);
return n3;
}
Uh, one more thing. This is how you would call it:
try {
compose(pFoo);
}
catch(...) {
// error handling
}
In C++ you get virtually the same functionality not by modifying the return type, but by throwing an exception. (Now you may utter your first cry, “Hey, that looks like a monad!”, when looking at C++ code.)
Just like in our Haskell example, once any of the functions reports an error (throws an exception), the rest of the body of compose is skipped. You might say that C++ exceptions offer more power than the Maybe monad and you’ll be right. But that’s because I haven’t shown you the Error monad and the Exception monad.
Where Haskell’s Exception monad beats C++ exceptions is in type checking. Remember the unfortunate attempt at adding exceptions specification to the C++ type system? (Java went the same way.) Here’s what the C++ standard says:
An implementation shall not reject an expression merely because when executed it throws or might throw an exception that the containing function does not allow.
In other words, exceptions specifications are bona fide comments. Not so in Haskell! If a function returns a Maybe or Exception, that becomes part of its type signature which is checked both at the call site and at the function definition site. No cheating is allowed, period.
But the major difference between Haskell’s and C++’s approach is that the do notation generalizes to all monads, whereas C++ neat try/catch syntax applies only to exceptions.
A word of caution when reading Haskell monadic code. Despite similarities in usage, Haskell’s left arrow is not an assignment. The left hand side identifier corresponds to the argument of the continuation (which is the rest of the do block). It is the result of unpacking the outcome of the right hand side expression. This unpacking always happens inside bind.
Non-deterministic Computations
In the previous post I introduced the list monad by defining a functor and two families of functions. The type constructor part of the functor mapped any type a into the list of a, [a]. The part that acted on functions (now we know that, in general, it’s called fmap; but for lists it’s just map) worked by applying the function to each element of the list. The unit and the join were polymorphic functions. unit was defined as:
unit x = [x]
and join as concat.
Now I can tell you that the list monad provides the solution to the problem of implementing non-deterministic computations. Imagine parsing a non-deterministic grammar. A production might offer multiple alternative parse trees for the same input.
These types of computations may be simulated with functions returning lists of possible results. Here’s the same trick again: whatever type is returned by a deterministic parser (e.g., a parse-tree type), it’s now turned into an enriched type (a parse tree list).
We’ve already seen the category-theory construction of the list monad but here we are facing a slightly different problem: how to string together functions that return lists. We know that we have to define bind. It’s signature, in this case, would be:
bind :: [a] -> (a -> [b]) -> [b]
It takes a list (which is the result of a previous function) and a continuation, (a -> [b]), and must produce another list. The obvious thing is to apply the continuation to each element of the input list. But since the continuation also produces a list, we’ll end up with a list of lists. To get a single list as the result, we’ll simply concatenate the sublists. Here’s the final implementation:
xs >>= cont = concat (map cont xs)
The application of the continuation to each element of the input list is done using map.
Is this a coincidence that we were able to define bind in therms of join and fmap? Not at all. The general formula for converting the functor definition of a monad to a Kleisli triple is:
Now we know how to move between those two definitions back and forth.
Just as in the case of Maybe, we can apply the do notation to functions returning lists:
toss2Dice = do
n <- tossDie
m <- tossDie
return (n + m)
Here, tossDie returns the list of all possible outcomes of a die toss, and toss2Dice returns the list of all possible sums of the outcomes of a two-die toss.
An interesting observation is that the list monad is closely related to list comprehensions, down to the use of left arrows (in Haskell). For instance, the above example is equivalent to:
toss2Dice = [n + m | n <- tossDie, m <- tossDie]
Conclusions
There is a large class of computations that convert input to output in a non-functional way. Many of those can be expressed as functions that return “enriched” output. This enrichment of the output can be expressed in terms of a type constructor. This type constructor defines the first component of a monad.
Computations have to be composable, so we need a way of composing the enriched functions. This introduces the second component of the monad, the bind family of higher-order functions.
Finally, we should be able to construct functions that return enriched types, and for that we need the third component of the monad, the return family of functions. They convert regular values into their enriched counterparts.
I’ve shown you two examples of Haskell monads in action, but the real treat will come in the third installment of my mini-series. I’ll show you how to define and compose functions that, instead of returning regular values, return functions that calculate those values.
Appendix: Join From Bind
By popular demand (see comments), I decided to explain in more detail the typing of the formula:
join :: M (M a) -> M a
join mmx = mmx >>= id
At first look it seems like id doesn’t have the right signature for the second parameter to bind:
bind :: M a' -> (a' -> M b') -> M b'
(I changed the names of type arguments to a' and b' to avoid confusion.) However, notice that here we are calling bind with the first argument, mmx, of type M (M a). It means that a' in this particular instantiation of bind is (M a). The second argument to bind is id with the signature:
id: c -> c
Here, id will be called with c equal to (M a), so its return type will also be (M a). With those substitutions, bind will also return type (M a):
M (M a) -> (M a -> M a) -> M a
Thus the whole combination (mmx >>= id) ends up with the right type signature for join.
Bibliography
- Eugenio Moggi, Notions of Computation and Monads. This is a hard core research paper that started the whole monad movement in functional languages.
- Philip Wadler, Monads for Functional Programming. The classic paper introducing monads into Haskell.
- Tony Morris, What Does Monad Mean?
- Brian Beckman, Don’t fear the Monad
- Graham Hutton, Erik Meijer, Monadic Parsing in Haskell.
- Brian McNamara, Yannis Smaragdakis, Syntax sugar for FC++: lambda, infix, monads, and more. A C++ template library for functional programming that imitates Haskell pretty closely.

