Haskell

Archived Posts from this Category

April 5, 2022

Teaching optics through conspiracy theories

Posted by Bartosz Milewski under Category Theory, Functional Programming, Haskell, Lens, Programming
[5] Comments 

This post is based on the talk I gave at Functional Conf 2022. There is a video recording of this talk.

Disclaimers

Data types may contain secret information. Some of it can be extracted, some is hidden forever. We’re going to get to the bottom of this conspiracy.

No data types were harmed while extracting their secrets.

No coercion was used to make them talk.

We’re talking, of course, about unsafeCoerce, which should never be used.

Implementation hiding

The implementation of a function, even if it’s available for inspection by a programmer, is hidden from the program itself.

What is this function, with the suggestive name double, hiding inside?

x double x
2 4
3 6
-1 -2

Best guess: It’s hiding 2. It’s probably implemented as:

double x = 2 * x

How would we go about extracting this hidden value? We can just call it with the unit of multiplication:

double 1
> 2

Is it possible that it’s implemented differently (assuming that we’ve already checked it for all values of the argument)? Of course! Maybe it’s adding one, multiplying by two, and then subtracting two. But whatever the actual implementation is, it must be equivalent to multiplication by two. We say that the implementaion is isomorphic to multiplying by two.

Functors

Functor is a data type that hides things of type a. Being a functor means that it’s possible to modify its contents using a function. That is, if we’re given a function a->b and a functorful of a‘s, we can create a functorful of b‘s. In Haskell we define the Functor class as a type constructor equipped with the method fmap:

class Functor f where
  fmap :: (a -> b) -> f a -> f b

A standard example of a functor is a list of a‘s. The implementation of fmap applies a function g to all its elements:

instance Functor [] where
  fmap g [] = []
  fmap g (a : as) = (g a) : fmap g as

Saying that something is a functor doesn’t guarantee that it actually “contains” values of type a. But most data structures that are functors will have some means of getting at their contents. When they do, you can verify that they change their contents after applying fmap. But there are some sneaky functors.

For instance Maybe a tells us: Maybe I have an a, maybe I don’t. But if I have it, fmap will change it to a b.

instance Functor Maybe where
  fmap g Empty = Empty
  fmap g (Just a) = Just (g a)

A function that produces values of type a is also a functor. A function e->a tells us: I’ll produce a value of type a if you ask nicely (that is call me with a value of type e). Given a producer of a‘s, you can change it to a producer of b‘s by post-composing it with a function g :: a -> b:

instance Functor ((->) e) where
  fmap g f = g . f

Then there is the trickiest of them all, the IO functor. IO a tells us: Trust me, I have an a, but there’s no way I could tell you what it is. (Unless, that is, you peek at the screen or open the file to which the output is redirected.)

Continuations

A continuation is telling us: Don’t call us, we’ll call you. Instead of providing the value of type a directly, it asks you to give it a handler, a function that consumes an a and returns the result of the type of your choice:

type Cont a = forall r. (a -> r) -> r

You’d suspect that a continuation either hides a value of type a or has the means to produce it on demand. You can actually extract this value by calling the continuation with an identity function:

runCont :: Cont a -> a
runCont k = k id

In fact Cont a is for all intents and purposes equivalent to a–it’s isomorphic to it. Indeed, given a value of type a you can produce a continuation as a closure:

mkCont :: a -> Cont a
mkCont a = \k -> k a

The two functions, runCont and mkCont are the inverse of each other thus establishing the isomorphism Cont a ~ a.

The Yoneda Lemma

Here’s a variation on the theme of continuations. Just like a continuation, this function takes a handler of a‘s, but instead of producing an x, it produces a whole functorful of x‘s:

type Yo f a = forall x. (a -> x) -> f x

Just like a continuation was secretly hiding a value of the type a, this data type is hiding a whole functorful of a‘s. We can easily retrieve this functorful by using the identity function as the handler:

runYo :: Functor f => Yo f a -> f a
runYo g = g id

Conversely, given a functorful of a‘s we can reconstruct Yo f a by defining a closure that fmap‘s the handler over it:

mkYo :: Functor f => f a -> Yo f a
mkYo fa = \g -> fmap g fa

Again, the two functions, runYo and mkYo are the inverse of each other thus establishing a very important isomorphism called the Yoneda lemma:

Yo f a ~ f a

Both continuations and the Yoneda lemma are defined as polymorphic functions. The forall x in their definition means that they use the same formula for all types (this is called parametric polymorphism). A function that works for any type cannot make any assumptions about the properties of that type. All it can do is to look at how this type is packaged: Is it passed inside a list, a function, or something else. In other words, it can use the information about the form in which the polymorphic argument is passed.

Existential Types

One cannot speak of existential types without mentioning Jean-Paul Sartre.
sartre_22
An existential data type says: There exists a type, but I’m not telling you what it is. Actually, the type has been known at the time of construction, but then all its traces have been erased. This is only possible if the data constructor is itself polymorphic. It accepts any type and then immediately forgets what it was.

Here’s an extreme example: an existential black hole. Whatever falls into it (through the constructor BH) can never escape.

data BlackHole = forall a. BH a

Even a photon can’t escape a black hole:

bh :: BlackHole
bh = BH "Photon"

We are familiar with data types whose constructors can be undone–for instance using pattern matching. In type theory we define types by providing introduction and elimination rules. These rules tell us how to construct and how to deconstruct types.

But existential types erase the type of the argument that was passed to the (polymorphic) constructor so they cannot be deconstructed. However, not all is lost. In physics, we have Hawking radiation escaping a black hole. In programming, even if we can’t peek at the existential type, we can extract some information about the structure surrounding it.

Here’s an example: We know we have a list, but of what?

data SomeList = forall a. SomeL [a]

It turns out that to undo a polymorphic constructor we can use a polymorphic function. We have at our disposal functions that act on lists of arbitrary type, for instance length:

length :: forall a. [a] -> Int

The use of a polymorphic function to “undo” a polymorphic constructor doesn’t expose the existential type:

len :: SomeList -> Int
len (SomeL as) = length as

Indeed, this works:

someL :: SomeList
someL = SomeL [1..10]
> len someL
> 10

Extracting the tail of a list is also a polymorphic function. We can use it on SomeList without exposing the type a:

trim :: SomeList -> SomeList
trim (SomeL []) = SomeL []
trim (SomeL (a: as)) = SomeL as

Here, the tail of the (non-empty) list is immediately stashed inside SomeList, thus hiding the type a.

But this will not compile, because it would expose a:

bad :: SomeList -> a
bad (SomeL as) = head as

Producer/Consumer

Existential types are often defined using producer/consumer pairs. The producer is able to produce values of the hidden type, and the consumer can consume them. The role of the client of the existential type is to activate the producer (e.g., by providing some input) and passing the result (without looking at it) directly to the consumer.

Here’s a simple example. The producer is just a value of the hidden type a, and the consumer is a function consuming this type:

data Hide b = forall a. Hide a (a -> b)

All the client can do is to match the consumer with the producer:

unHide :: Hide b -> b
unHide (Hide a f) = f a

This is how you can use this existential type. Here, Int is the visible type, and Char is hidden:

secret :: Hide Int
secret = Hide 'a' (ord)

The function ord is the consumer that turns the character into its ASCII code:

> unHide secret
> 97

Co-Yoneda Lemma

There is a duality between polymorphic types and existential types. It’s rooted in the duality between universal quantifiers (for all, \forall) and existential quantifiers (there exists, \exists).

The Yoneda lemma is a statement about polymorphic functions. Its dual, the co-Yoneda lemma, is a statement about existential types. Consider the following type that combines the producer of x‘s (a functorful of x‘s) with the consumer (a function that transforms x‘s to a‘s):

data CoYo f a = forall x. CoYo (f x) (x -> a)

What does this data type secretly encode? The only thing the client of CoYo can do is to apply the consumer to the producer. Since the producer has the form of a functor, the application proceeds through fmap:

unCoYo :: Functor f => CoYo f a -> f a
unCoYo (CoYo fx g) = fmap g fx

The result is a functorful of a‘s. Conversely, given a functorful of a‘s, we can form a CoYo by matching it with the identity function:

mkCoYo :: Functor f => f a -> CoYo f a
mkCoYo fa = CoYo fa id

This pair of unCoYo and mkCoYo, one the inverse of the other, witness the isomorphism

CoYo f a ~ f a

In other words, CoYo f a is secretly hiding a functorful of a‘s.

Contravariant Consumers

The informal terms producer and consumer, can be given more rigorous meaning. A producer is a data type that behaves like a functor. A functor is equipped with fmap, which lets you turn a producer of a‘s to a producer of b‘s using a function a->b.

Conversely, to turn a consumer of a‘s to a consumer of b‘s you need a function that goes in the opposite direction, b->a. This idea is encoded in the definition of a contravariant functor:

class Contravariant f where
  contramap :: (b -> a) -> f a -> f b

There is also a contravariant version of the co-Yoneda lemma, which reverses the roles of a producer and a consumer:

data CoYo' f a = forall x. CoYo' (f x) (a -> x)

Here, f is a contravariant functor, so f x is a consumer of x‘s. It is matched with the producer of x‘s, a function a->x.

As before, we can establish an isomorphism

CoYo' f a ~ f a

by defining a pair of functions:

unCoYo' :: Contravariant f => CoYo' f a -> f a
unCoYo' (CoYo' fx g) = contramap g fx

mkCoYo' :: Contravariant f => f a -> CoYo' f a
mkCoYo' fa = CoYo' fa id

Existential Lens

A lens abstracts a device for focusing on a part of a larger data structure. In functional programming we deal with immutable data, so in order to modify something, we have to decompose the larger structure into the focus (the part we’re modifying) and the residue (the rest). We can then recreate a modified data structure by combining the new focus with the old residue. The important observation is that we don’t care what the exact type of the residue is. This description translates directly into the following definition:

data Lens' s a =
  forall c. Lens' (s -> (c, a)) ((c, a) -> s)

Here, s is the type of the larger data structure, a is the type of the focus, and the existentially hidden c is the type of the residue. A lens is constructed from a pair of functions, the first decomposing s and the second recomposing it.
SimpleLens

Given a lens, we can construct two functions that don’t expose the type of the residue. The first is called get. It extracts the focus:

toGet :: Lens' s a -> (s -> a)
toGet (Lens' frm to) = snd . frm

The second, called set replaces the focus with the new value:

toSet :: Lens' s a -> (s -> a -> s)
toSet (Lens' frm to) = \s a -> to (fst (frm s), a)

Notice that access to residue not possible. The following will not compile:

bad :: Lens' s a -> (s -> c)
bad (Lens' frm to) = fst . frm

But how do we know that a pair of a getter and a setter is exactly what’s hidden in the existential definition of a lens? To show this we have to use the co-Yoneda lemma. First, we have to identify the producer and the consumer of c in our existential definition. To do that, notice that a function returning a pair (c, a) is equivalent to a pair of functions, one returning c and another returning a. We can thus rewrite the definition of a lens as a triple of functions:

data Lens' s a = 
  forall c. Lens' (s -> c) (s -> a) ((c, a) -> s)

The first function is the producer of c‘s, so the rest will define a consumer. Recall the contravariant version of the co-Yoneda lemma:

data CoYo' f s = forall c. CoYo' (f c) (s -> c)

We can define the contravariant functor that is the consumer of c‘s and use it in our definition of a lens. This functor is parameterized by two additional types s and a:

data F s a c = F (s -> a) ((c, a) -> s)

This lets us rewrite the lens using the co-Yoneda representation, with f replaced by (partially applied) F s a:

type Lens' s a = CoYo' (F s a) s

We can now use the isomorphism CoYo' f s ~ f s. Plugging in the definition of F, we get:

Lens' s a ~ CoYo' (F s a) s
CoYo' (F s a) s ~ F s a s
F s a s ~ (s -> a) ((s, a) -> s)

We recognize the two functions as the getter and the setter. Thus the existential representation of the lens is indeed isomorphic to the getter/setter pair.

Type-Changing Lens

The simple lens we’ve seen so far lets us replace the focus with a new value of the same type. But in general the new focus could be of a different type. In that case the type of the whole thing will change as well. A type-changing lens thus has the same decomposition function, but a different recomposition function:

data Lens s t a b =
forall c. Lens (s -> (c, a)) ((c, b) -> t)

As before, this lens is isomorphic to a get/set pair, where get extracts an a:

toGet :: Lens s t a b -> (s -> a)
toGet (Lens frm to) = snd . frm

and set replaces the focus with a new value of type b to produce a t:

toSet :: Lens s t a b -> (s -> b -> t)
toSet (Lens frm to) = \s b -> to (fst (frm s), b)

Other Optics

The advantage of the existential representation of lenses is that it easily generalizes to other optics. The idea is that a lens decomposes a data structure into a pair of types (c, a); and a pair is a product type, symbolically c \times a

data Lens s t a b =
forall c. Lens (s -> (c, a))
               ((c, b) -> t)

A prism does the same for the sum data type. A sum c + a is written as Either c a in Haskell. We have:

data Prism s t a b =
forall c. Prism (s -> Either c a)
                (Either c b -> t)

We can also combine sum and product in what is called an affine type c_1 + c_2 \times a. The resulting optic has two possible residues, c1 and c2:

data Affine s t a b =
forall c1 c2. Affine (s -> Either c1 (c2, a))
                     (Either c1 (c2, b) -> t)

The list of optics goes on and on.

Profunctors

A producer can be combined with a consumer in a single data structure called a profunctor. A profunctor is parameterized by two types; that is p a b is a consumer of a‘s and a producer of b‘s. We can turn a consumer of a‘s and a producer of b‘s to a consumer of s‘s and a producer of t‘s using a pair of functions, the first of which goes in the opposite direction:

class Profunctor p where
  dimap :: (s -> a) -> (b -> t) -> p a b -> p s t

The standard example of a profunctor is the function type p a b = a -> b. Indeed, we can define dimap for it by precomposing it with one function and postcomposing it with another:

instance Profunctor (->) where
  dimap in out pab = out . pab . in

Profunctor Optics

We’ve seen functions that were polymorphic in types. But polymorphism is not restricted to types. Here’s a definition of a function that is polymorphic in profunctors:

type Iso s t a b = forall p. Profunctor p =>
  p a b -> p s t

This function says: Give me any producer of b‘s that consumes a‘s and I’ll turn it into a producer of t‘s that consumes s‘s. Since it doesn’t know anything else about its argument, the only thing this function can do is to apply dimap to it. But dimap requires a pair of functions, so this profunctor-polymorphic function must be hiding such a pair:

s -> a
b -> t

Indeed, given such a pair, we can reconstruct it’s implementation:

mkIso :: (s -> a) -> (b -> t) -> Iso s t a b
mkIso g h = \p -> dimap g h p

All other optics have their corresponding implementation as profunctor-polymorphic functions. The main advantage of these representations is that they can be composed using simple function composition.

Main Takeaways

  • Producers and consumers correspond to covariant and contravariant functors
  • Existential types are dual to polymorphic types
  • Existential optics combine producers with consumers in one package
  • In such optics, producers decompose, and consumers recompose data
  • Functions can be polymorphic with respect to types, functors, or profunctors
 

June 15, 2020

Monoidal Catamorphisms

Posted by Bartosz Milewski under Category Theory, Haskell
[4] Comments 

I have recently watched a talk by Gabriel Gonzalez about folds, which caught my attention because of my interest in both recursion schemes and optics. A Fold is an interesting abstraction. It encapsulates the idea of focusing on a monoidal contents of some data structure. Let me explain.

Suppose you have a data structure that contains, among other things, a bunch of values from some monoid. You might want to summarize the data by traversing the structure and accumulating the monoidal values in an accumulator. You may, for instance, concatenate strings, or add integers. Because we are dealing with a monoid, which is associative, we could even parallelize the accumulation.

In practice, however, data structures are rarely filled with monoidal values or, if they are, it’s not clear which monoid to use (e.g., in case of numbers, additive or multiplicative?). Usually monoidal values have to be extracted from the container. We need a way to convert the contents of the container to monoidal values, perform the accumulation, and then convert the result to some output type. This could be done, for instance by fist applying fmap, and then traversing the result to accumulate monoidal values. For performance reasons, we might prefer the two actions to be done in a single pass.

Here’s a data structure that combines two functions, one converting a to some monoidal value m and the other converting the final result to b. The traversal itself should not depend on what monoid is being used so, in Haskell, we use an existential type.

data Fold a b = forall m. Monoid m => Fold (a -> m) (m -> b)

The data constructor of Fold is polymorphic in m, so it can be instantiated for any monoid, but the client of Fold will have no idea what that monoid was. (In actual implementation, the client is secretly passed a table of functions: one to retrieve the unit of the monoid, and another to perform the mappend.)

The simplest container to traverse is a list and, indeed, we can use a Fold to fold a list. Here’s the less efficient, but easy to understand implementation

fold :: Fold a b -> [a] -> b
fold (Fold s g) = g . mconcat . fmap s

See Gabriel’s blog post for a more efficient implementation.

A Fold is a functor

instance Functor (Fold a) where
  fmap f (Fold scatter gather) = Fold scatter (f . gather)

In fact it’s a Monoidal functor (in category theory, it’s called a lax monoidal functor)

class Monoidal f where
  init :: f ()
  combine :: f a -> f b -> f (a, b)

You can visualize a monoidal functor as a container with two additional properties: you can initialize it with a unit, and you can coalesce a pair of containers into a container of pairs.

instance Monoidal (Fold a) where
  -- Fold a ()
  init = Fold bang id
  -- Fold a b -> Fold a c -> Fold a (b, c)
  combine (Fold s g) (Fold s' g') = Fold (tuple s s') (bimap g g')

where we used the following helper functions

bang :: a -> ()
bang _ = ()

tuple :: (c -> a) -> (c -> b) -> (c -> (a, b))
tuple f g = \c -> (f c, g c)

This property can be used to easily aggregate Folds.

In Haskell, a monoidal functor is equivalent to the more common applicative functor.

A list is the simplest example of a recursive data structure. The immediate question is, can we use Fold with other recursive data structures? The generalization of folding for recursively-defined data structures is called a catamorphism. What we need is a monoidal catamorphism.

Algebras and catamorphisms

Here’s a very short recap of simple recursion schemes (for more, see my blog). An algebra for a functor f with the carrier a is defined as

type Algebra f a = f a -> a


Think of the functor f as defining a node in a recursive data structure (often, this functor is defined as a sum type, so we have more than one type of node). An algebra extracts the contents of this node and summarizes it. The type a is called the carrier of the algebra.

A fixed point of a functor is the carrier of its initial algebra

newtype Fix f = Fix { unFix :: f (Fix f) }


Think of it as a node that contains other nodes, which contain nodes, and so on, recursively.

A catamorphism generalizes a fold

cata :: Functor f => Algebra f a -> Fix f -> a
cata alg = alg . fmap (cata alg) . unFix

It’s a recursively defined function. It’s first applied using fmap to all the children of the node. Then the node is evaluated using the algebra.

Monoidal algebras

We would like to use a Fold to fold an arbitrary recursive data structure. We are interested in data structures that store values of type a which can be converted to monoidal values. Such structures are generated by functors of two arguments (bifunctors).

class Bifunctor f where
  bimap :: (a -> a') -> (b -> b') -> f a b -> f a' b'


In our case, the first argument will be the payload and the second, the placeholder for recursion and the carrier for the algebra.

We start by defining a monoidal algebra for such a functor by assuming that it has a monoidal payload, and that the child nodes have already been evaluated to a monoidal value

type MAlgebra f = forall m. Monoid m => f m m -> m

A monoidal algebra is polymorphic in the monoid m reflecting the requirement that the evaluation should only be allowed to use monoidal unit and monoidal multiplication.

A bifunctor is automatically a functor in its second argument

instance Bifunctor f => Functor (f a) where
  fmap g = bimap id g

We can apply the fixed point to this functor to define a recursive data structure Fix (f a).

We can then use Fold to convert the payload of this data structure to monoidal values, and then apply a catamorphism to fold it

cat :: Bifunctor f => MAlgebra f -> Fold a b -> Fix (f a) -> b
cat malg (Fold s g) = g . cata alg
  where
    alg = malg . bimap s id

Here’s this process in more detail. This is the monoidal catamorphism that we are defining:

We first apply cat, recursively, to all the children. This replaces the children with monoidal values. We also convert the payload of the node to the same monoid using the first component of Fold. We can then use the monoidal algebra to combine the payload with the results of folding the children.

Finally, we convert the result to the target type.

We have factorized the original problem in three orthogonal directions: the monoidal algebra, the Fold, and the traversal of the particular recursive data structure.

Example

Here’s a simple example. We define a bifunctor that generates a binary tree with arbitrary payload a stored at the leaves

data TreeF a r = Leaf a | Node r r

It is indeed a bifunctor

instance Bifunctor TreeF where
  bimap f g (Leaf a) = Leaf (f a)
  bimap f g (Node r r') = Node (g r) (g r')

The recursive tree is generated as its fixed point

type Tree a = Fix (TreeF a)

Here’s an example of a tree

We define two smart constructors to simplify the construction of trees

leaf :: a -> Tree a
leaf a = Fix (Leaf a)

node :: Tree a -> Tree a -> Tree a
node t t' = Fix (Node t t')

We can define a monoidal algebra for this functor. Notice that it only uses monoidal operations (we don’t even need the monoidal unit here, since values are stored in the leaves). It will therefore work for any monoid

myAlg :: MAlgebra TreeF
myAlg (Leaf m) = m
myAlg (Node m m') = m <> m'

Separately, we define a Fold whose internal monoid is Sum Int. It converts Double values to this monoid using floor, and converts the result to a String using show

myFold :: Fold Double String
myFold = Fold floor' show'
  where
    floor' :: Double -> Sum Int
    floor' = Sum . floor
    show' :: Sum Int -> String
    show' = show . getSum

This Fold has no knowledge of the data structure we’ll be traversing. It’s only interested in its payload.

Here’s a small tree containing three Doubles

myTree :: Tree Double
myTree = node (node (leaf 2.3) (leaf 10.3)) (leaf 1.1)

We can monoidally fold this tree and display the resulting String

Notice that we can use the same monoidal catamorphism with any monoidal algebra and any Fold.

The following pragmas were used in this program

{-# language ExistentialQuantification #-}
{-# language RankNTypes #-}
{-# language FlexibleInstances #-}
{-# language IncoherentInstances #-}

Relation to Optics

A Fold can be seen as a form of optic. It takes a source type, extracts a monoidal value from it, and maps a monoidal value to the target type; all the while keeping the monoid existential. Existential types are represented in category theory as coends—here we are dealing with a coend over the category of monoids \mathbf{Mon}(\mathbf{C}) in some monoidal category \mathbf C. There is an obvious forgetful functor U that forgets the monoidal structure and produces an object of \mathbf C. Here’s the categorical formula that corresponds to Fold

\int^{m \in Mon(C)} C(s, U m)\times C(U m, t)

This coend is taken over a profunctor in the category of monoids

P n m = C(s, U m) \times C(U n, t)

The coend is defined as a disjoint union of sets P m m in which we identify some of the elements. Given a monoid homomorphism f \colon m \to n, and a pair of morphisms

u \colon s \to U m

v \colon U n \to t

we identify the pairs

((U f) \circ u, v) \sim (u, v \circ (U f))

This is exactly what we need to make our monoidal catamorphism work. This condition ensures that the following two scenarios are equivalent:

  • Use the function u to extract monoidal values, transform these values to another monoid using f, do the folding in the second monoid, and translate the result using v
  • Use the function u to extract monoidal values, do the folding in the first monoid, use f to transform the result to the second monoid, and translate the result using v

Since the monoidal catamorphism only uses monoidal operations and f is a monoid homomorphism, this condition is automatically satisfied.

 

March 27, 2019

Promonads, Arrows, and Einstein Notation for Profunctors

Posted by Bartosz Milewski under Category Theory, Haskell, Monads, Programming
1 Comment 

I’ve been working with profunctors lately. They are interesting beasts, both in category theory and in programming. In Haskell, they form the basis of profunctor optics–in particular the lens library.

Profunctor Recap

The categorical definition of a profunctor doesn’t even begin to describe its richness. You might say that it’s just a functor from a product category \mathbb{C}^{op}\times \mathbb{D} to Set (I’ll stick to Set for simplicity, but there are generalizations to other categories as well).

A profunctor P (a.k.a., a distributor, or bimodule) maps a pair of objects, c from \mathbb{C} and d from \mathbb{D}, to a set P(c, d). Being a functor, it also maps any pair of morphisms in \mathbb{C}^{op}\times \mathbb{D}:

f\colon c' \to c
g\colon d \to d'

to a function between those sets:

P(f, g) \colon P(c, d) \to P(c', d')

Notice that the first morphism f goes in the opposite direction to what we normally expect for functors. We say that the profunctor is contravariant in its first argument and covariant in the second.

But what’s so special about this particular combination of source and target categories?

Hom-Profunctor

The key point is to realize that a profunctor generalizes the idea of a hom-functor. Like a profunctor, a hom-functor maps pairs of objects to sets. Indeed, for any two objects in \mathbb{C} we have the set of morphisms between them, C(a, b).

Also, any pair of morphisms in \mathbb{C}:

f\colon a' \to a
g\colon b \to b'

can be lifted to a function, which we will denote by C(f, g), between hom-sets:

C(f, g) \colon C(a, b) \to C(a', b')

Indeed, for any h \in C(a, b) we have:

C(f, g) h = g \circ h \circ f \in C(a', b')

This (plus functorial laws) completes the definition of a functor from \mathbb{C}^{op}\times \mathbb{C} to Set. So a hom-functor is a special case of an endo-profunctor (where \mathbb{D} is the same as \mathbb{C}). It’s contravariant in the first argument and covariant in the second.

For Haskell programmers, here’s the definition of a profunctor from Edward Kmett’s Data.Profunctor library:

class Profunctor p where
  dimap :: (a' -> a) -> (b -> b') -> p a b -> p a' b'

The function dimap does the lifting of a pair of morphisms.

Here’s the proof that the hom-functor which, in Haskell, is represented by the arrow ->, is a profunctor:

instance Profunctor (->) where
  dimap ab cd bc = cd . bc . ab

Not only that: a general profunctor can be considered an extension of a hom-functor that forms a bridge between two categories. Consider a profunctor P spanning two categories \mathbb{C} and \mathbb{D}:

P \colon \mathbb{C}^{op}\times \mathbb{D} \to Set

For any two objects from one of the categories we have a regular hom-set. But if we take one object c from \mathbb{C} and another object d from \mathbb{D}, we can generate a set P(c, d). This set works just like a hom-set. Its elements are called heteromorphisms, because they can be thought of as representing morphism between two different categories. What makes them similar to morphisms is that they can be composed with regular morphisms. Suppose you have a morphism in \mathbb{C}:

f\colon c' \to c

and a heteromorphism h \in P(c, d). Their composition is another heteromorphism obtained by lifting the pair (f, id_d). Indeed:

P(f, id_d) \colon P(c, d) \to P(c', d)

so its action on h produces a heteromorphism from c' to d, which we can call the composition h \circ f of a heteromorphism h with a morphism f. Similarly, a morphism in \mathbb{D}:

g\colon d \to d'

can be composed with h by lifting (id_c, g).

In Haskell, this new composition would be implemented by applying dimap f id to precompose p c d with

f :: c' -> c

and dimap id g to postcompose it with

g :: d -> d'

This is how we can use a profunctor to glue together two categories. Two categories connected by a profunctor form a new category known as their collage.

A given profunctor provides unidirectional flow of heteromorphisms from \mathbb{C} to \mathbb{D}, so there is no opportunity to compose two heteromorphisms.

Profunctors As Relations

The opportunity to compose heteromorphisms arises when we decide to glue more than two categories. The clue as how to proceed comes from yet another interpretation of profunctors: as proof-relevant relations. In classical logic, a relation between sets assigns a Boolean true or false to each pair of elements. The elements are either related or not, period. In proof-relevant logic, we are not only interested in whether something is true, but also in gathering witnesses to the proofs. So, instead of assigning a single Boolean to each pair of elements, we assign a whole set. If the set is empty, the elements are unrelated. If it’s non-empty, each element is a separate witness to the relation.

This definition of a relation can be generalized to any category. In fact there is already a natural relation between objects in a category–the one defined by hom-sets. Two objects a and b are related this way if the hom-set C(a, b) is non-empty. Each morphism in C(a, b) serves as a witness to this relation.

With profunctors, we can define proof-relevant relations between objects that are taken from different categories. Object c in \mathbb{C} is related to object d in \mathbb{D} if P(c, d) is a non-empty set. Moreover, each element of this set serves as a witness for the relation. Because of functoriality of P, this relation is compatible with the categorical structure, that is, it composes nicely with the relation defined by hom-sets.

In general, a composition of two relations P and Q, denoted by P \circ Q is defined as a path between objects. Objects a and c are related if there is a go-between object b such that both P(a, b) and Q(b, c) are non-empty. As a witness of this relation we can pick any pair of elements, one from P(a, b) and one from Q(b, c).

By convention, a profunctor P(a, b) is drawn as an arrow (often crossed) from b to a, a \nleftarrow b.

Composition of profunctors/relations

Profunctor Composition

To create a set of all witnesses of P \circ Q we have to sum over all possible intermediate objects and all pairs of witnesses. Roughly speaking, such a sum (modulo some identifications) is expressed categorically as a coend:

(P \circ Q)(a, c) = \int^b P(a, b) \times Q(b, c)

As a refresher, a coend of a profunctor P is a set \int^a P(a, a) equipped with a family of injections

i_x \colon P(x, x) \to \int^a P(a, a)

that is universal in the sense that, for any other set s and a family:

\alpha_x \colon P(x, x) \to s

there is a unique function h that factorizes them all:

\alpha_x = h \circ i_x

Universal property of a coend

Profunctor composition can be translated into pseudo-Haskell as:

type Procompose q p a c = exists b. (p a b, q b c)

where the coend is encoded as an existential data type. The actual implementation (again, see Edward Kmett’s Data.Profunctor.Composition) is:

data Procompose q p a c where
  Procompose :: q b c -> p a b -> Procompose q p a c

The existential quantifier is expressed in terms of a GADT (Generalized Algebraic Data Type), with the free occurrence of b inside the data constructor.

Einstein’s Convention

By now you might be getting lost juggling the variances of objects appearing in those formulas. The coend variable, for instance, must appear under the integral sign once in the covariant and once in the contravariant position, and the variances on the right must match the variances on the left. Fortunately, there is a precedent in a different branch of mathematics, tensor calculus in vector spaces, with the kind of notation that takes care of variances. Einstein coopted and expanded this notation in his theory of relativity. Let’s see if we can adapt this technique to the calculus of profunctors.

The trick is to write contravariant indices as superscripts and the covariant ones as subscripts. So, from now on, we’ll write the components of a profunctor p (we’ll switch to lower case to be compatible with Haskell) as p^c\,_d. Einstein also came up with a clever convention: implicit summation over a repeated index. In the case of profunctors, the summation corresponds to taking a coend. In this notation, a coend over a profunctor p looks like a trace of a tensor:

p^a\,_a = \int^a p(a, a)

The composition of two profunctors becomes:

(p \circ q)^a\, _c = p^a\,_b \, q^b\,_c = \int^b p(a, b) \times q(b, c)

The summation convention applies only to adjacent indices. When they are separated by an explicit product sign (or any other operator), the coend is not assumed, as in:

p^a\,_b \times q^b\,_c

(no summation).

The hom-functor in a category \mathbb{C} is also a profunctor, so it can be notated appropriately:

C^a\,_b = C(a, b)

The co-Yoneda lemma (see Ninja Yoneda) becomes:

C^c\,_{c'}\,p^{c'}\,_d \cong p^c\,_d \cong p^c\,_{d'}\,D^{d'}\,_d

suggesting that the hom-functors C^c\,_{c'} and D^{d'}\,_d behave like Kronecker deltas (in tensor-speak) or unit matrices. Here, the profunctor p spans two categories

p \colon \mathbb{C}^{op}\times \mathbb{D} \to Set

The lifting of morphisms:

f\colon c' \to c
g\colon d \to d'

can be written as:

p^f\,_g \colon p^c\,_d \to p^{c'}\,_{d'}

There is one more useful identity that deals with mapping out from a coend. It’s the consequence of the fact that the hom-functor is continuous. It means that it maps (co-) limits to limits. More precisely, since the hom-functor is contravariant in the first variable, when we fix the target object, it maps colimits in the first variable to limits. (It also maps limits to limits in the second variable). Since a coend is a colimit, and an end is a limit, continuity leads to the following identity:

Set(\int^c p(c, c), s) \cong \int_c Set(p(c, c), s)

for any set s. Programmers know this identity as a generalization of case analysis: a function from a sum type is a product of functions (one function per case). If we interpret the coend as an existential quantifier, the end is equivalent to a universal quantifier.

Let’s apply this identity to the mapping out from a composition of two profunctors:

p^a\,_b \, q^b\,_c \to s = Set\big(\int^b p(a, b) \times q(b, c), s\big)

This is isomorphic to:

\int_b Set\Big(p(a,b) \times q(b, c), s\Big)

or, after currying (using the product/exponential adjunction),

\int_b Set\Big(p(a, b), q(b, c) \to s\Big)

This gives us the mapping out formula:

p^a\,_b \, q^b\,_c \to s \cong p^a\,_b \to q^b\,_c \to s

with the right hand side natural in b. Again, we don’t perform implicit summation on the right, where the repeated indices are separated by an arrow. There, the repeated index b is universally quantified (through the end), giving rise to a natural transformation.

Bicategory Prof

Since profunctors can be composed using the coend formula, it’s natural to ask if there is a category in which they work as morphisms. The only problem is that profunctor composition satisfies the associativity and unit laws (see the co-Yoneda lemma above) only up to isomorphism. Not to worry, there is a name for that: a bicategory. In a bicategory we have objects, which are called 0-cells; morphisms, which are called 1-cells; and morphisms between morphisms, which are called 2-cells. When we say that categorical laws are satisfied up to isomorphism, it means that there is an invertible 2-cell that maps one side of the law to another.

The bicategory Prof has categories as 0-cells, profunctors as 1-cells, and natural transformations as 2-cells. A natural transformation \alpha between profunctors p and q

\alpha \colon p \Rightarrow q

has components that are functions:

\alpha^c\,_d \colon p^c\,_d \to q^c\,_d

satisfying the usual naturality conditions. Natural transformations between profunctors can be composed as functions (this is called vertical composition). In fact 2-cells in any bicategory are composable, and there always is a unit 2-cell. It follows that 1-cells between any two 0-cells form a category called the hom-category.

But there is another way of composing 2-cells that’s called horizontal composition. In Prof, this horizontal composition is not the usual horizontal composition of natural transformations, because composition of profunctors is not the usual composition of functors. We have to construct a natural transformation between one composition of profuntors, say p^a\,_b \, q^b\,_c and another, r^a\,_b \, s^b\,_c, having at our disposal two natural transformations:

\alpha \colon p \Rightarrow r

\beta \colon q \Rightarrow s

The construction is a little technical, so I’m moving it to the appendix. We will denote such horizontal composition as:

(\alpha \circ \beta)^a\,_c \colon p^a\,_b \, q^b\,_c \to r^a\,_b \, s^b\,_c

If one of the natural transformations is an identity natural transformation, say, from p^a\,_b to p^a\,_b, horizontal composition is called whiskering and can be written as:

(p \circ \beta)^a\,_c \colon p^a\,_b \, q^b\,_c \to p^a\,_b \, s^b\,_c

Promonads

The fact that a monad is a monoid in the category of endofunctors is a lucky accident. That’s because, in general, a monad can be defined in any bicategory, and Cat just happens to be a (strict) bicategory. It has (small) categories as 0-cells, functors as 1-cells, and natural transformations as 2-cells. A monad is defined as a combination of a 0-cell (you need a category to define a monad), an endo-1-cell (that would be an endofunctor in that category), and two 2-cells. These 2-cells are variably called multiplication and unit, \mu and \eta, or join and return.

Since Prof is a bicategory, we can define a monad in it, and call it a promonad. A promonad consists of a 0-cell C, which is a category; an endo-1-cell p, which is a profunctor in that category; and two 2-cells, which are natural transformations:

\mu^a\,_b \colon p^a\,_c \, p^c\,_b \to p^a\,_b

\eta^a\,_b \colon C^a\,_b \to p^a\,_b

Remember that C^a\,_b is the hom-profunctor in the category C which, due to co-Yoneda, happens to be the unit of profunctor composition.

Programmers might recognize elements of the Haskell Arrow in it (see my blog post on monoids).

We can apply the mapping-out identity to the definition of multiplication and get:

\mu^a\,_b \colon p^a\,_c \to p^c\,_b \to p^a\,_b

Notice that this looks very much like composition of heteromorphisms. Moreover, the monadic unit \eta maps regular morphisms to heteromorphisms. We can then construct a new category, whose objects are the same as the objects of \mathbb{C}, with hom-sets given by the profunctor p. That is, a hom set from a to b is the set p^a\,_b. We can define an identity-on-object functor J from \mathbb{C} to that category, whose action on hom-sets is given by \eta.

Interestingly, this construction also works in the opposite direction (as was brought to my attention by Alex Campbell). Any indentity-on-objects functor defines a promonad. Indeed, given a functor J, we can always turn it into a profunctor:

p(c, d) = D(J\, c, J\, d)

In Einstein notation, this reads:

p^c\,_d = D^{J\, c}\,_{J\, d}

Since J is identity on objects, the composition of morphisms in D can be used to define the composition of heteromorphisms. This, in turn, can be used to define \mu, thus showing that p is a promonad on \mathbb{C}.

Conclusion

I realize that I have touched upon some pretty advanced topics in category theory, like bicategories and promonads, so it’s a little surprising that these concepts can be illustrated in Haskell, some of them being present in popular libraries, like the Arrow library, which has applications in functional reactive programming.

I’ve been experimenting with applying Einstein’s summation convention to profunctors, admittedly with mixed results. This is definitely work in progress and I welcome suggestions to improve it. The main problem is that we sometimes need to apply the sum (coend), and at other times the product (end) to repeated indices. This is in particular awkward in the formulation of the mapping out property. I suggest separating the non-summed indices with product signs or arrows but I’m not sure how well this will work.

Appendix: Horizontal Composition in Prof

We have at our disposal two natural transformations:

\alpha \colon p \Rightarrow r

\beta \colon q \Rightarrow s

and the following coend, which is the composition of the profunctors p and q:

\int^b p(a, b) \times q(b, c)

Our goal is to construct an element of the target coend:

\int^b r(a, b) \times s(b, c)

Horizontal composition of 2-cells

To construct an element of a coend, we need to provide just one element of r(a, b') \times s(b', c) for some b'. We’ll look for a function that would construct such an element in the following hom-set:

Set\Big(\int^b p(a, b) \times q(b, c), r(a, b') \times s(b', c)\Big)

Using Einstein notation, we can write it as:

p^a\,_b \, q^b\,_c \to r^a\,_{b'} \times s^{b'}\,_c

and then use the mapping out property:

p^a\,_b \to q^b\,_c \to r^a\,_{b'} \times s^{b'}\,_c

We can pick b' equal to b and implement the function using the components of the two natural transformations, \alpha^a\,_{b} \times \beta^{b}\,_c.

Of course, this is how a programmer might think of it. A mathematician will use the universal property of the coend (p \circ q)^a\,_c, as in the diagram below (courtesy Alex Campbell).

Horizontal composition using the universal property of a coend

In Haskell, we can define a natural transformation between two (endo-) profunctors as a polymorphic function:

newtype PNat p q = PNat (forall a b. p a b -> q a b)

Horizontal composition is then given by:

horPNat :: PNat p r -> PNat q s -> Procompose p q a c
        -> Procompose r s a c
horPNat (PNat alpha) (PNat beta) (Procompose pbc qdb) = 
  Procompose (alpha pbc) (beta qdb)

Acknowledgment

I’m grateful to Alex Campbell from Macquarie University in Sydney for extensive help with this blog post.

Further Reading

 

December 20, 2018

Open Season on Hylomorphisms

Posted by Bartosz Milewski under Category Theory, Functional Programming, Haskell, Programming
[16] Comments 

Yes, it’s this time of the year again! I started a little tradition a year ago with Stalking a Hylomorphism in the Wild. This year I was reminded of the Advent of Code by a tweet with this succint C++ program:

This piece of code is probably unreadable to a regular C++ programmer, but makes perfect sense to a Haskell programmer.

Here’s the description of the problem: You are given a list of equal-length strings. Every string is different, but two of these strings differ only by one character. Find these two strings and return their matching part. For instance, if the two strings were “abcd” and “abxd”, you would return “abd”.

What makes this problem particularly interesting is its potential application to a much more practical task of matching strands of DNA while looking for mutations. I decided to explore the problem a little beyond the brute force approach. And, of course, I had a hunch that I might encounter my favorite wild beast–the hylomorphism.

Brute force approach

First things first. Let’s do the boring stuff: read the file and split it into lines, which are the strings we are supposed to process. So here it is:

main = do
  txt <- readFile "day2.txt"
  let cs = lines txt
  print $ findMatch cs

The real work is done by the function findMatch, which takes a list of strings and produces the answer, which is a single string.

findMatch :: [String] -> String

First, let’s define a function that calculates the distance between any two strings.

distance :: (String, String) -> Int

We’ll define the distance as the count of mismatched characters.

Here’s the idea: We have to compare strings (which, let me remind you, are of equal length) character by character. Strings are lists of characters. The first step is to take two strings and zip them together, producing a list of pairs of characters. In fact we can combine the zipping with the next operation–in this case, comparison for inequality, (/=)–using the library function zipWith. However, zipWith is defined to act on two lists, and we will want it to act on a pair of lists–a subtle distinction, which can be easily overcome by applying uncurry:

uncurry :: (a -> b -> c) -> ((a, b) -> c)

which turns a function of two arguments into a function that takes a pair. Here’s how we use it:

uncurry (zipWith (/=))

The comparison operator (/=) produces a Boolean result, True or False. We want to count the number of differences, so we’ll covert True to one, and False to zero:

fromBool :: Num a => Bool -> a
fromBool False = 0
fromBool True  = 1

(Notice that such subtleties as the difference between Bool and Int are blisfully ignored in C++.)

Finally, we’ll sum all the ones using sum. Altogether we have:

distance = sum . fmap fromBool . uncurry (zipWith (/=))

Now that we know how to find the distance between any two strings, we’ll just apply it to all possible pairs of strings. To generate all pairs, we’ll use list comprehension:

let ps = [(s1, s2) | s1 <- ss, s2 <- ss]

(In C++ code, this was done by cartesian_product.)

Our goal is to find the pair whose distance is exactly one. To this end, we’ll apply the appropriate filter:

filter ((== 1) . distance) ps

For our purposes, we’ll assume that there is exactly one such pair (if there isn’t one, we are willing to let the program fail with a fatal exception).

(s, s') = head $ filter ((== 1) . distance) ps

The final step is to remove the mismatched character:

filter (uncurry (==)) $ zip s s'

We use our friend uncurry again, because the equality operator (==) expects two arguments, and we are calling it with a pair of arguments. The result of filtering is a list of identical pairs. We’ll fmap fst to pick the first components.

findMatch :: [String] -> String
findMatch ss = 
  let ps = [(s1, s2) | s1 <- ss, s2 <- ss]
      (s, s') = head $ filter ((== 1) . distance) ps
  in fmap fst $ filter (uncurry (==)) $ zip s s'

This program produces the correct result and we could stop right here. But that wouldn’t be much fun, would it? Besides, it’s possible that other algorithms could perform better, or be more flexible when applied to a more general problem.

Data-driven approach

The main problem with our brute-force approach is that we are comparing everything with everything. As we increase the number of input strings, the number of comparisons grows like a factorial. There is a standard way of cutting down on the number of comparison: organizing the input into a neat data structure.

We are comparing strings, which are lists of characters, and list comparison is done recursively. Assume that you know that two strings share a prefix. Compare the next character. If it’s equal in both strings, recurse. If it’s not, we have a single character fault. The rest of the two strings must now match perfectly to be considered a solution. So the best data structure for this kind of algorithm should batch together strings with equal prefixes. Such a data structure is called a prefix tree, or a trie (pronounced try).

At every level of our prefix tree we’ll branch based on the current character (so the maximum branching factor is, in our case, 26). We’ll record the character, the count of strings that share the prefix that led us there, and the child trie storing all the suffixes.

data Trie = Trie [(Char, Int, Trie)]
  deriving (Show, Eq)

Here’s an example of a trie that stores just two strings, “abcd” and “abxd”. It branches after b.

   a 2
   b 2
c 1    x 1
d 1    d 1

When inserting a string into a trie, we recurse both on the characters of the string and the list of branches. When we find a branch with the matching character, we increment its count and insert the rest of the string into its child trie. If we run out of branches, we create a new one based on the current character, give it the count one, and the child trie with the rest of the string:

insertS :: Trie -> String -> Trie
insertS t "" = t
insertS (Trie bs) s = Trie (inS bs s)
  where
    inS ((x, n, t) : bs) (c : cs) =
      if c == x 
      then (c, n + 1, insertS t cs) : bs
      else (x, n, t) : inS bs (c : cs)
    inS [] (c : cs) = [(c, 1, insertS (Trie []) cs)]

We convert our input to a trie by inserting all the strings into an (initially empty) trie:

mkTrie :: [String] -> Trie
mkTrie = foldl insertS (Trie [])

Of course, there are many optimizations we could use, if we were to run this algorithm on big data. For instance, we could compress the branches as is done in radix trees, or we could sort the branches alphabetically. I won’t do it here.

I won’t pretend that this implementation is simple and elegant. And it will get even worse before it gets better. The problem is that we are dealing explicitly with recursion in multiple dimensions. We recurse over the input string, the list of branches at each node, as well as the child trie. That’s a lot of recursion to keep track of–all at once.

Now brace yourself: We have to traverse the trie starting from the root. At every branch we check the prefix count: if it’s greater than one, we have more than one string going down, so we recurse into the child trie. But there is also another possibility: we can allow to have a mismatch at the current level. The current characters may be different but, since we allow only one mismatch, the rest of the strings have to match exactly. That’s what the function exact does. Notice that exact t is used inside foldMap, which is a version of fold that works on monoids–here, on strings.

match1 :: Trie -> [String]
match1 (Trie bs) = go bs
  where
    go :: [(Char, Int, Trie)] -> [String]
    go ((x, n, t) : bs) = 
      let a1s = if n > 1 
                then fmap (x:) $ match1 t
                else []
          a2s = foldMap (exact t) bs
          a3s = go bs -- recurse over list
      in a1s ++ a2s ++ a3s
    go [] = []
    exact t (_, _, t') = matchAll t t'

Here’s the function that finds all exact matches between two tries. It does it by generating all pairs of branches in which top characters match, and then recursing down.

matchAll :: Trie -> Trie -> [String]
matchAll (Trie bs) (Trie bs') = mAll bs bs'
  where
    mAll :: [(Char, Int, Trie)] -> [(Char, Int, Trie)] -> [String]
    mAll [] [] = [""]
    mAll bs bs' = 
      let ps = [ (c, t, t') 
               | (c,  _,  t)  <- bs
               , (c', _', t') <- bs'
               , c == c']
      in foldMap go ps
    go (c, t, t') = fmap (c:) (matchAll t t')

When mAll reaches the leaves of the trie, it returns a singleton list containing an empty string. Subsequent actions of fmap (c:) will prepend characters to this string.

Since we are expecting exactly one solution to the problem, we’ll extract it using head:

findMatch1 :: [String] -> String
findMatch1 cs = head $ match1 (mkTrie cs)

Recursion schemes

As you hone your functional programming skills, you realize that explicit recursion is to be avoided at all cost. There is a small number of recursive patterns that have been codified, and they can be used to solve the majority of recursion problems (for some categorical background, see F-Algebras). Recursion itself can be expressed in Haskell as a data structure: a fixed point of a functor:

newtype Fix f = In { out :: f (Fix f) }

In particular, our trie can be generated from the following functor:

data TrieF a = TrieF [(Char, a)]
  deriving (Show, Functor)

Notice how I have replaced the recursive call to the Trie type constructor with the free type variable a. The functor in question defines the structure of a single node, leaving holes marked by the occurrences of a for the recursion. When these holes are filled with full blown tries, as in the definition of the fixed point, we recover the complete trie.

I have also made one more simplification by getting rid of the Int in every node. This is because, in the recursion scheme I’m going to use, the folding of the trie proceeds bottom-up, rather than top-down, so the multiplicity information can be passed upwards.

The main advantage of recursion schemes is that they let us use simpler, non-recursive building blocks such as algebras and coalgebras. Let’s start with a simple coalgebra that lets us build a trie from a list of strings. A coalgebra is a fancy name for a particular type of function:

type Coalgebra f x = x -> f x

Think of x as a type for a seed from which one can grow a tree. A colagebra tells us how to use this seed to create a single node described by the functor f and populate it with (presumably smaller) seeds. We can then pass this coalgebra to a simple algorithm, which will recursively expand the seeds. This algorithm is called the anamorphism:

ana :: Functor f => Coalgebra f a -> a -> Fix f
ana coa = In . fmap (ana coa) . coa

Let’s see how we can apply it to the task of building a trie. The seed in our case is a list of strings (as per the definition of our problem, we’ll assume they are all equal length). We start by grouping these strings into bunches of strings that start with the same character. There is a library function called groupWith that does exactly that. We have to import the right library:

import GHC.Exts (groupWith)

This is the signature of the function:

groupWith :: Ord b => (a -> b) -> [a] -> [[a]]

It takes a function a -> b that converts each list element to a type that supports comparison (as per the typeclass Ord), and partitions the input into lists that compare equal under this particular ordering. In our case, we are going to extract the first character from a string using head and bunch together all strings that share that first character.

let sss = groupWith head ss

The tails of those strings will serve as seeds for the next tier of the trie. Eventually the strings will be shortened to nothing, triggering the end of recursion.

fromList :: Coalgebra TrieF [String]
fromList ss =
  -- are strings empty? (checking one is enough)
  if null (head ss) 
  then TrieF [] -- leaf
  else
    let sss = groupWith head ss
    in TrieF $ fmap mkBranch sss

The function mkBranch takes a bunch of strings sharing the same first character and creates a branch seeded with the suffixes of those strings.

mkBranch :: [String] -> (Char, [String])
mkBranch sss =
  let c = head (head sss) -- they're all the same
  in (c, fmap tail sss)

Notice that we have completely avoided explicit recursion.

The next step is a little harder. We have to fold the trie. Again, all we have to define is a step that folds a single node whose children have already been folded. This step is defined by an algebra:

type Algebra f x = f x -> x

Just as the type x described the seed in a coalgebra, here it describes the accumulator–the result of the folding of a recursive data structure.

We pass this algebra to a special algorithm called a catamorphism that takes care of the recursion:

cata :: Functor f => Algebra f a -> Fix f -> a
cata alg = alg . fmap (cata alg) . out

Notice that the folding proceeds from the bottom up: the algebra assumes that all the children have already been folded.

The hardest part of designing an algebra is figuring out what information needs to be passed up in the accumulator. We obviously need to return the final result which, in our case, is the list of strings with one mismatched character. But when we are in the middle of a trie, we have to keep in mind that the mismatch may still happen above us. So we also need a list of strings that may serve as suffixes when the mismatch occurs. We have to keep them all, because they might be matched later with strings from other branches.

In other words, we need to be accumulating two lists of strings. The first list accumulates all suffixes for future matching, the second accumulates the results: strings with one mismatch (after the mismatch has been removed). We therefore should implement the following algebra:

Algebra TrieF ([String], [String])

To understand the implementation of this algebra, consider a single node in a trie. It’s a list of branches, or pairs, whose first component is the current character, and the second a pair of lists of strings–the result of folding a child trie. The first list contains all the suffixes gathered from lower levels of the trie. The second list contains partial results: strings that were matched modulo single-character defect.

As an example, suppose that you have a node with two branches:

[ ('a', (["bcd", "efg"], ["pq"]))
, ('x', (["bcd"],        []))]

First we prepend the current character to strings in both lists using the function prep with the following signature:

prep :: (Char, ([String], [String])) -> ([String], [String])

This way we convert each branch to a pair of lists. 

[ (["abcd", "aefg"], ["apq"])
, (["xbcd"],         [])]

We then merge all the lists of suffixes and, separately, all the lists of partial results, across all branches. In the example above, we concatenate the lists in the two columns.

(["abcd", "aefg", "xbcd"], ["apq"])

Now we have to construct new partial results. To do this, we create another list of accumulated strings from all branches (this time without prefixing them):

ss = concat $ fmap (fst . snd) bs

In our case, this would be the list:

["bcd", "efg", "bcd"]

To detect duplicate strings, we’ll insert them into a multiset, which we’ll implement as a map. We need to import the appropriate library:

import qualified Data.Map as M

and define a multiset Counts as:

type Counts a = M.Map a Int

Every time we add a new item, we increment the count:

add :: Ord a => Counts a -> a -> Counts a
add cs c = M.insertWith (+) c 1 cs

To insert all strings from a list, we use a fold:

mset = foldl add M.empty ss

We are only interested in items that have multiplicity greater than one. We can filter them and extract their keys:

dups = M.keys $ M.filter (> 1) mset

Here’s the complete algebra:

accum :: Algebra TrieF ([String], [String])
accum (TrieF []) = ([""], [])
accum (TrieF bs) = -- b :: (Char, ([String], [String]))
    let -- prepend chars to string in both lists
        pss = unzip $ fmap prep bs
        (ss1, ss2) = both concat pss
        -- find duplicates
        ss = concat $ fmap (fst . snd) bs
        mset = foldl add M.empty ss
        dups = M.keys $ M.filter (> 1) mset
     in (ss1, dups ++ ss2)
  where
      prep :: (Char, ([String], [String])) -> ([String], [String])
      prep (c, pss) = both (fmap (c:)) pss

I used a handy helper function that applies a function to both components of a pair:

both :: (a -> b) -> (a, a) -> (b, b)
both f (x, y) = (f x, f y)

And now for the grand finale: Since we create the trie using an anamorphism only to immediately fold it using a catamorphism, why don’t we cut the middle person? Indeed, there is an algorithm called the hylomorphism that does just that. It takes the algebra, the coalgebra, and the seed, and returns the fully charged accumulator. 

hylo :: Functor f => Algebra f a -> Coalgebra f b -> b -> a
hylo alg coa = alg . fmap (hylo alg coa) . coa

And this is how we extract and print the final result:

print $ head $ snd $ hylo accum fromList cs

Conclusion

The advantage of using the hylomorphism is that, because of Haskell’s laziness, the trie is never wholly constructed, and therefore doesn’t require large amounts of memory. At every step enough of the data structure is created as is needed for immediate computation; then it is promptly released. In fact, the definition of the data structure is only there to guide the steps of the algorithm. We use a data structure as a control structure. Since data structures are much easier to visualize and debug than control structures, it’s almost always advantageous to use them to drive computation.

In fact, you may notice that, in the very last step of the computation, our accumulator recreates the original list of strings (actually, because of laziness, they are never fully reconstructed, but that’s not the point). In reality, the characters in the strings are never copied–the whole algorithm is just a choreographed dance of internal pointers, or iterators. But that’s exactly what happens in the original C++ algorithm. We just use a higher level of abstraction to describe this dance.

I haven’t looked at the performance of various implementations. Feel free to test it and report the results. The code is available on github.

Acknowledgments

I’m grateful to the participants of the Seattle Haskell Users’ Group for many helpful comments during my presentation.

 

October 12, 2018

Trading FunLists at a Bazaar with Yoneda

Posted by Bartosz Milewski under Category Theory, Functional Programming, Haskell, Programming
[5] Comments 

There is a lot of folklore about various data types that pop up in discussions about lenses. For instance, it’s known that FunList and Bazaar are equivalent, although I haven’t seen a proof of that. Since both data structures appear in the context of Traversable, which is of great interest to me, I decided to do some research. In particular, I was interested in translating these data structures into constructs in category theory. This is a continuation of my previous blog posts on free monoids and free applicatives. Here’s what I have found out:

  • FunList is a free applicative generated by the Store functor. This can be shown by expressing the free applicative construction using Day convolution.
  • Using Yoneda lemma in the category of applicative functors I can show that Bazaar is equivalent to FunList

Let’s start with some definitions. FunList was first introduced by Twan van Laarhoven in his blog. Here’s a (slightly generalized) Haskell definition:

data FunList a b t = Done t 
                   | More a (FunList a b (b -> t))

It’s a non-regular inductive data structure, in the sense that its data constructor is recursively called with a different type, here the function type b->t. FunList is a functor in t, which can be written categorically as:

L_{a b} t = t + a \times L_{a b} (b \to t)

where b \to t is a shorthand for the hom-set Set(b, t).

Strictly speaking, a recursive data structure is defined as an initial algebra for a higher-order functor. I will show that the higher order functor in question can be written as:

A_{a b} g = I + \sigma_{a b} \star g

where \sigma_{a b} is the (indexed) store comonad, which can be written as:

\sigma_{a b} s = \Delta_a s \times C(b, s)

Here, \Delta_a is the constant functor, and C(b, -) is the hom-functor. In Haskell, this is equivalent to:

newtype Store a b s = Store (a, b -> s)

The standard (non-indexed) Store comonad is obtained by identifying a with b and it describes the objects of the slice category C/s (morphisms are functions f : a \to a' that make the obvious triangles commute).

If you’ve read my previous blog posts, you may recognize in A_{a b} the functor that generates a free applicative functor (or, equivalently, a free monoidal functor). Its fixed point can be written as:

L_{a b} = I + \sigma_{a b} \star L_{a b}

The star stands for Day convolution–in Haskell expressed as an existential data type:

data Day f g s where
  Day :: f a -> g b -> ((a, b) -> s) -> Day f g s

Intuitively, L_{a b} is a “list of” Store functors concatenated using Day convolution. An empty list is the identity functor, a one-element list is the Store functor, a two-element list is the Day convolution of two Store functors, and so on…

In Haskell, we would express it as:

data FunList a b t = Done t 
                   | More ((Day (Store a b) (FunList a b)) t)

To show the equivalence of the two definitions of FunList, let’s expand the definition of Day convolution inside A_{a b}:

(A_{a b} g) t = t + \int^{c d} (\Delta_b c \times C(a, c)) \times g d \times C(c \times d, t)

The coend \int^{c d} corresponds, in Haskell, to the existential data type we used in the definition of Day.

Since we have the hom-functor C(a, c) under the coend, the first step is to use the co-Yoneda lemma to “perform the integration” over c, which replaces c with a everywhere. We get:

t + \int^d \Delta_b a \times g d \times C(a \times d, t)

We can then evaluate the constant functor and use the currying adjunction:

C(a \times d, t) \cong C(d, a \to t)

to get:

t + \int^d b \times g d \times C(d, a \to t)

Applying the co-Yoneda lemma again, we replace d with a \to t:

t + b \times g (a \to t)

This is exactly the functor that generates FunList. So FunList is indeed the free applicative generated by Store.

All transformations in this derivation were natural isomorphisms.

Now let’s switch our attention to Bazaar, which can be defined as:

type Bazaar a b t = forall f. Applicative f => (a -> f b) -> f t

(The actual definition of Bazaar in the lens library is even more general–it’s parameterized by a profunctor in place of the arrow in a -> f b.)

The universal quantification in the definition of Bazaar immediately suggests the application of my favorite double Yoneda trick in the functor category: The set of natural transformations (morphisms in the functor category) between two functors (objects in the functor category) is isomorphic, through Yoneda embedding, to the following end in the functor category:

Nat(h, g) \cong \int_{f \colon [C, Set]} Set(Nat(g, f), Nat(h, f))

The end is equivalent (modulo parametricity) to Haskell forall. Here, the sets of natural transformations between pairs of functors are just hom-functors in the functor category and the end over f is a set of higher-order natural transformations between them.

In the double Yoneda trick we carefully select the two functors g and h to be either representable, or somehow related to representables.

The universal quantification in Bazaar is limited to applicative functors, so we’ll pick our two functors to be free applicatives. We’ve seen previously that the higher-order functor that generates free applicatives has the form:

F g = Id + g \star F g

Here’s the version of the Yoneda embedding in which f varies over all applicative functors in the category App, and g and h are arbitrary functors in [C, Set]:

App(F h, F g) \cong \int_{f \colon App} Set(App(F g, f), App(F h, f))

The free functor F is the left adjoint to the forgetful functor U:

App(F g, f) \cong [C, Set](g, U f)

Using this adjunction, we arrive at:

[C, Set](h, U (F g)) \cong \int_{f \colon App} Set([C, Set](g, U f), [C, Set](h, U f))

We’re almost there–we just need to carefuly pick the functors g and h. In order to arrive at the definition of Bazaar we want:

g = \sigma_{a b} = \Delta_a \times C(b, -)

h = C(t, -)

The right hand side becomes:

\int_{f \colon App} Set\big(\int_c Set (\Delta_a c \times C(b, c), (U f) c)), \int_c Set (C(t, c), (U f) c)\big)

where I represented natural transformations as ends. The first term can be curried:

Set \big(\Delta_a c \times C(b, c), (U f) c)\big) \cong Set\big(C(b, c), \Delta_a c \to (U f) c \big)

and the end over c can be evaluated using the Yoneda lemma. So can the second term. Altogether, the right hand side becomes:

\int_{f \colon App} Set\big(a \to (U f) b)), (U f) t)\big)

In Haskell notation, this is just the definition of Bazaar:

forall f. Applicative f => (a -> f b) -> f t

The left hand side can be written as:

\int_c Set(h c, (U (F g)) c)

Since we have chosen h to be the hom-functor C(t, -), we can use the Yoneda lemma to “perform the integration” and arrive at:

(U (F g)) t

With our choice of g = \sigma_{a b}, this is exactly the free applicative generated by Store–in other words, FunList.

This proves the equivalence of Bazaar and FunList. Notice that this proof is only valid for Set-valued functors, although a generalization to the enriched setting is relatively straightforward.

There is another family of functors, Traversable, that uses universal quantification over applicatives:

class (Functor t, Foldable t) => Traversable t where
  traverse :: forall f. Applicative f => (a -> f b) -> t a -> f (t b)

The same double Yoneda trick can be applied to it to show that it’s related to Bazaar. There is, however, a much simpler derivation, suggested to me by Derek Elkins, by changing the order of arguments:

traverse :: t a -> (forall f. Applicative f => (a -> f b) -> f (t b))

which is equivalent to:

traverse :: t a -> Bazaar a b (t b)

In view of the equivalence between Bazaar and FunList, we can also write it as:

traverse :: t a -> FunList a b (t b)

Note that this is somewhat similar to the definition of toList:

toList :: Foldable t => t a -> [a]

In a sense, FunList is able to freely accumulate the effects from traversable, so that they can be interpreted later.

Acknowledgments

I’m grateful to Edward Kmett and Derek Elkins for many discussions and valuable insights.

 

August 20, 2018

Recursion Schemes for Higher Algebras

Posted by Bartosz Milewski under Category Theory, Functional Programming, Haskell, Monads, Programming
[4] Comments 

Abstract

The use of free monads, free applicatives, and cofree comonads lets us separate the construction of (often effectful or context-dependent) computations from their interpretation. In this paper I show how the ad hoc process of writing interpreters for these free constructions can be systematized using the language of higher order algebras (coalgebras) and catamorphisms (anamorphisms).

Introduction

Recursive schemes [meijer] are an example of successful application of concepts from category theory to programming. The idea is that recursive data structures can be defined as initial algebras of functors. This allows a separation of concerns: the functor describes the local shape of the data structure, and the fixed point combinator builds the recursion. Operations over data structures can be likewise separated into shallow, non-recursive computations described by algebras, and generic recursive procedures described by catamorphisms. In this way, data structures often replace control structures in driving computations.

Since functors also form a category, it’s possible to define functors acting on functors. Such higher order functors show up in a number of free constructions, notably free monads, free applicatives, and cofree comonads. These free constructions have good composability properties and they provide means of separating the creation of effectful computations from their interpretation.

This paper’s contribution is to systematize the construction of such interpreters. The idea is that free constructions arise as fixed points of higher order functors, and therefore can be approached with the same algebraic machinery as recursive data structures, only at a higher level. In particular, interpreters can be constructed as catamorphisms or anamorphisms of higher order algebras/coalgebras.

Initial Algebras and Catamorphisms

The canonical example of a data structure that can be described as an initial algebra of a functor is a list. In Haskell, a list can be defined recursively:

data List a = Nil | Cons a (List a)

There is an underlying non-recursive functor:

data ListF a x = NilF | ConsF a x
instance Functor (ListF a) where
  fmap f NilF = NilF
  fmap f (ConsF a x) = ConsF a (f x)

Once we have a functor, we can define its algebras. An algebra consist of a carrier c and a structure map (evaluator). An algebra can be defined for an arbitrary functor f:

type Algebra f c = f c -> c

Here’s an example of a simple list algebra, with Int as its carrier:

sum :: Algebra (ListF Int) Int
sum NilF = 0
sum (ConsF a c) = a + c

Algebras for a given functor form a category. The initial object in this category (if it exists) is called the initial algebra. In Haskell, we call the carrier of the initial algebra Fix f. Its structure map is a function:

f (Fix f) -> Fix f

By Lambek’s lemma, the structure map of the initial algebra is an isomorphism. In Haskell, this isomorphism is given by a pair of functions: the constructor In and the destructor out of the fixed point combinator:

newtype Fix f = In { out :: f (Fix f) }

When applied to the list functor, the fixed point gives rise to an alternative definition of a list:

type List a = Fix (ListF a)

The initiality of the algebra means that there is a unique algebra morphism from it to any other algebra. This morphism is called a catamorphism and, in Haskell, can be expressed as:

cata :: Functor f => Algebra f a -> Fix f -> a
cata alg = alg . fmap (cata alg) . out

A list catamorphism is known as a fold. Since the list functor is a sum type, its algebra consists of a value—the result of applying the algebra to NilF—and a function of two variables that corresponds to the ConsF constructor. You may recognize those two as the arguments to foldr:

foldr :: (a -> c -> c) -> c -> [a] -> c

The list functor is interesting because its fixed point is a free monoid. In category theory, monoids are special objects in monoidal categories—that is categories that define a product of two objects. In Haskell, a pair type plays the role of such a product, with the unit type as its unit (up to isomorphism).

As you can see, the list functor is the sum of a unit and a product. This formula can be generalized to an arbitrary monoidal category with a tensor product 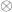\otimes and a unit 1:

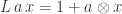
L\, a\, x = 1 + a \otimes x

Its initial algebra is a free monoid .

Higher Algebras

In category theory, once you performed a construction in one category, it’s easy to perform it in another category that shares similar properties. In Haskell, this might require reimplementing the construction.

We are interested in the category of endofunctors, where objects are endofunctors and morphisms are natural transformations. Natural transformations are represented in Haskell as polymorphic functions:

type f :~> g = forall a. f a -> g a
infixr 0 :~>

In the category of endofunctors we can define (higher order) functors, which map functors to functors and natural transformations to natural transformations:

class HFunctor hf where
  hfmap :: (g :~> h) -> (hf g :~> hf h)
  ffmap :: Functor g => (a -> b) -> hf g a -> hf g b

The first function lifts a natural transformation; and the second function, ffmap, witnesses the fact that the result of a higher order functor is again a functor.

An algebra for a higher order functor hf consists of a functor f (the carrier object in the functor category) and a natural transformation (the structure map):

type HAlgebra hf f = hf f :~> f

As with regular functors, we can define an initial algebra using the fixed point combinator for higher order functors:

newtype FixH hf a = InH { outH :: hf (FixH hf) a }

Similarly, we can define a higher order catamorphism:

hcata :: HFunctor h => HAlgebra h f -> FixH h :~> f
hcata halg = halg . hfmap (hcata halg) . outH

The question is, are there any interesting examples of higher order functors and algebras that could be used to solve real-life programming problems?

Free Monad

We’ve seen the usefulness of lists, or free monoids, for structuring computations. Let’s see if we can generalize this concept to higher order functors.

The definition of a list relies on the monoidal structure of the underlying category. It turns out that there are multiple monoidal structures of interest that can be defined in the category of functors. The simplest one defines a product of two endofunctors as their composition. Any two endofunctors can be composed. The unit of functor composition is the identity functor.

If you picture endofunctors as containers, you can easily imagine a tree of lists, or a list of Maybes.

A monoid based on this particular monoidal structure in the endofunctor category is a monad. It’s an endofunctor m equipped with two natural transformations representing unit and multiplication:

class Monad m where
  eta :: Identity    :~> m
  mu  :: Compose m m :~> m

In Haskell, the components of these natural transformations are known as return and join.

A straightforward generalization of the list functor to the functor category can be written as:

L\, f\, g = 1 + f \circ g

or, in Haskell,

type FunctorList f g = Identity :+: Compose f g

where we used the operator :+: to define the coproduct of two functors:

data (f :+: g) e = Inl (f e) | Inr (g e)
infixr 7 :+:

Using more conventional notation, FunctorList can be written as:

data MonadF f g a = 
    DoneM a 
  | MoreM (f (g a))

We’ll use it to generate a free monoid in the category of endofunctors. First of all, let’s show that it’s indeed a higher order functor in the second argument g:

instance Functor f => HFunctor (MonadF f) where
  hfmap _   (DoneM a)  = DoneM a
  hfmap nat (MoreM fg) = MoreM $ fmap nat fg
  ffmap h (DoneM a)    = DoneM (h a)
  ffmap h (MoreM fg)   = MoreM $ fmap (fmap h) fg

In category theory, because of size issues, this functor doesn’t always have a fixed point. For most common choices of f (e.g., for algebraic data types), the initial higher order algebra for this functor exists, and it generates a free monad. In Haskell, this free monad can be defined as:

type FreeMonad f = FixH (MonadF f)

We can show that FreeMonad is indeed a monad by implementing return and bind:

instance Functor f => Monad (FreeMonad f) where
  return = InH . DoneM
  (InH (DoneM a))    >>= k = k a
  (InH (MoreM ffra)) >>= k = 
        InH (MoreM (fmap (>>= k) ffra))

Free monads have many applications in programming. They can be used to write generic monadic code, which can then be interpreted in different monads. A very useful property of free monads is that they can be composed using coproducts. This follows from the theorem in category theory, which states that left adjoints preserve coproducts (or, more generally, colimits). Free constructions are, by definition, left adjoints to forgetful functors. This property of free monads was explored by Swierstra [swierstra] in his solution to the expression problem. I will use an example based on his paper to show how to construct monadic interpreters using higher order catamorphisms.

Free Monad Example

A stack-based calculator can be implemented directly using the state monad. Since this is a very simple example, it will be instructive to re-implement it using the free monad approach.

We start by defining a functor, in which the free parameter k represents the continuation:

data StackF k  = Push Int k
               | Top (Int -> k)
               | Pop k            
               | Add k
               deriving Functor

We use this functor to build a free monad:

type FreeStack = FreeMonad StackF

You may think of the free monad as a tree with nodes that are defined by the functor StackF. The unary constructors, like Add or Pop, create linear list-like branches; but the Top constructor branches out with one child per integer.

The level of indirection we get by separating recursion from the functor makes constructing free monad trees syntactically challenging, so it makes sense to define a helper function:

liftF :: (Functor f) => f r -> FreeMonad f r
liftF fr = InH $ MoreM $ fmap (InH . DoneM) fr

With this function, we can define smart constructors that build leaves of the free monad tree:

push :: Int -> FreeStack ()
push n = liftF (Push n ())

pop :: FreeStack ()
pop = liftF (Pop ())

top :: FreeStack Int
top = liftF (Top id)

add :: FreeStack ()
add = liftF (Add ())

All these preparations finally pay off when we are able to create small programs using do notation:

calc :: FreeStack Int
calc = do
  push 3
  push 4
  add
  x <- top
  pop
  return x

Of course, this program does nothing but build a tree. We need a separate interpreter to do the calculation. We’ll interpret our program in the state monad, with state implemented as a stack (list) of integers:

type MemState = State [Int]

The trick is to define a higher order algebra for the functor that generates the free monad and then use a catamorphism to apply it to the program. Notice that implementing the algebra is a relatively simple procedure because we don’t have to deal with recursion. All we need is to case-analyze the shallow constructors for the free monad functor MonadF, and then case-analyze the shallow constructors for the functor StackF.

runAlg :: HAlgebra (MonadF StackF) MemState
runAlg (DoneM a)  = return a
runAlg (MoreM ex) = 
  case ex of
    Top  ik  -> get >>= ik  . head
    Pop  k   -> get >>= put . tail   >> k
    Push n k -> get >>= put . (n : ) >> k
    Add  k   -> do (a: b: s) <- get
                   put (a + b : s)
                   k

The catamorphism converts the program calc into a state monad action, which can be run over an empty initial stack:

runState (hcata runAlg calc) []

The real bonus is the freedom to define other interpreters by simply switching the algebras. Here’s an algebra whose carrier is the Const functor:

showAlg :: HAlgebra (MonadF StackF) (Const String)

showAlg (DoneM a) = Const "Done!"
showAlg (MoreM ex) = Const $
  case ex of
    Push n k -> 
      "Push " ++ show n ++ ", " ++ getConst k
    Top ik -> 
      "Top, " ++ getConst (ik 42)
    Pop k -> 
      "Pop, " ++ getConst k
    Add k -> 
      "Add, " ++ getConst k

Runing the catamorphism over this algebra will produce a listing of our program:

getConst $ hcata showAlg calc

> "Push 3, Push 4, Add, Top, Pop, Done!"

Free Applicative

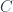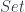There is another monoidal structure that exists in the category of functors. In general, this structure will work for functors from an arbitrary monoidal category C to Set. Here, we’ll restrict ourselves to endofunctors on 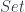Set. The product of two functors is given by Day convolution, which can be implemented in Haskell using an existential type:

data Day f g c where
  Day :: f a -> g b -> ((a, b) -> c) -> Day f g c

The intuition is that a Day convolution contains a container of some as, and another container of some bs, together with a function that can convert any pair (a, b) to c.

Day convolution is a higher order functor:

instance HFunctor (Day f) where
  hfmap nat (Day fx gy xyt) = Day fx (nat gy) xyt
  ffmap h   (Day fx gy xyt) = Day fx gy (h . xyt)

In fact, because Day convolution is symmetric up to isomorphism, it is automatically functorial in both arguments.

To complete the monoidal structure, we also need a functor that could serve as a unit with respect to Day convolution. In general, this would be the the hom-functor from the monoidal unit:

C(1, -)

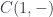
In our case, since 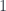1 is the singleton set, this functor reduces to the identity functor.

We can now define monoids in the category of functors with the monoidal structure given by Day convolution. These monoids are equivalent to lax monoidal functors which, in Haskell, form the class:

class Functor f => Monoidal f where
  unit  :: f ()
  (>*<) :: f x -> f y -> f (x, y)

Lax monoidal functors are equivalent to applicative functors [mcbride], as seen in this implementation of pure and <*>:

  pure  :: a -> f a
  pure a = fmap (const a) unit
  (<*>) :: f (a -> b) -> f a -> f b
  fs <*> as = fmap (uncurry ($)) (fs >*< as)

We can now use the same general formula, but with Day convolution as the product:

L\, f\, g = 1 + f \star g

to generate a free monoidal (applicative) functor:

data FreeF f g t =
      DoneF t
    | MoreF (Day f g t)

This is indeed a higher order functor:

instance HFunctor (FreeF f) where
    hfmap _ (DoneF x)     = DoneF x
    hfmap nat (MoreF day) = MoreF (hfmap nat day)
    ffmap f (DoneF x)     = DoneF (f x)
    ffmap f (MoreF day)   = MoreF (ffmap f day)

and it generates a free applicative functor as its initial algebra:

type FreeA f = FixH (FreeF f)

Free Applicative Example

The following example is taken from the paper by Capriotti and Kaposi [capriotti]. It’s an option parser for a command line tool, whose result is a user record of the following form:

data User = User
  { username :: String 
  , fullname :: String
  , uid      :: Int
  } deriving Show

A parser for an individual option is described by a functor that contains the name of the option, an optional default value for it, and a reader from string:

data Option a = Option
  { optName    :: String
  , optDefault :: Maybe a
  , optReader  :: String -> Maybe a 
  } deriving Functor

Since we don’t want to commit to a particular parser, we’ll create a parsing action using a free applicative functor:

userP :: FreeA Option User
userP  = pure User 
  <*> one (Option "username" (Just "John")  Just)
  <*> one (Option "fullname" (Just "Doe")   Just)
  <*> one (Option "uid"      (Just 0)       readInt)

where readInt is a reader of integers:

readInt :: String -> Maybe Int
readInt s = readMaybe s

and we used the following smart constructors:

one :: f a -> FreeA f a
one fa = InH $ MoreF $ Day fa (done ()) fst

done :: a -> FreeA f a
done a = InH $ DoneF a

We are now free to define different algebras to evaluate the free applicative expressions. Here’s one that collects all the defaults:

alg :: HAlgebra (FreeF Option) Maybe
alg (DoneF a) = Just a
alg (MoreF (Day oa mb f)) = 
  fmap f (optDefault oa >*< mb)

I used the monoidal instance for Maybe:

instance Monoidal Maybe where
  unit = Just ()
  Just x >*< Just y = Just (x, y)
  _ >*< _ = Nothing

This algebra can be run over our little program using a catamorphism:

parserDef :: FreeA Option a -> Maybe a
parserDef = hcata alg

And here’s an algebra that collects the names of all the options:

alg2 :: HAlgebra (FreeF Option) (Const String)
alg2 (DoneF a) = Const "."
alg2 (MoreF (Day oa bs f)) = 
  fmap f (Const (optName oa) >*< bs)

Again, this uses a monoidal instance for Const:

instance Monoid m => Monoidal (Const m) where
  unit = Const mempty
  Const a >*< Const b = Const (a  b)

We can also define the Monoidal instance for IO:

instance Monoidal IO where
  unit = return ()
  ax >*< ay = do a <- ax
                 b <- ay
                 return (a, b)

This allows us to interpret the parser in the IO monad:

alg3 :: HAlgebra (FreeF Option) IO
alg3 (DoneF a) = return a
alg3 (MoreF (Day oa bs f)) = do
    putStrLn $ optName oa
    s <- getLine
    let ma = optReader oa s
        a = fromMaybe (fromJust (optDefault oa)) ma
    fmap f $ return a >*< bs

Cofree Comonad

Every construction in category theory has its dual—the result of reversing all the arrows. The dual of a product is a coproduct, the dual of an algebra is a coalgebra, and the dual of a monad is a comonad.

Let’s start by defining a higher order coalgebra consisting of a carrier f, which is a functor, and a natural transformation:

type HCoalgebra hf f = f :~> hf f

An initial algebra is dualized to a terminal coalgebra. In Haskell, both are the results of applying the same fixed point combinator, reflecting the fact that the Lambek’s lemma is self-dual. The dual to a catamorphism is an anamorphism. Here is its higher order version:

hana :: HFunctor hf 
     => HCoalgebra hf f -> (f :~> FixH hf)
hana hcoa = InH . hfmap (hana hcoa) . hcoa

The formula we used to generate free monoids:

1 + a \otimes x

dualizes to:

1 \times a \otimes x

and can be used to generate cofree comonoids .

A cofree functor is the right adjoint to the forgetful functor. Just like the left adjoint preserved coproducts, the right adjoint preserves products. One can therefore easily combine comonads using products (if the need arises to solve the coexpression problem).

Just like the monad is a monoid in the category of endofunctors, a comonad is a comonoid in the same category. The functor that generates a cofree comonad has the form:

type ComonadF f g = Identity :*: Compose f g

where the product of functors is defined as:

data (f :*: g) e = Both (f e) (g e)
infixr 6 :*:

Here’s the more familiar form of this functor:

data ComonadF f g e = e :< f (g e)

It is indeed a higher order functor, as witnessed by this instance:

instance Functor f => HFunctor (ComonadF f) where
  hfmap nat (e :< fge) = e :< fmap nat fge
  ffmap h (e :< fge) = h e :< fmap (fmap h) fge

A cofree comonad is the terminal coalgebra for this functor and can be written as a fixed point:

type Cofree f = FixH (ComonadF f)

Indeed, for any functor f, Cofree f is a comonad:

instance Functor f => Comonad (Cofree f) where
  extract (InH (e :< fge)) = e
  duplicate fr@(InH (e :< fge)) = 
                InH (fr :< fmap duplicate fge)

Cofree Comonad Example

The canonical example of a cofree comonad is an infinite stream:

type Stream = Cofree Identity

We can use this stream to sample a function. We’ll encapsulate this function inside the following functor (in fact, itself a comonad):

data Store a x = Store a (a -> x) 
    deriving Functor

We can use a higher order coalgebra to unpack the Store into a stream:

streamCoa :: HCoalgebra (ComonadF Identity)(Store Int)
streamCoa (Store n f) = 
    f n :< (Identity $ Store (n + 1) f)

The actual unpacking is a higher order anamorphism:

stream :: Store Int a -> Stream a
stream = hana streamCoa

We can use it, for instance, to generate a list of squares of natural numbers:

stream (Store 0 (^2))

Since, in Haskell, the same fixed point defines a terminal coalgebra as well as an initial algebra, we are free to construct algebras and catamorphisms for streams. Here’s an algebra that converts a stream to an infinite list:

listAlg :: HAlgebra (ComonadF Identity) []
listAlg(a :< Identity as) = a : as

toList :: Stream a -> [a]
toList = hcata listAlg

Future Directions

In this paper I concentrated on one type of higher order functor:

1 + a \otimes x

and its dual. This would be equivalent to studying folds for lists and unfolds for streams. But the structure of the functor category is richer than that. Just like basic data types can be combined into algebraic data types, so can functors. Moreover, besides the usual sums and products, the functor category admits at least two additional monoidal structures generated by functor composition and Day convolution.

Another potentially fruitful area of exploration is the profunctor category, which is also equipped with two monoidal structures, one defined by profunctor composition, and another by Day convolution. A free monoid with respect to profunctor composition is the basis of Haskell Arrow library [jaskelioff]. Profunctors also play an important role in the Haskell lens library [kmett].

Bibliography

  1. Erik Meijer, Maarten Fokkinga, and Ross Paterson, Functional Programming with Bananas, Lenses, Envelopes and Barbed Wire
  2. Conor McBride, Ross Paterson, Idioms: applicative programming with effects
  3. Paolo Capriotti, Ambrus Kaposi, Free Applicative Functors
  4. Wouter Swierstra, Data types a la carte
  5. Exequiel Rivas and Mauro Jaskelioff, Notions of Computation as Monoids
  6. Edward Kmett, Lenses, Folds and Traversals
  7. Richard Bird and Lambert Meertens, Nested Datatypes
  8. Patricia Johann and Neil Ghani, Initial Algebra Semantics is Enough!
 

February 20, 2018

Free Monoidal Profunctors

Posted by Bartosz Milewski under Category Theory, Haskell
[4] Comments 

Abstract: I derive free monoidal profunctors as fixed points of a higher order functor acting on profunctors. Monoidal profunctors play an important role in defining traversals.

The beauty of category theory is that it lets us reuse concepts at all levels. In my previous post I have derived a free monoidal functor that goes from a monoidal category C to Set. The current post may then be shortened to: Since profunctors are just functors from C^{op} \times C to Set, with the obvious monoidal structure induced by the tensor product in C, we automatically get free monoidal profunctors.

Let me fill in the details.

Profunctors in Haskell

Here’s the definition of a profunctor from Data.Profunctor:

class Profunctor p where
  dimap :: (s -> a) -> (b -> t) -> p a b -> p s t

The idea is that, just like a functor acts on objects, a profunctor p acts on pairs of objects \langle a, b \rangle. In other words, it’s a type constructor that takes two types as arguments. And just like a functor acts on morphisms, a profunctor acts on pairs of morphisms. The only tricky part is that the first morphism of the pair is reversed: instead of going from a to s, as one would expect, it goes from s to a. This is why we say that the first argument comes from the opposite category C^{op}, where all morphisms are reversed with respect to C. Thus a morphism from \langle a, b \rangle to \langle s, t \rangle in C^{op} \times C is a pair of morphisms \langle s \to a, b \to t \rangle.

Just like functors form a category, profunctors form a category too. In this category profunctors are objects, and natural transformations are morphisms. A natural transformation between two profunctors p and q is a family of functions which, in Haskell, can be approximated by a polymorphic function:

type p ::~> q = forall a b. p a b -> q a b

If the category C is monoidal (has a tensor product \otimes and a unit object 1), then the category C^{op} \times C has a trivially induced tensor product:

\langle a, b \rangle \otimes \langle c, d \rangle = \langle a \otimes c, b \otimes d \rangle

and unit \langle 1, 1 \rangle

In Haskell, we’ll use cartesian product (pair type) as the underlying tensor product, and () type as the unit.

Notice that the induced product does not have the usual exponential as the right adjoint. Indeed, the hom-set:

(C^{op} \times C) \, ( \langle a, b \rangle \otimes \langle c, d \rangle, \langle s, t \rangle )

is a set of pairs of morphisms:

\langle s \to a \otimes c, b \otimes d \to t \rangle

If the right adjoint existed, it would be a pair of objects \langle X, Y \rangle, such that the following hom-set would be isomorphic to the previous one:

\langle X \to a, b \to Y \rangle

While Y could be the internal hom, there is no candidate for X that would produce the isomorphism:

s \to a \otimes c \cong X \to a

(Consider, for instance, unit () for a.) This lack of the right adjoint is the reason why we can’t define an analog of Applicative for profunctors. We can, however, define a monoidal profunctor:

class Monoidal p where
  punit :: p () ()
  (>**<) :: p a b -> p c d -> p (a, c) (b, d)

This profunctor is a map between two monoidal structures. For instance, punit can be seen as mapping the unit in Set to the unit in C^{op} \times C:

punit :: () -> p <1, 1>

Operator >**< maps the product in Set to the induced product in C^{op} \times C:

(>**<) :: (p <a, b>, p <c, d>) -> p (<a, b> × <c, d>)

Day convolution, which works with monoidal structures, generalizes naturally to the profunctor category:

data PDay p q s t = forall a b c d. 
     PDay (p a b) (q c d) ((b, d) -> t) (s -> (a, c))

Higher Order Functors

Since profunctors form a category, we can define endofunctors in that category. This is a no-brainer in category theory, but it requires some new definitions in Haskell. Here’s a higher-order functor that maps a profunctor to another profunctor:

class HPFunctor pp where
  hpmap :: (p ::~> q) -> (pp p ::~> pp q)
  ddimap :: (s -> a) -> (b -> t) -> pp p a b -> pp p s t

The function hpmap lifts a natural transformation, and ddimap shows that the result of the mapping is also a profunctor.

An endofunctor in the profunctor category may have a fixed point:

newtype FixH pp a b = InH { outH :: pp (FixH pp) a b }

which is also a profunctor:

instance HPFunctor pp => Profunctor (FixH pp) where
    dimap f g (InH pp) = InH (ddimap f g pp)

Finally, our Day convolution is a higher-order endofunctor in the category of profunctors:

instance HPFunctor (PDay p) where
  hpmap nat (PDay p q from to) = PDay p (nat q) from to
  ddimap f g (PDay p q from to) = PDay p q (g . from) (to . f)

We’ll use this fact to construct a free monoidal profunctor next.

Free Monoidal Profunctor

In the previous post, I defined the free monoidal functor as a fixed point of the following endofunctor:

data FreeF f g t =
      DoneF t
    | MoreF (Day f g t)

Replacing the functors f and g with profunctors is straightforward:

data FreeP p q s t = 
      DoneP (s -> ()) (() -> t) 
    | MoreP (PDay p q s t)

The only tricky part is realizing that the first term in the sum comes from the unit of Day convolution, which is the type () -> t, and it generalizes to an appropriate pair of functions (we’ll simplify this definition later).

FreeP is a higher order endofunctor acting on profunctors:

instance HPFunctor (FreeP p) where
    hpmap _ (DoneP su ut) = DoneP su ut
    hpmap nat (MoreP day) = MoreP (hpmap nat day)
    ddimap f g (DoneP au ub) = DoneP (au . f) (g . ub)
    ddimap f g (MoreP day) = MoreP (ddimap f g day)

We can, therefore, define its fixed point:

type FreeMon p = FixH (FreeP p)

and show that it is indeed a monoidal profunctor. As before, the trick is to fist show the following property of Day convolution:

cons :: Monoidal q => PDay p q a b -> q c d -> PDay p q (a, c) (b, d)
cons (PDay pxy quv yva bxu) qcd = 
      PDay pxy (quv >**< qcd) (bimap yva id . reassoc) 
                              (assoc . bimap bxu id)

where

assoc ((a,b),c) = (a,(b,c))
reassoc (a, (b, c)) = ((a, b), c)

Using this function, we can show that FreeMon p is monoidal for any p:

instance Profunctor p => Monoidal (FreeMon p) where
  punit = InH (DoneP id id)
  (InH (DoneP au ub)) >**< frcd = dimap snd (\d -> (ub (), d)) frcd
  (InH (MoreP dayab)) >**< frcd = InH (MoreP (cons dayab frcd))

FreeMon can also be rewritten as a recursive data type:

data FreeMon p s t where
     DoneFM :: t -> FreeMon p s t
     MoreFM :: p a b -> FreeMon p c d -> 
                        (b -> d -> t) -> 
                        (s -> (a, c)) -> FreeMon p s t

Categorical Picture

As I mentioned before, from the categorical point of view there isn’t much to talk about. We define a functor in the category of profunctors:

A_p q = (C^{op} \times C) (1, -) + \int^{ a b c d } p a b \times q c d \times (C^{op} \times C) (\langle a, b \rangle \otimes \langle c, d \rangle, -)

As previously shown in the general case, its initial algebra defines a free monoidal profunctor.

Acknowledgments

I’m grateful to Eugenia Cheng not only for talking to me about monoidal profunctors, but also for getting me interested in category theory in the first place through her Catsters video series. Thanks also go to Edward Kmett for numerous discussions on this topic.

 

April 11, 2017

Profunctor Parametricity

Posted by Bartosz Milewski under Category Theory, Functional Programming, Haskell, Programming, Type System
[2] Comments 

The Free Theorem for Ends

In Haskell, the end of a profunctor p is defined as a product of all diagonal elements:

forall c. p c c

together with a family of projections:

pi :: Profunctor p => forall c. (forall a. p a a) -> p c c
pi e = e

In category theory, the end must also satisfy the edge condition which, in (type-annotated) Haskell, could be written as:

dimap f idb . pib = dimap ida f . pia

for any f :: a -> b.
Using a suitable formulation of parametricity, this equation can be shown to be a free theorem. Let’s first review the free theorem for functors before generalizing it to profunctors.

Functor Characterization

You may think of a functor as a container that has a shape and contents. You can manipulate the contents without changing the shape using fmap. In general, when applying fmap, you not only change the values stored in the container, you change their type as well. To really capture the shape of the container, you have to consider not only all possible mappings, but also more general relations between different contents.

A function is directional, and so is fmap, but relations don’t favor either side. They can map multiple values to the same value, and they can map one value to multiple values. Any relation on values induces a relation on containers. For a given functor F, if there is a relation a between type A and type A': 

A <=a=> A'

then there is a relation between type F A and F A':

F A <=(F a)=> F A'

We call this induced relation F a.

For instance, consider the relation between students and their grades. Each student may have multiple grades (if they take multiple courses) so this relation is not a function. Given a list of students and a list of grades, we would say that the lists are related if and only if they match at each position. It means that they have to be equal length, and the first grade on the list of grades must belong to the first student on the list of students, and so on. Of course, a list is a very simple container, but this property can be generalized to any functor we can define in Haskell using algebraic data types.

The fact that fmap doesn’t change the shape of the container can be expressed as a “theorem for free” using relations. We start with two related containers:

xs :: F A
xs':: F A'

where A and A' are related through some relation a. We want related containers to be fmapped to related containers. But we can’t use the same function to map both containers, because they contain different types. So we have to use two related functions instead. Related functions map related types to related types so, if we have:

f :: A -> B
f':: A'-> B'

and A is related to A' through a, we want B to be related to B' through some relation b. Also, we want the two functions to map related elements to related elements. So if x is related to x' through a, we want f x to be related to f' x' through b. In that case, we’ll say that f and f' are related through the relation that we call a->b:

f <=(a->b)=> f'

For instance, if f is mapping students’ SSNs to last names, and f' is mapping letter grades to numerical grades, the results will be related through the relation between students’ last names and their numerical grades.

To summarize, we require that for any two relations:

A <=a=> A'
B <=b=> B'

and any two functions:

f :: A -> B
f':: A'-> B'

such that:

f <=(a->b)=> f'

and any two containers:

xs :: F A
xs':: F A'

we have:

if       xs <=(F a)=> xs'
then   F xs <=(F b)=> F xs'

This characterization can be extended, with suitable changes, to contravariant functors.

Profunctor Characterization

A profunctor is a functor of two variables. It is contravariant in the first variable and covariant in the second. A profunctor can lift two functions simultaneously using dimap:

class Profunctor p where
    dimap :: (a -> b) -> (c -> d) -> p b c -> p a d

We want dimap to preserve relations between profunctor values. We start by picking any relations a, b, c, and d between types:

A <=a=> A'
B <=b=> B'
C <=c=> C'
D <=d=> D'

For any functions:

f  :: A -> B
f' :: A'-> B'
g  :: C -> D
g' :: C'-> D'

that are related through the following relations induced by function types:

f <=(a->b)=> f'
g <=(c->d)=> g'

we define:

xs :: p B C
xs':: p B'C'

The following condition must be satisfied:

if             xs <=(p b c)=> xs'
then   (p f g) xs <=(p a d)=> (p f' g') xs'

where p f g stands for the lifting of the two functions by the profunctor p.

Here’s a quick sanity check. If b and c are functions:

b :: B'-> B
c :: C -> C'

than the relation:

xs <=(p b c)=> xs'

becomes:

xs' = dimap b c xs

If a and d are functions:

a :: A'-> A
d :: D -> D'

then these relations:

f <=(a->b)=> f'
g <=(c->d)=> g'

become:

f . a = b . f'
d . g = g'. c

and this relation:

(p f g) xs <=(p a d)=> (p f' g') xs'

becomes:

(p f' g') xs' = dimap a d ((p f g) xs)

Substituting xs', we get:

dimap f' g' (dimap b c xs) = dimap a d (dimap f g xs)

and using functoriality:

dimap (b . f') (g'. c) = dimap (f . a) (d . g)

which is identically true.

Special Case of Profunctor Characterization

We are interested in the diagonal elements of a profunctor. Let’s first specialize the general case to:

C = B
C'= B'
c = b

to get:

xs = p B B
xs'= p B'B'

and

if             xs <=(p b b)=> xs'
then   (p f g) xs <=(p a d)=> (p f' g') xs'

Chosing the following substitutions:

A = A'= B
D = D'= B'
a = id
d = id
f = id
g'= id
f'= g

we get:

if              xs <=(p b b)=> xs'
then   (p id g) xs <=(p id id)=> (p g id) xs'

Since p id id is the identity relation, we get:

(p id g) xs = (p g id) xs'

or

dimap id g xs = dimap g id xs'

Free Theorem

We apply the free theorem to the term xs:

xs :: forall c. p c c

It must be related to itself through the relation that is induced by its type:

xs <=(forall b. p b b)=> xs

for any relation b:

B <=b=> B'

Universal quantification translates to a relation between different instantiations of the polymorphic value:

xsB <=(p b b)=> xsB'

Notice that we can write:

xsB = piB xs
xsB'= piB'xs

using the projections we defined earlier.

We have just shown that this equation leads to:

dimap id g xs = dimap g id xs'

which shows that the wedge condition is indeed a free theorem.

Natural Transformations

Here’s another quick application of the free theorem. The set of natural transformations may be represented as an end of the following profunctor:

type NatP a b = F a -> G b
instance Profunctor NatP where
    dimap f g alpha = fmap g . alpha . fmap f

The free theorem tells us that for any mu :: NatP c c:

(dimap id g) mu = (dimap g id) mu

which is the naturality condition:

mu . fmap g = fmap g . mu

It’s been know for some time that, in Haskell, naturality follows from parametricity, so this is not surprising.

Acknowledgment

I’d like to thank Edward Kmett for reviewing the draft of this post.

Bibliography

  1. Bartosz Milewski, Ends and Coends
  2. Edsko de Vries, Parametricity Tutorial, Part 1, Part 2, Contravariant Functions.
  3. Bartosz Milewski, Parametricity: Money for Nothing and Theorems for Free
 

February 28, 2017

F-Algebras

Posted by Bartosz Milewski under Category Theory, Haskell
[24] Comments 

This is part 24 of Categories for Programmers. Previously: Comonads. See the Table of Contents.

We’ve seen several formulations of a monoid: as a set, as a single-object category, as an object in a monoidal category. How much more juice can we squeeze out of this simple concept?

Let’s try. Take this definition of a monoid as a set m with a pair of functions:

μ :: m × m -> m
η :: 1 -> m

Here, 1 is the terminal object in Set — the singleton set. The first function defines multiplication (it takes a pair of elements and returns their product), the second selects the unit element from m. Not every choice of two functions with these signatures results in a monoid. For that we need to impose additional conditions: associativity and unit laws. But let’s forget about that for a moment and just consider “potential monoids.” A pair of functions is an element of a cartesian product of two sets of functions. We know that these sets may be represented as exponential objects:

μ ∈ m m×m
η ∈ m1

The cartesian product of these two sets is:

m m×m × m1

Using some high-school algebra (which works in every cartesian closed category), we can rewrite it as:

m m×m + 1

The plus sign stands for the coproduct in Set. We have just replaced a pair of functions with a single function — an element of the set:

m × m + 1 -> m

Any element of this set of functions is a potential monoid.

The beauty of this formulation is that it leads to interesting generalizations. For instance, how would we describe a group using this language? A group is a monoid with one additional function that assigns the inverse to every element. The latter is a function of the type m->m. As an example, integers form a group with addition as a binary operation, zero as the unit, and negation as the inverse. To define a group we would start with a triple of functions:

m × m -> m
m -> m
1 -> m

As before, we can combine all these triples into one set of functions:

m × m + m + 1 -> m

We started with one binary operator (addition), one unary operator (negation), and one nullary operator (identity — here zero). We combined them into one function. All functions with this signature define potential groups.

We can go on like this. For instance, to define a ring, we would add one more binary operator and one nullary operator, and so on. Each time we end up with a function type whose left-hand side is a sum of powers (possibly including the zeroth power — the terminal object), and the right-hand side being the set itself.

Now we can go crazy with generalizations. First of all, we can replace sets with objects and functions with morphisms. We can define n-ary operators as morphisms from n-ary products. It means that we need a category that supports finite products. For nullary operators we require the existence of the terminal object. So we need a cartesian category. In order to combine these operators we need exponentials, so that’s a cartesian closed category. Finally, we need coproducts to complete our algebraic shenanigans.

Alternatively, we can just forget about the way we derived our formulas and concentrate on the final product. The sum of products on the left hand side of our morphism defines an endofunctor. What if we pick an arbitrary endofunctor F instead? In that case we don’t have to impose any constraints on our category. What we obtain is called an F-algebra.

An F-algebra is a triple consisting of an endofunctor F, an object a, and a morphism

F a -> a

The object is often called the carrier, an underlying object or, in the context of programming, the carrier type. The morphism is often called the evaluation function or the structure map. Think of the functor F as forming expressions and the morphism as evaluating them.

Here’s the Haskell definition of an F-algebra:

type Algebra f a = f a -> a

It identifies the algebra with its evaluation function.

In the monoid example, the functor in question is:

data MonF a = MEmpty | MAppend a a

This is Haskell for 1 + a × a (remember algebraic data structures).

A ring would be defined using the following functor:

data RingF a = RZero
             | ROne
             | RAdd a a 
             | RMul a a
             | RNeg a

which is Haskell for 1 + 1 + a × a + a × a + a.

An example of a ring is the set of integers. We can choose Integer as the carrier type and define the evaluation function as:

evalZ :: Algebra RingF Integer
evalZ RZero      = 0
evalZ ROne       = 1
evalZ (RAdd m n) = m + n
evalZ (RMul m n) = m * n
evalZ (RNeg n)   = -n

There are more F-algebras based on the same functor RingF. For instance, polynomials form a ring and so do square matrices.

As you can see, the role of the functor is to generate expressions that can be evaluated using the evaluator of the algebra. So far we’ve only seen very simple expressions. We are often interested in more elaborate expressions that can be defined using recursion.

Recursion

One way to generate arbitrary expression trees is to replace the variable a inside the functor definition with recursion. For instance, an arbitrary expression in a ring is generated by this tree-like data structure:

data Expr = RZero
          | ROne
          | RAdd Expr Expr 
          | RMul Expr Expr
          | RNeg Expr

We can replace the original ring evaluator with its recursive version:

evalZ :: Expr -> Integer
evalZ RZero        = 0
evalZ ROne         = 1
evalZ (RAdd e1 e2) = evalZ e1 + evalZ e2
evalZ (RMul e1 e2) = evalZ e1 * evalZ e2
evalZ (RNeg e)     = -(evalZ e)

This is still not very practical, since we are forced to represent all integers as sums of ones, but it will do in a pinch.

But how can we describe expression trees using the language of F-algebras? We have to somehow formalize the process of replacing the free type variable in the definition of our functor, recursively, with the result of the replacement. Imagine doing this in steps. First, define a depth-one tree as:

type RingF1 a = RingF (RingF a)

We are filling the holes in the definition of RingF with depth-zero trees generated by RingF a. Depth-2 trees are similarly obtained as:

type RingF2 a = RingF (RingF (RingF a))

which we can also write as:

type RingF2 a = RingF (RingF1 a)

Continuing this process, we can write a symbolic equation:

type RingFn+1 a = RingF (RingFn a)

Conceptually, after repeating this process infinitely many times, we end up with our Expr. Notice that Expr does not depend on a. The starting point of our journey doesn’t matter, we always end up in the same place. This is not always true for an arbitrary endofunctor in an arbitrary category, but in the category Set things are nice.

Of course, this is a hand-waving argument, and I’ll make it more rigorous later.

Applying an endofunctor infinitely many times produces a fixed point, an object defined as:

Fix f = f (Fix f)

The intuition behind this definition is that, since we applied f infinitely many times to get Fix f, applying it one more time doesn’t change anything. In Haskell, the definition of a fixed point is:

newtype Fix f = Fix (f (Fix f))

Arguably, this would be more readable if the constructor’s name were different than the name of the type being defined, as in:

newtype Fix f = In (f (Fix f))

but I’ll stick with the accepted notation. The constructor Fix (or In, if you prefer) can be seen as a function:

Fix :: f (Fix f) -> Fix f

There is also a function that peels off one level of functor application:

unFix :: Fix f -> f (Fix f)
unFix (Fix x) = x

The two functions are the inverse of each other. We’ll use these functions later.

Category of F-Algebras

Here’s the oldest trick in the book: Whenever you come up with a way of constructing some new objects, see if they form a category. Not surprisingly, algebras over a given endofunctor F form a category. Objects in that category are algebras — pairs consisting of a carrier object a and a morphism F a -> a, both from the original category C.

To complete the picture, we have to define morphisms in the category of F-algebras. A morphism must map one algebra (a, f) to another algebra (b, g). We’ll define it as a morphism m that maps the carriers — it goes from a to b in the original category. Not any morphism will do: we want it to be compatible with the two evaluators. (We call such a structure-preserving morphism a homomorphism.) Here’s how you define a homomorphism of F-algebras. First, notice that we can lift m to the mapping:

F m :: F a -> F b

we can then follow it with g to get to b. Equivalently, we can use f to go from F a to a and then follow it with m. We want the two paths to be equal:

g ∘ F m = m ∘ f

alg

It’s easy to convince yourself that this is indeed a category (hint: identity morphisms from C work just fine, and a composition of homomorphisms is a homomorphism).

An initial object in the category of F-algebras, if it exists, is called the initial algebra. Let’s call the carrier of this initial algebra i and its evaluator j :: F i -> i. It turns out that j, the evaluator of the initial algebra, is an isomorphism. This result is known as Lambek’s theorem. The proof relies on the definition of the initial object, which requires that there be a unique homomorphism m from it to any other F-algebra. Since m is a homomorphism, the following diagram must commute:

alg2

Now let’s construct an algebra whose carrier is F i. The evaluator of such an algebra must be a morphism from F (F i) to F i. We can easily construct such an evaluator simply by lifting j:

F j :: F (F i) -> F i

Because (i, j) is the initial algebra, there must be a unique homomorphism m from it to (F i, F j). The following diagram must commute:

alg3a

But we also have this trivially commuting diagram (both paths are the same!):

alg3

which can be interpreted as showing that j is a homomorphism of algebras, mapping (F i, F j) to (i, j). We can glue these two diagrams together to get:

alg4

This diagram may, in turn, be interpreted as showing that j ∘ m is a homomorphism of algebras. Only in this case the two algebras are the same. Moreover, because (i, j) is initial, there can only be one homomorphism from it to itself, and that’s the identity morphism idi — which we know is a homomorphism of algebras. Therefore j ∘ m = idi. Using this fact and the commuting property of the left diagram we can prove that m ∘ j = idFi. This shows that m is the inverse of j and therefore j is an isomorphism between F i and i:

F i ≅ i

But that is just saying that i is a fixed point of F. That’s the formal proof behind the original hand-waving argument.

Back to Haskell: We recognize i as our Fix f, j as our constructor Fix, and its inverse as unFix. The isomorphism in Lambek’s theorem tells us that, in order to get the initial algebra, we take the functor f and replace its argument a with Fix f. We also see why the fixed point does not depend on a.

Natural Numbers

Natural numbers can also be defined as an F-algebra. The starting point is the pair of morphisms:

zero :: 1 -> N
succ :: N -> N

The first one picks the zero, and the second one maps all numbers to their successors. As before, we can combine the two into one:

1 + N -> N

The left hand side defines a functor which, in Haskell, can be written like this:

data NatF a = ZeroF | SuccF a

The fixed point of this functor (the initial algebra that it generates) can be encoded in Haskell as:

data Nat = Zero | Succ Nat

A natural number is either zero or a successor of another number. This is known as the Peano representation for natural numbers.

Catamorphisms

Let’s rewrite the initiality condition using Haskell notation. We call the initial algebra Fix f. Its evaluator is the contructor Fix. There is a unique morphism m from the initial algebra to any other algebra over the same functor. Let’s pick an algebra whose carrier is a and the evaluator is alg.

alg5
By the way, notice what m is: It’s an evaluator for the fixed point, an evaluator for the whole recursive expression tree. Let’s find a general way of implementing it.

Lambek’s theorem tells us that the constructor Fix is an isomorphism. We called its inverse unFix. We can therefore flip one arrow in this diagram to get:

alg6

Let’s write down the commutation condition for this diagram:

m = alg . fmap m . unFix

We can interpret this equation as a recursive definition of m. The recursion is bound to terminate for any finite tree created using the functor f. We can see that by noticing that fmap m operates underneath the top layer of the functor f. In other words, it works on the children of the original tree. The children are always one level shallower than the original tree.

Here’s what happens when we apply m to a tree constructed using Fix f. The action of unFix peels off the constructor, exposing the top level of the tree. We then apply m to all the children of the top node. This produces results of type a. Finally, we combine those results by applying the non-recursive evaluator alg. The key point is that our evaluator alg is a simple non-recursive function.

Since we can do this for any algebra alg, it makes sense to define a higher order function that takes the algebra as a parameter and gives us the function we called m. This higher order function is called a catamorphism:

cata :: Functor f => (f a -> a) -> Fix f -> a
cata alg = alg . fmap (cata alg) . unFix

Let’s see an example of that. Take the functor that defines natural numbers:

data NatF a = ZeroF | SuccF a

Let’s pick (Int, Int) as the carrier type and define our algebra as:

fib :: NatF (Int, Int) -> (Int, Int)
fib ZeroF = (1, 1)
fib (SuccF (m, n)) = (n, m + n)

You can easily convince yourself that the catamorphism for this algebra, cata fib, calculates Fibonacci numbers.

In general, an algebra for NatF defines a recurrence relation: the value of the current element in terms of the previous element. A catamorphism then evaluates the n-th element of that sequence.

Folds

A list of e is the initial algebra of the following functor:

data ListF e a = NilF | ConsF e a

Indeed, replacing the variable a with the result of recursion, which we’ll call List e, we get:

data List e = Nil | Cons e (List e)

An algebra for a list functor picks a particular carrier type and defines a function that does pattern matching on the two constructors. Its value for NilF tells us how to evaluate an empty list, and its value for ConsF tells us how to combine the current element with the previously accumulated value.

For instance, here’s an algebra that can be used to calculate the length of a list (the carrier type is Int):

lenAlg :: ListF e Int -> Int
lenAlg (ConsF e n) = n + 1
lenAlg NilF = 0

Indeed, the resulting catamorphism cata lenAlg calculates the length of a list. Notice that the evaluator is a combination of (1) a function that takes a list element and an accumulator and returns a new accumulator, and (2) a starting value, here zero. The type of the value and the type of the accumulator are given by the carrier type.

Compare this to the traditional Haskell definition:

length = foldr (\e n -> n + 1) 0

The two arguments to foldr are exactly the two components of the algebra.

Let’s try another example:

sumAlg :: ListF Double Double -> Double
sumAlg (ConsF e s) = e + s
sumAlg NilF = 0.0

Again, compare this with:

sum = foldr (\e s -> e + s) 0.0

As you can see, foldr is just a convenient specialization of a catamorphism to lists.

Coalgebras

As usual, we have a dual construction of an F-coagebra, where the direction of the morphism is reversed:

a -> F a

Coalgebras for a given functor also form a category, with homomorphisms preserving the coalgebraic structure. The terminal object (t, u) in that category is called the terminal (or final) coalgebra. For every other algebra (a, f) there is a unique homomorphism m that makes the following diagram commute:

alg7

A terminal colagebra is a fixed point of the functor, in the sense that the morphism u :: t -> F t is an isomorphism (Lambek’s theorem for coalgebras):

F t ≅ t

A terminal coalgebra is usually interpreted in programming as a recipe for generating (possibly infinite) data structures or transition systems.

Just like a catamorphism can be used to evaluate an initial algebra, an anamorphism can be used to coevaluate a terminal coalgebra:

ana :: Functor f => (a -> f a) -> a -> Fix f
ana coalg = Fix . fmap (ana coalg) . coalg

A canonical example of a coalgebra is based on a functor whose fixed point is an infinite stream of elements of type e. This is the functor:

data StreamF e a = StreamF e a
  deriving Functor

and this is its fixed point:

data Stream e = Stream e (Stream e)

A coalgebra for StreamF e is a function that takes the seed of type a and produces a pair (StreamF is a fancy name for a pair) consisting of an element and the next seed.

You can easily generate simple examples of coalgebras that produce infinite sequences, like the list of squares, or reciprocals.

A more interesting example is a coalgebra that produces a list of primes. The trick is to use an infinite list as a carrier. Our starting seed will be the list [2..]. The next seed will be the tail of this list with all multiples of 2 removed. It’s a list of odd numbers starting with 3. In the next step, we’ll take the tail of this list and remove all multiples of 3, and so on. You might recognize the makings of the sieve of Eratosthenes. This coalgebra is implemented by the following function:

era :: [Int] -> StreamF Int [Int]
era (p : ns) = StreamF p (filter (notdiv p) ns)
    where notdiv p n = n `mod` p /= 0

The anamorphism for this coalgebra generates the list of primes:

primes = ana era [2..]

A stream is an infinite list, so it should be possible to convert it to a Haskell list. To do that, we can use the same functor StreamF to form an algebra, and we can run a catamorphism over it. For instance, this is a catamorphism that converts a stream to a list:

toListC :: Fix (StreamF e) -> [e]
toListC = cata al
   where al :: StreamF e [e] -> [e]
         al (StreamF e a) = e : a

Here, the same fixed point is simultaneously an initial algebra and a terminal coalgebra for the same endofunctor. It’s not always like this, in an arbitrary category. In general, an endofunctor may have many (or no) fixed points. The initial algebra is the so called least fixed point, and the terminal coalgebra is the greatest fixed point. In Haskell, though, both are defined by the same formula, and they coincide.

The anamorphism for lists is called unfold. To create finite lists, the functor is modified to produce a Maybe pair:

unfoldr :: (b -> Maybe (a, b)) -> b -> [a]

The value of Nothing will terminate the generation of the list.

An interesting case of a coalgebra is related to lenses. A lens can be represented as a pair of a getter and a setter:

set :: a -> s -> a
get :: a -> s

Here, a is usually some product data type with a field of type s. The getter retrieves the value of that field and the setter replaces this field with a new value. These two functions can be combined into one:

a -> (s, s -> a)

We can rewrite this function further as:

a -> Store s a

where we have defined a functor:

data Store s a = Store (s -> a) s

Notice that this is not a simple algebraic functor constructed from sums of products. It involves an exponential as.

A lens is a coalgebra for this functor with the carrier type a. We’ve seen before that Store s is also a comonad. It turns out that a well-behaved lens corresponds to a coalgebra that is compatible with the comonad structure. We’ll talk about this in the next section.

Challenges

  1. Implement the evaluation function for a ring of polynomials of one variable. You can represent a polynomial as a list of coefficients in front of powers of x. For instance, 4x2-1 would be represented as (starting with the zero’th power) [-1, 0, 4].
  2. Generalize the previous construction to polynomials of many independent variables, like x2y-3y3z.
  3. Implement the algebra for the ring of 2×2 matrices.
  4. Define a coalgebra whose anamorphism produces a list of squares of natural numbers.
  5. Use unfoldr to generate a list of the first n primes.

Next: Algebras for Monads.

 

February 6, 2017

Applicative Functors

Posted by Bartosz Milewski under Category Theory, Functional Programming, Haskell, Type System
[5] Comments 

Unlike monads, which came into programming straight from category theory, applicative functors have their origins in programming. McBride and Paterson introduced applicative functors as a programming pearl in their paper Applicative programming with effects. They also provided a categorical interpretation of applicatives in terms of strong lax monoidal functors. It’s been accepted that, just like “a monad is a monoid in the category of endofunctors,” so “an applicative is a strong lax monoidal functor.”

The so called “tensorial strength” seems to be important in categorical semantics, and in his seminal paper Notions of computation and monads, Moggi argued that effects should be described using strong monads. It makes sense, considering that a computation is done in a context, and you should be able to make the global context available under the monad. The fact that we don’t talk much about strong monads in Haskell is due to the fact that all functors in the category Set, which underlies the Haskell’s type system, have canonical strength. So why do we talk about strength when dealing with applicative functors? I have looked into this question and came to the conclusion that there is no fundamental reason, and that it’s okay to just say:

An applicative is a lax monoidal functor

In this post I’ll discuss different equivalent categorical definitions of the applicative functor. I’ll start with a lax closed functor, then move to a lax monoidal functor, and show the equivalence of the two definitions. Then I’ll introduce the calculus of ends and show that the third definition of the applicative functor as a monoid in a suitable functor category equipped with Day convolution is equivalent to the previous ones.

Applicative as a Lax Closed Functor

The standard definition of the applicative functor in Haskell reads:

class Functor f => Applicative f where
    (<*>) :: f (a -> b) -> (f a -> f b)
    pure :: a -> f a

At first sight it doesn’t seem to involve a monoidal structure. It looks more like preserving function arrows (I added some redundant parentheses to suggest this interpretation).

Categorically, functors that “preserve arrows” are known as closed functors. Let’s look at a definition of a closed functor f between two categories C and D. We have to assume that both categories are closed, meaning that they have internal hom-objects for every pair of objects. Internal hom-objects are also called function objects or exponentials. They are normally defined through the right adjoint to the product functor:

C(z × a, b) ≅ C(z, a => b)

To distinguish between sets of morphisms and function objects (they are the same thing in Set), I will temporarily use double arrows for function objects.

We can take a functor f and act with it on the function object a=>b in the category C. We get an object f (a=>b) in D. Or we can map the two objects a and b from C to D and then construct the function object in D: f a => f b.

closed

We call a functor closed if the two results are isomorphic (I have subscripted the two arrows with the categories where they are defined):

f (a =>C b) ≅ (f a =>D f b)

and if the functor preserves the unit object:

iD ≅ f iC

What’s the unit object? Normally, this is the unit with respect to the same product that was used to define the function object using the adjunction. I’m saying “normally,” because it’s possible to define a closed category without a product.

Note: The two arrows and the two is are defined with respect to two different products. The first isomorphism must be natural in both a and b. Also, to complete the picture, there are some diagrams that must commute.

The two isomorphisms that define a closed functor can be relaxed and replaced by unidirectional morphisms. The result is a lax closed functor:

f (a => b) -> (f a => f b)
i -> f i

This looks almost like the definition of Applicative, except for one problem: how can we recover the natural transformation we call pure from a single morphism i -> f i.

One way to do it is from the position of strength. An endofunctor f has tensorial strength if there is a natural transformation:

stc a :: c ⊗ f a -> f (c ⊗ a)

Think of c as the context in which the computation f a is performed. Strength means that we can use this external context inside the computation.

In the category Set, with the tensor product replaced by cartesian product, all functors have canonical strength. In Haskell, we would define it as:

st (c, fa) = fmap ((,) c) fa

The morphism in the definition of the lax closed functor translates to:

unit :: () -> f ()

Notice that, up to isomorphism, the unit type () is the unit with respect to cartesian product. The relevant isomorphisms are:

λa :: ((), a) -> a
ρa :: (a, ()) -> a

Here’s the derivation from Rivas and Jaskelioff’s Notions of Computation as Monoids:

    a
≅  (a, ())   -- unit law, ρ-1
-> (a, f ()) -- lax unit
-> f (a, ()) -- strength
≅  f a       -- lifted unit law, f ρ

Strength is necessary if you’re starting with a lax closed (or monoidal — see the next section) endofunctor in an arbitrary closed (or monoidal) category and you want to derive pure within that category — not after you restrict it to Set.

There is, however, an alternative derivation using the Yoneda lemma:

f ()
≅ forall a. (() -> a) -> f a  -- Yoneda
≅ forall a. a -> f a -- because: (() -> a) ≅ a

We recover the whole natural transformation from a single value. The advantage of this derivation is that it generalizes beyond endofunctors and it doesn’t require strength. As we’ll see later, it also ties nicely with the Day-convolution definition of applicative. The Yoneda lemma only works for Set-valued functors, but so does Day convolution (there are enriched versions of both Yoneda and Day convolution, but I’m not going to discuss them here).

We can define the categorical version of the Haskell’s applicative functor as a lax closed functor going from a closed category C to Set. It’s a functor equipped with a natural transformation:

f (a => b) -> (f a -> f b)

where a=>b is the internal hom-object in C (the second arrow is a function type in Set), and a function:

1 -> f i

where 1 is the singleton set and i is the unit object in C.

The importance of a categorical definition is that it comes with additional identities or “axioms.” A lax closed functor must be compatible with the structure of both categories. I will not go into details here, because we are really only interested in closed categories that are monoidal, where these axioms are easier to express.

The definition of a lax closed functor is easily translated to Haskell:

class Functor f => Closed f where
    (<*>) :: f (a -> b) -> f a -> f b
    unit :: f ()

Applicative as a Lax Monoidal Functor

Even though it’s possible to define a closed category without a monoidal structure, in practice we usually work with monoidal categories. This is reflected in the equivalent definition of the Haskell’s applicative functor as a lax monoidal functor. In Haskell, we would write:

class Functor f => Monoidal f where
    (>*<) :: (f a, f b) -> f (a, b)
    unit :: f ()

This definition is equivalent to our previous definition of a closed functor. That’s because, as we’ve seen, a function object in a monoidal category is defined in terms of a product. We can show the equivalence in a more general categorical setting.

This time let’s start with a symmetric closed monoidal category C, in which the function object is defined through the right adjoint to the tensor product:

C(z ⊗ a, b) ≅ C(z, a => b)

As usual, the tensor product is associative and unital — with the unit object i — up to isomorphism. The symmetry is defined through natural isomorphism:

γ :: a ⊗ b -> b ⊗ a

A functor f between two monoidal categories is lax monoidal if there exist: (1) a natural transformation

f a ⊗ f b -> f (a ⊗ b)

and (2) a morphism

i -> f i

Notice that the products and units on either side of the two mappings are from different categories.

A (lax-) monoidal functor must also preserve associativity and unit laws.

For instance a triple product

f a ⊗ (f b ⊗ f c)

may be rearranged using an associator α to give

(f a ⊗ f b) ⊗ f c

then converted to

f (a ⊗ b) ⊗ f c

and then to

f ((a ⊗ b) ⊗ c)

Or it could be first converted to

f a ⊗ f (b ⊗ c)

and then to

f (a ⊗ (b ⊗ c))

These two should be equivalent under the associator in C.

assoc

Similarly, f a ⊗ i can be simplified to f a using the right unitor ρ in D. Or it could be first converted to f a ⊗ f i, then to f (a ⊗ i), and then to f a, using the right unitor in C. The two paths should be equivalent. (Similarly for the left identity.)

unit

We will now consider functors from C to Set, with Set equipped with the usual cartesian product, and the singleton set as unit. A lax monoidal functor is defined by: (1) a natural transformation:

(f a, f b) -> f (a ⊗ b)

and (2) a choice of an element of the set f i (a function from 1 to f i picks an element from that set).

We need the target category to be Set because we want to be able to use the Yoneda lemma to show equivalence with the standard definition of applicative. I’ll come back to this point later.

The Equivalence

The definitions of a lax closed and a lax monoidal functors are equivalent when C is a closed symmetric monoidal category. The proof relies on the existence of the adjunction, in particular the unit and the counit of the adjunction:

ηa :: a -> (b => (a ⊗ b))
εb :: (a => b) ⊗ a -> b

For instance, let’s assume that f is lax-closed. We want to construct the mapping

(f a, f b) -> f (a ⊗ b)

First, we apply the lifted pair (unit, identity), (f η, f id)

(f a -> f (b => a ⊗ b), f id)

to the left hand side. We get:

(f (b => a ⊗ b), f b)

Now we can use (the uncurried version of) the lax-closed morphism:

(f (b => x), f b) -> f x

to get:

f (a ⊗ b)

Conversely, assuming the lax-monoidal property we can show that the functor is lax-closed, that is to say, implement the following function:

(f (a => b), f a) -> f b

First we use the lax monoidal morphism on the left hand side:

f ((a => b) ⊗ a)

and then use the counit (a.k.a. the evaluation morphism) to get the desired result f b

There is yet another presentation of applicatives using Day convolution. But before we get there, we need a little refresher on calculus.

Calculus of Ends

Ends and coends are very useful constructs generalizing limits and colimits. They are defined through universal constructions. They have a few fundamental properties that are used over and over in categorical calculations. I’ll just introduce the notation and a few important identities. We’ll be working in a symmetric monoidal category C with functors from C to Set and profunctors from Cop×C to Set. The end of a profunctor p is a set denoted by:

∫a p a a

The most important thing about ends is that a set of natural transformations between two functors f and g can be represented as an end:

[C, Set](f, g) = ∫a C(f a, g a)

In Haskell, the end corresponds to universal quantification over a functor of mixed variance. For instance, the natural transformation formula takes the familiar form:

forall a. f a -> g a

The Yoneda lemma, which deals with natural transformations, can also be written using an end:

∫z (C(a, z) -> f z) ≅ f a

In Haskell, we can write it as the equivalence:

forall z. ((a -> z) -> f z) ≅ f a

which is a generalization of the continuation passing transform.

The dual notion of coend is similarly written using an integral sign, with the “integration variable” in the superscript position:

∫ a p a a

In pseudo-Haskell, a coend is represented by an existential quantifier. It’s possible to define existential data types in Haskell by converting existential quantification to universal one. The relevant identity in terms of coends and ends reads:

(∫ z p z z) -> y ≅ ∫ z (p z z -> y)

In Haskell, this formula is used to turn functions that take existential types to functions that are polymorphic:

(exists z. p z z) -> y ≅ forall z. (p z z -> y)

Intuitively, it makes perfect sense. If you want to define a function that takes an existential type, you have to be prepared to handle any type.

The equivalent of the Yoneda lemma for coends reads:

∫ z f z × C(z, a) ≅ f a

or, in pseudo-Haskell:

exists z. (f z, z -> a) ≅ f a

(The intuition is that the only thing you can do with this pair is to fmap the function over the first component.)

There is also a contravariant version of this identity:

∫ z C(a, z) × f z ≅ f a

where f is a contravariant functor (a.k.a., a presheaf). In pseudo-Haskell:

exists z. (a -> z, f z) ≅ f a

(The intuition is that the only thing you can do with this pair is to apply the contramap of the first component to the second component.)

Using coends we can define a tensor product in the category of functors [C, Set]. This product is called Day convolution:

(f ★ g) a = ∫ x y f x × g y × C(x ⊗ y, a)

It is a bifunctor in that category (read, it can be used to lift natural transformations). It’s associative and symmetric up to isomorphism. It also has a unit — the hom-functor C(i, -), where i is the monoidal unit in C. In other words, Day convolution imbues the category [C, Set] with monoidal structure.

Let’s verify the unit laws.

(C(i, -) ★ g) a = ∫ x y C(i, x) × g y × C(x ⊗ y, a)

We can use the contravariant Yoneda to “integrate over x” to get:

∫ y g y × C(i ⊗ y, a)

Considering that i is the unit of the tensor product in C, we get:

∫ y g y × C(y, a)

Covariant Yoneda lets us “integrate over y” to get the desired g a. The same method works for the right unit law.

Applicative as a Monoid

Given a monoidal category, we can always define a monoid as an object m equipped with two morphisms:

μ :: m ⊗ m -> m
η :: i -> m

satisfying the laws of associativity and unitality.

We have shown that the functor category [C, Set] (with C a symmetric monoidal category) is monoidal under Day convolution. An object in this category is a functor f. The two morphisms that would make it a candidate for a monoid are natural transformations:

μ :: f ★ f -> f
η :: C(i, -) -> f

The a component of the natural transformation μ can be rewritten as:

(∫ x y f x × f y × C(x ⊗ y, a)) -> f a

which is equivalent to:

∫x y (f x × f y × C(x ⊗ y, a) -> f a)

or, upon currying:

∫x y (f x, f y) -> C(x ⊗ y, a) -> f a

It turns out that so defined monoid is equivalent to a lax monoidal functor. This was shown by Rivas and Jaskelioff. The following derivation is due to Bob Atkey.

The trick is to start with the whole set of natural transformation from f★f to f. The multiplication μ is just one of them. We’ll express the set of natural transformations as an end:

∫ a ((f ★ f) a -> f a)

Plugging in the formula for the a component of μ, we get:

∫ a x y (f x, f y) -> C(x ⊗ y, a) -> f a

The end over a does not involve the first argument, so we can move the integral sign:

∫ x y (f x, f y) -> ∫ a C(x ⊗ y, a) -> f a

Then we use the Yoneda lemma to “perform the integration” over a:

∫ x y (f x, f y) -> f (x ⊗ y)

You may recognize this as a set of natural transformations that define a lax monoidal functor. We have established a one-to-one correspondence between these natural transformations and the ones defining monoidal multiplication using Day convolution.

The remaining part is to show the equivalence between the unit with respect to Day convolution and the second part of the definition of the lax monoidal functor, the morphism:

1 -> f i

We start with the set of natural transformations that contains our η:

∫ a (i -> a) -> f a

By Yoneda, this is just f i. Picking an element from a set is equivalent to defining a morphism from the singleton set 1, so for any choice of η we get:

1 -> f i

and vice versa. The two definitions are equivalent.

Notice that the monoidal unit η under Day convolution becomes the definition of pure in the Haskell version of applicative. Indeed, when we replace the category C with Set, f becomes and endofunctor, and the unit of Day convolution C(i, -) becomes the identity functor Id. We get:

η :: Id -> f

or, in components:

pure :: a -> f a

So, strictly speaking, the Haskell definition of Applicative mixes the elements of the lax closed functor and the monoidal unit under Day convolution.

Acknowledgments

I’m grateful to Mauro Jaskelioff and Exequiel Rivas for correspondence and to Bob Atkey, Dimitri Chikhladze, and Make Shulman for answering my questions on Math Overflow.

 

Next Page »