Bartosz Milewski's Programming Cafe

This is part 8 of Categories for Programmers. Previously: Functors. See the Table of Contents.

Now that you know what a functor is, and have seen a few examples, let’s see how we can build larger functors from smaller ones. In particular it’s interesting to see which type constructors (which correspond to mappings between objects in a category) can be extended to functors (which include mappings between morphisms).

Bifunctors

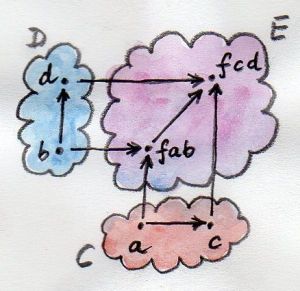
Since functors are morphisms in Cat (the category of categories), a lot of intuitions about morphisms — and functions in particular — apply to functors as well. For instance, just like you can have a function of two arguments, you can have a functor of two arguments, or a bifunctor. On objects, a bifunctor maps every pair of objects, one from category C, and one from category D, to an object in category E. Notice that this is just saying that it’s a mapping from a cartesian product of categories C×D to E.

That’s pretty straightforward. But functoriality means that a bifunctor has to map morphisms as well. This time, though, it must map a pair of morphisms, one from C and one from D, to a morphism in E.

Again, a pair of morphisms is just a single morphism in the product category C×D. We define a morphism in a cartesian product of categories as a pair of morphisms which goes from one pair of objects to another pair of objects. These pairs of morphisms can be composed in the obvious way:

(f, g) ∘ (f', g') = (f ∘ f', g ∘ g')

The composition is associative and it has an identity — a pair of identity morphisms (id, id). So a cartesian product of categories is indeed a category.

An easier way to think about bifunctors would be to consider them functors in each argument separately. So instead of translating functorial laws — associativity and identity preservation — from functors to bifunctors, it would be enough to check them separately for each argument. However, in general, separate functoriality is not enough to prove joint functoriality. Categories in which joint functoriality fails are called premonoidal.

Let’s define a bifunctor in Haskell. In this case all three categories are the same: the category of Haskell types. A bifunctor is a type constructor that takes two type arguments. Here’s the definition of the Bifunctor typeclass taken directly from the library Control.Bifunctor:

class Bifunctor f where
    bimap :: (a -> c) -> (b -> d) -> f a b -> f c d
    bimap g h = first g . second h
    first :: (a -> c) -> f a b -> f c b
    first g = bimap g id
    second :: (b -> d) -> f a b -> f a d
    second = bimap id

The type variable f represents the bifunctor. You can see that in all type signatures it’s always applied to two type arguments. The first type signature defines bimap: a mapping of two functions at once. The result is a lifted function, (f a b -> f c d), operating on types generated by the bifunctor’s type constructor. There is a default implementation of bimap in terms of first and second, which shows that it’s enough to have functoriality in each argument separately to be able to define a bifunctor. (As mentioned before, this doesn’t always work, because the two maps may not commute, that is first g . second h may not be the same as second h . first g.)

The two other type signatures, first and second, are the two fmaps witnessing the functoriality of f in the first and the second argument, respectively.

first

second

The typeclass definition provides default implementations for both of them in terms of bimap.

When declaring an instance of Bifunctor, you have a choice of either implementing bimap and accepting the defaults for first and second, or implementing both first and second and accepting the default for bimap (of course, you may implement all three of them, but then it’s up to you to make sure they are related to each other in this manner).

Product and Coproduct Bifunctors

An important example of a bifunctor is the categorical product — a product of two objects that is defined by a universal construction. If the product exists for any pair of objects, the mapping from those objects to the product is bifunctorial. This is true in general, and in Haskell in particular. Here’s the Bifunctor instance for a pair constructor — the simplest product type:

instance Bifunctor (,) where
    bimap f g (x, y) = (f x, g y)

There isn’t much choice: bimap simply applies the first function to the first component, and the second function to the second component of a pair. The code pretty much writes itself, given the types:

bimap :: (a -> c) -> (b -> d) -> (a, b) -> (c, d)

The action of the bifunctor here is to make pairs of types, for instance:

(,) a b = (a, b)

By duality, a coproduct, if it’s defined for every pair of objects in a category, is also a bifunctor. In Haskell, this is exemplified by the Either type constructor being an instance of Bifunctor:

instance Bifunctor Either where
    bimap f _ (Left x)  = Left (f x)
    bimap _ g (Right y) = Right (g y)

This code also writes itself.

Now, remember when we talked about monoidal categories? A monoidal category defines a binary operator acting on objects, together with a unit object. I mentioned that Set is a monoidal category with respect to cartesian product, with the singleton set as a unit. And it’s also a monoidal category with respect to disjoint union, with the empty set as a unit. What I haven’t mentioned is that one of the requirements for a monoidal category is that the binary operator be a bifunctor. This is a very important requirement — we want the monoidal product to be compatible with the structure of the category, which is defined by morphisms. We are now one step closer to the full definition of a monoidal category (we still need to learn about naturality, before we can get there).

Functorial Algebraic Data Types

We’ve seen several examples of parameterized data types that turned out to be functors — we were able to define fmap for them. Complex data types are constructed from simpler data types. In particular, algebraic data types (ADTs) are created using sums and products. We have just seen that sums and products are functorial. We also know that functors compose. So if we can show that the basic building blocks of ADTs are functorial, we’ll know that parameterized ADTs are functorial too.

So what are the building blocks of parameterized algebraic data types? First, there are the items that have no dependency on the type parameter of the functor, like Nothing in Maybe, or Nil in List. They are equivalent to the Const functor. Remember, the Const functor ignores its type parameter (really, the second type parameter, which is the one of interest to us, the first one being kept constant).

Then there are the elements that simply encapsulate the type parameter itself, like Just in Maybe. They are equivalent to the identity functor. I mentioned the identity functor previously, as the identity morphism in Cat, but didn’t give its definition in Haskell. Here it is:

data Identity a = Identity a

instance Functor Identity where
    fmap f (Identity x) = Identity (f x)

You can think of Identity as the simplest possible container that always stores just one (immutable) value of type a.

Everything else in algebraic data structures is constructed from these two primitives using products and sums.

With this new knowledge, let’s have a fresh look at the Maybe type constructor:

data Maybe a = Nothing | Just a

It’s a sum of two types, and we now know that the sum is functorial. The first part, Nothing can be represented as a Const () acting on a (the first type parameter of Const is set to unit — later we’ll see more interesting uses of Const). The second part is just a different name for the identity functor. We could have defined Maybe, up to isomorphism, as:

type Maybe a = Either (Const () a) (Identity a)

So Maybe is the composition of the bifunctor Either with two functors, Const () and Identity. (Const is really a bifunctor, but here we always use it partially applied.)

We’ve already seen that a composition of functors is a functor — we can easily convince ourselves that the same is true of bifunctors. All we need is to figure out how a composition of a bifunctor with two functors works on morphisms. Given two morphisms, we simply lift one with one functor and the other with the other functor. We then lift the resulting pair of lifted morphisms with the bifunctor.

We can express this composition in Haskell. Let’s define a data type that is parameterized by a bifunctor bf (it’s a type variable that is a type constructor that takes two types as arguments), two functors fu and gu (type constructors that take one type variable each), and two regular types a and b. We apply fu to a and gu to b, and then apply bf to the resulting two types:

newtype BiComp bf fu gu a b = BiComp (bf (fu a) (gu b))

That’s the composition on objects, or types. Notice how in Haskell we apply type constructors to types, just like we apply functions to arguments. The syntax is the same.

If you’re getting a little lost, try applying BiComp to Either, Const (), Identity, a, and b, in this order. You will recover our bare-bone version of Maybe b (a is ignored).

The new data type BiComp is a bifunctor in a and b, but only if bf is itself a Bifunctor and fu and gu are Functors. The compiler must know that there will be a definition of bimap available for bf, and definitions of fmap for fu and gu. In Haskell, this is expressed as a precondition in the instance declaration: a set of class constraints followed by a double arrow:

instance (Bifunctor bf, Functor fu, Functor gu) =>
  Bifunctor (BiComp bf fu gu) where
    bimap f1 f2 (BiComp x) = BiComp ((bimap (fmap f1) (fmap f2)) x)

The implementation of bimap for BiComp is given in terms of bimap for bf and the two fmaps for fu and gu. The compiler automatically infers all the types and picks the correct overloaded functions whenever BiComp is used.

The x in the definition of bimap has the type:

bf (fu a) (gu b)

which is quite a mouthful. The outer bimap breaks through the outer bf layer, and the two fmaps dig under fu and gu, respectively. If the types of f1 and f2 are:

f1 :: a -> a'
f2 :: b -> b'

then the final result is of the type bf (fu a') (gu b'):

bimapbf :: (fu a -> fu a') -> (gu b -> gu b') 
  -> bf (fu a) (gu b) -> bf (fu a') (gu b')

If you like jigsaw puzzles, these kinds of type manipulations can provide hours of entertainment.

So it turns out that we didn’t have to prove that Maybe was a functor — this fact followed from the way it was constructed as a sum of two functorial primitives.

A perceptive reader might ask the question: If the derivation of the Functor instance for algebraic data types is so mechanical, can’t it be automated and performed by the compiler? Indeed, it can, and it is. You need to enable a particular Haskell extension by including this line at the top of your source file:

{-# LANGUAGE DeriveFunctor #-}

and then add deriving Functor to your data structure:

data Maybe a = Nothing | Just a
  deriving Functor

and the corresponding fmap will be implemented for you.

The regularity of algebraic data structures makes it possible to derive instances not only of Functor but of several other type classes, including the Eq type class I mentioned before. There is also the option of teaching the compiler to derive instances of your own typeclasses, but that’s a bit more advanced. The idea though is the same: You provide the behavior for the basic building blocks and sums and products, and let the compiler figure out the rest.

Functors in C++

If you are a C++ programmer, you obviously are on your own as far as implementing functors goes. However, you should be able to recognize some types of algebraic data structures in C++. If such a data structure is made into a generic template, you should be able to quickly implement fmap for it.

Let’s have a look at a tree data structure, which we would define in Haskell as a recursive sum type:

data Tree a = Leaf a | Node (Tree a) (Tree a)
    deriving Functor

As I mentioned before, one way of implementing sum types in C++ is through class hierarchies. It would be natural, in an object-oriented language, to implement fmap as a virtual function of the base class Functor and then override it in all subclasses. Unfortunately this is impossible because fmap is a template, parameterized not only by the type of the object it’s acting upon (the this pointer) but also by the return type of the function that’s been applied to it. Virtual functions cannot be templatized in C++. We’ll implement fmap as a generic free function, and we’ll replace pattern matching with dynamic_cast.

The base class must define at least one virtual function in order to support dynamic casting, so we’ll make the destructor virtual (which is a good idea in any case):

template<class T>
struct Tree {
    virtual ~Tree() {};
};

The Leaf is just an Identity functor in disguise:

template<class T>
struct Leaf : public Tree<T> {
    T _label;
    Leaf(T l) : _label(l) {}
};

The Node is a product type:

template<class T>
struct Node : public Tree<T> {
    Tree<T> * _left;
    Tree<T> * _right;
    Node(Tree<T> * l, Tree<T> * r) : _left(l), _right(r) {}
};

When implementing fmap we take advantage of dynamic dispatching on the type of the Tree. The Leaf case applies the Identity version of fmap, and the Node case is treated like a bifunctor composed with two copies of the Tree functor. As a C++ programmer, you’re probably not used to analyzing code in these terms, but it’s a good exercise in categorical thinking.

template<class A, class B>
Tree<B> * fmap(std::function<B(A)> f, Tree<A> * t)
{
    Leaf<A> * pl = dynamic_cast <Leaf<A>*>(t);
    if (pl)
        return new Leaf<B>(f (pl->_label));
    Node<A> * pn = dynamic_cast<Node<A>*>(t);
    if (pn)
        return new Node<B>( fmap<A>(f, pn->_left)
                          , fmap<A>(f, pn->_right));
    return nullptr;
}

For simplicity, I decided to ignore memory and resource management issues, but in production code you would probably use smart pointers (unique or shared, depending on your policy).

Compare it with the Haskell implementation of fmap:

instance Functor Tree where
    fmap f (Leaf a) = Leaf (f a)
    fmap f (Node t t') = Node (fmap f t) (fmap f t')

This implementation can also be automatically derived by the compiler.

The Writer Functor

I promised that I would come back to the Kleisli category I described earlier. Morphisms in that category were represented as “embellished” functions returning the Writer data structure.

type Writer a = (a, String)

I said that the embellishment was somehow related to endofunctors. And, indeed, the Writer type constructor is functorial in a. We don’t even have to implement fmap for it, because it’s just a simple product type.

But what’s the relation between a Kleisli category and a functor — in general? A Kleisli category, being a category, defines composition and identity. Let’ me remind you that the composition is given by the fish operator:

(>=>) :: (a -> Writer b) -> (b -> Writer c) -> (a -> Writer c)
m1 >=> m2 = \x -> 
    let (y, s1) = m1 x
        (z, s2) = m2 y
    in (z, s1 ++ s2)

and the identity morphism by a function called return:

return :: a -> Writer a
return x = (x, "")

It turns out that, if you look at the types of these two functions long enough (and I mean, long enough), you can find a way to combine them to produce a function with the right type signature to serve as fmap. Like this:

fmap f = id >=> (\x -> return (f x))

Here, the fish operator combines two functions: one of them is the familiar id, and the other is a lambda that applies return to the result of acting with f on the lambda’s argument. The hardest part to wrap your brain around is probably the use of id. Isn’t the argument to the fish operator supposed to be a function that takes a “normal” type and returns an embellished type? Well, not really. Nobody says that a in a -> Writer b must be a “normal” type. It’s a type variable, so it can be anything, in particular it can be an embellished type, like Writer b.

So id will take Writer a and turn it into Writer a. The fish operator will fish out the value of a and pass it as x to the lambda. There, f will turn it into a b and return will embellish it, making it Writer b. Putting it all together, we end up with a function that takes Writer a and returns Writer b, exactly what fmap is supposed to produce.

Notice that this argument is very general: you can replace Writer with any type constructor. As long as it supports a fish operator and return, you can define fmap as well. So the embellishment in the Kleisli category is always a functor. (Not every functor, though, gives rise to a Kleisli category.)

You might wonder if the fmap we have just defined is the same fmap the compiler would have derived for us with deriving Functor. Interestingly enough, it is. This is due to the way Haskell implements polymorphic functions. It’s called parametric polymorphism, and it’s a source of so called theorems for free. One of those theorems says that, if there is an implementation of fmap for a given type constructor, one that preserves identity, then it must be unique.

Covariant and Contravariant Functors

Now that we’ve reviewed the writer functor, let’s go back to the reader functor. It was based on the partially applied function-arrow type constructor:

(->) r

We can rewrite it as a type synonym:

type Reader r a = r -> a

for which the Functor instance, as we’ve seen before, reads:

instance Functor (Reader r) where
    fmap f g = f . g

But just like the pair type constructor, or the Either type constructor, the function type constructor takes two type arguments. The pair and Either were functorial in both arguments — they were bifunctors. Is the function constructor a bifunctor too?

Let’s try to make it functorial in the first argument. We’ll start with a type synonym — it’s just like the Reader but with the arguments flipped:

type Op r a = a -> r

This time we fix the return type, r, and vary the argument type, a. Let’s see if we can somehow match the types in order to implement fmap, which would have the following type signature:

fmap :: (a -> b) -> (a -> r) -> (b -> r)

With just two functions taking a and returning, respectively, b and r, there is simply no way to build a function taking b and returning r! It would be different if we could somehow invert the first function, so that it took b and returned a instead. We can’t invert an arbitrary function, but we can go to the opposite category.

A short recap: For every category C there is a dual category C^op. It’s a category with the same objects as C, but with all the arrows reversed.

Consider a functor that goes between C^op and some other category D:
F :: C^op → D
Such a functor maps a morphism f^op :: a → b in C^op to the morphism F f^op :: F a → F b in D. But the morphism f^op secretly corresponds to some morphism f :: b → a in the original category C. Notice the inversion.

Now, F is a regular functor, but there is another mapping we can define based on F, which is not a functor — let’s call it G. It’s a mapping from C to D. It maps objects the same way F does, but when it comes to mapping morphisms, it reverses them. It takes a morphism f :: b → a in C, maps it first to the opposite morphism f^op :: a → b and then uses the functor F on it, to get F f^op :: F a → F b.

Considering that F a is the same as G a and F b is the same as G b, the whole trip can be described as:
G f :: (b → a) → (G a → G b)
It’s a “functor with a twist.” A mapping of categories that inverts the direction of morphisms in this manner is called a contravariant functor. Notice that a contravariant functor is just a regular functor from the opposite category. The regular functors, by the way — the kind we’ve been studying thus far — are called covariant functors.

Here’s the typeclass defining a contravariant functor (really, a contravariant endofunctor) in Haskell:

class Contravariant f where
    contramap :: (b -> a) -> (f a -> f b)

Our type constructor Op is an instance of it:

instance Contravariant (Op r) where
    -- (b -> a) -> Op r a -> Op r b
    contramap f g = g . f

Notice that the function f inserts itself before (that is, to the right of) the contents of Op — the function g.

The definition of contramap for Op may be made even terser, if you notice that it’s just the function composition operator with the arguments flipped. There is a special function for flipping arguments, called flip:

flip :: (a -> b -> c) -> (b -> a -> c)
flip f y x = f x y

With it, we get:

contramap = flip (.)

Profunctors

We’ve seen that the function-arrow operator is contravariant in its first argument and covariant in the second. Is there a name for such a beast? It turns out that, if the target category is Set, such a beast is called a profunctor. Because a contravariant functor is equivalent to a covariant functor from the opposite category, a profunctor is defined as:
C^op × D → Set

Since, to first approximation, Haskell types are sets, we apply the name Profunctor to a type constructor p of two arguments, which is contra-functorial in the first argument and functorial in the second. Here’s the appropriate typeclass taken from the Data.Profunctor library:

class Profunctor p where
  dimap :: (a -> b) -> (c -> d) -> p b c -> p a d
  dimap f g = lmap f . rmap g
  lmap :: (a -> b) -> p b c -> p a c
  lmap f = dimap f id
  rmap :: (b -> c) -> p a b -> p a c
  rmap = dimap id

All three functions come with default implementations. Just like with Bifunctor, when declaring an instance of Profunctor, you have a choice of either implementing dimap and accepting the defaults for lmap and rmap, or implementing both lmap and rmap and accepting the default for dimap.

Now we can assert that the function-arrow operator is an instance of a Profunctor:

instance Profunctor (->) where
  dimap ab cd bc = cd . bc . ab
  lmap = flip (.)
  rmap = (.)

Profunctors have their application in the Haskell lens library. We’ll see them again when we talk about ends and coends.

The Hom-Functor

The above examples are the reflection of a more general statement that the mapping that takes a pair of objects a and b and assigns to it the set of morphisms between them, the hom-set C(a, b), is a functor. It is a functor from the product category C^op×C to the category of sets, Set.

Let’s define its action on morphisms. A morphism in C^op×C is a pair of morphisms from C:

f :: a'→ a
g :: b → b'

The lifting of this pair must be a morphism (a function) from the set C(a, b) to the set C(a', b'). Just pick any element h of C(a, b) (it’s a morphism from a to b) and assign to it:

g ∘ h ∘ f

which is an element of C(a', b').

As you can see, the hom-functor is a special case of a profunctor.

Challenges

1. Show that the data type:

   data Pair a b = Pair a b

   is a bifunctor. For additional credit implement all three methods of Bifunctor and use equational reasoning to show that these definitions are compatible with the default implementations whenever they can be applied.

2. Show the isomorphism between the standard definition of Maybe and this desugaring:

   type Maybe' a = Either (Const () a) (Identity a)

   Hint: Define two mappings between the two implementations. For additional credit, show that they are the inverse of each other using equational reasoning.

3. Let’s try another data structure. I call it a PreList because it’s a precursor to a List. It replaces recursion with a type parameter b.

   data PreList a b = Nil | Cons a b

   You could recover our earlier definition of a List by recursively applying PreList to itself (we’ll see how it’s done when we talk about fixed points).

   Show that PreList is an instance of Bifunctor.

4. Show that the following data types define bifunctors in a and b:

   data K2 c a b = K2 c

   data Fst a b = Fst a

   data Snd a b = Snd b

   For additional credit, check your solutions agains Conor McBride’s paper Clowns to the Left of me, Jokers to the Right.

5. Define a bifunctor in a language other than Haskell. Implement bimap for a generic pair in that language.
6. Should std::map be considered a bifunctor or a profunctor in the two template arguments Key and T? How would you redesign this data type to make it so?

Next: Function Types.

Acknowledgment

As usual, big thanks go to Gershom Bazerman for reviewing this article.
Follow @BartoszMilewski