There is an exercise in Saunders Mac Lane’s “Categories for the Working Mathematician” that was a lesson in humility for me. Despite several hints provided by Mac Lane, all my attempts to solve it failed. Finally my Internet search led me to a diagram that looked promissing and it allowed me to crack the problem.

Why do I think this is interesting? Because it shows the kind of pattern matching and shape shifting that is characteristic of categorical proofs. The key is the the use of visual representations and the ability to progressively hide the details under the terseness of notation until the big picture emerges.

The Exercise

This is, slightly parapharased, exercise 1.1 in chapter VII, Monoids:

Prove that the pentagon identity and the triangle identity imply:
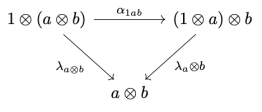
Problem

First, let me explain what it all means. We are working in a monoidal category, that is a category with a tensor product. Given two objects a and b, we can construct their product a \otimes b. Similarly, given two arrows f \colon a \to b and g \colon a' \to b', we can construct an arrow

f \otimes g \colon a \otimes b \to a' \otimes b'

In other words, \otimes is a (bi-)functor.

There is a special object 1 that serves as a unit with respect to the tensor product. But, since in category theory we shy away from equalities on objects, the unit laws are not equalities, but rather natural isomorphisms, whose components are:

\lambda_a \colon 1 \otimes a \to a

\rho_a \colon a \otimes 1 \to a

These transformations are called, respecively, the left and right unitors. We’ll come back to naturality later, when we have to use it in anger.

We want the tensor product to be associative, again using a natural isomorphism called the associator:

\alpha_{a b c} \colon a \otimes (b \otimes c) \to (a \otimes b) \otimes c

The components of natural transformations are just regular arrows, so we can tensor them. In particular, we can tensor a left unitor \lambda_a with an identity natural transformation \text{id} to get:

\lambda_a \otimes \text{id}_b \colon (1 \otimes a) \otimes b \to a \otimes b

Since tensoring with identity is a common operation, it has a name “whiskering,” and is abbreviated to \lambda_a \otimes b. Any time you see a natural transformation tensored with an object, it’s a shorthand for whiskering.

You are now well equipped to understand the diagram from the exercise.
Problem
The goal is to prove that it commutes, that is:

\lambda_{a \otimes b} = (\lambda_a \otimes b) \circ \alpha_{1 a b}

From now on, in the spirit of terseness, I will be mostly omitting the tensor sign, so the above will be written as:

\lambda_{a b} = \lambda_a b \circ \alpha_{1 a b}

Since most of the proof revolves around different ways of parenthesising multiple tensor products, I will use a simple, self explanatory graphical language, where parenthesized products are represented by binary trees. Using trees will help us better recognize shapes and patterns.
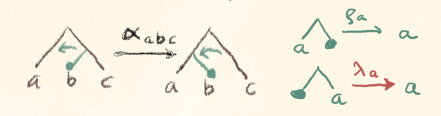
Associativity and Unit Laws
The associator flips a switch, and the unitors absorb the unit, which is represented by a green blob.

In tree notation, our goal is to show that the following diagram commutes:
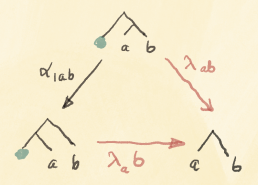
The Problem

We also assume that the associator and the unitors satisfy some laws: the pentagon identity and the triangle identity. I will introduce them as needed.

The Pentagon

The first hint that Mac Lane gives us is to start with the pentagon identity, which normally involves four arbitrary objects, and replace the first two objects with the unit. The result is this commuting diagram:

It shows that the two ways of flipping the parentheses from 1 (1 (a b)) to ((1 1) a) b) are equivalent. As a reminder, the notation \alpha_{1 1 a} b at the bottom means: hold the rightmost b while applying \alpha to the inner tree. This is an example of whiskering.

The Right Unitor

The second hint is a bit confusing. Mac Lane asks us to add \rho in two places. But all the trees have the unit objects in the two leftmost positions, so surely he must have meant \lambda. I was searching for some kind of an online errata, but none was found. However, if you look closely, there are two potential sites where the right unitor could be applied, notwithstanding the fact that it has another unit to its left. So that must be it!

In both cases, we use the component \rho_1 \colon 1 \otimes 1 \to 1. In the first case, we hold the product (a \otimes b) unchanged. In the second case we whisker \rho_1 with a and then whisker the result with b.

Triangle Identity

The next hint tells us to use the triangle identity. Here’s this identity in diagram notation:
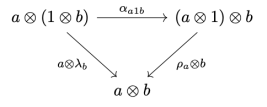
TriangleId
And here it is in tree notation:

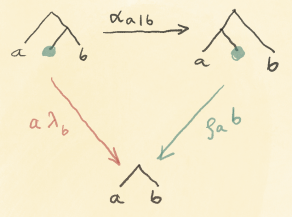
Triangle
We interpret this as: if you have the unit in the middle, you can associate it to the right or to the left and then use the appropriate unitor. The result in both cases is the same.

It’s not immediately obvious where and how to apply this pattern. We will definitely have to do some squinting.

In the first occurrence of \rho in our pentagon, we have \rho_1 \otimes (a \otimes b). To apply the triangle identity, we have to do two substitutions in it. We have to use 1 as the left object and (a \otimes b) as the right object.

In the second instance, we perform a different trick: we hold the rightmost b in place and apply the triangle identity to the inner triple (1, 1, a).

Naturality

Keep in mind our goal:
The Problem
You can almost see it emerging in the upper left corner of the pentagon. In fact the three trees there are what we want, except that they are all left-multiplied by the unit. All we need is to connect the dots using commuting diagrams.

Focus on the two middle trees: they differ only by associativity, so we can connect them using \alpha_{1 a b}:

But how do we know that the quadrilateral we have just completed commutes? Here, Mac Lane offers another hint: use suitable naturalities.

In general, naturality means that the following square commutes:
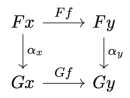
Screenshot 2023-09-14 at 18.42.40
Here, we have a natural transformation \alpha between two functors F and G; and the arrow f \colon a \to b is lifted by each in turn.

Now compare this with the quadrilateral we have in our diagram:
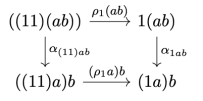
Screenshot 2023-09-14 at 18.43.09
If you stare at these two long enough, you’ll discover that you can indeed identify two functors, both parameterized by a pair of objects a and b:

F_{a b} x = x (a b)

G_{a b} x = (x a) b

We get:
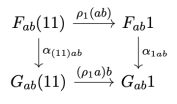
Screenshot 2023-09-14 at 18.42.59

The natural transformation in question is the associator \alpha_{x a b}. We are using its naturality in the first argument, keeping the two others constant. The arrow we are lifting is \rho_1 \colon 1 \otimes 1 \to 1. The first functor lifts it to \rho_1 (a b), and the second one to (\rho_1 a) b.

Thus we have successfully shrunk our commuting pentagon.

The Left Unitor

We are now ready to carve out another quadrilateral using the twice-whiskered left unitor 1 (\lambda_a b).

Again, we use naturality, this time in the middle argument of \alpha.
Nat2
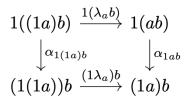
The two functors are:

F_b x = 1 (x b)

G_b x = (1 x) b

and the arrow we’re lifting is \lambda_a.

The Shrinking Triangle

We have successfully shrunk the pentagon down to a triangle. What remains to reach our goal is now to shrink this triangle. We can do this by applying \lambda three times:

More Naturality

The final step is to connect the three vertices to form our target triangle.

This time we use the naturality of \lambda to show that the three quadrilaterals commute. (I recommend this as an exercise.)

Since we started with a commuting pentagon, and all the triangles and quadrilaterals that we used to shrink it commute, and all the arrows are reversible, the inner triangle must commute as well. This completes the proof.

Conclusion

I don’t think it’s possible to do category theory without drawing pictures. Sure, Mac Lane’s pentagon diagram can be written as an algebraic equation:

\alpha_{(a \otimes b) c d} \circ \alpha_{a b (c \otimes d)} = (\alpha_{a b c} \otimes d) \circ \alpha_{a (b \otimes c) d} \circ (a \otimes \alpha_{b c d})

In programming we would call this point-free encoding and consider an aberration. Unfortunately, this is exactly the language of proof assistants like Lean, Agda, or Coq. No wonder it takes forever for mathematicians to formalize their theories. We really need proof assistants that work with diagrams.

Incidentally, the tools that mathematicians use today to publish diagrams are extremely primitive. Some of the simpler diagrams in this blog post were done using a latex plugin called tikz-cd, but to draw the more complex ones I had to switch to an iPad drawing tool called ProCreate, which is way more user friendly. (I also used it to make the drawing below.)