This is part 14 of Categories for Programmers. Previously: Free Monoids. See the Table of Contents.

It’s about time we had a little talk about sets. Mathematicians have a love/hate relationship with set theory. It’s the assembly language of mathematics — at least it used to be. Category theory tries to step away from set theory, to some extent. For instance, it’s a known fact that the set of all sets doesn’t exist, but the category of all sets, Set, does. So that’s good. On the other hand, we assume that morphisms between any two objects in a category form a set. We even called it a hom-set. To be fair, there is a branch of category theory where morphisms don’t form sets. Instead they are objects in another category. Those categories that use hom-objects rather than hom-sets, are called enriched categories. In what follows, though, we’ll stick to categories with good old-fashioned hom-sets.

A set is the closest thing to a featureless blob you can get outside of categorical objects. A set has elements, but you can’t say much about these elements. If you have a finite set, you can count the elements. You can kind of count the elements of an inifinite set using cardinal numbers. The set of natural numbers, for instance, is smaller than the set of real numbers, even though both are infinite. But, maybe surprisingly, a set of rational numbers is the same size as the set of natural numbers.

Other than that, all the information about sets can be encoded in functions between them — especially the invertible ones called isomorphisms. For all intents and purposes isomorphic sets are identical. Before I summon the wrath of foundational mathematicians, let me explain that the distinction between equality and isomorphism is of fundamental importance. In fact it is one of the main concerns of the latest branch of mathematics, the Homotopy Type Theory (HoTT). I’m mentioning HoTT because it’s a pure mathematical theory that takes inspiration from computation, and one of its main proponents, Vladimir Voevodsky, had a major epiphany while studying the Coq theorem prover. The interaction between mathematics and programming goes both ways.

The important lesson about sets is that it’s okay to compare sets of unlike elements. For instance, we can say that a given set of natural transformations is isomorphic to some set of morphisms, because a set is just a set. Isomorphism in this case just means that for every natural transformation from one set there is a unique morphism from the other set and vice versa. They can be paired against each other. You can’t compare apples with oranges, if they are objects from different categories, but you can compare sets of apples against sets of oranges. Often transforming a categorical problem into a set-theoretical problem gives us the necessary insight or even lets us prove valuable theorems.

The Hom Functor

Every category comes equipped with a canonical family of mappings to Set. Those mappings are in fact functors, so they preserve the structure of the category. Let’s build one such mapping.

Let’s fix one object a in C and pick another object x also in C. The hom-set C(a, x) is a set, an object in Set. When we vary x, keeping a fixed, C(a, x) will also vary in Set. Thus we have a mapping from x to Set.

If we want to stress the fact that we are considering the hom-set as a mapping in its second argument, we use the notation:

C(a, -)

with the dash serving as the placeholder for the argument.

This mapping of objects is easily extended to the mapping of morphisms. Let’s take a morphism f in C between two arbitrary objects x and y. The object x is mapped to the set C(a, x), and the object y is mapped to C(a, y), under the mapping we have just defined. If this mapping is to be a functor, f must be mapped to a function between the two sets:

C(a, x) -> C(a, y)

Let’s define this function point-wise, that is for each argument separately. For the argument we should pick an arbitrary element of C(a, x) — let’s call it h. Morphisms are composable, if they match end to end. It so happens that the target of h matches the source of f, so their composition:

f ∘ h :: a -> y

is a morphism going from a to y. It is therefore a member of C(a, y).

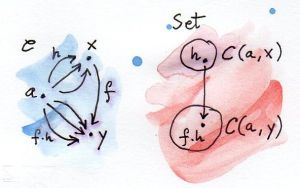
We have just found our function from C(a, x) to C(a, y), which can serve as the image of f. If there is no danger of confusion, we’ll write this lifted function as:

C(a, f)

and its action on a morphism h as:

C(a, f) h = f ∘ h

Since this construction works in any category, it must also work in the category of Haskell types. In Haskell, the hom-functor is better known as the Reader functor:

type Reader a x = a -> x

instance Functor (Reader a) where
    fmap f h = f . h

Now let’s consider what happens if, instead of fixing the source of the hom-set, we fix the target. In other words, we’re asking the question if the mapping

C(-, a)

is also a functor. It is, but instead of being covariant, it’s contravariant. That’s because the same kind of matching of morphisms end to end results in postcomposition by f; rather than precomposition, as was the case with C(a, -).

We have already seen this contravariant functor in Haskell. We called it Op:

type Op a x = x -> a

instance Contravariant (Op a) where
    contramap f h = h . f

Finally, if we let both objects vary, we get a profunctor C(-, =), which is contravariant in the first argument and covariant in the second (to underline the fact that the two arguments may vary independently, we use a double dash as the second placeholder). We have seen this profunctor before, when we talked about functoriality:

instance Profunctor (->) where
  dimap ab cd bc = cd . bc . ab
  lmap = flip (.)
  rmap = (.)

The important lesson is that this observation holds in any category: the mapping of objects to hom-sets is functorial. Since contravariance is equivalent to a mapping from the opposite category, we can state this fact succintly as:

C(-, =) :: Cop × C -> Set

Representable Functors

We’ve seen that, for every choice of an object a in C, we get a functor from C to Set. This kind of structure-preserving mapping to Set is often called a representation. We are representing objects and morphisms of C as sets and functions in Set.

The functor C(a, -) itself is sometimes called representable. More generally, any functor F that is naturally isomorphic to the hom-functor, for some choice of a, is called representable. Such functor must necessarily be Set-valued, since C(a, -) is.

I said before that we often think of isomorphic sets as identical. More generally, we think of isomorphic objects in a category as identical. That’s because objects have no structure other than their relation to other objects (and themselves) through morphisms.

For instance, we’ve previously talked about the category of monoids, Mon, that was initially modeled with sets. But we were careful to pick as morphisms only those functions that preserved the monoidal structure of those sets. So if two objects in Mon are isomorphic, meaning there is an invertible morphism between them, they have exactly the same structure. If we peeked at the sets and functions that they were based upon, we’d see that the unit element of one monoid was mapped to the unit element of another, and that a product of two elements was mapped to the product of their mappings.

The same reasoning can be applied to functors. Functors between two categories form a category in which natural transformations play the role of morphisms. So two functors are isomorphic, and can be thought of as identical, if there is an invertible natural transformation between them.

Let’s analyze the definition of the representable functor from this perspective. For F to be representable we require that: There be an object a in C; one natural transformation α from C(a, -) to F; another natural transformation, β, in the opposite direction; and that their composition be the identity natural transformation.

Let’s look at the component of α at some object x. It’s a function in Set:

αx :: C(a, x) -> F x

The naturality condition for this transformation tells us that, for any morphism f from x to y, the following diagram commutes:

F f ∘ αx = αy ∘ C(a, f)

In Haskell, we would replace natural transformations with polymorphic functions:

alpha :: forall x. (a -> x) -> F x

with the optional forall quantifier. The naturality condition

fmap f . alpha = alpha . fmap f

is automatically satisfied due to parametricity (it’s one of those theorems for free I mentioned earlier), with the understanding that fmap on the left is defined by the functor F, whereas the one on the right is defined by the reader functor. Since fmap for reader is just function precomposition, we can be even more explicit. Acting on h, an element of C(a, x), the naturality condition simplifies to:

fmap f (alpha h) = alpha (f . h)

The other transformation, beta, goes the opposite way:

beta :: forall x. F x -> (a -> x)

It must respect naturality conditions, and it must be the inverse of α:

α ∘ β = id = β ∘ α

We will see later that a natural transformation from C(a, -) to any Set-valued functor always exists, as long as F a is non-empty (Yoneda’s lemma) but it’s not necessarily invertible.

Let me give you an example in Haskell with the list functor and Int as a. Here’s a natural transformation that does the job:

alpha :: forall x. (Int -> x) -> [x]
alpha h = map h [12]

I have arbitrarily picked the number 12 and created a singleton list with it. I can then fmap the function h over this list and get a list of the type returned by h. (There are actually as many such transformations as there are list of integers.)

The naturality condition is equivalent to the composability of map (the list version of fmap):

map f (map h [12]) = map (f . h) [12]

But if we tried to find the inverse transformation, we would have to go from a list of arbitrary type x to a function returning x:

beta :: forall x. [x] -> (Int -> x)

You might think of retrieving an x from the list, e.g., using head, but that won’t work for an empty list. Notice that there is no choice for the type a (in place of Int) that would work here. So the list functor is not representable.

Remember when we talked about Haskell (endo-) functors being a little like containers? In the same vein we can think of representable functors as containers for storing memoized results of function calls (the members of hom-sets in Haskell are just functions). The representing object, the type a in C(a, -), is thought of as the key type, with which we can access the tabulated values of a function. The transformation we called α is called tabulate, and its inverse, β, is called index. Here’s a (slightly simplified) Representable class definition:

class Representable f where
   type Rep f :: *
   tabulate :: (Rep f -> x) -> f x
   index    :: f x -> Rep f -> x

Notice that the representing type, our a, which is called Rep f here, is part of the definition of Representable. The star just means that Rep f is a type (as opposed to a type constructor, or other more exotic kinds).

Infinite lists, or streams, which cannot be empty, are representable.

data Stream x = Cons x (Stream x)

You can think of them as memoized values of a function taking an Integer as an argument. (Strictly speaking, I should be using non-negative natural numbers, but I didn’t want to complicate the code.)

To tabulate such a function, you create an infinite stream of values. Of course, this is only possible because Haskell is lazy. The values are evaluated on demand. You access the memoized values using index:

instance Representable Stream where
    type Rep Stream = Integer
    tabulate f = Cons (f 0) (tabulate (f . (+1)))
    index (Cons b bs) n = if n == 0 then b else index bs (n - 1)

It’s interesting that you can implement a single memoization scheme to cover a whole family of functions with arbitrary return types.

Representability for contravariant functors is similarly defined, except that we keep the second argument of C(-, a) fixed. Or, equivalently, we may consider functors from C^op to Set, because Cop(a, -) is the same as C(-, a).

There is an interesting twist to representability. Remember that hom-sets can internally be treated as exponential objects, in cartesian closed categories. The hom-set C(a, x) is equivalent to xa, and for a representable functor F we can write:

-a = F

Let’s take the logarithm of both sides, just for kicks:

a = log F

Of course, this is a purely formal transformation, but if you know some of the properties of logarithms, it is quite helpful. In particular, it turns out that functors that are based on product types can be represented with sum types, and that sum-type functors are not in general representable (example: the list functor).

Finally, notice that a representable functor gives us two different implementations of the same thing — one a function, one a data structure. They have exactly the same content — the same values are retrieved using the same keys. That’s the sense of “sameness” I was talking about. Two naturally isomorphic functors are identical as far as their contents are involved. On the other hand, the two representations are often implemented differently and may have different performance characteristics. Memoization is used as a performance enhancement and may lead to substantially reduced run times. Being able to generate different representations of the same underlying computation is very valuable in practice. So, surprisingly, even though it’s not concerned with performance at all, category theory provides ample opportunities to explore alternative implementations that have practical value.

Challenges

1. Show that the hom-functors map identity morphisms in C to corresponding identity functions in Set.
2. Show that Maybe is not representable.
3. Is the Reader functor representable?
4. Using Stream representation, memoize a function that squares its argument.
5. Show that tabulate and index for Stream are indeed the inverse of each other. (Hint: use induction.)
6. The functor:

   Pair a = Pair a a

   is representable. Can you guess the type that represents it? Implement tabulate and index.

Bibliography

1. The Catsters video about representable functors.

Next: The Yoneda Lemma.

Acknowledgments

I’d like to thank Gershom Bazerman for checking my math and logic, and André van Meulebrouck, who has been volunteering his editing help throughout this series of posts.
Follow @BartoszMilewski

This is part 13 of Categories for Programmers. Previously: Limits and Colimits. See the Table of Contents.

Monoids are an important concept in both category theory and in programming. Categories correspond to strongly typed languages, monoids to untyped languages. That’s because in a monoid you can compose any two arrows, just as in an untyped language you can compose any two functions (of course, you may end up with a runtime error when you execute your program).

We’ve seen that a monoid may be described as a category with a single object, where all logic is encoded in the rules of morphism composition. This categorical model is fully equivalent to the more traditional set-theoretical definition of a monoid, where we “multiply” two elements of a set to get a third element. This process of “multiplication” can be further dissected into first forming a pair of elements and then identifying this pair with an existing element — their “product.”

What happens when we forgo the second part of multiplication — the identification of pairs with existing elements? We can, for instance, start with an arbitrary set, form all possible pairs of elements, and call them new elements. Then we’ll pair these new elements with all possible elements, and so on. This is a chain reaction — we’ll keep adding new elements forever. The result, an infinite set, will be almost a monoid. But a monoid also needs a unit element and the law of associativity. No problem, we can add a special unit element and identify some of the pairs — just enough to support the unit and associativity laws.

Let’s see how this works in a simple example. Let’s start with a set of two elements, {a, b}. We’ll call them the generators of the free monoid. First, we’ll add a special element e to serve as the unit. Next we’ll add all the pairs of elements and call them “products”. The product of a and b will be the pair (a, b). The product of b and a will be the pair (b, a), the product of a with a will be (a, a), the product of b with b will be (b, b). We can also form pairs with e, like (a, e), (e, b), etc., but we’ll identify them with a, b, etc. So in this round we’ll only add (a, a), (a, b) and (b, a) and (b, b), and end up with the set {e, a, b, (a, a), (a, b), (b, a), (b, b)}.

In the next round we’ll keep adding elements like: (a, (a, b)), ((a, b), a), etc. At this point we’ll have to make sure that associativity holds, so we’ll identify (a, (b, a)) with ((a, b), a), etc. In other words, we won’t be needing internal parentheses.

You can guess what the final result of this process will be: we’ll create all possible lists of as and bs. In fact, if we represent e as an empty list, we can see that our “multiplication” is nothing but list concatenation.

This kind of construction, in which you keep generating all possible combinations of elements, and perform the minimum number of identifications — just enough to uphold the laws — is called a free construction. What we have just done is to construct a free monoid from the set of generators {a, b}.

Free Monoid in Haskell

A two-element set in Haskell is equivalent to the type Bool, and the free monoid generated by this set is equivalent to the type [Bool] (list of Bool). (I am deliberately ignoring problems with infinite lists.)

A monoid in Haskell is defined by the type class:

class Monoid m where
    mempty  :: m
    mappend :: m -> m -> m

This just says that every Monoid must have a neutral element, which is called mempty, and a binary function (multiplication) called mappend. The unit and associativity laws cannot be expressed in Haskell and must be verified by the programmer every time a monoid is instantiated.

The fact that a list of any type forms a monoid is described by this instance definition:

instance Monoid [a] where
    mempty  = []
    mappend = (++)

It states that an empty list [] is the unit element, and list concatenation (++) is the binary operation.

As we have seen, a list of type a corresponds to a free monoid with the set a serving as generators. The set of natural numbers with multiplication is not a free monoid, because we identify lots of products. Compare for instance:

2 * 3 = 6
[2] ++ [3] = [2, 3] // not the same as [6]

That was easy, but the question is, can we perform this free construction in category theory, where we are not allowed to look inside objects? We’ll use our workhorse: the universal construction.

The second interesting question is, can any monoid be obtained from some free monoid by identifying more than the minimum number of elements required by the laws? I’ll show you that this follows directly from the universal construction.

Free Monoid Universal Construction

If you recall our previous experiences with universal constructions, you might notice that it’s not so much about constructing something as about selecting an object that best fits a given pattern. So if we want to use the universal construction to “construct” a free monoid, we have to consider a whole bunch of monoids from which to pick one. We need a whole category of monoids to chose from. But do monoids form a category?

Let’s first look at monoids as sets equipped with additional structure defined by unit and multiplication. We’ll pick as morphisms those functions that preserve the monoidal structure. Such structure-preserving functions are called homomorphisms. A monoid homomorphism must map the product of two elements to the product of the mapping of the two elements:

h (a * b) = h a * h b

and it must map unit to unit.
For instance, consider a homomorphism from lists of integers to integers. If we map [2] to 2 and [3] to 3, we have to map [2, 3] to 6, because concatenation

[2] ++ [3] = [2, 3]

becomes multiplication

2 * 3 = 6

Now let’s forget about the internal structure of individual monoids, and only look at them as objects with corresponding morphisms. You get a category Mon of monoids.

Okay, maybe before we forget about internal structure, let us notice an important property. Every object of Mon can be trivially mapped to a set. It’s just the set of its elements. This set is called the underlying set. In fact, not only can we map objects of Mon to sets, but we can also map morphisms of Mon (homomorphisms) to functions. Again, this seems sort of trivial, but it will become useful soon. This mapping of objects and morphisms from Mon to Set is in fact a functor. Since this functor “forgets” the monoidal structure — once we are inside a plain set, we no longer distinguish the unit element or care about multiplication — it’s called a forgetful functor. Forgetful functors come up regularly in category theory.

We now have two different views of Mon. We can treat it just like any other category with objects and morphisms. In that view, we don’t see the internal structure of monoids. All we can say about a particular object in Mon is that it connects to itself and to other objects through morphisms. The “multiplication” table of morphisms — the composition rules — are derived from the other view: monoids-as-sets. By going to category theory we haven’t lost this view completely — we can still access it through our forgetful functor.

To apply the universal construction, we need to define a special property that would let us search through the category of monoids and pick the best candidate for a free monoid. But a free monoid is defined by its generators. Different choices of generators produce different free monoids (a list of Bool is not the same as a list of Int). Our construction must start with a set of generators. So we’re back to sets!

That’s where the forgetful functor comes into play. We can use it to X-ray our monoids. We can identify the generators in the X-ray images of those blobs. Here’s how it works:

We start with a set of generators, x. That’s a set in Set.

The pattern we are going to match consists of a monoid m — an object of Mon — and a function p in Set:

p :: x -> U m

where U is our forgetful functor from Mon to Set. This is a weird heterogeneous pattern — half in Mon and half in Set.

The idea is that the function p will identify the set of generators inside the X-ray image of m. It doesn’t matter that functions may be lousy at identifying points inside sets (they may collapse them). It will all be sorted out by the universal construction, which will pick the best representative of this pattern.

We also have to define the ranking among candidates. Suppose we have another candidate: a monoid n and a function that identifies the generators in its X-ray image:

q :: x -> U n

We’ll say that m is better than n if there is a morphism of monoids (that’s a structure-preserving homomorphism):

h :: m -> n

whose image under U (remember, U is a functor, so it maps morphisms to functions) factorizes through p:

q = U h . p

If you think of p as selecting the generators in m; and q as selecting “the same” generators in n; then you can think of h as mapping these generators between the two monoids. Remember that h, by definition, preserves the monoidal structure. It means that a product of two generators in one monoid will be mapped to a product of the corresponding two generators in the second monoid, and so on.

This ranking may be used to find the best candidate — the free monoid. Here’s the definition:

We’ll say that m (together with the function p) is the free monoid with the generators x if and only if there is a unique morphism h from m to any other monoid n (together with the function q) that satisfies the above factorization property.

Incidentally, this answers our second question. The function U h is the one that has the power to collapse multiple elements of U m to a single element of U n. This collapse corresponds to identifying some elements of the free monoid. Therefore any monoid with generators x can be obtained from the free monoid based on x by identifying some of the elements. The free monoid is the one where only the bare minimum of identifications have been made.

We’ll come back to free monoids when we talk about adjunctions.

Challenges

1. You might think (as I did, originally) that the requirement that a homomorphism of monoids preserve the unit is redundant. After all, we know that for all a

   h a * h e = h (a * e) = h a

   So h e acts like a right unit (and, by analogy, as a left unit). The problem is that h a, for all a might only cover a sub-monoid of the target monoid. There may be a “true” unit outside of the image of h. Show that an isomorphism between monoids that preserves multiplication must automatically preserve unit.

2. Consider a monoid homomorphism from lists of integers with concatenation to integers with multiplication. What is the image of the empty list []? Assume that all singleton lists are mapped to the integers they contain, that is [3] is mapped to 3, etc. What’s the image of [1, 2, 3, 4]? How many different lists map to the integer 12? Is there any other homomorphism between the two monoids?
3. What is the free monoid generated by a one-element set? Can you see what it’s isomorphic to?

Next: Representable Functors.

Acknowledgments

I’d like to thank Gershom Bazerman for checking my math and logic, and André van Meulebrouck, who has been volunteering his editing help throughout this series of posts.
Follow @BartoszMilewski

Lenses are a fascinating subject. Edward Kmett’s lens library is an indispensable tool in every Haskell programmer’s toolbox. I set out to write this blog post with the goal of describing some new insights into their categorical interpretation, but then I started reviewing all the different formulations of lenses and their relations to each other. So this post turned into a little summary of the theoretical underpinning of lenses.

If you’re already familiar with lenses, you may skip directly to the last section, which describes some new results.

The Data-Centric Picture

Lenses start as a very simple idea: an accessor/mutator or getter/setter pair — something familiar to every C++, Java, or C# programmer. In Haskell they can be described as two functions:

get :: s -> a
set :: s -> a -> s

Given an object of type s, the first function produces the value of the object’s sub-component of type a — which is the focus of the particular lens. The second function takes the object together with a new value for the sub-component, and produces a modified object.

A simple example is a lens that focuses on the first component of a pair:

get :: (a, a') -> a
get (x, y) = x

set :: (a, a') -> a -> (a, a')
set (x, y) x' = (x', y)

In Haskell we can go even further and define a lens for a polymorphic object, in which the setter changes not only the value of the sub-component, but also its type. This will, of course, also change the type of the resulting object. So, in general we have:

get :: s -> a
set :: s -> b -> t

Our pair example doesn’t change much on the surface:

get :: (a, a') -> a
get (x, y) = x

set :: (a, a') -> b -> (b, a')
set (x, y) x' = (x', y)

The difference is that the type of x' can now be different from the type of x. The first component of the pair is of type a before the update, and of type b (the same as that of x') after it. This way we can turn a pair of, say, (Int, Bool) to a pair of (String, Bool).

We can always go back to the monomorphic version of the lens by choosing b equal to a and t equal to s.

Not every pair of functions like these constitutes a lens. A lens has to obey a few laws (first formulated by Pierce in the database context). In particular, if you get a component after you set it, you should get back the value you just put in:

get . set s = id

If you call set with the value you obtained from get, you should get back the unchanged object:

set s (get s) = s

Finally, a set should overwrite the result of a previous set:

set (set s a) b = set s b

So this is what I would call a “classical” lens. It’s formulated in easy to understand programming terms.

The Algebraic Picture

It was Russell O’Connor who noticed that when you refactor the common element from the getter/setter pair, you get an interesting algebraic structure. Instead of writing the lens as two functions, we can write it as one function returning a pair:

s -> (a, b -> t)

Think of this as factoring out the “this” pointer in OO and returning the interface. Of course, the difference is that, in functional programming, the setter does not mutate the original — it returns a new version of the object instead.

Let’s for a moment concentrate on the monomorphic version of the lens — one in which a is the same as b, and s is the same as t. We can define a data structure:

data Store a s = Store a (a -> s)

and rewrite the lens as:

s -> Store a s

For instance, our first-component-of-a-pair lens will take the form:

fstl :: (a, b) -> Store a (a, b)
fstl (x, y) = Store x (\x' -> (x', y))

The first observation is that, for any a, Store a is a functor:

instance Functor (Store a) where
    fmap f (Store x h) = Store x (f . h)

It’s a well-known fact that you can define algebras for a functor, so-called F-algebras. An algebra for a functor f consists of a type s called the carrier type and a function called the action:

alg :: f s -> s

This is almost like a lens (with f replaced by Store a), except that the arrow goes the wrong way. Not to worry: there is a dual notion called a coalgebra. It consists of a carrier type s and a function:

coalg :: s -> f s

Substitute Store a for f and you see that a lens is nothing but a coalgebra for this functor. This is not saying much — we have just given a mathematical name to a programming construct, no big deal. Except that Store a is more than a functor — it’s also a comonad.

What’s a comonad? It’s a monad with the arrows reversed.

You know that you can define a monad in Haskell using return and join. Reverse the arrows on those two, and you get extract and duplicate, the two functions that define a comonad.

class (Functor w) => Comonad w where
    extract :: w a -> a
    duplicate :: w a -> w (w a)

Here, w is a type constructor that is also a functor.

This is how you can implement those two functions for Store a:

instance Comonad (Store a) where
    -- extract :: Store a s -> s
    extract (Store x h) = h x
    -- duplicate :: Store a s -> Store a (Store a s)
    duplicate (Store x h) = Store x (\y -> Store y h)

So now we have two structures: a comonad w and a coalgebra:

type Coalgebra w s = s -> w s

A lens is a special case of this coalgebra where w is Store a.

Every time you have two structures, you may legitimately ask the question: Are they compatible? Just by looking at types, you may figure out some obvious compatibility conditions. In particular, since they go the opposite way, it would make sense for extract to undo the action of coalg:

coalg :: Coalgebra w s
extract . coalg = id

Also, duplicating the result of coalg should be the same as applying coalg twice (the second time lifted by fmap):

fmap coalg . coalg = duplicate . coalg

If these two conditions are satisfied, we call coalg a comonad coalgebra.

And here’s the clencher:

These two conditions when applied to the Store a comonad are equivalent to our earlier lens laws.

Let’s see how it works. First we’ll express the result of our lens coalgebra acting on some object s in terms of get and set (curried set s is a function a->s):

coalg s = Store (get s) (set s)

The first condition extract . coalg = id immediately gives us the law:

set s (get s) = s

When we act with duplicate on coalg s, we get:

Store (get s) (\y -> Store y (set s))

On the other hand, when we fmap our coalg over coalg s, we get:

Store (get s) ((\s' -> Store (get s') (set s')) . set s)

Two functions — the second components of the Store objects in those equations — must be equal when acting on any a. The first function produces:

Store a (set s)

In the second one, we first apply set s to a to get set s a, which we then pass to the lambda to get:

Store (get (set s a)) (set (set s a))

This reproduces the other two (monomorphic) lens laws:

get (set s a) = a

and

set (set s a) = set s

This algebraic construction can be extended to type-changing lenses by replacing Store with its indexed version:

data IStore a b t = IStore a (b -> t)

and the comonad with its indexed counterpart. The indexed store is also called Context in the lens parlance, and an indexed comonad is also called a parametrized comonad.

So what’s an indexed comonad? Let’s start with an indexed functor. It’s a type constructor that takes three types, a, b, and s, and is a functor in the third argument:

class IxFunctor f where
    imap :: (s -> t) -> f a b s -> f a b t

IStore is obviously an indexed functor:

instance IxFunctor IStore where
    -- imap :: (s -> t) -> IStore a b s -> IStore a b t
    imap f (IStore x h) = IStore x (f . h)

An indexed comonad has the indexed versions of extract and duplicate:

class IxComonad w where
    iextract :: w a a t -> t
    iduplicate :: w a b t -> w a j (w j b t)

Notice that iextract is “diagonal” in the index types, whereas the double application of w shares one index, j, between the two applications. This plays very well with the unit and multiplication interpretation of a monad — here it looks just like matrix multiplication (although we are dealing with a comonad rather than a monad).

It’s easy to see that the instantiation of the indexed comonad for IStore works the same way as the instantiation of the comonad for Store. The types just work out that way.

instance IxComonad IStore where
    -- iextract :: IStore a a t -> t
    iextract (IStore a h) = h a
    -- iduplicate :: IStore a b t -> IStore a c (IStore c b t)
    iduplicate (IStore a h) = IStore a (\c -> IStore c h)

There is also an indexed version of a comonad coalgebra, where the coalgebra is replaced by a family of mappings from some carrier type s to w a b t; with the type t determined by s together with the choice of of the indexes a and b:

type ICoalg w s t a b = s -> w a b t

The compatibility conditions that make it an (indexed) comonad coalgebra are almost identical to the standard compatibility conditions, except that we have to be careful about the index types. Here’s the first condition:

icoalg_aa :: ICoalg w s t a a
iextract . icoalg_aa = id

Let’s analyze the types. The inner part has the type:

icoalg_aa :: s -> w a a t

We apply iextract to it, which has the type:

iextract :: w a a t -> t

and get:

iextract . icoalg_aa :: s -> t

The right hand side of the condition has the type:

id :: s -> s

It follows that, for the diagonal components of ICoalg w s t, t must be equal to s. The diagonal part of ICoalg w s t is therefore a family of regular coalgebras.

As we have done with the monomorphic lens, we can express (ICoalg IStore s t a b), when acting on s, in terms of get and set:

icoalg_ab s = IStore (get s) (set s)

But now get s is of type a, while set s if of the type b -> t. We can still apply extract to the diagonal term IStore a a t as required by the first compatibility condition. When equating the result to id, we recover the lens law:

set s (get s) = s

Similarly, it’s straightforward to see that the second compatibility condition:

icoalg_bc :: ICoalg w s t b c
icoalg_ab :: ICoalg w s t a b
icoalg_ac :: ICoalg w s t a c
imap icoalg_bc . icoalg_ab = iduplicate . icoalg_ac

is equivalent to the other two lens laws.

The Parametric Picture

Despite being theoretically attractive, standard lenses were awkward to use and, in particular, to compose. The breakthrough came when Twan van Laarhoven realized that there is a higher-order representation for them that has very nice compositional properties. Composing lenses to focus on sub-objects of sub-objects turned into simple function composition.

Here’s Twan’s representation (generalized by Russell for the polymorphic case):

type Lens s t a b = forall f. Functor f => (a -> f b) -> (s -> f t)

So a lens is a polymorphic higher order function with a twist. The twist is that it’s polymorphic with respect to a functor rather than a type.

You can think of it this way: the caller provides a function to modify a particular field of s, turning it from type a to f b. What the caller gets back is a function that transforms the whole of s to f t. The idea is that the lens knows how to reconstruct the object, while putting it under a functor f — if you tell it how to modify a field, also under this functor.

For instance, continuing with our example, here’s the van Laarhoven lens that focuses on the first component of a pair:

vL :: Lens (a, c) (b, c) a b
vL h (x, x') = fmap (\y -> (y, x')) (h x)

Here, s is (a, c) and t is (b, c).

To see that the van Laarhoven representation is equivalent to the get/set one, let’s first change the order of arguments and pull s outside of the forall quantifier:

Lens s t a b = s -> (forall f. Functor f => (a -> f b) -> f t)

Here’s how you can read this definition: For a given s, if you give me a function from a to f b, I will produce a value of type f t. And I don’t care what functor you use!

What does it mean not to care about the functor? It means that the lens must be parametrically polymorphic in f. It can’t do case analysis on a functor. It must be implemented using the same formula for f being the list functor, or the Maybe functor, or the Const functor, etc. There’s only one thing all these functors have in common, and that’s the fmap function; so that’s what we are allowed to use in the implementation of the lens.

Now let’s think what we can do with a function a -> f b that we were given. There’s only one thing: apply it to some value of type a. So we must have access to a value of type a. The result of this application is some value of type f b, but we need to produce a value of the type f t. The only way to do it is to have a function of type b->t and sneak it under the functor using fmap (so here’s where the generic functor comes in). We conclude that the implementation of the function:

forall f. Functor f => (a -> f b) -> f t

must be hiding a value of type a and a function b->t. But that’s exactly the contents of IStore a b t. Parametricity tells us that there is an IStore hiding inside the van Laarhoven lens. The lens is equivalent to:

s -> IStore a b t

In fact, with a clever choice of functors we can recover both get and set from the van Laarhoven representation.

First we select our functor to be Const a. Note that the parameter a is not the one over which the functor is defined. Const a takes a second parameter b over which it is functorial. And, even though it takes b as a type parameter, it doesn’t use it at all. Instead, like a magician, it palms an a, and then reveals it at the end of the trick.

newtype Const a b = Const { getConst :: a }

instance Functor (Const a) where
    -- fmap :: (s -> t) -> Const a s -> Const a t
    fmap _ (Const a) = (Const a)

The constructor Const happens to be a function

Const :: a -> Const a b

which has the required form to be the first argument to the lens:

a -> f b

When we apply the lens, let’s call it vL, to the function Const, we get another function:

vL Const :: s -> Const a t

We can apply this function to s, and then, in the final reveal, retrieve the value of a that was smuggled inside Const a:

get vL s = getConst $ vL Const s

Similarly, we can recover set from the van Laarhoven lens using the Identity functor:

newtype Identity a = Identity { runIdentity :: a }

We define:

set vL s x = runIdentity $ vL (Identity . const x) s

The beauty of the van Laarhoven representation is that it composes lenses using simple function composition. A lens takes a function and returns a function. This function can, in turn, be passed as the argument to another lens, and so on.

There’s an interesting twist to this kind of composition — the function composition operator in Haskell is the dot, just like the field accessor in OO languages like Java or C++; and the composition follows the same order as the composition of accessors in those languages. This was first observed by Conal Elliott in the context of semantic editor combinators.

Consider a lens that focuses on the a field inside some object s. It’s type is:

Lens s t a b

When given a function:

h :: a -> f b

it returns a function:

h' :: s -> f t

Now consider another lens that focuses on the s field inside some even bigger object u. It’s type is:

Lens u w s t

It expects a function of the type:

g :: s -> f t

We can pass the result of the first lens directly to the second lens to form a composite:

Lens u w s t . Lens s t a b

We get a lens that focuses on the a field of the object s that is the sub-object of the big object u. It works just like in Java, where you apply a dot to the result of a getter or a setter, to dig deeper into a subobject.

Not only do lenses compose using regular function composition, but we can also use the identity function as the identity lens. So lenses form a category. It’s time to have a serious look at category theory. Warning: Heavy math ahead!

The Categorical Picture

I used parametricity arguments to justify the choice of the van Laarhoven representation for the lens. The lens function is supposed to have the same form for all functors f. Parametricity arguments have an operational feel to them, which is okay, but I feel like a solid categorical justification is more valuable than any symbol-shuffling argument. So I worked on it, and eventually came up with a derivation of the van Laarhoven representation using the Yoneda lemma. Apparently Russell O’Connor and Mauro Jaskelioff had similar feelings because they came up with the same result independently. We used the same approach, going through the Store functor and applying the Yoneda lemma twice, once in the functor category, and once in the Set category (see the Bibliography).

I would like to present the same result in a more general setting of the Yoneda embedding. It’s a direct consequence of the Yoneda lemma, and it states that any category can be embedded (fully and faithfully) in the category of functors from that category to Set.

Here’s how it works: Let’s fix some object a in some category C. For any object x in that category there is a hom-set C(a, x) of morphisms from a to x. A hom-set is a set — an object in the category Set of sets. So we have defined a mapping from C to Set that takes an x and maps it to the set C(a, x). This mapping is called C(a, _), with the underscore serving as a placeholder for the argument.

It’s easy to convince yourself that this mapping is in fact a functor from C to Set. Indeed, take any morphism f from x to y. We want to map this morphism to a function (a morphism in Set) that goes between C(a, x) and C(a, y). Let’s define this lifted function component-wise: given any element h from C(a, x) we can map it to f . h. It’s just a composition of two morphisms from C. The resulting morphism is a member of C(a, y). We have lifted a morphism f from C to Set thus establishing that C(a, _) is a functor.

Now consider two such functors, C(a, _) and C(b, _). The Yoneda embedding theorem tells us that there is a one-to-one correspondence between the set of natural transformations between these two functors and the hom-set C(b, a).

Nat(C(a, _), C(b, _)) ≅ C(b, a)

Notice the reversed order of a and b on the right-hand side.

Let’s rephrase what we have just seen. For every a in C, we can define a functor C(a, _) from C to Set. Such a functor is a member of the functor category Fun(C, Set). So we have a mapping from C to the functor category Fun(C, Set). Is this mapping a functor?

We have just seen that there is a mapping between morphisms in C and natural transformations in Fun(C, Set) — that’s the gist of the Yoneda embedding. But natural transformations are morphisms in the functor category. So we do have a functor from C to the functor category Fun(C, Set). It maps objects to objects and morphisms to morphisms. It’s a contravariant functor, because of the reversal of a and b. Moreover, it maps the hom-sets in the two categories one-to-one, so it’s a fully faithful functor, and therefore it defines an embedding of categories. Every category C can be embedded in the functor category Fun(C, Set). That’s called the Yoneda embedding.

There’s an interesting consequence of the Yoneda embedding: Every functor category can be embedded in its own functor category — just replace C with a functor category in the Yoneda embedding. Recall that functors between any two categories form a category. It’s a category in which objects are functors and morphisms are natural transformations. Yoneda embedding works for that category too, which means that a functor category can be embedded in a category of functors from that functor category to Set.

Let’s see what that means. We can fix one functor, say R and consider the hom-set from R to some arbitrary functor f. Since we are in a functor category, this hom-set is a set of natural transformations between the two functors, Nat(R, f).

Now let’s pick another functor S. It also defines a set of natural transformations Nat(S, f). We can keep picking functors and mapping them to sets (sets of natural transformations). In fact we know from the previous argument that this mapping is itself a functor. This time it’s a functor from a functor category to Set.

What does the Yoneda embedding tell us about any two such functors? That the set of natural transformations between them is isomorphic to the (reversed) hom-set. But this time hom-sets are sets of natural transformations. So we have:

Nat(Nat(R, _), Nat(S, _)) ≅ Nat(S, R)

All natural transformations in this formula are regular natural transformation except for the outer one, which is more interesting. You may recall that a natural transformation is a family of morphisms parameterized by objects. But in this case objects are functors, and morphisms are themselves natural transformations. So it’s a family of natural transformations parameterized by functors. Keep this in mind as we proceed.

To get a better feel of what’s happening, let’s translate this to Haskell. In Haskell we represent natural transformations as polymorphic functions. This makes sense, since a natural transformation is a family of morphisms (here functions) parameterized by objects (here types). So a member of Nat(R, f) can be represented as:

forall x. R x -> f x

Similarly, the second natural transformation in our formula turns into:

forall y. S y -> f y

As I said, the outer natural transformation in the Yoneda embedding is a family of natural transformations parameterized by a functor, so we get:

forall f. Functor f => (forall x. R x -> f x) -> (forall y. S y -> f y)

You can already see one element of the van Laarhoven representation: the quantification over a functor.

The right hand side of the Yoneda embedding is a natural transformation:

forall z. S z -> R z

The next step is to pick the appropriate functors for R and S. We’ll take R to be IStore a b and S to be IStore s t.

Let’s work on the first part:

forall x. IStore a b x -> f x

A function from IStore a b x is equivalent to a function of two arguments, one of them of type a and another of type b->x:

forall x. a -> (b -> x) -> f x

We can pull a out of forall to get:

a -> (forall x. (b -> x) -> f x)

If you squint a little, you recognize that the thing in parentheses is a natural transformation between the functor C(b, _) and f, where C is the category of Haskell types. We can now apply the Yoneda lemma, which says that this set of natural transformations is isomorphic to the set f b:

forall x. (b -> x) -> f x ≅ f b

We can apply the same transformation to the second part of our identity:

forall y. (IStore s t y -> f y) ≅ s -> f t

Taking it all together, we get:

forall f. Functor f => (a -> f b) -> (s -> f t) 
    ≅ forall z. IStore s t z -> IStore a b z

Let’s now work on the right hand side:

forall z. IStore s t z -> IStore a b z 
    ≅ forall z. s -> (t -> z) -> IStore a b z

Again, pulling s out of forall and applying the Yoneda lemma, we get:

s -> IStore a b t

But that’s just the standard representation of the lens:

s -> IStore a b t ≅ (s -> a, s -> b -> t) = (get, set)

Thus the Yoneda embedding of the functor category leads to the van Laarhoven representation of the lens:

forall f. Functor f => (a -> f b) -> (s -> ft) 
  ≅ (s -> a, s -> b -> t)

Playing with Adjunctions

This is all very satisfying, but you may wonder what’s so special about the IStore functor? The crucial step in the derivation of the van Laarhoven representation was the application of the Yoneda lemma to get this identity:

forall x. IStore a b x -> f x ≅ a -> f b

Let’s rewrite it in the more categorical language:

Nat(IStore a b, f) ≅ C(a, f b)

The set of natural transformations from the functor IStore a b to the functor f is isomorphic to the hom-set between a and f b. Any time you see an isomorphism of hom-sets (and remember that Nat is the hom-set in the functor category), you should be on the lookout for an adjunction. And indeed, we have an adjunction between two functors. One functor is defined as:

a -> IStore a b

It takes an object a in C and maps it to a functor IStore a b parameterized by some other object b. The other functor is:

f -> f b

It maps a functor, an object in the functor category, to an object in C. This functor is also parameterized by the same b. Since this is a flipped application, I’ll call it Flapp:

newtype Flapp b f = Flapp (f b)

So, for any b, the functor-valued functor IStore _ b is left adjoint to Flapp b. This is what makes IStore special.

As a side note: IStore a b is a covariant functor in a and a contravariant functor in b. However, Store a is not functorial in a, because a appears in both positive and negative position in its definition. So the adjunction trick doesn’t work for a simple (monomorphic) lens.

We can now turn the tables and use the adjunction to define the functor IStore in an arbitrary category (notice that the Yoneda lemma worked only for Set-valued functors). We just define a functor-valued functor IStore to be the left adjoint to Flapp, provided it exists.

Nat(IStore a b, f) ≅ C(a, f b)

Here, Nat is a set of natural transformations between endofunctors in C.

We can substitute the so defined functor into the Yoneda embedding formula we used earlier:

Nat((Nat(IStore a b, f), Nat(IStore s t, f)) 
    ≅ Nat(IStore s t, IStore a b)

We can now use the adjunction, rather than the Yoneda lemma, to eliminate some of the occurrences IStore:

Nat(C(a, f b), C(s, f t))
    ≅ C(s, IStore a b t)

This is slightly more general than the original van Laarhoven equivalence.

We can go even farther and reproduce the Jaskelioff and O’Connor trick of constraining the generic functor in the definition of the van Laarhoven lens to a pointed or applicative functor. This results in a multi-focus lens. In particular, if we use pointed functors, we get lenses with zero or one targets, so called affine lenses. Restricting the functors further to applicative leads to lenses with any number of targets, or traversals.

The trick is that any pointed or applicative functor can be stripped of the additional functionality and treated just like any other functor. This act of “forgetting” about pure and <*> may itself be considered a functor in the functor category. It’s called, appropriately, a forgetful functor. The left adjoint to a forgetful functor (if it exists) is called a free functor. It takes an arbitrary functor and creates a pointed functor by generating an artificial pure; or it creates an applicative functor by adding <*>. This adjunction is described by a natural isomorphism of hom-sets — in this case sets of natural transformations:

Nat(S, U f) ≅ Nat(S*, f)

Here, U is the forgetful functor, and S* is the free applicative/pointed version of the functor S. The functor f ranges across applicative (respectively, pointed) functors.

Now we can try to substitute the free version of IStore in the Yoneda embedding formula:

Nat((Nat(IStore* a b, f), Nat(IStore* s t, f)) 
    ≅ Nat(IStore* s t, IStore* a b)

The formula holds for any applicative (pointed) functor f and a set of natural transformations over such functors.

The first step is to use the forgetful/free adjunction:

Nat((Nat(IStore a b, U f), Nat(IStore s t, U f)) 
    ≅ Nat(IStore s t, U IStore* a b)

Then we can use our defining adjunction for IStore to get:

Nat(C(a, U f b), C(s, U f t)) 
    ≅ C(s, U IStore* a b t)

In Haskell notation this reads:

forall f. Applicative f => (a -> f b) -> (s -> f t)
    ≅ s -> IAppStore a b t

(the action of U is implicit).

The free applicative version of IStore is defined as:

data IAppStore a b t = 
    Unit t
  | IAppStore a (IAppStore a b (b -> t))

These are all known results, but the use of the Yoneda embedding and the adjunction to define the IStore functor makes the derivation more compact and slightly more general.

Acknowledgments

I’m grateful to Mauro Jaskelioff, Gershom Bazerman, and Joseph Abrahamson for reading the draft and providing helpful comments and to André van Meulebrouck for editing help.

Bibliography

1. Edward Kmett, The Haskell Lens Library
2. Simon Peyton Jones, Lenses: Compositional Data Access and Manipulation. A Skills Matter video presentation.
3. Joseph Abrahamson, A Little Lens Starter Tutorial
4. Joseph Abrahamson, Lenses from Scratch
5. Artyom, lens over tea tutorial
6. Twan van Laarhoven, CPS based functional references
7. Bartosz Milewski, Lenses, Stores, and Yoneda
8. Mauro Jaskelioff, Russell O’Connor, A Representation Theorem for Second-Order Functionals
9. Bartosz Milewski, Understanding Yoneda