“You must be kidding!” would be the expected reaction to “Monads in C++.” Hence my surprise when I was invited to Boostcon 11 to give a three-hour presentation on said topic, a presentation which was met with totally unexpected level of interest. I imagine there was a small uptick in the sales of Haskell books afterwards.
Before I answer the question: “Why are monads relevant in C++?”, let me first answer the question: “Why is Haskell relevant in C++?” It turns out that Haskell makes C++ template metaprogramming if not easy then at least approachable (see my blog, What Does Haskell Have to Do with C++?). You have to understand that compile-time C++ is a strict functional language operating (mostly) on types. If that is not immediately obvious, it’s because the C++ template syntax is so appalling.
Now, not everybody falls in love with the Haskell syntax (at least not at first sight) but it fits the functional paradigm much better than anything else. What’s more, the correspondence between Haskell code and C++ template code is so direct that it could almost be translated mechanically. It really pays to design and test your template metaprograms in Haskell first, before translating them to C++. Conversely, translating complex template code to Haskell may help you understand it better and enable you to maintain and extend it. Those were my reasons to advocate the use of Haskell as a pseudo-language for C++ template metaprogramming.
Armed with Haskell I could study and analyze some of the most sophisticated C++ metacode. But when I looked at Eric Niebler’s Boost Proto library and couldn’t make heads or tails of it, even after discussing it with him over email and over beers, I was stumped.
Monads and EDSLs
Boost Proto is a library for implementing domain-specific languages (DSLs). It’s an impressive piece of C++ metaprogramming but it’s hard to comprehend and it doesn’t yield to straightforward translation to Haskell. The problem is that it combines compile-time constructs with run time code in a non-trivial way. I struggled long with Proto until one day I had an epiphany– I was looking at a monad. But first:
What Is an EDSL?
Great things come out of abusing C++. One example is the abuse of templates (which were originally designed to support parametrized data types) to express compile-time computations. The result is Template Metaprogrammming (TMP). Another example is the abuse of operator overloading, which created a fertile ground for Embedded Domain-Specific Languages (EDSLs). Eric’s Proto combined the two abominations into a library for constructing EDSLs.
In this post I will construct a simple EDSL in C++. This is how it works:
- You overload the heck out of operators
- The overloaded operators build trees from expressions instead of eagerly computing results
- The type of the tree encodes the structure of the expression that created it. Since it’s a type, the structure of the expression is available at compile time
- You construct an object of that type
- You execute that object (because it is a function object) with appropriate arguments, and get the results you wanted.
A more general EDSL will also create a runtime data structure that stores the values of any variables and literals in the expression. Algorithms can walk the tree at compile time, runtime, or both to compute values and perform actions. You can even write a compile time algorithm to compute a runtime algorithm that munges trees in interesting ways.
My moment of Zen was when I realized that an EDSL corresponds to a Haskell reader monad. (If you’re not familiar with Haskell or monads, read my series, Monads for the Curios Programmer.) To my own amazement this analogy worked and led to executable code.
| Haskell Monad |
C++ “Monad” |
| Composition of monadic functions |
Compile-time parsing of expressions |
| Execution of compound action on astate |
Application of function object to runtime values |
To prove the concept, I picked a simple EDSL based on one of the Eric’s examples. It’s a two-argument lambda EDSL. It lets you write an expression with two placeholders, arg1 and arg2. Through the magic of templates and operator overloading, this expression is interpreted as an anonymous function of two arguments. Here’s an example which evaluates to 25:
int x = (arg1 * arg2 + 13)(3, 4)
It turns out that the most important step in this process is to be able to convert an expression tree into a function object. Let me do this in Haskell first, and then translate it into C++.
The Expression Monad in Haskell
Let’s start with a short:
Reader Monad Refresher
A reader monad (a state monad with immutable state) provides a way to express stateful computations in a pure functional language. A stateful computation takes some arguments and returns a value, but unlike a function, it makes use of some external state. This computation can be turned into a function that takes the same arguments but, instead of returning a value, returns another function that takes a state as an argument and calculates the value. (The distinction between a computation and a function is essential here.)

Statefull computation represented as a monadic function returning an action
State
The state, in the case of our expression monad, is a collection of two values — the arguments to the lambda. They will be used to replace the two placeholders in the expression.
Here’s the definition of our state — a list of integers (we really need only two, but I’m being sloppy… I mean general):
type Args = [Int]
Actions
An action is a function that takes the state and produces a value of arbitrary type t:
Args -> t
You might remember from my previous post that one element of the monad is a type constructor: a mapping of an arbitrary type into an enriched type. In this case the enriched type is an action type. Because of technicalities related to Haskell’s type inference, I’ll have to thinly encapsulate an action inside a new type, which I will call Prog:
newtype Prog t = PR (Args -> t)
The idea is that the composition of monadic actions is similar to the compilation of source code: it produces a “program,” which is then “run.” In fact, I’ll define an auxiliary function that does just that, it runs a “program”:
run :: Prog t -> Args -> t
run (PR act) args = act args
This is a function that takes a Prog t as its first argument and pattern matches it to the constructor (PR act). The second argument is the state, args of type Args. The result of running the program is a value of type t.
Monadic Functions
The next step is to define some primitive monadic functions. These are functions that produce actions (or “programs”). Here’s a very useful function that produces an action that extracts the n’th value from the list of arguments (the state):
getArg :: Int -> Prog Int
getArg n = PR (λ args -> args !! n)
getArg takes an Int (in our case, zero or one) and returns a lambda (encapsulated in a Prog using the constructor PR). This lambda takes a list of Ints, args, and extracts its n’th element (args !! n means: take the n’th element of the list, args).
You’ve seen examples of monadic functions in my previous blog post, but it’s worth repeating the idea: getArg is a function that returns an action that is like a promise to extract the n’th argument when the arguments become available.
Just for fun, here’s another monadic function that takes n and promises to return twice n when the arguments are provided. It doesn’t matter that the arguments are going to be ignored.
doubleIt n = PR (λ args -> 2 * n)
Monadic Bind
I need two monadic functions, getArg and doubleIt, in order to demonstrate their composition using “bind.” I want to create an action that will get the first argument using getArg 0 and double it using doubleIt v. If you remember how “bind” works, it takes an action, in this case the result of getArg 0, and a continuation, which represents “the rest of the computation.”
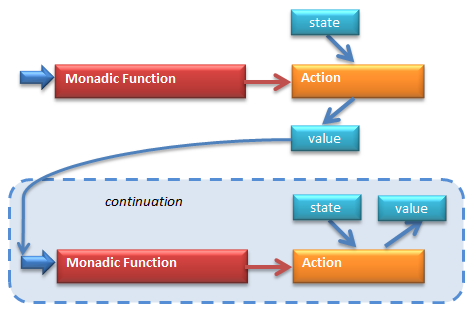
Combining two monadic functions using bind
In our case, the continuation is a lambda that takes an argument v (that’s the future result of the first action) and performs doubleIt v.
λ v -> doubleIt v
This lambda returns an action because doubleIt v returns an action.
The signature of bind is:
bind :: (Prog a) -> (a -> (Prog b)) -> (Prog b)
You might have noticed that I use the words “action” and “program” interchangeably, although, strictly speaking, an action is the contents of a program. However, this distinction is an artifact or a Haskell quirk — a monad can’t be defined using a type alias, so we need the Prog type to encapsulate the action. Curiously, we won’t have this problem in C++.
The purpose of bind is to glue together an action with a continuation and return a new action. That means that bind has to return a lambda of appropriate type:
bind (PR act) cont =
PR (λ args -> ... produce value of type b ...)
This lambda will be executed when arguments are available. At that point, with the arguments handy, we’ll be able to first execute the action, act, and pass its result to the continuation. The continuation will return another action, which we can promptly execute too:
bind (PR act) cont =
PR (λ args ->
let v = act args
(PR act') = cont v
in
act' args)
(In Haskell you can use primed variables, like act'. I like that notation.)
This is very much like the state monad bind, except that we don’t have to worry about chaining the state, which is immutable. In fact the above is the definition of the reader monad’s bind.
Let’s test our new bind by composing getArg with doubleIt:
test0 :: Prog Int
test0 =
bind (getArg 0) (λ v -> doubleIt v)

Composing monadic function, GetArg, with the continuation that calls another monadic function, doubleIt
We can run the program produced by test0 to see that it actually works:
> let prog = test0
> run prog [3,4]
6
> run prog [11,0]
22
For completeness, here’s the full definition of the Prog reader monad:
instance Monad Prog where
return v = PR (λ args -> v)
(PR act) >>= cont = PR (λ arg -> let v = act arg
(PR act') = cont v
in act' arg)
With that definition, we can rewrite our little example in the do notation:
test1 = do
v <- getArg 0
doubleIt v
Expression Tree
We have the definition of a program — a thinly encapsulated action. To create an actual program we need some kind of source code and a compiler. Our source code takes the form of an expression tree. A tree in Haskell is defined as a tagged union:
data Exp = Const Int
| Plus Exp Exp
| Times Exp Exp
| Arg1
| Arg2
The first constructor, Const takes an Int and creates a leaf node corresponding to this constant value. The next two constructors are recursive, they each take two expressions and produce, correspondingly, a Plus and a Times node. Finally, there are two placeholders for the two arguments that will be provided at “runtime.”
Compilation
Compilation is turning source code into a program. This process can be represented as a function with the following signature:
compile :: Exp -> Prog Int
It takes an expression tree (the source) and returns a program that evaluates to an integer. Looking from another perspective, compile is just a monadic function in our Prog monad.
We will define compile in little steps driven by the various patterns in the definition of Exp. If the expression matches the Const node, we define compile as:
compile (Const c) = return c
Remember, return is a function that takes a value and returns an action (program) that will produce this value when executed.
Another easy case is Arg1 (and Arg2)–we already have a monadic function getArg that we can call:
compile Arg1 = getArg 0
The interesting case is the Plus (or Times) node. Here we have to recursively call compile for both children and then compose the results. Well, that’s what monadic function composition is for. Here’s the code using the do notation, hiding the calls to bind:
compile (Plus e1 e2) =
do
v1 <- compile e1
v2 <- compile e2
return (v1 + v2)
That’s it! We can now compile a little test expression (Arg1 * Arg2 + 13):
testExp =
let exp = (Plus (Times Arg1 Arg2)(Const 13))
in compile exp
and we can run the resulting program with an argument list:
> let args = [3, 4]
> let prog = testExp
> run prog args
25
The Expression Monad in C++
The translation of the Haskell expression monad to C++ is almost embarrassingly easy. I’ll be showing Haskell code side by side with its C++ equivalents.
Expression Tree
data Exp = Const Int
| Plus Exp Exp
| Times Exp Exp
| Arg1
| Arg2
In C++, the expression tree is a compile-time construct that is expressed as a type (I’ll show you later where this type originates from). We have separate types for all the leaves, and the non-leaf nodes are parametrized by the types of their children.
template<int n> struct Const {};
template<class E1, class E2>
struct Plus {};
template<class E1, class E2>
struct Times {};
struct Arg1 {};
struct Arg2 {};
For instance, here’s the type that corresponds to the expression arg1*arg2+13:
Plus<Times<Arg1, Arg2>, Const<13>>
State
Haskell:
type Args = [Int]
C++: State is a runtime object. I implemented it using an array of two integers and, for good measure, I added a constructor and an accessor.
struct Args
{
Args(int i, int j) {
_a[0] = i;
_a[1] = j;
}
int operator[](int n) { return _a[n]; }
int _a[2];
};
Action
Here’s the tricky part: How to represent an action? Remember, an action takes state, which is now represented by Args, and returns a value of some type. Because Args are only available at runtime, an action must be a runtime function or, even better, a function object.
How does that fit in our compile-time/runtime picture? We want our C++ monadic functions to be “executed” at compile time, but they should produce actions that are executed at runtime. All we can do at compile time is to operate on types, and this is exactly what we’ll do. We will create a new type that is a function object. A function object is a struct that implements an overloading of a function-call operator.
There’s another way of looking at it by extending the notion of a metafunction. In one of my previous posts I described metafunctions that “return” values, types, or even other metafunctions. Here we have a metafunction that returns a (runtime) function. This view fits better the Haskell monadic picture where a monadic function returns an action.
Type Constructor
Unfortunately, not everything can be expressed as neatly in C++ as it is in Haskell. In particular our type constructor:
newtype Prog t = PR (Args -> t)
doesn’t have a direct C++ counterpart. It should be a template that, for any type T, defines an action returning that type. In this construction, an action is represented by a C++ function object, so we would like something like this:
template<class T> struct PR {
T operator()(Args args);
};
which, for many reasons, is useless. What we really need is for PR to be a “concept” that specifies a type with an associated method, operator(), of a particular signature. Since concepts are not part of C++11, we’ll have to rely on programming discipline and hope that, if we make a mistake, the compiler error messages will not be totally horrible.
Monadic Metafunction
Let’s start by translating the Haskell monadic function getArg:
getArg :: Int -> Prog Int
getArg n = PR (λ args -> args !! n)
Here it is in C++:
template<int n>
struct GetArg { // instance of the concept PR
int operator()(Args args) {
return args[n];
}
};
It is a metafunction that takes a compile-time argument n and “returns” an action. Translation: it defines a struct with an overloaded operator() that takes Args and returns an int. Again, ideally this metafunction should be a struct that is constrained by the concept PR.
Bind
Let’s look again at the Haskell’s implementation of monadic bind:
bind (PR prog) cont =
PR (λ args ->
let v = prog args
(PR prog') = cont v
in
prog' args)
It takes two arguments: an action and a continuation. We know what an action is in our C++ construction: it’s a function object with a particular signature. We’ll parameterize our C++ Bind with the type, P1, of that object. The continuation is supposed to take whatever that action returns and return a new action. The type of that new action, P2, will be the second template parameter of Bind.
We’ll encode the type of the continuation as the standard function object taking an int and returning P2:
std::function<P2(int)>
Now, the C++ Bind is a metafunction of P1 and P2 that “returns” an action. The act of “returning” an action translates into defining a struct with the appropriate overload of operator(). Here’s the skeleton of this struct:
template<class P1, class P2> // compile-time type parameters
struct Bind {
Bind(P1 prog, std::function<P2(int)> cont)
: _prog(prog), _cont(cont)
{}
...
P1 _prog;
std::function<P2(int)> _cont;
};
Notice that at runtime we will want to construct an object of this type, Bind, and pass it the runtime arguments: the action and the continuation. The role of the constructor requires some explanation. Haskell function bind is a monadic function of two arguments. Its C++ counterpart is a metafunction that takes four arguments: P1 and P2 at compile time, and prog and cont at runtime. This is a general pattern: When constructing a monadic metafunction in C++ we try to push as much as possible into compile time, but some of the arguments might not be available until runtime. In that case we shove them into the constructor.
The interesting part is, of course, the function-call operator, which really looks like a one-to-one translation of the Haskell implementation:
template<class P1, class P2>
struct Bind {
...
int operator()(Args args) {
int v = _prog(args);
P2 prog2 = _cont(v);
return prog2(args);
}
...
};
Things to observe: A smart compiler should be able to inline all these calls because it knows the types P1 and P2, so it can look up the implementations of their function-call operators. What’s left to the runtime is just the operations on the actual runtime values, like the ones done inside GetArg::operator(). However, I have been informed by Eric Niebler that many of these optimizations are thwarted by the choice of std::function for the representation of the continuation. This problem can be overcome, but at some loss of clarity of code, so I’ll stick to my original implementation (also, see Appendix 2).
Return
All that is left to complete the monad is the return function. Here it is in Haskell:
return :: a -> Prog a
return v = PR (λ args -> v)
And here it is, as a function object, in C++:
struct Return
{
Return(int v) : _v(v) {}
int operator()(Args args)
{
return _v;
}
int _v;
};
Of course, in full generality, Return should be parameterized by the return type of its operator(), but for this example a simple int will do. The argument v is only available at runtime, so it is passed to the constructor of Return.
The “Compile” Metafunction in C++
Now that we have our monad implemented, we can use it to build complex monadic functions from simple ones (such as GetArg). In Haskell we have implemented a monadic function compile with the following signature:
compile :: Exp -> Prog Int
It takes an expression tree and returns an action that evaluates this tree.
The C++ equivalent is a metafunction that takes a (compile-time) expression tree and defines a struct with the appropriate overload of a function-call operator. Lacking concept support, the latter requirement can’t be directly expressed in C++. We can, and in fact have to, provide a forward declaration of Compile:
template<class Exp>
struct Compile;
In Haskell, we defined compile using pattern matching. We can do the same in C++. Just like we split the Haskel definition of compile into multiple sub-definitions corresponding to different argument patterns, we’ll split the C++ definition into multiple specializations of the general template, Compile.
Here’s the first specialization in Haskell:
compile (Const c) = return c
and in C++:
template<int c>
struct Compile<Const<c>> : Return
{
Compile() : Return(c) {}
};
I could have defined a separate overload of operator() for this case, but it’s simpler to reuse the one in Return.
Here’s another trivial case:
compile Arg1 = getArg 0
translates into:
template<>
struct Compile<Arg1> : GetArg<0> {};
The real fun begins with the Plus node, because it involves composition of monadic functions. Here’s the de-sugared Haskell version:
compile (Plus exL exR) =
bind compile exL
λ left ->
bind compile exR
λ right ->
return (left + right)
The logic is simple: First we compile the left child and bind the result with the continuation (the lambda) that does the rest. Inside this continuation, we compile the right child and bind the result with the continuation that does the rest. Inside that continuation we add the two results (they are the arguments to the continuation) and encapsulate the sum in an action using return.
In C++, the binding is done by creating the appropriate Bind object and passing it (in the constructor) a function object and a continuation. The function object is the result of the compilation of the left child (we construct a temporary object of this type on the fly):
Compile<L>()
Just like in Haskell, the continuation is a lambda, only now it’s the C++11 lambda. Here’s the code, still with some holes to be filled later:
template<class L, class R>
struct Compile<Plus<L, R>> {
int operator()(Args args)
{
return Bind<...> (
Compile<L>(),
[](int left) {
return Bind<...>(
Compile<R>(),
[left](int right) {
return Return(left + right);
}
);
}
)(args);
}
};
Notice that the second lambda must explicitly capture the local variable, left. In Haskell, this capture was implicit.
The types for the instantiations of the two Bind templates can be easily derived bottom up. Ideally, we would like the compiler to infer them, just like in Haskell, but the C++ compiler is not powerful enough (although, at the cost of muddying the code some more, one can define template functions that return Bind objects of appropriate types — in C++ type inference works for template functions).
Here’s the final implementation with the types filled in:
template<class L, class R>
struct Compile<Plus<L, R>> {
int operator()(Args args)
{
return Bind<Compile<L>, Bind<Compile<R>, Return>> (
Compile<L>(),
[](int left) -> Bind<Compile<R>, Return> {
return Bind<Compile<R>, Return>(
Compile<R>(),
[left](int right) -> Return {
return Return(left + right);
}
);
}
)(args);
}
};
It’s quite a handful and, frankly speaking, I would have never been able to understand it, much less write it, if it weren’t for Haskell.
The Test
You can imagine the emotional moment when I finally ran the test and it produced the correct result. I evaluated the simple expression, Arg1*Arg2+13, with arguments 3 and 4 and got back 25. The monad worked!
void main () {
Args args(3, 4);
Compile<Plus<Times<Arg1, Arg2>, Const<13>>> act;
int v = act(args);
std::cout << v << std::endl;
}
The EDSL
Now that we have the monad and a monadic function Compile, we can finally build a simple embedded domain-specific language. Our minimalistic goal is to be able to evaluate the following expression:
int x = (arg1 + arg2 * arg2)(3, 4);
The trick is to convince the compiler to construct a very special type that represents the particular expression tree. In our case it should be something like this:
Plus< Arg1, Times<Arg2, Arg2> >
With this type, call it E, the compiler should call a special metafunction we’ll call Lambda, which returns a function object of two integral arguments:
template<class E>
struct Lambda {
int operator()(int x, int y) {
Args args(x, y);
Compile<E> prog;
return prog(args);
}
};
How does one do it? This is really the bread and butter of EDSL writers — pretty elementary stuff — but I’ll explain it anyway. We start by declaring two objects, arg1 and arg2:
const Lambda<Arg1> arg1;
const Lambda<Arg2> arg2;
These little objects can infect any expression with their Lambda-ness, and spread the infection with the help of appropriately overloaded arithmetic operators.
For instance, when the compiler sees arg1+arg2, it will look for the overload of operator+ that takes two Lambdas. And we’ll provide this one:
template<class E1, class E2>
Lambda<Plus<E1, E2>> operator+ (Lambda<E1> e1, Lambda<E2> e2)
{
return Lambda<Plus<E1, E2>>();
}
Notice that this operator returns another Lambda, albeit of a more complex type, thus spreading the Lambda-ness even further, and so on. (In this very simplified example I’m ignoring the arguments e1 and e1. In general they would be used to create a runtime version of the expression tree.)
Let’s see how it works in our example:
(arg1 + arg2 * arg2)(3, 4)
The seed types are, respectively,
Lambda<Arg1>, Lambda<Arg2>, Lambda<Arg2>
The application of the inner operator* (its definition is left as an exercise to the reader), produces the following type:
Lambda<Times<Arg2, Arg2>>
This type is passed, along with Lambda<Arg1> to operator+, which returns:
Lambda<Plus<Arg1, Times<Arg2, Arg2>>
All this is just type analysis done by the compiler to find out what type of object is returned by the outermost call to operator+.
The next question the compiler asks itself is whether this object can be called like a function, with the two integer arguments. Why, yes! A Lambda object (see above) defines an overload of the function-call operator. The instantiation of this particular Lambda defines the following overload:
int Lambda<Plus<Arg1, Times<Arg2, Arg2>>::operator()(int x, int y) {
Args args(x, y);
Compile<Plus<Arg1, Times<Arg2, Arg2>> prog;
return prog(args);
}
This function will be called at runtime with the arguments 3 and 4 to produce the expected result, 19.
The code that has to be actually executed at runtime is the call to prog(args), which is mostly a series of Binds, an addition, and a multiplication. Since the implementation of a Bind‘s function-call operators has no flow of control statements (if statements or loops), it can all be inlined by an optimizing compiler (modulo the glitch with std::function I mentioned earlier). So all that’s left is the addition and multiplication. Eric tells me that this is how Proto expressions work, and there is no reason why the monadic version wouldn’t lead to the same kind of performance.
Conculsions and Future Work
I came up with this C++ monadic construction to help me understand the kind of heavy-duty template metaprogramming that goes on in Proto. Whether I have succeeded is a matter of opinion. I exchanged some of the complexity of template manipulations for a different complexity of Haskell and monads. I would argue that any C++ template metaprogrammer should know at least one functional language, so learning Haskell is a good investment. Monads are just part of the same Haskell package.
Assuming you understand monads, is the monadic construction of an EDSL simpler than the original using Proto? I will argue that it is. The implementation of Proto is pretty much monolithic, the concepts it’s using have very little application or meaning outside of Proto. The monadic approach, on the other hand, decomposes into several layers of abstraction. At the bottom you have the construction of the state-, or reader-, monad. The monad exposes just three primitives: the type constructor, bind, and return. With these primitives you can create and compose monadic (meta-) functions — in my example it was the compile metafunction. Finally, you use these metafunctions to build an EDSL.
With this three-layer structure comes a well defined set of customization points. Users may plug in their own type constructors and implement their own Bind and Return. Or, they might use the default monad and just create their own monadic functions. It’s important that the procedure for building and composing monadic functions is well defined and that it uses straight C++ for implementing the logic. Inside a monadic function you can use regular C++ statements and standard control flow devices.
It’s not yet totally clear how general this approach is — after all what I described is a toy example. But there is a lot of interest in re-thinking or maybe even re-implementing Boost Proto and Phoenix in terms of monads. At Boostcon I started working with Joel Falcou and Hartmut Kaiser on this project, and later Eric Niebler and Thomas Heller joined our group. We believe that having solid theoretical foundations might encourage wider acceptance of some of the more complex template libraries. Especially if strict one-to-one correspondence with Haskell code could be established.
Acknowledgments
I’ve been given so much feedback on my Boostcon presentation and the drafts of this blog post that I should really list the following people as co-authors: Eric Niebler, Thomas Heller, Joel Falcou, and Hartmut Keiser. Thank you guys!
This page has been translated into Spanish language by Maria Ramos.
Appendix 1
The picture wouldn’t be complete if I didn’t provide the translation of the EDSL construction back to Haskell. It’s pretty straightforward, except for the last part where an expression becomes a callable function object. Maybe there is a way to bend Haskell’s syntax to do it directly but, since this is just a proof of concept, I took a shortcut and defined a function toFun which turns a Lambda expression into a function.
newtype Lambda = L Exp
toFun (L ex) =
λ x y ->
run (compile ex) [x, y]
instance Num Lambda where
(L e1) + (L e2) = L (Plus e1 e2)
(L e1) * (L e2) = L (Times e1 e2)
fromInteger n = L (Const (fromInteger n))
test =
let arg1 = L Arg1
arg2 = L Arg2
in
(toFun (arg1 + 2 * arg2 * arg2)) 2 3
The overloading of arithmetic operators is done by making Lambda an instance of the type class Num.
Appendix 2
When writing code at this level of abstraction it’s easy to bump into compiler bugs. For instance, Visual Studio 2010 won’t instantiate this simpler version of Bind that doesn’t use std::function:
template<class P1, class Cont>
struct Bind
{
Bind(P1 prog, Cont f)
: _prog(prog), _f(f)
{}
int operator()(State args) {
int v = _prog(args);
auto p2 = _f(v);
return p2(args);
}
P1 _prog;
Cont _f; // store a lambda continuation
};
Bibliography
- Bartosz Milewski, Monads for the Curious Programmer:
- Bartosz Milewski, What Does Haskell Have to Do with C++?
- Eric Niebler, Expressive C++. A series of blog posts that started all this
- Brian McNamara and Yannis Smaragdakis, Functional Programming in C++. A Haskell-in-C++ library
- Brian McNamara and Yannis Smaragdakis, Syntax sugar for C++: lambda, infix, monads, and more. More traditional approach to monads in C++ as a runtime device
- Zoltán Porkoláb, Ábel Sinkovics, Domain-specific Language Integration with Compile-time Parser Generator Library. A C++ implementation of a compile-time parser that uses a monadic approach (although the word “monad” is never mentioned in the paper)