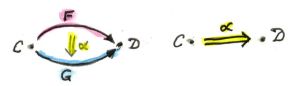April | 2015 | Bartosz Milewski's Programming Cafe

April 2015

Monthly Archive

April 15, 2015

Category Theory and Declarative Programming

Posted by Bartosz Milewski under Category Theory
[19] Comments

This is part 11 of Categories for Programmers. Previously: Natural Transformations. See the Table of Contents.

Introduction to Part II

In the first part of the book I argued that both category theory and programming are about composability. In programming, you keep decomposing a problem until you reach the level of detail that you can deal with, solve each subproblem in turn, and re-compose the solutions bottom-up. There are, roughly speaking, two ways of doing it: by telling the computer what to do, or by telling it how to do it. One is called declarative and the other imperative.

You can see this even at the most basic level. Composition itself may be defined declaratively; as in, h is a composite of g after f:

h = g . f

or imperatively; as in, call f first, remember the result of that call, then call g with the result:

h x = let y = f x
      in g y

The imperative version of a program is usually described as a sequence of actions ordered in time. In particular, the call to g cannot happen before the execution of f completes. At least, that’s the conceptual picture — in a lazy language, with call-by-need argument passing, the actual execution may proceed differently.

In fact, depending on the cleverness of the compiler, there may be little or no difference between how declarative and imperative code is executed. But the two methodologies differ, sometimes drastically, in the way we approach problem solving and in the maintainability and testability of the resulting code.

The main question is: when faced with a problem, do we always have the choice between a declarative and imperative approaches to solving it? And, if there is a declarative solution, can it always be translated into computer code? The answer to this question is far from obvious and, if we could find it, we would probably revolutionize our understanding of the universe.

Let me elaborate. There is a similar duality in physics, which either points at some deep underlying principle, or tells us something about how our minds work. Richard Feynman mentions this duality as an inspiration in his own work on quantum electrodynamics.

There are two forms of expressing most laws of physics. One uses local, or infinitesimal, considerations. We look at the state of a system around a small neighborhood, and predict how it will evolve within the next instant of time. This is usually expressed using differential equations that have to be integrated, or summed up, over a period of time.

Notice how this approach resembles imperative thinking: we reach the final solution by following a sequence of small steps, each depending on the result of the previous one. In fact, computer simulations of physical systems are routinely implemented by turning differential equations into difference equations and iterating them. This is how spaceships are animated in the asteroids game. At each time step, the position of a spaceship is changed by adding a small increment, which is calculated by multiplying its velocity by the time delta. The velocity, in turn, is changed by a small increment proportional to acceleration, which is given by force divided by mass.

These are the direct encodings of the differential equations corresponding to Newton’s laws of motion:

F = m dv/dt
v = dx/dt

Similar methods may be applied to more complex problems, like the propagation of electromagnetic fields using Maxwell’s equations, or even the behavior of quarks and gluons inside a proton using lattice QCD (quantum chromodynamics).

This local thinking combined with discretization of space and time that is encouraged by the use of digital computers found its extreme expression in the heroic attempt by Stephen Wolfram to reduce the complexity of the whole universe to a system of cellular automata.

The other approach is global. We look at the initial and the final state of the system, and calculate a trajectory that connects them by minimizing a certain functional. The simplest example is the Fermat’s principle of least time. It states that light rays propagate along paths that minimize their flight time. In particular, in the absence of reflecting or refracting objects, a light ray from point A to point B will take the shortest path, which is a straight line. But light propagates slower in dense (transparent) materials, like water or glass. So if you pick the starting point in the air, and the ending point under water, it’s more advantageous for light to travel longer in the air and then take a shortcut through water. The path of minimum time makes the ray refract at the boundary of air and water, resulting in Snell’s law of refraction:

sin θ₁ / sin θ₂ =  v₁ / v₂

where v₁ is the speed of light in the air and v₂ is the speed of light in the water.

All of classical mechanics can be derived from the principle of least action. The action can be calculated for any trajectory by integrating the Lagrangian, which is the difference between kinetic and potential energy (notice: it’s the difference, not the sum — the sum would be the total energy). When you fire a mortar to hit a given target, the projectile will first go up, where the potential energy due to gravity is higher, and spend some time there racking up negative contribution to the action. It will also slow down at the top of the parabola, to minimize kinetic energy. Then it will speed up to go quickly through the area of low potential energy.

Feynman’s greatest contribution was to realize that the principle of least action can be generalized to quantum mechanics. There, again, the problem is formulated in terms of initial state and final state. The Feynman path integral between those states is used to calculate the probability of transition.

The point is that there is a curious unexplained duality in the way we can describe the laws of physics. We can use the local picture, in which things happen sequentially and in small increments. Or we can use the global picture, where we declare the initial and final conditions, and everything in between just follows.

The global approach can be also used in programming, for instance when implementing ray tracing. We declare the position of the eye and the positions of light sources, and figure out the paths that the light rays may take to connect them. We don’t explicitly minimize the time of flight for each ray, but we do use Snell’s law and the geometry of reflection to the same effect.

The biggest difference between the local and the global approach is in their treatment of space and, more importantly, time. The local approach embraces the immediate gratification of here and now, whereas the global approach takes a long-term static view, as if the future had been preordained, and we were only analyzing the properties of some eternal universe.

Nowhere is it better illustrated than in the Functional Reactive Programming approach to user interaction. Instead of writing separate handlers for every possible user action, all having access to some shared mutable state, FRP treats external events as an infinite list, and applies a series of transformations to it. Conceptually, the list of all our future actions is there, available as the input data to our program. From a program’s perspective there’s no difference between the list of digits of π, a list of pseudo-random numbers, or a list of mouse positions coming through computer hardware. In each case, if you want to get the nth item, you have to first go through the first n-1 items. When applied to temporal events, we call this property causality.

So what does it have to do with category theory? I will argue that category theory encourages a global approach and therefore supports declarative programming. First of all, unlike calculus, it has no built-in notion of distance, or neighborhood, or time. All we have is abstract objects and abstract connections between them. If you can get from A to B through a series of steps, you can also get there in one leap. Moreover, the major tool of category theory is the universal construction, which is the epitome of a global approach. We’ve seen it in action, for instance, in the definition of the categorical product. It was done by specifying its properties — a very declarative approach. It’s an object equipped with two projections, and it’s the best such object — it optimizes a certain property: the property of factorizing the projections of other such objects.

Compare this with Fermat’s principle of minimum time, or the principle of least action.

Conversely, contrast this with the traditional definition of a cartesian product, which is much more imperative. You describe how to create an element of the product by picking one element from one set and another element from another set. It’s a recipe for creating a pair. And there’s another for disassembling a pair.

In almost every programming language, including functional languages like Haskell, product types, coproduct types, and function types are built in, rather than being defined by universal constructions; although there have been attempts at creating categorical programming languages (see, e.g., Tatsuya Hagino’s thesis in Bibliography).

Whether used directly or not, categorical definitions justify pre-existing programming constructs, and give rise to new ones. Most importantly, category theory provides a meta-language for reasoning about computer programs at a declarative level. It also encourages reasoning about problem specification before it is cast into code.

Next Limits and Colimits.

Acknowledgments

I’d like to thank Gershom Bazerman for checking my math and logic, and André van Meulebrouck, who has been volunteering his editing help.
Follow @BartoszMilewski

Bibliography

Tatsuya Hagino, A Categorical Programming Language.

April 15, 2015

Limits and Colimits

Posted by Bartosz Milewski under Category Theory
[60] Comments

This is part 12 of Categories for Programmers. Previously: Declarative Programming. See the Table of Contents.

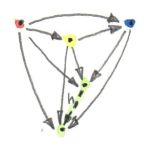
It seems like in category theory everything is related to everything and everything can be viewed from many angles. Take for instance the universal construction of the product. Now that we know more about functors and natural transformations, can we simplify and, possibly, generalize it? Let us try.

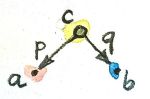
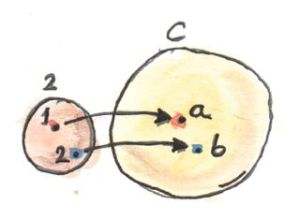
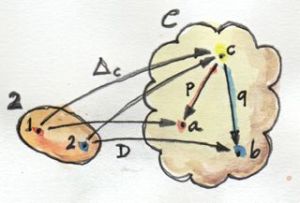
The construction of a product starts with the selection of two objects a and b, whose product we want to construct. But what does it mean to select objects? Can we rephrase this action in more categorical terms? Two objects form a pattern — a very simple pattern. We can abstract this pattern into a category — a very simple category, but a category nevertheless. It’s a category that we’ll call 2. It contains just two objects, 1 and 2, and no morphisms other than the two obligatory identities. Now we can rephrase the selection of two objects in C as the act of defining a functor D from the category 2 to C. A functor maps objects to objects, so its image is just two objects (or it could be one, if the functor collapses objects, which is fine too). It also maps morphisms — in this case it simply maps identity morphisms to identity morphisms.

What’s great about this approach is that it builds on categorical notions, eschewing the imprecise descriptions like “selecting objects,” taken straight from the hunter-gatherer lexicon of our ancestors. And, incidentally, it is also easily generalized, because nothing can stop us from using categories more complex than 2 to define our patterns.

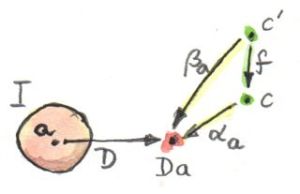
But let’s continue. The next step in the definition of a product is the selection of the candidate object c. Here again, we could rephrase the selection in terms of a functor from a singleton category. And indeed, if we were using Kan extensions, that would be the right thing to do. But since we are not ready for Kan extensions yet, there is another trick we can use: a constant functor Δ from the same category 2 to C. The selection of c in C can be done with Δ_c. Remember, Δ_c maps all objects into c and all morphisms into id_c.

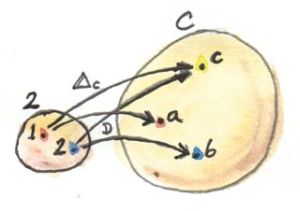
Now we have two functors, Δ_c and D going between 2 and C so it’s only natural to ask about natural transformations between them. Since there are only two objects in 2, a natural transformation will have two components. Object 1 in 2 is mapped to c by Δ_c and to a by D. So the component of a natural transformation between Δ_c and D at 1 is a morphism from c to a. We can call it p. Similarly, the second component is a morphism q from c to b — the image of the object 2 in 2 under D. But these are exactly like the two projections we used in our original definition of the product. So instead of talking about selecting objects and projections, we can just talk about picking functors and natural transformations. It so happens that in this simple case the naturality condition for our transformation is trivially satisfied, because there are no morphisms (other than the identities) in 2.

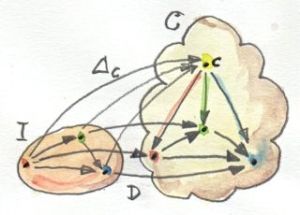
A generalization of this construction to categories other than 2 — ones that, for instance, contain non-trivial morphisms — will impose naturality conditions on the transformation between Δ_c and D. We call such transformation a cone, because the image of Δ is the apex of a cone/pyramid whose sides are formed by the components of the natural transformation. The image of D forms the base of the cone.

In general, to build a cone, we start with a category I that defines the pattern. It’s a small, often finite category. We pick a functor D from I to C and call it (or its image) a diagram. We pick some c in C as the apex of our cone. We use it to define the constant functor Δ_c from I to C. A natural transformation from Δ_c to D is then our cone. For a finite I it’s just a bunch of morphisms connecting c to the diagram: the image of I under D.

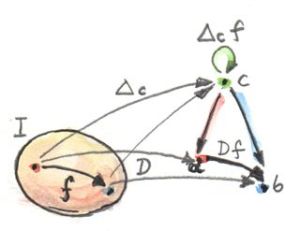
Naturality requires that all triangles (the walls of the pyramid) in this diagram commute. Indeed, take any morphism f in I. The functor D maps it to a morphism D f in C, a morphism that forms the base of some triangle. The constant functor Δ_c maps f to the identity morphism on c. Δ squishes the two ends of the morphism into one object, and the naturality square becomes a commuting triangle. The two arms of this triangle are the components of the natural transformation.

So that’s one cone. What we are interested in is the universal cone — just like we picked a universal object for our definition of a product.

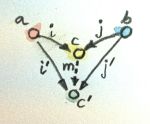
There are many ways to go about it. For instance, we may define a category of cones based on a given functor D. Objects in that category are cones. Not every object c in C can be an apex of a cone, though, because there may be no natural transformation between Δ_c and D.

To make it a category, we also have to define morphisms between cones. These would be fully determined by morphisms between their apexes. But not just any morphism will do. Remember that, in our construction of the product, we imposed the condition that the morphisms between candidate objects (the apexes) must be common factors for the projections. For instance:

p' = p . m
q' = q . m

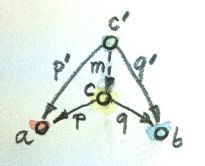
This condition translates, in the general case, to the condition that the triangles whose one side is the factorizing morphism all commute.

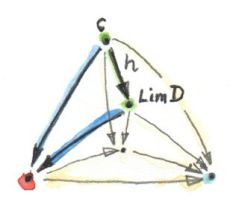
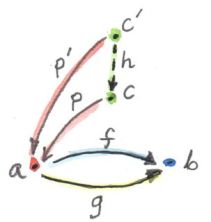
The commuting triangle connecting two cones, with the factorizing morphism h (here, the lower cone is the universal one, with Lim D as its apex).

We’ll take those factorizing morphisms as the morphisms in our category of cones. It’s easy to check that those morphisms indeed compose, and that the identity morphism is a factorizing morphism as well. Cones therefore form a category.

Now we can define the universal cone as the terminal object in the category of cones. The definition of the terminal object states that there is a unique morphism from any other object to that object. In our case it means that there is a unique factorizing morphism from the apex of any other cone to the apex of the universal cone. We call this universal cone the limit of the diagram D, Lim D (in the literature, you’ll often see a left arrow pointing towards I under the Lim sign). Often, as a shorthand, we call the apex of this cone the limit (or the limit object).

The intuition is that the limit embodies the properties of the whole diagram in a single object. For instance, the limit of our two-object diagram is the product of two objects. The product (together with the two projections) contains the information about both objects. And being universal means that it has no extraneous junk.

Limit as a Natural Isomorphism

There is still something unsatisfying about this definition of a limit. I mean, it’s workable, but we still have this commutativity condition for the triangles that are linking any two cones. It would be so much more elegant if we could replace it with some naturality condition. But how?

We are no longer dealing with one cone but with a whole collection (in fact, a category) of cones. If the limit exists (and — let’s make it clear — there’s no guarantee of that), one of those cones is the universal cone. For every other cone we have a unique factorizing morphism that maps its apex, let’s call it c, to the apex of the universal cone, which we named Lim D. (In fact, I can skip the word “other,” because the identity morphism maps the universal cone to itself and it trivially factorizes through itself.) Let me repeat the important part: given any cone, there is a unique morphism of a special kind. We have a mapping of cones to special morphisms, and it’s a one-to-one mapping.

This special morphism is a member of the hom-set C(c, Lim D). The other members of this hom-set are less fortunate, in the sense that they don’t factorize the mapping of the two cones. What we want is to be able to pick, for each c, one morphism from the set C(c, Lim D) — a morphism that satisfies the particular commutativity condition. Does that sound like defining a natural transformation? It most certainly does!

But what are the functors that are related by this transformation?

One functor is the mapping of c to the set C(c, Lim D). It’s a functor from C to Set — it maps objects to sets. In fact it’s a contravariant functor. Here’s how we define its action on morphisms: Let’s take a morphism f from c' to c:

f :: c' -> c

Our functor maps c' to the set C(c', Lim D). To define the action of this functor on f (in other words, to lift f), we have to define the corresponding mapping between C(c, Lim D) and C(c', Lim D). So let’s pick one element u of C(c, Lim D) and see if we can map it to some element of C(c', Lim D). An element of a hom-set is a morphism, so we have:

u :: c -> Lim D

We can precompose u with f to get:

u . f :: c' -> Lim D

And that’s an element of C(c', Lim D)— so indeed, we have found a mapping of morphisms:

contramap :: (c' -> c) -> (c -> Lim D) -> (c' -> Lim D)
contramap f u = u . f

Notice the inversion in the order of c and c' characteristic of a contravariant functor.

To define a natural transformation, we need another functor that’s also a mapping from C to Set. But this time we’ll consider a set of cones. Cones are just natural transformations, so we are looking at the set of natural transformations Nat(Δ_c, D). The mapping from c to this particular set of natural transformations is a (contravariant) functor. How can we show that? Again, let’s define its action on a morphism:

f :: c' -> c

The lifting of f should be a mapping of natural transformations between two functors that go from I to C:

Nat(Δ_c, D) -> Nat(Δ_c', D)

How do we map natural transformations? Every natural transformation is a selection of morphisms — its components — one morphism per element of I. A component of some α (a member of Nat(Δ_c, D)) at a (an object in I) is a morphism:

α_a :: Δ_ca -> D a

or, using the definition of the constant functor Δ,

α_a :: c -> D a

Given f and α, we have to construct a β, a member of Nat(Δ_c', D). Its component at a should be a morphism:

β_a :: c' -> D a

We can easily get the latter from the former by precomposing it with f:

β_a = α_a . f

It’s relatively easy to show that those components indeed add up to a natural transformation.

Given our morphism f, we have thus built a mapping between two natural transformations, component-wise. This mapping defines contramap for the functor:

c -> Nat(Δ_c, D)

What I have just done is to show you that we have two (contravariant) functors from C to Set. I haven’t made any assumptions — these functors always exist.

Incidentally, the first of these functors plays an important role in category theory, and we’ll see it again when we talk about Yoneda’s lemma. There is a name for contravariant functors from any category C to Set: they are called “presheaves.” This one is called a representable presheaf. The second functor is also a presheaf.

Now that we have two functors, we can talk about natural transformations between them. So without further ado, here’s the conclusion: A functor D from I to C has a limit Lim D if and only if there is a natural isomorphism between the two functors I have just defined:

C(c, Lim D) ≃ Nat(Δ_c, D)

Let me remind you what a natural isomorphism is. It’s a natural transformation whose every component is an isomorphism, that is to say an invertible morphism.

I’m not going to go through the proof of this statement. The procedure is pretty straightforward if not tedious. When dealing with natural transformations, you usually focus on components, which are morphisms. In this case, since the target of both functors is Set, the components of the natural isomorphism will be functions. These are higher order functions, because they go from the hom-set to the set of natural transformations. Again, you can analyze a function by considering what it does to its argument: here the argument will be a morphism — a member of C(c, Lim D) — and the result will be a natural transformation — a member of Nat(Δ_c, D), or what we have called a cone. This natural transformation, in turn, has its own components, which are morphisms. So it’s morphisms all the way down, and if you can keep track of them, you can prove the statement.

The most important result is that the naturality condition for this isomorphism is exactly the commutativity condition for the mapping of cones.

As a preview of coming attractions, let me mention that the set Nat(Δ_c, D) can be thought of as a hom-set in the functor category; so our natural isomorphism relates two hom-sets, which points at an even more general relationship called an adjunction.

Examples of Limits

We’ve seen that the categorical product is a limit of a diagram generated by a simple category we called 2.

There is an even simpler example of a limit: the terminal object. The first impulse would be to think of a singleton category as leading to a terminal object, but the truth is even starker than that: the terminal object is a limit generated by an empty category. A functor from an empty category selects no object, so a cone shrinks to just the apex. The universal cone is the lone apex that has a unique morphism coming to it from any other apex. You will recognize this as the definition of the terminal object.

The next interesting limit is called the equalizer. It’s a limit generated by a two-element category with two parallel morphisms going between them (and, as always, the identity morphisms). This category selects a diagram in C consisting of two objects, a and b, and two morphisms:

f :: a -> b
g :: a -> b

To build a cone over this diagram, we have to add the apex, c and two projections:

p :: c -> a
q :: c -> b

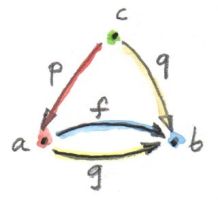
We have two triangles that must commute:

q = f . p
q = g . p

This tells us that q is uniquely determined by one of these equations, say, q = f . p, and we can omit it from the picture. So we are left with just one condition:

f . p = g . p

The way to think about it is that, if we restrict our attention to Set, the image of the function p selects a subset of a. When restricted to this subset, the functions f and g are equal.

For instance, take a to be the two-dimensional plane parameterized by coordinates x and y. Take b to be the real line, and take:

f (x, y) = 2 * y + x
g (x, y) = y - x

The equalizer for these two functions is the set of real numbers (the apex, c) and the function:

p t = (t, (-2) * t)

Notice that (p t) defines a straight line in the two-dimensional plane. Along this line, the two functions are equal.

Of course, there are other sets c' and functions p' that may lead to the equality:

f . p' = g . p'

but they all uniquely factor out through p. For instance, we can take the singleton set () as c' and the function:

p'() = (0, 0)

It’s a good cone, because f (0, 0) = g (0, 0). But it’s not universal, because of the unique factorization through h:

p' = p . h

with

h () = 0

An equalizer can thus be used to solve equations of the type f x = g x. But it’s much more general, because it’s defined in terms of objects and morphisms rather than algebraically.

An even more general idea of solving an equation is embodied in another limit — the pullback. Here, we still have two morphisms that we want to equate, but this time their domains are different. We start with a three-object category of the shape: 1->2<-3. The diagram corresponding to this category consists of three objects, a, b, and c, and two morphisms:

f :: a -> b
g :: c -> b

This diagram is often called a cospan.

A cone built on top of this diagram consists of the apex, d, and three morphisms:

p :: d -> a
q :: d -> c
r :: d -> b

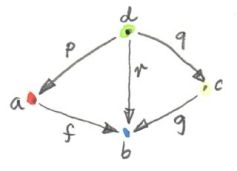
Commutativity conditions tell us that r is completely determined by the other morphisms, and can be omitted from the picture. So we are only left with the following condition:

g . q = f . p

A pullback is a universal cone of this shape.

Again, if you narrow your focus down to sets, you can think of the object d as consisting of pairs of elements from a and c for which f acting on the first component is equal to g acting on the second component. If this is still too general, consider the special case in which g is a constant function, say g _ = 1.23 (assuming that b is a set of real numbers). Then you are really solving the equation:

f x = 1.23

In this case, the choice of c is irrelevant (as long as it’s not an empty set), so we can take it to be a singleton set. The set a could, for instance, be the set of three-dimensional vectors, and f the vector length. Then the pullback is the set of pairs (v, ()), where v is a vector of length 1.23 (a solution to the equation sqrt (x²+y²+z²) = 1.23), and () is the dummy element of the singleton set.

But pullbacks have more general applications, also in programming. For instance, consider C++ classes as a category in which morphism are arrows that connect subclasses to superclasses. We’ll consider inheritance a transitive property, so if C inherits from B and B inherits from A then we’ll say that C inherits from A (after all, you can pass a pointer to C where a pointer to A is expected). Also, we’ll assume that C inherits from C, so we have the identity arrow for every class. This way subclassing is aligned with subtyping. C++ also supports multiple inheritance, so you can construct a diamond inheritance diagram with two classes B and C inheriting from A, and a fourth class D multiply inheriting from B and C. Normally, D would get two copies of A, which is rarely desirable; but you can use virtual inheritance to have just one copy of A in D.

What would it mean to have D be a pullback in this diagram? It would mean that any class E that multiply inherits from B and C is also a subclass of D. This is not directly expressible in C++, where subtyping is nominal (the C++ compiler wouldn’t infer this kind of class relationship — it would require “duck typing”). But we could go outside of the subtyping relationship and instead ask whether a cast from E to D would be safe or not. This cast would be safe if D were the bare-bone combination of B and C, with no additional data and no overriding of methods. And, of course, there would be no pullback if there is a name conflict between some methods of B and C.

There’s also a more advanced use of a pullback in type inference. There is often a need to unify types of two expressions. For instance, suppose that the compiler wants to infer the type of a function:

twice f x = f (f x)

It will assign preliminary types to all variables and sub-expressions. In particular, it will assign:

f       :: t0
x       :: t1
f x     :: t2
f (f x) :: t3

from which it will deduce that:

twice :: t0 -> t1 -> t3

It will also come up with a set of constraints resulting from the rules of function application:

t0 = t1 -> t2 -- because f is applied to x
t0 = t2 -> t3 -- because f is applied to (f x)

These constraints have to be unified by finding a set of types (or type variables) that, when substituted for the unknown types in both expressions, produce the same type. One such substitution is:

t1 = t2 = t3 = Int
twice :: (Int -> Int) -> Int -> Int

but, obviously, it’s not the most general one. The most general substitution is obtained using a pullback. I won’t go into the details, because they are beyond the scope of this book, but you can convince yourself that the result should be:

twice :: (t -> t) -> t -> t

with t a free type variable.

Colimits

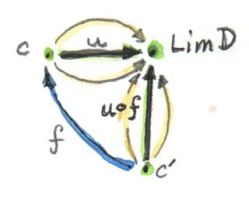
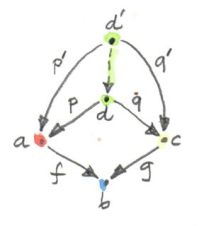
Just like all constructions in category theory, limits have their dual image in opposite categories. When you invert the direction of all arrows in a cone, you get a co-cone, and the universal one of those is called a colimit. Notice that the inversion also affects the factorizing morphism, which now flows from the universal co-cone to any other co-cone.

Cocone with a factorizing morphism h connecting two apexes.

A typical example of a colimit is a coproduct, which corresponds to the diagram generated by 2, the category we’ve used in the definition of the product.

Both the product and the coproduct embody the essence of a pair of objects, each in a different way.

Just like the terminal object was a limit, so the initial object is a colimit corresponding to the diagram based on an empty category.

The dual of the pullback is called the pushout. It’s based on a diagram called a span, generated by the category 1<-2->3.

Continuity

I said previously that functors come close to the idea of continuous mappings of categories, in the sense that they never break existing connections (morphisms). The actual definition of a continuous functor F from a category C to C’ includes the requirement that the functor preserve limits. Every diagram D in C can be mapped to a diagram F ∘ D in C’ by simply composing two functors. The continuity condition for F states that, if the diagram D has a limit Lim D, then the diagram F ∘ D also has a limit, and it is equal to F (Lim D).

Notice that, because functors map morphisms to morphisms, and compositions to compositions, an image of a cone is always a cone. A commuting triangle is always mapped to a commuting triangle (functors preserve composition). The same is true for the factorizing morphisms: the image of a factorizing morphism is also a factorizing morphism. So every functor is almost continuous. What may go wrong is the uniqueness condition. The factorizing morphism in C’ might not be unique. There may also be other “better cones” in C’ that were not available in C.

A hom-functor is an example of a continuous functor. Recall that the hom-functor, C(a, b), is contravariant in the first variable and covariant in the second. In other words, it’s a functor:

C^op × C -> Set

When its second argument is fixed, the hom-set functor (which becomes the representable presheaf) maps colimits in C to limits in Set; and when its first argument is fixed, it maps limits to limits.

In Haskell, a hom-functor is the mapping of any two types to a function type, so it’s just a parameterized function type. When we fix the second parameter, let’s say to String, we get the contravariant functor:

newtype ToString a = ToString (a -> String)
instance Contravariant ToString where
    contramap f (ToString g) = ToString (g . f)

Continuity means that when ToString is applied to a colimit, for instance a coproduct Either b c, it will produce a limit; in this case a product of two function types:

ToString (Either b c) ~ (b -> String, c -> String)

Indeed, any function of Either b c is implemented as a case statement with the two cases being serviced by a pair of functions.

Similarly, when we fix the first argument of the hom-set, we get the familiar reader functor. Its continuity means that, for instance, any function returning a product is equivalent to a product of functions; in particular:

r -> (a, b) ~ (r -> a, r -> b)

I know what you’re thinking: You don’t need category theory to figure these things out. And you’re right! Still, I find it amazing that such results can be derived from first principles with no recourse to bits and bytes, processor architectures, compiler technologies, or even lambda calculus.

If you’re curious where the names “limit” and “continuity” come from, they are a generalization of the corresponding notions from calculus. In calculus limits and continuity are defined in terms of open neighborhoods. Open sets, which define topology, form a category (a poset).

Challenges

How would you describe a pushout in the category of C++ classes?
Show that the limit of the identity functor Id :: C -> C is the initial object.
Subsets of a given set form a category. A morphism in that category is defined to be an arrow connecting two sets if the first is the subset of the second. What is a pullback of two sets in such a category? What’s a pushout? What are the initial and terminal objects?
Can you guess what a coequalizer is?
Show that, in a category with a terminal object, a pullback towards the terminal object is a product.
Similarly, show that a pushout from an initial object (if one exists) is the coproduct.

Next: Free Monoids.

Acknowledgments

I’d like to thank Gershom Bazerman for checking my math and logic, and André van Meulebrouck, who has been volunteering his editing help.
Follow @BartoszMilewski

April 7, 2015

Natural Transformations

Posted by Bartosz Milewski under Category Theory, Functional Programming, Haskell, Programming
[63] Comments

This is part 10 of Categories for Programmers. Previously: Function Types. See the Table of Contents.

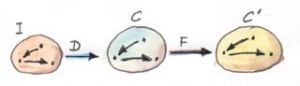
We talked about functors as mappings between categories that preserve their structure. A functor “embeds” one category in another. It may collapse multiple things into one, but it never breaks connections. One way of thinking about it is that with a functor we are modeling one category inside another. The source category serves as a model, a blueprint, for some structure that’s part of the target category.

There may be many ways of embedding one category in another. Sometimes they are equivalent, sometimes very different. One may collapse the whole source category into one object, another may map every object to a different object and every morphism to a different morphism. The same blueprint may be realized in many different ways. Natural transformations help us compare these realizations. They are mappings of functors — special mappings that preserve their functorial nature.

Consider two functors F and G between categories C and D. If you focus on just one object a in C, it is mapped to two objects: F a and G a. A mapping of functors should therefore map F a to G a.

Notice that F a and G a are objects in the same category D. Mappings between objects in the same category should not go against the grain of the category. We don’t want to make artificial connections between objects. So it’s natural to use existing connections, namely morphisms. A natural transformation is a selection of morphisms: for every object a, it picks one morphism from F a to G a. If we call the natural transformation α, this morphism is called the component of α at a, or α_a.

α_a :: F a -> G a

Keep in mind that a is an object in C while α_a is a morphism in D.

If, for some a, there is no morphism between F a and G a in D, there can be no natural transformation between F and G.

Of course that’s only half of the story, because functors not only map objects, they map morphisms as well. So what does a natural transformation do with those mappings? It turns out that the mapping of morphisms is fixed — under any natural transformation between F and G, F f must be transformed into G f. What’s more, the mapping of morphisms by the two functors drastically restricts the choices we have in defining a natural transformation that’s compatible with it. Consider a morphism f between two objects a and b in C. It’s mapped to two morphisms, F f and G f in D:

F f :: F a -> F b
G f :: G a -> G b

The natural transformation α provides two additional morphisms that complete the diagram in D:

α_a :: F a -> G a
α_b :: F b -> G b

Now we have two ways of getting from F a to G b. To make sure that they are equal, we must impose the naturality condition that holds for any f:

G f ∘ α_a = α_b ∘ F f

The naturality condition is a pretty stringent requirement. For instance, if the morphism F f is invertible, naturality determines α_b in terms of α_a. It transports α_a along f:

α_b = (G f) ∘ α_a ∘ (F f)^-1

If there is more than one invertible morphism between two objects, all these transports have to agree. In general, though, morphisms are not invertible; but you can see that the existence of natural transformations between two functors is far from guaranteed. So the scarcity or the abundance of functors that are related by natural transformations may tell you a lot about the structure of categories between which they operate. We’ll see some examples of that when we talk about limits and the Yoneda lemma.

Looking at a natural transformation component-wise, one may say that it maps objects to morphisms. Because of the naturality condition, one may also say that it maps morphisms to commuting squares — there is one commuting naturality square in D for every morphism in C.

This property of natural transformations comes in very handy in a lot of categorical constructions, which often include commuting diagrams. With a judicious choice of functors, a lot of these commutativity conditions may be transformed into naturality conditions. We’ll see examples of that when we get to limits, colimits, and adjunctions.

Finally, natural transformations may be used to define isomorphisms of functors. Saying that two functors are naturally isomorphic is almost like saying they are the same. Natural isomorphism is defined as a natural transformation whose components are all isomorphisms (invertible morphisms).

Polymorphic Functions

We talked about the role of functors (or, more specifically, endofunctors) in programming. They correspond to type constructors that map types to types. They also map functions to functions, and this mapping is implemented by a higher order function fmap (or transform, then, and the like in C++).

To construct a natural transformation we start with an object, here a type, a. One functor, F, maps it to the type F a. Another functor, G, maps it to G a. The component of a natural transformation alpha at a is a function from F a to G a. In pseudo-Haskell:

alpha_a :: F a -> G a

A natural transformation is a polymorphic function that is defined for all types a:

alpha :: forall a . F a -> G a

The forall a is optional in Haskell (and in fact requires turning on the language extension ExplicitForAll). Normally, you would write it like this:

alpha :: F a -> G a

Keep in mind that it’s really a family of functions parameterized by a. This is another example of the terseness of the Haskell syntax. A similar construct in C++ would be slightly more verbose:

template<class A> G<A> alpha(F<A>);

There is a more profound difference between Haskell’s polymorphic functions and C++ generic functions, and it’s reflected in the way these functions are implemented and type-checked. In Haskell, a polymorphic function must be defined uniformly for all types. One formula must work across all types. This is called parametric polymorphism.

C++, on the other hand, supports by default ad hoc polymorphism, which means that a template doesn’t have to be well-defined for all types. Whether a template will work for a given type is decided at instantiation time, where a concrete type is substituted for the type parameter. Type checking is deferred, which unfortunately often leads to incomprehensible error messages.

In C++, there is also a mechanism for function overloading and template specialization, which allows different definitions of the same function for different types. In Haskell this functionality is provided by type classes and type families.

Haskell’s parametric polymorphism has an unexpected consequence: any polymorphic function of the type:

alpha :: F a -> G a

where F and G are functors, automatically satisfies the naturality condition. Here it is in categorical notation (f is a function f::a->b):

G f ∘ α_a = α_b ∘ F f

In Haskell, the action of a functor G on a morphism f is implemented using fmap. I’ll first write it in pseudo-Haskell, with explicit type annotations:

fmap_G f . alpha_a = alpha_b . fmap_F f

Because of type inference, these annotations are not necessary, and the following equation holds:

fmap f . alpha = alpha . fmap f

This is still not real Haskell — function equality is not expressible in code — but it’s an identity that can be used by the programmer in equational reasoning; or by the compiler, to implement optimizations.

The reason why the naturality condition is automatic in Haskell has to do with “theorems for free.” Parametric polymorphism, which is used to define natural transformations in Haskell, imposes very strong limitations on the implementation — one formula for all types. These limitations translate into equational theorems about such functions. In the case of functions that transform functors, free theorems are the naturality conditions. [You may read more about free theorems in my blog Parametricity: Money for Nothing and Theorems for Free.]

One way of thinking about functors in Haskell that I mentioned earlier is to consider them generalized containers. We can continue this analogy and consider natural transformations to be recipes for repackaging the contents of one container into another container. We are not touching the items themselves: we don’t modify them, and we don’t create new ones. We are just copying (some of) them, sometimes multiple times, into a new container.

The naturality condition becomes the statement that it doesn’t matter whether we modify the items first, through the application of fmap, and repackage later; or repackage first, and then modify the items in the new container, with its own implementation of fmap. These two actions, repackaging and fmapping, are orthogonal. “One moves the eggs, the other boils them.”

Let’s see a few examples of natural transformations in Haskell. The first is between the list functor, and the Maybe functor. It returns the head of the list, but only if the list is non-empty:

safeHead :: [a] -> Maybe a
safeHead [] = Nothing
safeHead (x:xs) = Just x

It’s a function polymorphic in a. It works for any type a, with no limitations, so it is an example of parametric polymorphism. Therefore it is a natural transformation between the two functors. But just to convince ourselves, let’s verify the naturality condition.

fmap f . safeHead = safeHead . fmap f

We have two cases to consider; an empty list:

fmap f (safeHead []) = fmap f Nothing = Nothing

safeHead (fmap f []) = safeHead [] = Nothing

and a non-empty list:

fmap f (safeHead (x:xs)) = fmap f (Just x) = Just (f x)

safeHead (fmap f (x:xs)) = safeHead (f x : fmap f xs) = Just (f x)

I used the implementation of fmap for lists:

fmap f [] = []
fmap f (x:xs) = f x : fmap f xs

and for Maybe:

fmap f Nothing = Nothing
fmap f (Just x) = Just (f x)

An interesting case is when one of the functors is the trivial Const functor. A natural transformation from or to a Const functor looks just like a function that’s either polymorphic in its return type or in its argument type.

For instance, length can be thought of as a natural transformation from the list functor to the Const Int functor:

length :: [a] -> Const Int a
length [] = Const 0
length (x:xs) = Const (1 + unConst (length xs))

Here, unConst is used to peel off the Const constructor:

unConst :: Const c a -> c
unConst (Const x) = x

Of course, in practice length is defined as:

length :: [a] -> Int

which effectively hides the fact that it’s a natural transformation.

Finding a parametrically polymorphic function from a Const functor is a little harder, since it would require the creation of a value from nothing. The best we can do is:

scam :: Const Int a -> Maybe a
scam (Const x) = Nothing

Another common functor that we’ve seen already, and which will play an important role in the Yoneda lemma, is the Reader functor. I will rewrite its definition as a newtype:

newtype Reader e a = Reader (e -> a)

It is parameterized by two types, but is (covariantly) functorial only in the second one:

instance Functor (Reader e) where  
    fmap f (Reader g) = Reader (\x -> f (g x))

For every type e, you can define a family of natural transformations from Reader e to any other functor f. We’ll see later that the members of this family are always in one to one correspondence with the elements of f e (the Yoneda lemma).

For instance, consider the somewhat trivial unit type () with one element (). The functor Reader () takes any type a and maps it into a function type ()->a. These are just all the functions that pick a single element from the set a. There are as many of these as there are elements in a. Now let’s consider natural transformations from this functor to the Maybe functor:

alpha :: Reader () a -> Maybe a

There are only two of these, dumb and obvious:

dumb (Reader _) = Nothing

and

obvious (Reader g) = Just (g ())

(The only thing you can do with g is to apply it to the unit value ().)

And, indeed, as predicted by the Yoneda lemma, these correspond to the two elements of the Maybe () type, which are Nothing and Just (). We’ll come back to the Yoneda lemma later — this was just a little teaser.

Beyond Naturality

A parametrically polymorphic function between two functors (including the edge case of the Const functor) is always a natural transformation. Since all standard algebraic data types are functors, any polymorphic function between such types is a natural transformation.

We also have function types at our disposal, and those are functorial in their return type. We can use them to build functors (like the Reader functor) and define natural transformations that are higher-order functions.

However, function types are not covariant in the argument type. They are contravariant. Of course contravariant functors are equivalent to covariant functors from the opposite category. Polymorphic functions between two contravariant functors are still natural transformations in the categorical sense, except that they work on functors from the opposite category to Haskell types.

You might remember the example of a contravariant functor we’ve looked at before:

newtype Op r a = Op (a -> r)

This functor is contravariant in a:

instance Contravariant (Op r) where
    contramap f (Op g) = Op (g . f)

We can write a polymorphic function from, say, Op Bool to Op String:

predToStr (Op f) = Op (\x -> if f x then "T" else "F")

But since the two functors are not covariant, this is not a natural transformation in Hask. However, because they are both contravariant, they satisfy the “opposite” naturality condition:

contramap f . predToStr = predToStr . contramap f

Notice that the function f must go in the opposite direction than what you’d use with fmap, because of the signature of contramap:

contramap :: (b -> a) -> (Op Bool a -> Op Bool b)

Are there any type constructors that are not functors, whether covariant or contravariant? Here’s one example:

a -> a

This is not a functor because the same type a is used both in the negative (contravariant) and positive (covariant) position. You can’t implement fmap or contramap for this type. Therefore a function of the signature:

(a -> a) -> f a

where f is an arbitrary functor, cannot be a natural transformation. Interestingly, there is a generalization of natural transformations, called dinatural transformations, that deals with such cases. We’ll get to them when we discuss ends.

Functor Category

Now that we have mappings between functors — natural transformations — it’s only natural to ask the question whether functors form a category. And indeed they do! There is one category of functors for each pair of categories, C and D. Objects in this category are functors from C to D, and morphisms are natural transformations between those functors.

We have to define composition of two natural transformations, but that’s quite easy. The components of natural transformations are morphisms, and we know how to compose morphisms.

Indeed, let’s take a natural transformation α from functor F to G. Its component at object a is some morphism:

α_a :: F a -> G a

We’d like to compose α with β, which is a natural transformation from functor G to H. The component of β at a is a morphism:

β_a :: G a -> H a

These morphisms are composable and their composition is another morphism:

β_a ∘ α_a :: F a -> H a

We will use this morphism as the component of the natural transformation β ⋅ α — the composition of two natural transformations β after α:

(β ⋅ α)_a = β_a ∘ α_a

One (long) look at a diagram convinces us that the result of this composition is indeed a natural transformation from F to H:

H f ∘ (β ⋅ α)_a = (β ⋅ α)_b ∘ F f

Composition of natural transformations is associative, because their components, which are regular morphisms, are associative with respect to their composition.

Finally, for each functor F there is an identity natural transformation 1_F whose components are the identity morphisms:

id_{F a} :: F a -> F a

So, indeed, functors form a category.

A word about notation. Following Saunders Mac Lane I use the dot for the kind of natural transformation composition I have just described. The problem is that there are two ways of composing natural transformations. This one is called the vertical composition, because the functors are usually stacked up vertically in the diagrams that describe it. Vertical composition is important in defining the functor category. I’ll explain horizontal composition shortly.

The functor category between categories C and D is written as Fun(C, D), or [C, D], or sometimes as D^C. This last notation suggests that a functor category itself might be considered a function object (an exponential) in some other category. Is this indeed the case?

Let’s have a look at the hierarchy of abstractions that we’ve been building so far. We started with a category, which is a collection of objects and morphisms. Categories themselves (or, strictly speaking small categories, whose objects form sets) are themselves objects in a higher-level category Cat. Morphisms in that category are functors. A Hom-set in Cat is a set of functors. For instance Cat(C, D) is a set of functors between two categories C and D.

A functor category [C, D] is also a set of functors between two categories (plus natural transformations as morphisms). Its objects are the same as the members of Cat(C, D). Moreover, a functor category, being a category, must itself be an object of Cat (it so happens that the functor category between two small categories is itself small). We have a relationship between a Hom-set in a category and an object in the same category. The situation is exactly like the exponential object that we’ve seen in the last section. Let’s see how we can construct the latter in Cat.

As you may remember, in order to construct an exponential, we need to first define a product. In Cat, this turns out to be relatively easy, because small categories are sets of objects, and we know how to define cartesian products of sets. So an object in a product category C × D is just a pair of objects, (c, d), one from C and one from D. Similarly, a morphism between two such pairs, (c, d) and (c', d'), is a pair of morphisms, (f, g), where f :: c -> c' and g :: d -> d'. These pairs of morphisms compose component-wise, and there is always an identity pair that is just a pair of identity morphisms. To make the long story short, Cat is a full-blown cartesian closed category in which there is an exponential object D^C for any pair of categories. And by “object” in Cat I mean a category, so D^C is a category, which we can identify with the functor category between C and D.

2-Categories

With that out of the way, let’s have a closer look at Cat. By definition, any Hom-set in Cat is a set of functors. But, as we have seen, functors between two objects have a richer structure than just a set. They form a category, with natural transformations acting as morphisms. Since functors are considered morphisms in Cat, natural transformations are morphisms between morphisms.

This richer structure is an example of a 2-category, a generalization of a category where, besides objects and morphisms (which might be called 1-morphisms in this context), there are also 2-morphisms, which are morphisms between morphisms.

In the case of Cat seen as a 2-category we have:

Objects: (Small) categories
1-morphisms: Functors between categories
2-morphisms: Natural transformations between functors.

Instead of a Hom-set between two categories C and D, we have a Hom-category — the functor category D^C. We have regular functor composition: a functor F from D^C composes with a functor G from E^D to give G ∘ F from E^C. But we also have composition inside each Hom-category — vertical composition of natural transformations, or 2-morphisms, between functors.

With two kinds of composition in a 2-category, the question arises: How do they interact with each other?

Let’s pick two functors, or 1-morphisms, in Cat:

F :: C -> D
G :: D -> E

and their composition:

G ∘ F :: C -> E

Suppose we have two natural transformations, α and β, that act, respectively, on functors F and G:

α :: F -> F'
β :: G -> G'

Notice that we cannot apply vertical composition to this pair, because the target of α is different from the source of β. In fact they are members of two different functor categories: D ^C and E ^D. We can, however, apply composition to the functors F’ and G’, because the target of F’ is the source of G’ — it’s the category D. What’s the relation between the functors G’∘ F’ and G ∘ F?

Having α and β at our disposal, can we define a natural transformation from G ∘ F to G’∘ F’? Let me sketch the construction.

As usual, we start with an object a in C. Its image splits into two objects in D: F a and F'a. There is also a morphism, a component of α, connecting these two objects:

α_a :: F a -> F'a

When going from D to E, these two objects split further into four objects:

G (F a), G'(F a), G (F'a), G'(F'a)

We also have four morphisms forming a square. Two of these morphisms are the components of the natural transformation β:

β_{F a} :: G (F a) -> G'(F a)
β_F'a :: G (F'a) -> G'(F'a)

The other two are the images of α_a under the two functors (functors map morphisms):

G α_a :: G (F a) -> G (F'a)
G'α_a :: G'(F a) -> G'(F'a)

That’s a lot of morphisms. Our goal is to find a morphism that goes from G (F a) to G'(F'a), a candidate for the component of a natural transformation connecting the two functors G ∘ F and G’∘ F’. In fact there’s not one but two paths we can take from G (F a) to G'(F'a):

G'α_a ∘ β_{F a}
β_F'a ∘ G α_a

Luckily for us, they are equal, because the square we have formed turns out to be the naturality square for β.

We have just defined a component of a natural transformation from G ∘ F to G’∘ F’. The proof of naturality for this transformation is pretty straightforward, provided you have enough patience.

We call this natural transformation the horizontal composition of α and β:

β ∘ α :: G ∘ F -> G'∘ F'

Again, following Mac Lane I use the small circle for horizontal composition, although you may also encounter star in its place.

Here’s a categorical rule of thumb: Every time you have composition, you should look for a category. We have vertical composition of natural transformations, and it’s part of the functor category. But what about the horizontal composition? What category does that live in?

The way to figure this out is to look at Cat sideways. Look at natural transformations not as arrows between functors but as arrows between categories. A natural transformation sits between two categories, the ones that are connected by the functors it transforms. We can think of it as connecting these two categories.

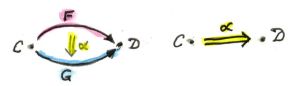
Let’s focus on two objects of Cat — categories C and D. There is a set of natural transformations that go between functors that connect C to D. These natural transformations are our new arrows from C to D. By the same token, there are natural transformations going between functors that connect D to E, which we can treat as new arrows going from D to E. Horizontal composition is the composition of these arrows.

We also have an identity arrow going from C to C. It’s the identity natural transformation that maps the identity functor on C to itself. Notice that the identity for horizontal composition is also the identity for vertical composition, but not vice versa.

Finally, the two compositions satisfy the interchange law:

(β' ⋅ α') ∘ (β ⋅ α) = (β' ∘ β) ⋅ (α' ∘ α)

I will quote Saunders Mac Lane here: The reader may enjoy writing down the evident diagrams needed to prove this fact.

There is one more piece of notation that might come in handy in the future. In this new sideways interpretation of Cat there are two ways of getting from object to object: using a functor or using a natural transformation. We can, however, re-interpret the functor arrow as a special kind of natural transformation: the identity natural transformation acting on this functor. So you’ll often see this notation:

F ∘ α

where F is a functor from D to E, and α is a natural transformation between two functors going from C to D. Since you can’t compose a functor with a natural transformation, this is interpreted as a horizontal composition of the identity natural transformation 1_F after α.

Similarly:

α ∘ F

is a horizontal composition of α after 1_F.

Conclusion

This concludes the first part of the book. We’ve learned the basic vocabulary of category theory. You may think of objects and categories as nouns; and morphisms, functors, and natural transformations as verbs. Morphisms connect objects, functors connect categories, natural transformations connect functors.

But we’ve also seen that, what appears as an action at one level of abstraction, becomes an object at the next level. A set of morphisms turns into a function object. As an object, it can be a source or a target of another morphism. That’s the idea behind higher order functions.

A functor maps objects to objects, so we can use it as a type constructor, or a parametric type. A functor also maps morphisms, so it is a higher order function — fmap. There are some simple functors, like Const, product, and coproduct, that can be used to generate a large variety of algebraic data types. Function types are also functorial, both covariant and contravariant, and can be used to extend algebraic data types.

Functors may be looked upon as objects in the functor category. As such, they become sources and targets of morphisms: natural transformations. A natural transformation is a special type of polymorphic function.

Challenges

Define a natural transformation from the Maybe functor to the list functor. Prove the naturality condition for it.
Define at least two different natural transformations between Reader () and the list functor. How many different lists of () are there?
Continue the previous exercise with Reader Bool and Maybe.
Show that horizontal composition of natural transformation satisfies the naturality condition (hint: use components). It’s a good exercise in diagram chasing.
Write a short essay about how you may enjoy writing down the evident diagrams needed to prove the interchange law.
Create a few test cases for the opposite naturality condition of transformations between different Op functors. Here’s one choice:
```
op :: Op Bool Int
op = Op (\x -> x > 0)
```
and
```
f :: String -> Int
f x = read x
```

Next: Declarative Programming.

Acknowledgments

I’d like to thank Gershom Bazerman for checking my math and logic, and André van Meulebrouck, who has been volunteering his editing help.
Follow @BartoszMilewski

April 4, 2015

Orange Mazurka

Posted by Bartosz Milewski under Cooking
[3] Comments

This is the traditional Polish orange mazurka I make every year for Easter.

The Filling

Ingredients for the filling

The filling is homemade orange marmalade:

2 large oranges
2 lemons
sugar, 400g
water, 150 ml
slivered almonds, 100g

Grating whole lemons

Grating whole oranges

You grate lemons and oranges whole, including the pith — it gives the marmalade a bit of a bitter taste. Try to remove the pits, though.

Grated citrus fruit + sugar + water

Cooking the orange marmalade

Cook oranges and lemons with sugar and water for about 45 min, stirring occasionally, until it thickens. Take into account that it will get denser after it cools down.

Adding slivered almonds

Add slivered almonds at the end.

The Crust

The crust is very light and crumbly. It’s a version of pâte sucrée made with cooked egg yolks and no water. (The pictures show double the recipe, which is what I often do. In that case, the marmalade recipe should be doubled.)