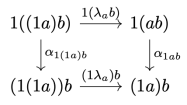This post is based on the talk I gave at Functional Conf 2022. There is a video recording of this talk.
Disclaimers
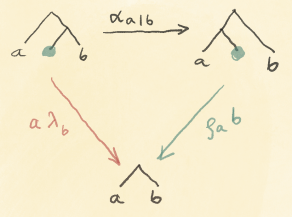
Data types may contain secret information. Some of it can be extracted, some is hidden forever. We’re going to get to the bottom of this conspiracy.
No data types were harmed while extracting their secrets.
No coercion was used to make them talk.
We’re talking, of course, about unsafeCoerce, which should never be used.
Implementation hiding
The implementation of a function, even if it’s available for inspection by a programmer, is hidden from the program itself.
What is this function, with the suggestive name double, hiding inside?
Best guess: It’s hiding 2. It’s probably implemented as:
double x = 2 * x
How would we go about extracting this hidden value? We can just call it with the unit of multiplication:
double 1
> 2
Is it possible that it’s implemented differently (assuming that we’ve already checked it for all values of the argument)? Of course! Maybe it’s adding one, multiplying by two, and then subtracting two. But whatever the actual implementation is, it must be equivalent to multiplication by two. We say that the implementaion is isomorphic to multiplying by two.
Functors
Functor is a data type that hides things of type a. Being a functor means that it’s possible to modify its contents using a function. That is, if we’re given a function a->b and a functorful of a‘s, we can create a functorful of b‘s. In Haskell we define the Functor class as a type constructor equipped with the method fmap:
class Functor f where
fmap :: (a -> b) -> f a -> f b
A standard example of a functor is a list of a‘s. The implementation of fmap applies a function g to all its elements:
instance Functor [] where
fmap g [] = []
fmap g (a : as) = (g a) : fmap g as
Saying that something is a functor doesn’t guarantee that it actually “contains” values of type a. But most data structures that are functors will have some means of getting at their contents. When they do, you can verify that they change their contents after applying fmap. But there are some sneaky functors.
For instance Maybe a tells us: Maybe I have an a, maybe I don’t. But if I have it, fmap will change it to a b.
instance Functor Maybe where
fmap g Empty = Empty
fmap g (Just a) = Just (g a)
A function that produces values of type a is also a functor. A function e->a tells us: I’ll produce a value of type a if you ask nicely (that is call me with a value of type e). Given a producer of a‘s, you can change it to a producer of b‘s by post-composing it with a function g :: a -> b:
instance Functor ((->) e) where
fmap g f = g . f
Then there is the trickiest of them all, the IO functor. IO a tells us: Trust me, I have an a, but there’s no way I could tell you what it is. (Unless, that is, you peek at the screen or open the file to which the output is redirected.)
Continuations
A continuation is telling us: Don’t call us, we’ll call you. Instead of providing the value of type a directly, it asks you to give it a handler, a function that consumes an a and returns the result of the type of your choice:
type Cont a = forall r. (a -> r) -> r
You’d suspect that a continuation either hides a value of type a or has the means to produce it on demand. You can actually extract this value by calling the continuation with an identity function:
runCont :: Cont a -> a
runCont k = k id
In fact Cont a is for all intents and purposes equivalent to a–it’s isomorphic to it. Indeed, given a value of type a you can produce a continuation as a closure:
mkCont :: a -> Cont a
mkCont a = \k -> k a
The two functions, runCont and mkCont are the inverse of each other thus establishing the isomorphism Cont a ~ a.
The Yoneda Lemma
Here’s a variation on the theme of continuations. Just like a continuation, this function takes a handler of a‘s, but instead of producing an x, it produces a whole functorful of x‘s:
type Yo f a = forall x. (a -> x) -> f x
Just like a continuation was secretly hiding a value of the type a, this data type is hiding a whole functorful of a‘s. We can easily retrieve this functorful by using the identity function as the handler:
runYo :: Functor f => Yo f a -> f a
runYo g = g id
Conversely, given a functorful of a‘s we can reconstruct Yo f a by defining a closure that fmap‘s the handler over it:
mkYo :: Functor f => f a -> Yo f a
mkYo fa = \g -> fmap g fa
Again, the two functions, runYo and mkYo are the inverse of each other thus establishing a very important isomorphism called the Yoneda lemma:
Yo f a ~ f a
Both continuations and the Yoneda lemma are defined as polymorphic functions. The forall x in their definition means that they use the same formula for all types (this is called parametric polymorphism). A function that works for any type cannot make any assumptions about the properties of that type. All it can do is to look at how this type is packaged: Is it passed inside a list, a function, or something else. In other words, it can use the information about the form in which the polymorphic argument is passed.
Existential Types
One cannot speak of existential types without mentioning Jean-Paul Sartre.

An existential data type says: There exists a type, but I’m not telling you what it is. Actually, the type has been known at the time of construction, but then all its traces have been erased. This is only possible if the data constructor is itself polymorphic. It accepts any type and then immediately forgets what it was.
Here’s an extreme example: an existential black hole. Whatever falls into it (through the constructor BH) can never escape.
data BlackHole = forall a. BH a
Even a photon can’t escape a black hole:
bh :: BlackHole
bh = BH "Photon"
We are familiar with data types whose constructors can be undone–for instance using pattern matching. In type theory we define types by providing introduction and elimination rules. These rules tell us how to construct and how to deconstruct types.
But existential types erase the type of the argument that was passed to the (polymorphic) constructor so they cannot be deconstructed. However, not all is lost. In physics, we have Hawking radiation escaping a black hole. In programming, even if we can’t peek at the existential type, we can extract some information about the structure surrounding it.
Here’s an example: We know we have a list, but of what?
data SomeList = forall a. SomeL [a]
It turns out that to undo a polymorphic constructor we can use a polymorphic function. We have at our disposal functions that act on lists of arbitrary type, for instance length:
length :: forall a. [a] -> Int
The use of a polymorphic function to “undo” a polymorphic constructor doesn’t expose the existential type:
len :: SomeList -> Int
len (SomeL as) = length as
Indeed, this works:
someL :: SomeList
someL = SomeL [1..10]
> len someL
> 10
Extracting the tail of a list is also a polymorphic function. We can use it on SomeList without exposing the type a:
trim :: SomeList -> SomeList
trim (SomeL []) = SomeL []
trim (SomeL (a: as)) = SomeL as
Here, the tail of the (non-empty) list is immediately stashed inside SomeList, thus hiding the type a.
But this will not compile, because it would expose a:
bad :: SomeList -> a
bad (SomeL as) = head as
Producer/Consumer
Existential types are often defined using producer/consumer pairs. The producer is able to produce values of the hidden type, and the consumer can consume them. The role of the client of the existential type is to activate the producer (e.g., by providing some input) and passing the result (without looking at it) directly to the consumer.
Here’s a simple example. The producer is just a value of the hidden type a, and the consumer is a function consuming this type:
data Hide b = forall a. Hide a (a -> b)
All the client can do is to match the consumer with the producer:
unHide :: Hide b -> b
unHide (Hide a f) = f a
This is how you can use this existential type. Here, Int is the visible type, and Char is hidden:
secret :: Hide Int
secret = Hide 'a' (ord)
The function ord is the consumer that turns the character into its ASCII code:
> unHide secret
> 97
Co-Yoneda Lemma
There is a duality between polymorphic types and existential types. It’s rooted in the duality between universal quantifiers (for all, 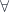 ) and existential quantifiers (there exists,
) and existential quantifiers (there exists, 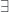 ).
).
The Yoneda lemma is a statement about polymorphic functions. Its dual, the co-Yoneda lemma, is a statement about existential types. Consider the following type that combines the producer of x‘s (a functorful of x‘s) with the consumer (a function that transforms x‘s to a‘s):
data CoYo f a = forall x. CoYo (f x) (x -> a)
What does this data type secretly encode? The only thing the client of CoYo can do is to apply the consumer to the producer. Since the producer has the form of a functor, the application proceeds through fmap:
unCoYo :: Functor f => CoYo f a -> f a
unCoYo (CoYo fx g) = fmap g fx
The result is a functorful of a‘s. Conversely, given a functorful of a‘s, we can form a CoYo by matching it with the identity function:
mkCoYo :: Functor f => f a -> CoYo f a
mkCoYo fa = CoYo fa id
This pair of unCoYo and mkCoYo, one the inverse of the other, witness the isomorphism
CoYo f a ~ f a
In other words, CoYo f a is secretly hiding a functorful of a‘s.
Contravariant Consumers
The informal terms producer and consumer, can be given more rigorous meaning. A producer is a data type that behaves like a functor. A functor is equipped with fmap, which lets you turn a producer of a‘s to a producer of b‘s using a function a->b.
Conversely, to turn a consumer of a‘s to a consumer of b‘s you need a function that goes in the opposite direction, b->a. This idea is encoded in the definition of a contravariant functor:
class Contravariant f where
contramap :: (b -> a) -> f a -> f b
There is also a contravariant version of the co-Yoneda lemma, which reverses the roles of a producer and a consumer:
data CoYo' f a = forall x. CoYo' (f x) (a -> x)
Here, f is a contravariant functor, so f x is a consumer of x‘s. It is matched with the producer of x‘s, a function a->x.
As before, we can establish an isomorphism
CoYo' f a ~ f a
by defining a pair of functions:
unCoYo' :: Contravariant f => CoYo' f a -> f a
unCoYo' (CoYo' fx g) = contramap g fx
mkCoYo' :: Contravariant f => f a -> CoYo' f a
mkCoYo' fa = CoYo' fa id
Existential Lens
A lens abstracts a device for focusing on a part of a larger data structure. In functional programming we deal with immutable data, so in order to modify something, we have to decompose the larger structure into the focus (the part we’re modifying) and the residue (the rest). We can then recreate a modified data structure by combining the new focus with the old residue. The important observation is that we don’t care what the exact type of the residue is. This description translates directly into the following definition:
data Lens' s a =
forall c. Lens' (s -> (c, a)) ((c, a) -> s)
Here, s is the type of the larger data structure, a is the type of the focus, and the existentially hidden c is the type of the residue. A lens is constructed from a pair of functions, the first decomposing s and the second recomposing it.

Given a lens, we can construct two functions that don’t expose the type of the residue. The first is called get. It extracts the focus:
toGet :: Lens' s a -> (s -> a)
toGet (Lens' frm to) = snd . frm
The second, called set replaces the focus with the new value:
toSet :: Lens' s a -> (s -> a -> s)
toSet (Lens' frm to) = \s a -> to (fst (frm s), a)
Notice that access to residue not possible. The following will not compile:
bad :: Lens' s a -> (s -> c)
bad (Lens' frm to) = fst . frm
But how do we know that a pair of a getter and a setter is exactly what’s hidden in the existential definition of a lens? To show this we have to use the co-Yoneda lemma. First, we have to identify the producer and the consumer of c in our existential definition. To do that, notice that a function returning a pair (c, a) is equivalent to a pair of functions, one returning c and another returning a. We can thus rewrite the definition of a lens as a triple of functions:
data Lens' s a =
forall c. Lens' (s -> c) (s -> a) ((c, a) -> s)
The first function is the producer of c‘s, so the rest will define a consumer. Recall the contravariant version of the co-Yoneda lemma:
data CoYo' f s = forall c. CoYo' (f c) (s -> c)
We can define the contravariant functor that is the consumer of c‘s and use it in our definition of a lens. This functor is parameterized by two additional types s and a:
data F s a c = F (s -> a) ((c, a) -> s)
This lets us rewrite the lens using the co-Yoneda representation, with f replaced by (partially applied) F s a:
type Lens' s a = CoYo' (F s a) s
We can now use the isomorphism CoYo' f s ~ f s. Plugging in the definition of F, we get:
Lens' s a ~ CoYo' (F s a) s
CoYo' (F s a) s ~ F s a s
F s a s ~ (s -> a) ((s, a) -> s)
We recognize the two functions as the getter and the setter. Thus the existential representation of the lens is indeed isomorphic to the getter/setter pair.
Type-Changing Lens
The simple lens we’ve seen so far lets us replace the focus with a new value of the same type. But in general the new focus could be of a different type. In that case the type of the whole thing will change as well. A type-changing lens thus has the same decomposition function, but a different recomposition function:
data Lens s t a b =
forall c. Lens (s -> (c, a)) ((c, b) -> t)
As before, this lens is isomorphic to a get/set pair, where get extracts an a:
toGet :: Lens s t a b -> (s -> a)
toGet (Lens frm to) = snd . frm
and set replaces the focus with a new value of type b to produce a t:
toSet :: Lens s t a b -> (s -> b -> t)
toSet (Lens frm to) = \s b -> to (fst (frm s), b)
Other Optics
The advantage of the existential representation of lenses is that it easily generalizes to other optics. The idea is that a lens decomposes a data structure into a pair of types (c, a); and a pair is a product type, symbolically 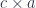
data Lens s t a b =
forall c. Lens (s -> (c, a))
((c, b) -> t)
A prism does the same for the sum data type. A sum  is written as
is written as Either c a in Haskell. We have:
data Prism s t a b =
forall c. Prism (s -> Either c a)
(Either c b -> t)
We can also combine sum and product in what is called an affine type 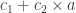 . The resulting optic has two possible residues,
. The resulting optic has two possible residues, c1 and c2:
data Affine s t a b =
forall c1 c2. Affine (s -> Either c1 (c2, a))
(Either c1 (c2, b) -> t)
The list of optics goes on and on.
Profunctors
A producer can be combined with a consumer in a single data structure called a profunctor. A profunctor is parameterized by two types; that is p a b is a consumer of a‘s and a producer of b‘s. We can turn a consumer of a‘s and a producer of b‘s to a consumer of s‘s and a producer of t‘s using a pair of functions, the first of which goes in the opposite direction:
class Profunctor p where
dimap :: (s -> a) -> (b -> t) -> p a b -> p s t
The standard example of a profunctor is the function type p a b = a -> b. Indeed, we can define dimap for it by precomposing it with one function and postcomposing it with another:
instance Profunctor (->) where
dimap in out pab = out . pab . in
Profunctor Optics
We’ve seen functions that were polymorphic in types. But polymorphism is not restricted to types. Here’s a definition of a function that is polymorphic in profunctors:
type Iso s t a b = forall p. Profunctor p =>
p a b -> p s t
This function says: Give me any producer of b‘s that consumes a‘s and I’ll turn it into a producer of t‘s that consumes s‘s. Since it doesn’t know anything else about its argument, the only thing this function can do is to apply dimap to it. But dimap requires a pair of functions, so this profunctor-polymorphic function must be hiding such a pair:
s -> a
b -> t
Indeed, given such a pair, we can reconstruct it’s implementation:
mkIso :: (s -> a) -> (b -> t) -> Iso s t a b
mkIso g h = \p -> dimap g h p
All other optics have their corresponding implementation as profunctor-polymorphic functions. The main advantage of these representations is that they can be composed using simple function composition.
Main Takeaways
- Producers and consumers correspond to covariant and contravariant functors
- Existential types are dual to polymorphic types
- Existential optics combine producers with consumers in one package
- In such optics, producers decompose, and consumers recompose data
- Functions can be polymorphic with respect to types, functors, or profunctors
:
is an object of
.
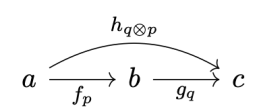
.
is not strict, the parametric composition and identity laws are not strict either. They are satisfied up to associators and unitors of
. A category with lax composition and identity laws is called a bicategory. The 2-cells in a parametric bicategory are called reparameterizations.
is a category in which we define an action of a monoidal category
:
and
. The first constructs parametric morphisms from
to
as
, and the second as
.
construction can be extended to optics, where we’re dealing with pairs of objects from the underlying category (or categories, in the case of mixed optics). The parameterized optic is defined as the following coend:
are objects of some monoidal category
, and the parameters
come from another monoidal category
.
in
to the pair of objects
also in
, parameterized by a pair
in
and a pair
from
.
for the category
, and bold letters for pairs of objects and (twisted) pairs of morphisms. For instance,
is a member of the hom-set
represented by a pair
.
to denote the monoidal action of
on
:
.
bicategory. The composition is a mapping:
and the second by
:
, as long as the two monoidal actions commute, that is, if we have:
,
, and
.
and
. Associativity and identity laws are satisfied modulo the associators and the unitors.
is monoidal, the
bicategory is also monoidal, with the obvious point-wise parallel composition of pre-optics.
to
must give the same result.
.
to be the trivial one-object monoidal category, we get a version of (double-) Tambara modules. If we then take the coend,
, we get regular Tambara modules.
, we can define a mapping
from the triple:
by
and rearranging the actions using their commutativity.
, we map:
can be expressed using triple Tambara modules. An optic:
and get an arbitrary pre-optic.