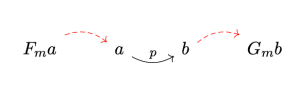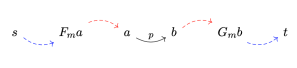Programming

Archived Posts from this Category

January 4, 2025

Legalizing Comonad Composition

Posted by Bartosz Milewski under Category Theory, Haskell, Programming | Tags: Category Theory, Comonad, Game of Life, Haskell |
[7] Comments

The yearly Advent of Code is always a source of interesting coding challenges. You can often solve them the easy way, or spend days trying to solve them “the right way.” I personally prefer the latter. This year I decided to do some yak shaving with a puzzle that involved looking for patterns in a grid. The pattern was the string XMAS, and it could start at any location and go in any direction whatsoever.

My immediate impulse was to elevate the grid to a comonad. The idea is that a comonad describes a data structure in which every location is a center of some neighborhood, and it lets you apply an algorithm to all neighborhoods in one fell swoop. Common examples of comonads are infinite streams and infinite grids.

Why would anyone use an infinite grid to solve a problem on a finite grid? Imagine you’re walking through a neighborhood. At every step you may hit the boundary of a grid. So a function that retrieves the current state is allowed to fail. You may implement it as returning a Maybe value. So why not pre-fill the infinite grid with Maybe values, padding it with Nothing outside of bounds. This might sound crazy, but in a lazy language it makes perfect sense to trade code for data.

I won’t bore you with the details, they are available at my GitHub repository. Instead, I will discuss a similar program, one that I worked out some time ago, but wasn’t satisfied with the solution: the famous Conway’s Game of Life. This one actually uses an infinite grid, and I did implement it previously using a comonad. But this time I was more ambitious: I wanted to generate this two-dimensional comonad by composing a pair of one-dimensional ones.

The idea is simple. Each row of the grid is an infinite bidirectional stream. Since it has a specific “current position,” we’ll call it a cursor. Such a cursor can be easily made into a comonad. You can extract the current value; and you can duplicate a cursor by creating a cursor of cursors, each shifted by the appropriate offset (increasing in one direction, decreasing in the other).

A two-dimensional grid can then be implemented as a cursor of cursors–the inner one extending horizontally, and the outer one vertically.

It should be a piece of cake to define a comonad instance for it: extract should be a composition of (extract . extract) and duplicate a composition of (duplicate . fmap duplicate), right? It typechecks, so it must be right. But, just in case, like every good Haskell programmer, I decided to check the comonad laws. There are three of them:

extract . duplicate = id
fmap extract . duplicate = id
duplicate . duplicate = fmap duplicate . duplicate

And they failed! I must have done something illegal, but what?

In cases like this, it’s best to turn to basics–which means category theory. Compared to Haskell, category theory is much less verbose. A comonad is a functor $W$ equipped with two natural transformations:

$\varepsilon \colon W \to \text{Id}$

$\delta \colon W \to W \circ W$

In Haskell, we write the components of these transformations as:

extract :: w a -> a
duplicate :: w a -> w (w a)

The comonad laws are illustrated by the following commuting diagrams. Here are the two counit laws:

and one associativity law:

These are the same laws we’ve seen above, but the categorical notation makes them look more symmetric.

So the problem is: Given a comonad $W$ , is the composition $W \circ W$ also a comonad? Can we implement the two natural transformations for it?

$\varepsilon_c \colon W \circ W \to \text{Id}$

$\delta_c \colon W \circ W \to W \circ W \circ W \circ W$

The straightforward implementation would be:

$W \circ W \xrightarrow{\varepsilon \circ W} W \xrightarrow{\varepsilon} \text{Id}$

corresponding to (extract . extract), and:

$W \circ W \xrightarrow{W \circ \delta} W \circ W \circ W \xrightarrow{\delta \circ W \circ W} W \circ W \circ W \circ W$

corresponding to (duplicate . fmap duplicate).

To see why this doesn’t work, let’s ask a more general question: When is a composition of two comonads, say $W_2 \circ W_1$ , again a comonad? We can easily define a counit:

$W_2 \circ W_1 \xrightarrow{\varepsilon_2 \circ W_1} W \xrightarrow{\varepsilon_1} \text{Id}$

The comultiplication, though, is tricky:

$W_2 \circ W_1 \xrightarrow{W_2 \circ \delta_1} W_2 \circ W_1 \circ W_1 \xrightarrow{\delta_2 \circ W} W_2 \circ W_2 \circ W_1 \circ W_1$

Do you see the problem? The result is $W_2^2 \circ W_1^2$ but it should be $(W_2 \circ W_1)^2$ . To make it a comonad, we have to be able to push $W_2$ through $W_1$ in the middle. We need $W_2$ to distribute over $W_1$ through a natural transformation:

$\lambda \colon W_2 \circ W_1 \to W_1 \circ W_2$

But isn’t that only relevant when we compose two different comonads–surely any functor distributes over itself! And there’s the rub: Not every comonad distributes over itself. Because a distributive comonad must preserve the comonad laws. In particular, to restore the the counit law we need this diagram to commute:

and for the comultiplication law, we require:

Even if the two comonad are the same, the counit condition is still non-trivial:

The two whiskerings of $\varepsilon$ are in general not equal. All we can get from the original comonad laws is that they are only equal when applied to the result of comultiplication:

$(\varepsilon \circ W) \cdot \delta = (W \circ \varepsilon) \cdot \delta$ .

Equipped with the distributive mapping $\lambda$ we can complete our definition of comultiplication for a composition of two comonads:

$W_2 \circ W_1 \xrightarrow{W_2 \circ \delta_1} W_2 \circ W_1^2 \xrightarrow{\delta_2 \circ W} W_2^2 \circ W_1^2 \xrightarrow{W_2 \circ \lambda \circ W_1} (W_2 \circ W_1)^2$

Going back to our Haskell code, we need to impose the distributivity condition on our comonad. There is a type class for it defined in Data.Distributive:

class Functor w => Distributive w where
  distribute :: Functor f => f (w a) -> w (f a)

Thus the general formula for composing two comonads is:

instance (Comonad w2, Comonad w1, Distributive w1) => 
  Comonad (Compose w2 w1) where
    extract = extract . extract . getCompose
    duplicate = fmap Compose . Compose .
                fmap distribute . duplicate . fmap duplicate .
                getCompose

In particular, it works for composing a comonad with itself, as long as the comonad distributes over itself.

Equipped with these new tools, let’s go back to implementing a two-dimensional infinite grid. We start with an infinite stream:

data Stream a = (:>) { headS :: a
                     , tailS :: Stream a}
  deriving Functor

infixr 5 :>

What does it mean for a stream to be distributive? It means that we can transpose a “matrix” whose rows are streams. The functor f is used to organize these rows. It could, for instance, be a list functor, in which case you’d have a list of (infinite) streams.

  [   1 :>   2 :>   3 .. 
  ,  10 :>  20 :>  30 ..
  , 100 :> 200 :> 300 .. 
  ]

Transposing a list of streams means creating a stream of lists. The first row is a list of heads of all the streams, the second row is a list of second elements of all the streams, and so on.

  [1, 10, 100] :>
  [2, 20, 200] :>
  [3, 30, 300] :>
  ..

Because streams are infinite, we end up with an infinite stream of lists. For a general functor, we use a recursive formula:

instance Distributive Stream where
    distribute :: Functor f => f (Stream a) -> Stream (f a)
    distribute stms = (headS  stms) :> distribute (tailS  stms)

(Notice that, if we wanted to transpose a list of lists, this procedure would fail. Interestingly, the list monad is not distributive. We really need either fixed size or infinity in the picture.)

We can build a cursor from two streams, one going backward to infinity, and one going forward to infinity. The head of the forward stream will serve as our “current position.”

data Cursor a = Cur { bwStm :: Stream a
                    , fwStm :: Stream a }
  deriving Functor

Because streams are distributive, so are cursors. We just flip them about the diagonal:

instance Distributive Cursor where
    distribute :: Functor f => f (Cursor a) -> Cursor (f a)
    distribute fCur = Cur (distribute (bwStm  fCur)) 
                          (distribute (fwStm  fCur))

A cursor is also a comonad:

instance Comonad Cursor where
  extract (Cur _ (a :> _)) = a
  duplicate bi = Cur (iterateS moveBwd (moveBwd bi)) 
                     (iterateS moveFwd bi)

duplicate creates a cursor of cursors that are progressively shifted backward and forward. The forward shift is implemented as:

moveFwd :: Cursor a -> Cursor a
moveFwd (Cur bw (a :> as)) = Cur (a :> bw) as

and similarly for the backward shift.

Finally, the grid is defined as a cursor of cursors:

type Grid a = Compose Cursor Cursor a

And because Cursor is a distributive comonad, Grid is automatically a lawful comonad. We can now use the comonadic extend to advance the state of the whole grid:

generations :: Grid Cell -> [Grid Cell]
generations = iterate $ extend nextGen

using a local function:

nextGen :: Grid Cell -> Cell
nextGen grid
  | cnt == 3 = Full
  | cnt == 2 = extract grid
  | otherwise = Empty
  where
      cnt = countNeighbors grid

You can find the full implementation of the Game of Life and the solution of the Advent of Code puzzle, both using comonad composition, on my GitHub.

March 24, 2024

Neural Networks, Pre-lenses, and Triple Tambara Modules, Part II

Posted by Bartosz Milewski under Category Theory, Lens, Neural Networks, Programming | Tags: AI, Category Theory, Lens, Neural Networks, Optics, Profunctors, Tambara Modules |
1 Comment

I will now provide the categorical foundation of the Haskell implementation from the previous post. A PDF version that contains both parts is also available.

The Para Construction

There’s been a lot of interest in categorical foundations of deep learning. The basic idea is that of a parametric category, in which morphisms are parameterized by objects from a monoidal category $\mathcal P$ :

Screenshot 2024-03-24 at 15.00.20
Here, $p$ is an object of $\mathcal P$ .

When two such morphisms are composed, the result is parameterized by the tensor product of the parameters.

Screenshot 2024-03-24 at 15.00.34

An identity morphism is parameterized by the monoidal unit $I$ .

If the monoidal category $\mathcal P$ is not strict, the parametric composition and identity laws are not strict either. They are satisfied up to associators and unitors of $\mathcal P$ . A category with lax composition and identity laws is called a bicategory. The 2-cells in a parametric bicategory are called reparameterizations.

Of particular interest are parameterized bicategories that are built on top of actegories. An actegory $\mathcal C$ is a category in which we define an action of a monoidal category $\mathcal P$ :

$\bullet \colon \mathcal P \times \mathcal C \to C$

satisfying some obvious coherency conditions (unit and composition):

$I \bullet c \cong c$

$p \bullet (q \bullet c) \cong (p \otimes q) \bullet c$

There are two basic constructions of a parametric category on top of an actegory called $\mathbf{Para}$ and $\mathbf{coPara}$ . The first constructs parametric morphisms from $a$ to $b$ as $f_p = p \bullet a \to b$ , and the second as $g_p = a \to p \bullet b$ .

Parametric Optics

The $\mathbf{Para}$ construction can be extended to optics, where we’re dealing with pairs of objects from the underlying category (or categories, in the case of mixed optics). The parameterized optic is defined as the following coend:

$O \langle a, da \rangle \langle p, dp \rangle \langle s, ds \rangle = \int^{m} \mathcal C (p \bullet s, m \bullet a) \times \mathcal C (m \bullet da, dp \bullet ds)$

where the residues $m$ are objects of some monoidal category $\mathcal M$ , and the parameters $\langle p, dp \rangle$ come from another monoidal category $\mathcal P$ .

In Haskell, this is exactly the existential lens:

data ExLens a da p dp s ds = 
  forall m . ExLens ((p, s)  -> (m, a))  
                    ((m, da) -> (dp, ds))

There is, however, a more general bicategory of pre-optics, which underlies existential optics. In it, both the parameters and the residues are treated symmetrically.

The PreLens Bicategory

Pre-optics break the feedback loop in which the residues from the forward pass are fed back to the backward pass. We get the following formula:

$\begin{aligned}O & \langle a, da \rangle \langle m, dm \rangle \langle p, dp \rangle \langle s, ds \rangle = \\ &\mathcal C (p \bullet s, m \bullet a) \times \mathcal C (dm \bullet da, dp \bullet ds) \end{aligned}$

We interpret this as a hom-set from a pair of objects $\langle s, ds \rangle$ in $\mathcal C^{op} \times C$ to the pair of objects $\langle a, da \rangle$ also in $\mathcal C^{op} \times C$ , parameterized by a pair $\langle m, dm \rangle$ in $\mathcal M \times \mathcal M^{op}$ and a pair $\langle p, dp \rangle$ from $\mathcal P^{op} \times \mathcal P$ .

To simplify notation, I’ll use the bold $\mathbf C$ for the category $\mathcal C^{op} \times \mathcal C$ , and bold letters for pairs of objects and (twisted) pairs of morphisms. For instance, $\bold f \colon \bold a \to \bold b$ is a member of the hom-set $\mathbf C (\bold a, \bold b)$ represented by a pair $\langle f \colon a' \to a, g \colon b \to b' \rangle$ .

Similarly, I’ll use the notation $\bold m \bullet \bold a$ to denote the monoidal action of $\mathcal M^{op} \times \mathcal M$ on $\mathcal C^{op} \times \mathcal C$ :

$\langle m, dm \rangle \bullet \langle a, da \rangle = \langle m \bullet a, dm \bullet da \rangle$

and the analogous action of $\mathcal P^{op} \times \mathcal P$ .

In this notation, the pre-optic can be simply written as:

$O\; \bold a\, \bold m\, \bold p\, \bold s = \bold C (\bold m \bullet \bold a, \bold p \bullet \bold b)$

and an individual morphism as a triple:

$(\bold m, \bold p, \bold f \colon \bold m \bullet \bold a \to \bold p \bullet \bold b)$

Pre-optics form hom-sets in the $\mathbf{PreLens}$ bicategory. The composition is a mapping:

$\mathbf C (\bold m \bullet \bold b, \bold p \bullet \bold c) \times \mathbf C (\bold n \bullet \bold a, \bold q \bullet \bold b) \to \mathbf C (\bold (\bold m \otimes \bold n) \bullet \bold a, (\bold q \otimes \bold p) \bullet \bold c)$

Indeed, since both monoidal actions are functorial, we can lift the first morphism by $(\bold q \bullet -)$ and the second by $(\bold m \bullet -)$ :

$\mathbf C (\bold m \bullet \bold b, \bold p \bullet \bold c) \times \mathbf C (\bold n \bullet \bold a, \bold q \bullet \bold b) \xrightarrow{(\bold q \bullet) \times (\bold m \bullet)}$

$\mathbf C (\bold q \bullet \bold m \bullet \bold b, \bold q \bullet \bold p \bullet \bold c) \times \mathbf C (\bold m \bullet \bold n \bullet \bold a,\bold m \bullet \bold q \bullet \bold b)$

We can compose these hom-sets in $\mathbf C$ , as long as the two monoidal actions commute, that is, if we have:

$\bold q \bullet \bold m \bullet \bold b \to \bold m \bullet \bold q \bullet \bold b$

for all $\bold q$ , $\bold m$ , and $\bold b$ .
The identity morphism is a triple:

$(\bold 1, \bold 1, \bold{id} )$

parameterized by the unit objects in the monoidal categories $\mathbf M$ and $\mathbf P$ . Associativity and identity laws are satisfied modulo the associators and the unitors.

If the underlying category $\mathcal C$ is monoidal, the $\mathbf{PreOp}$ bicategory is also monoidal, with the obvious point-wise parallel composition of pre-optics.

Triple Tambara Modules

A triple Tambara module is a functor:

$T \colon \mathbf M^{op} \times \mathbf P \times \mathbf C \to \mathbf{Set}$

equipped with two families of natural transformations:

$\alpha \colon T \, \bold m \, \bold p \, \bold a \to T \, (\bold n \otimes \bold m) \, \bold p \, (\bold n \bullet a)$

$\beta \colon T \, \bold m \, \bold p \, (\bold r \bullet \bold a) \to T \, \bold m \, (\bold p \otimes \bold r) \, \bold a$

and some coherence conditions. For instance, the two paths from $T \, \bold m \, \bold p\, (\bold r \bullet \bold a)$ to $T \, (\bold n \otimes \bold m)\, (\bold p \otimes \bold r) \, (\bold n \bullet \bold a)$ must give the same result.

One can also define natural transformations between such functors that preserve the two structures, and define a bicategory of triple Tambara modules $\mathbf{TriTamb}$ .

As a special case, if we chose the category $\mathcal P$ to be the trivial one-object monoidal category, we get a version of (double-) Tambara modules. If we then take the coend, $P \langle a, b \rangle = \int^m T \langle m, m\rangle \langle a, b \rangle$ , we get regular Tambara modules.

Pre-optics themselves are an example of a triple Tambara representation. Indeed, for any fixed $\bold a$ , we can define a mapping $\alpha$ from the triple:

$(\bold m, \bold p, \bold f \colon \bold m \bullet \bold a \to \bold p \bullet \bold b)$

to the triple:

$(\bold n \otimes \bold m, \bold p, \bold f' \colon (\bold n \otimes \bold m) \bullet \bold a \to \bold p \bullet (\bold n \bullet \bold b))$

by lifting of $\bold f$ by $(\bold n \bullet -)$ and rearranging the actions using their commutativity.
Similarly for $\beta$ , we map:

$(\bold m, \bold p, \bold f \colon \bold m \bullet \bold a \to \bold p \bullet (\bold r \bullet \bold b))$

to:

$(\bold m , (\bold p \otimes \bold r), \bold f' \colon \bold m \bullet \bold a \to (\bold p \otimes \bold r) \bullet \bold b)$

Tambara Representation

The main result is that morphisms in $\mathbf {PreOp}$ can be expressed using triple Tambara modules. An optic:

$(\bold m, \bold p, \bold f \colon \bold m \bullet \bold a \to \bold p \bullet \bold b)$

is equivalent to a triple end:

$\int_{\bold r \colon \mathbf P} \int_{\bold n \colon \mathbf M} \int_{T \colon \mathbf{TriTamb}} \mathbf{Set} \big(T \, \bold n \, \bold r \, \bold a, T \, (\bold m \otimes \bold n) \, (\bold r \otimes \bold p) \, \bold b \big)$

Indeed, since pre-optics are themselves triple Tambara modules, we can apply the polymorphic mapping of Tambara modules to the identity optic $(\bold 1, \bold 1, \bold{id} )$ and get an arbitrary pre-optic.

Conversely, given an optic:

$(\bold m, \bold p, \bold f \colon \bold m \bullet \bold a \to \bold p \bullet \bold b)$

we can construct the polymorphic mapping of triple Tambara modules:

$\begin{aligned} & T \, \bold n \, \bold r \, \bold a \xrightarrow{\alpha} T \, (\bold m \otimes \bold n) \, \bold r \, (\bold m \bullet \bold a) \xrightarrow{T \, \bold f} T \, (\bold m \otimes \bold n) \, \bold r \, (\bold p \bullet \bold b) \xrightarrow{\beta} \\ & T \, (\bold m \otimes \bold n) \, (\bold r \otimes \bold p) \, \bold b \end{aligned}$

Bibliography

Brendan Fong, Michael Johnson, Lenses and Learners,
Brendan Fong, David Spivak, Rémy Tuyéras, Backprop as Functor: A compositional perspective on supervised learning, 34th Annual ACM/IEEE Symposium on Logic in Computer Science (LICS) 2019, pp. 1-13, 2019.
G.S.H. Cruttwell, Bruno Gavranović, Neil Ghani, Paul Wilson, Fabio Zanasi, Categorical Foundations of Gradient-Based Learning
Bruno Gavranović, Compositional Deep Learning
Bruno Gavranović, Fundamental Components of Deep Learning, PhD Thesis. 2024

March 22, 2024

Neural Networks, Pre-Lenses, and Triple Tambara Modules

Posted by Bartosz Milewski under Programming | Tags: AI, artificial-intelligence, deep-learning, Lens, machine-learning, Neural Networks, Optics, Profunctors, Tambara Modules |
1 Comment

Introduction

Neural networks are an example of composable systems, so it’s no surprise that they can be modeled in category theory, which is the ultimate science of composition. Moreover, the categorical ideas behind neural networks can be immediately implemented and tested in a programming language. In this post I will present the Haskell implementation of parametric lenses, generalize them to pre-lenses and introduce their profunctor representation. Using the profunctor representation I will build a working multi-layer perceptron.

In the second part of this post I will introduce the bicategory $\mathbf{PreLens}$ of pre-lenses and the bicategory of triple Tambara profunctors and show how they related to pre-lenses.

Complete Haskell implementation is available on gitHub, where you can also find the PDF version of this post, complete with the categorical picture.

Haskell Implementation

Every component of a neural network can be thought of as a system that transform input to output, and whose action depends on some parameters. In the language of neural networsks, this is called the forward pass. It takes a bunch of parameters p, combines it with the input s, and produces the output a. It can be described by a Haskell function:

fwd :: (p, s) -> a

But the real power of neural networks is in their ability to learn from mistakes. If we don’t like the output of the network, we can nudge it towards a better solution. If we want to nudge the output by some da, what change dp to the parameters should we make? The backward pass partitions the blame for the perceived error in direct proportion to the impact each parameter had on the result.

Because neural networks are composed of layers of neurons, each with their own sets or parameters, we might also ask the question: What change ds to this layer’s inputs (which are the outputs of the previous layer) should we make to improve the result? We could then back-propagate this information to the previous layer and let it adjust its own parameters. The backward pass can be described by another Haskell function:

bwd :: (p, s, da) -> (dp, ds)

The combination of these two functions forms a parametric lens:

data PLens a da p dp s ds = 
  PLens { fwd :: (p, s) -> a
        , bwd :: (p, s, da) -> (dp, ds) }

In this representation it’s not immediately obvious how to compose parametric lenses, so I’m going to present a variety of other representations that may be more convenient in some applications.

Existential Parametric Lens

Notice that the backward pass re-uses the arguments (p, s) of the forward pass. Although some information from the forward pass is needed for the backward pass, it’s not always clear that all of it is required. It makes more sense for the forward pass to produce some kind of a care package to be delivered to the backward pass. In the simplest case, this package would just be the pair (p, s). But from the perspective of the user of the lens, the exact type of this package is an internal implementation detail, so we might as well hide it as an existential type m. We thus arrive at a more symmetric representation:

data ExLens a da p dp s ds = 
  forall m . ExLens ((p, s)  -> (m, a))  
                    ((m, da) -> (dp, ds))

The type m is often called the residue of the lens.

These existential lenses can be composed in series. The result of the composition is parameterized by the product (a tuple) of the original parameters. We’ll see it more clearly in the next section.

But since the product of types is associative only up to isomorphism, the composition of parametric lenses is associative only up to isomorphism.

There is also an identity lens:

identityLens :: ExLens a da () () a da
identityLens = ExLens id id

but, again, the categorical identity laws are satisfied only up to isomorphism. This is why parametric lenses cannot be interpreted as hom-sets in a traditional category. Instead they are part of a bicategory that arises from the $\mathbf{Para}$ construction.

Pre-Lenses

Notice that there is still an asymmetry in the treatment of the parameters and the residues. The parameters are accumulated (tupled) during composition, while the residues are traced over (categorically, an existential type is described by a coend, which is a generalized trace). There is no reason why we shouldn’t accumulate the residues during composition and postpone the taking of the trace untill the very end.

We thus arrive at a fully symmetrical definition of a pre-lens:

data PreLens a da m dm p dp s ds =
  PreLens ((p, s)   -> (m, a))
          ((dm, da) -> (dp, ds))

We now have two separate types: m describing the residue, and dm describing the change of the residue.

Screenshot 2024-03-22 at 12.19.58

If all we need at the end is to trace over the residues, we’ll identify the two types.

Notice that the role of parameters and residues is reversed between the forward and the backward pass. The forward pass, given the parameters and the input, produces the output plus the residue. The backward pass answers the question: How should we nudge the parameters and the inputs (dp, ds) if we want the residues and the outputs to change by (dm, da). In neural networks this will be calculated using gradient descent.

The composition of pre-lenses accumulates both the parameters and the residues into tuples:

preCompose ::
    PreLens a' da' m dm p dp s ds -> 
    PreLens a da n dn q dq a' da' ->
    PreLens a da (m, n) (dm, dn) (q, p) (dq, dp) s ds
preCompose (PreLens f1 g1) (PreLens f2 g2) = PreLens f3 g3
  where
    f3 = unAssoc . second f2 . assoc . first sym . 
         unAssoc . second f1 . assoc
    g3 = unAssoc . second g1 . assoc . first sym . 
         unAssoc . second g2 . assoc

We use associators and symmetrizers to rearrange various tuples. Notice the separation of forward and backward passes. In particular, the backward pass of the composite lens depends only on backward passes of the composed lenses.

There is also an identity pre-lens:

idPreLens :: PreLens a da () () () () a da
idPreLens = PreLens id id

Pre-lenses thus form a bicategory that combines the $\mathbf{Para}$ and the $\mathbf{coPara}$ constructions in one.

There is also a monoidal structure in this category induced by parallel composition. In parallel composition we tuple the respective inputs and outputs, as well as the parameters and residues, both in the forward and the backward passes.

The existential lens can be obtained from the pre-lens at any time by tracing over the residues:

data ExLens a da p dp s ds = 
  forall m. ExLens (PreLens a da m m p dp s ds)

Notice however that the tracing can be performed after we are done with all the (serial and parallel) compositions. In particular, we could dedicate one pipeline to perform forward passes, gathering both parameters and residues, and then send this data over to another pipeline that performs backward passes. The data is produced and consumed in the LIFO order.

Pre-Neuron

As an example, let’s implement the basic building block of neural networks, the neuron. In what follows, we’ll use the following type synonyms:

type D = Double
type V = [D]

A neuron can be decomposed into three mini-layers. The first layer is the linear transformation, which calculates the scalar product of the input vector and the vector of parameters:

$a = \sum_{i = 1}^n p_i \times s_i$

It also produces the residue which, in this case, consists of the tuple (V, V) of inputs and parameters:

fw :: (V, V) -> ((V, V), D)
fw (p, s) = ((s, p), sumN n $ zipWith (*) p s)

The backward pass has the general signature:

bw :: ((dm, da) -> (dp, ds))

Because we’re eventually going to trace over the residues, we’ll use the same type for dm as for m. And because we are going to do arithmetic over the parameters, we reuse the type of p for the delta dp. Thus the signature of the backward pass is:

bw :: ((V, V), D) -> (V, V)

In the backward pass we’ll encode the gradient descent. The steepest gradient direction and slope is given by the partial derivatives:

$\frac{\partial{ a}}{\partial p_i} = s_i$

$\frac{\partial{ a}}{\partial s_i} = p_i$

We multiply them by the desired change in the output da:

dp = fmap (da *) s
ds = fmap (da *) p

Here’s the resulting lens:

linearL :: Int -> PreLens D D (V, V) (V, V) V V V V
linearL n = PreLens fw bw
  where
    fw :: (V, V) -> ((V, V), D)
    fw (p, s) = ((s, p), sumN n $ zipWith (*) p s)
    bw :: ((V, V), D) -> (V, V)
    bw ((s, p), da) = (fmap (da *) s
                      ,fmap (da *) p)

The linear transformation is followed by a bias, which uses a single number as the parameter, and generates no residue:

biasL :: PreLens D D () () D D D D
biasL = PreLens fw bw 
  where 
    fw :: (D, D) -> ((), D)
    fw (p, s) = ((), p + s)
    -- da/dp = 1, da/ds = 1
    bw :: ((), D) -> (D, D)
    bw (_, da) = (da, da)

Finally, we implement the non-linear activation layer using the tanh function:

activL :: PreLens D D D D () () D D
activL = PreLens fw bw
  where
    fw (_, s) = (s, tanh s)
    -- da/ds = 1 + (tanh s)^2
    bw (s, da)= ((), da * (1 - (tanh s)^2))

A neuron with $m$ inputs is a composition of the three components, modulo some monoidal rearrangements:

neuronL :: Int -> 
    PreLens D D ((V, V), D) ((V, V), D) Para Para V V

neuronL mIn = PreLens f' b'
  where 
    PreLens f b = 
      preCompose (preCompose (linearL mIn) biasL) activL
    f' :: (Para, V) -> (((V, V), D), D)
    f' (Para bi wt, s) = let (((vv, ()), d), a) = 
        f (((), (bi, wt)), s)
                         in ((vv, d), a)
    b' :: (((V, V), D), D) -> (Para, V)
    b' ((vv, d), da) = let (((), (d', w')), ds) = 
        b (((vv, ()), d), da)
                       in (Para d' w', ds)

The parameters for the neuron can be conveniently packaged into one data structure:

data Para = Para { bias   :: D
                 , weight :: V }

mkPara (b, v) = Para b v
unPara p = (bias p, weight p)

Using parallel composition, we can create whole layers of neurons, and then use sequential composition to model multi-layer neural networks. The loss function that compares the actual output with the expected output can also be implemented as a lens. We’ll perform this construction later using the profunctor representation.

Tambara Modules

As a rule, all optics that have an existential representation also have some kind of profunctor representation. The advantage of profunctor representations is that they are functions, and they compose using function composition.

Lenses, in particular, have a representation using a special category of profunctors called Tambara modules. A vanilla Tambara module is a profunctor p equipped with a family of transformations. It can be implemented as a Haskell class:

class  Profunctor p => Tambara p where
  alpha :: forall a da m. p a da -> p (m, a) (m, da)

The vanilla lens is then represented by the following profunctor-polymorphic function:

type Lens a da s ds = forall p. Tambara p => p a da -> p s ds

A similar representation can be constructed for pre-lenses. A pre-lens, however, has additional dependency on parameters and residues, so the analog of a Tambara module must also be parameterized by those. We need, therefore, a more complex type constructor t that takes six arguments:

t m dm p dp s ds

This is supposed to be a profunctor in three pairs of arguments, s ds, p dp, and dm m. Pro-functoriality in the first two pairs is implemented as two functions, diampS and dimapP. The inverted order in dm m means that t is covariant in m and contravariant in dm, as seen in the unusual type signature of dimapM:

dimapM  :: (m -> m') -> (dm' -> dm) -> 
  t m dm p dp s ds -> t m' dm' p  dp  s  ds

To generalize Tambara modules we first observe that the pre-lens now has two independent residues, m and dm, and the two should transform separately. Also, the composition of pre-lenses accumulates (through tupling) both the residues and the parameters, so it makes sense to use the additional type arguments to TriProFunctor as accumulators. Thus the generalized Tambara module has two methods, one for accumulating residues, and one for accumulating parameters:

class TriProFunctor t => Trimbara t where
  alpha :: t m dm p dp s ds -> 
           t (m1, m) (dm1, dm) p dp (m1, s) (dm1, ds)
  beta  :: t m dm p dp (p1, s) (dp1, ds) -> 
           t m dm (p, p1) (dp, dp1) s ds

These generalized Tambara modules satisfy some coherency conditions.

One can also define natural transformations that are compatible with the new structures, so that Trimbara modules form a category.

The question arises: can this definition be satisfied by an actual non-trivial TriProFunctor? Fortunately, it turns out that a pre-lens itself is an example of a Trimbara module. Here’s the implementation of alpha for a PreLens:

alpha (PreLens fw bw) = PreLens fw' bw'
  where
    fw' (p, (n, s)) = let (m, a) = fw (p, s)
                      in ((n, m), a)
    bw' ((dn, dm), da) = let (dp, ds) = bw (dm, da)
                         in (dp, (dn, ds))

and this is beta:

beta (PreLens fw bw) = PreLens fw' bw'
  where
    fw' ((p, r), s) = let (m, a) = fw (p, (r, s))
                      in (m, a)
    bw' (dm, da) = let (dp, (dr, ds)) = bw (dm, da)
                   in ((dp, dr), ds)

This result will become important in the next section.

TriLens

Since Trimbara modules form a category, we can define a polymorphic function type (a categorical end) over Trimbara modules . This gives us the (tri-)profunctor representation for a pre-lens:

type TriLens a da m dm p dp s ds =
    forall t. Trimbara t => forall p1 dp1 m1 dm1. 
      t m1 dm1 p1 dp1 a da -> 
      t (m, m1) (dm, dm1) (p1, p) (dp1, dp) s ds

Indeed, given a pre-lens we can construct the requisite mapping of Trimbara modules simply by lifting the two functions (the forward and the backward pass) and sandwiching them between the two Tambara structure maps:

toTamb :: PreLens a da m dm p dp s ds -> 
    TriLens a da m dm p dp s ds
toTamb (PreLens fw bw) = beta . dimapS fw bw . alpha

Conversely, given a mapping between Trimbara modules, we can construct a pre-lens by applying it to the identity pre-lens (modulo some rearrangement of tuples using the monoidal right/left unit laws):

fromTamb :: TriLens a da m dm p dp s ds -> 
    PreLens a da m dm p dp s ds
fromTamb f = dimapM runit unRunit $  
             dimapP unLunit lunit $ 
             f idPreLens

The main advantage of the profunctor representation is that we can now compose two lenses using simple function composition; again, modulo some associators:

triCompose ::
    TriLens b db m dm p dp s ds -> 
    TriLens a da n dn q dq b db ->
    TriLens a da (m, n) (dm, dn) (q, p) (dq, dp) s ds
triCompose f g = dimapP unAssoc assoc . 
                 dimapM unAssoc assoc . 
                 f . g

Parallel composition of TriLenses is also relatively straightforward, although it involves a lot of bookkeeping (see the gitHub implementation).

Training a Neural Network

As a proof of concept, I have implemented and trained a simple 3-layer perceptron.

The starting point is the conversion of the individual components of the neuron from their pre-lens representation to the profunctor representation using toTamb. For instance:

linearT :: Int -> TriLens D D (V, V) (V, V) V V V V
linearT n = toTamb (linearL n)

We get a profunctor representation of a neuron by composing its three components:

neuronT :: Int -> 
  TriLens D D ((V, V), D) ((V, V), D) Para Para V V
neuronT mIn = 
  dimapP (second (unLunit . unPara)) 
         (second (mkPara . lunit)) .
  triCompose (dimapM (first runit) (first unRunit) .
  triCompose (linearT mIn) biasT) activT

With parallel composition of tri-lenses, we can build a layer of neurons of arbitrary width.

layer :: Int -> Int -> 
  TriLens V V [((V, V), D)] [((V, V), D)] [Para] [Para] V V
layer mIn nOut = 
  dimapP (second unRunit) (second runit) .
  dimapM (first lunit) (first unLunit) .
  triCompose (branch nOut) (vecLens nOut (neuronT mIn))

The result is again a tri-lens, and such tri-lenses can be composed in series to create a multi-layer perceptron.

makeMlp :: Int -> [Int] -> 
  TriLens V V -- output
          [[((V, V), D)]] [[((V, V), D)]] -- residues
          [[Para]] [[Para]] -- parameters
          V V -- input

Here, the first integer specifies the number of inputs of each neuron in the first layer. The list [Int] specifies the number of neurons in consecutive layers (which is also the number of inputs of each neuron in the following layer).

The training of a neural network is usually done by feeding it a batch of inputs together with a batch of expected outputs. This can be simply done by arranging multiple perceptrons in parallel and accumulating the parameters for the whole batch.

batchN :: (VSpace dp) => Int -> 
    TriLens  a da m dm p dp s ds -> 
    TriLens [a] [da] [m] [dm] p dp [s] [ds]

To make the accumulation possible, the parameters must form a vector space, hence the constraint VSpace dp.

The whole thing is then capped by a square-distance loss lens that is parameterized by the ground truth values:

lossL :: PreLens D D ([V], [V]) ([V], [V]) [V] [V] [V] [V]
lossL = PreLens fw bw 
  where
    fw (gTruth, s) = 
      ((gTruth, s), sqDist (concat s) (concat gTruth))
    bw ((gTruth, s), da) = (fmap (fmap negate) delta', delta')
      where
        delta' = fmap (fmap (da *)) (zipWith minus s gTruth)

In the next post I will present the categorical version of this construction.

February 7, 2024

Linear Lenses in Haskell

Posted by Bartosz Milewski under Programming | Tags: Category Theory, education, Functional Programming, hinduism, mathematics, Optics, Profunctors, Tambara Modules |
[3] Comments

I always believed that the main problems in designing a programming language were resource management and concurrency–and the two are related. If you can track ownership of resources, you can be sure that no synchronization is needed when there’s a single owner.

I’ve been evangelizing resource management for a long time, first in C++, and then in D (see Appendix 3). I was happy to see it implemented in Rust as ownership types, and I’m happy to see it coming to Haskell as linear types.

Haskell has essentially solved the concurrency and parallelism problems by channeling mutation to dedicated monads, but resource management has always been part of the awkward squad. The main advantage of linear types in Haskell, other than dealing with external resources, is to allow safe mutation and non-GC memory management. This could potentially lead to substantial performance gains.

This post is based on very informative discussions I had with Arnaud Spiwack, who explained to me the work he’d done on linear types and linear lenses, some of it never before documented.

The PDF version of this post together with complete Haskell code is available on GitHub.

Linear types

What is a linear function? The short answer is that a linear function $a \multimap b$ “consumes” its argument exactly once. This is not the whole truth, though, because we also have linear identity $id_a \colon a \multimap a$ , which ostensibly does not consume $a$ . The long answer is that a linear function consumes its argument exactly once if it itself is consumed exactly once, and its result is consumed exactly once.

What remains to define is what it means to be consumed. A function is consumed when it’s applied to its argument. A base value like Int or Char is consumed when it’s evaluated, and an algebraic data type is consumed when it’s pattern-matched and all its matched components are consumed.

For instance, to consume a linear pair (a, b), you pattern-match it and then consume both a and b. To consume Either a b, you pattern-match it and consume the matched component, either a or b, depending on which branch was taken.

As you can see, except for the base values, a linear argument is like a hot potato: you “consume” it by passing it to somebody else.

So where does the buck stop? This is where the magic happens: Every resource comes with a special primitive that gets rid of it. A file handle gets closed, memory gets deallocated, an array gets frozen, and Frodo throws the ring into the fires of Mount Doom.

To notify the type system that the resource has been destroyed, a linear function will return a value inside the special unrestricted type Ur. When this type is pattern-matched, the original resource is finally destroyed.

For instance, for linear arrays, one such primitive is toList:

$\mathit{toList} \colon \text{Array} \; a \multimap \text{Ur} \, [a]$

In Haskell, we annotate the linear arrows with multiplicity 1:

toList :: Array a %1-> Ur  [a]

Similarly, magic is used to create the resource in the first place. For arrays, this happens inside the primitive fromList.

$\mathit{fromList} \colon [a] \to (\text{Array} \; a \multimap \text{Ur} \; b) \multimap \text{Ur} \; b$

or using Haskell syntax:

fromList :: [a] -> (Array a %1-> Ur b) %1-> Ur b

The kind of resource management I advertised in C++ was scope based. A resource was encapsulated in a smart pointer that was automatically destroyed at scope exit.

With linear types, the role of the scope is played by a user-provided linear function; here, the continuation:

(Array a %1 -> Ur b)

The primitive fromList promises to consume this user-provided function exactly once and to return its unrestricted result. The client is obliged to consume the array exactly once (e.g., by calling toList). This obligation is encoded in the type of the continuation accepted by fromList.

Linear lens: The existential form

A lens abstracts the idea of focusing on a part of a larger data structure. It is used to access or modify its focus. An existential form of a lens consists of two functions: one splitting the source into the focus and the residue; and the other replacing the focus with a new value, and creating a new whole. We don’t care about the actual type of the residue so we keep it as an existential.

The way to think about a linear lens is to consider its source as a resource. The act of splitting it into a focus and a residue is destructive: it consumes its source to produce two new resources. It splits one hot potato s into two hot potatoes: the residue c and the focus a.

Conversely, the part that rebuilds the target t must consume both the residue c and the new focus b.

We end up with the following Haskell implementation:

data LinLensEx a b s t where
  LinLensEx :: (s %1-> (c, a)) -> 
               ((c, b) %1-> t) -> LinLensEx a b s t

A Haskell existential type corresponds to a categorical coend, so the above definition is equivalent to:

$L a b s t = \int^c (s \multimap c \otimes a)\times (c \otimes b \multimap t)$

I use the lollipop notation for the hom-set in a monoidal category with a tensor product $\otimes$ .

The important property of a monoidal category is that its tensor product doesn’t come with a pair of projections; and the unit object is not terminal. In particular, a morphism $s \multimap c \otimes a$ cannot be decomposed into a product of two morphisms $(s \multimap c) \times (s \multimap a)$ .

However, in a closed monoidal category we can curry a mapping out of a tensor product:

$c \otimes b \multimap t \cong c \multimap (b \multimap t)$

We can therefore rewrite the existential lens as:

$L a b s t \cong \int^c (s \multimap c \otimes a)\times (c \multimap (b \multimap t))$

and then apply the co-Yoneda lemma to get:

$s \multimap \big((b \multimap t) \otimes a\big)$

Unlike the case of a standard lens, this form cannot be separated into a get/set pair.

The intuition is that a linear lens lets you consume the object $s$ , but it leaves you with the obligation to consume both the setter $b \multimap t$ and the focus $a$ . You can’t just extract $a$ alone, because that would leave a gaping hole in your object. You have to plug it in with a new object $b$ , and that’s what the setter lets you do.

Here’s the Haskell translation of this formula (conventionally, with the pairs of arguments reversed):

type LinLens s t a b = s %1-> (b %1-> t, a)

The Yoneda shenanigans translate into a pair of Haskell functions. Notice that, just like in the co-Yoneda trick, the existential $c$ is replaced by the linear function $b \multimap t$ .

fromLinLens :: forall s t a b.
  LinLens s t a b -> LinLensEx a b s t
fromLinLens h = LinLensEx f g
  where
    f :: s %1-> (b %1-> t, a)
    f = h
    g :: (b %1-> t, b) %1-> t
    g (set, b) = set b

The inverse mapping is:

toLinLens :: LinLensEx a b s t -> LinLens s t a b
toLinLens (LinLensEx f g) s = 
  case f s of
    (c, a) -> (\b -> g (c, b), a)

Profunctor representation

Every optic comes with a profunctor representation and the linear lens is no exception. Categorically speaking, a profunctor is a functor from the product category $\mathcal C^{op} \times \mathcal C$ to $\mathbf{Set}$ . It maps pairs of object to sets, and pairs of morphisms to functions. Since we are in a monoidal category, the morphisms are linear functions, but the mappings between sets are regular functions (see Appendix 1). Thus the action of the profunctor $p$ on morphisms is a function:

$(a' \multimap a) \to (b \multimap b') \to p a b \to p a' b'$

In Haskell:

class Profunctor p where
  dimap :: (a' %1-> a) -> (b %1-> b') -> p a b -> p a' b'

A Tambara module (a.k.a., a strong profunctor) is a profunctor equipped with the following mapping:

$\alpha_{a b c} \colon p a b \to p (c \otimes a) (c \otimes b)$

natural in $a$ and $b$ , dintural in $c$ .
In Haskell, this translates to a polymorphic function:

class (Profunctor p) => Tambara p where
   alpha :: forall a b c. p a b -> p (c, a) (c, b)

The linear lens $L a b s t$ is itself a Tambara module, for fixed $a b$ . To show this, let’s construct a mapping:

$\alpha_{s t c} \colon L a b s t \to L a b (c \otimes s) (c \otimes t)$

Expanding the definition:

$\int^{c''} (s \multimap c'' \otimes a)\times (c'' \otimes b \multimap t) \to$
$\; \int^{c' } (c \otimes s \multimap c' \otimes a)\times (c' \otimes b \multimap c \otimes t)$

By cocontinuity of the hom-set in $\mathbf{Set}$ , a mapping out of a coend is equivalent to an end:

$\int_{c''} \Big( (s \multimap c'' \otimes a)\times (c'' \otimes b \multimap t) \to$
$\;\int^{c' } (c \otimes s \multimap c' \otimes a)\times (c' \otimes b \multimap c \otimes t) \Big)$

Given a pair of linear arrows on the left we want to construct a coend on the right. We can do it by first lifting both arrow by $(c \otimes -)$ . We get:

$(c \otimes s \multimap c \otimes c'' \otimes a)\times (c \otimes c'' \otimes b \multimap c \otimes t)$

We can inject them into the coend on the right at $c' = c \otimes c''$ .

In Haskell, we construct the instance of the Profunctor class for the linear lens:

instance Profunctor (LinLensEx a b) where
  dimap f' g' (LinLensEx f g) = LinLensEx (f . f') (g' . g)

and the instance of Tambara:

instance Tambara (LinLensEx a b) where
  alpha (LinLensEx f g) = 
    LinLensEx (unassoc . second f) (second g . assoc)

Linear lenses can be composed and there is an identity linear lens:

$id_{a b} \colon L a b a b = \int^c (a \multimap c \otimes a)\times (c \otimes b \multimap b)$

given by injecting the pair $(id_a, id_b)$ at $c = I$ , the monoidal unit.

In Haskell, we can construct the identity lens using the left unitor (see Appendix 1):

idLens :: LinLensEx a b a b
idLens = LinLensEx unlunit lunit

The profunctor representation of a linear lens is given by an end over Tambara modules:

$L a b s t \cong \int_{p : Tamb} p a b \to p s t$

In Haskell, this translates to a type of functions polymorphic in Tambara modules:

type PLens a b s t = forall p. Tambara p => p a b -> p s t

The advantage of this representation is that it lets us compose linear lenses using simple function composition.

Here’s the categorical proof of the equivalence. Left to right: Given a triple: $(c, f \colon s \multimap c \otimes a, g \colon c \otimes b \multimap t)$ , we construct:

$p a b \xrightarrow{\alpha_{a b c}} p (c \otimes a) (c \otimes b) \xrightarrow{p f g} p s t$

Conversely, given a polymorphic (in Tambara modules) function $p a b \to p s t$ , we can apply it to the identity optic $id_{a b}$ and obtain $L a b s t$ .

In Haskell, this equivalence is witnessed by the following pair of functions:

fromPLens :: PLens a b s t -> LinLensEx a b s t
fromPLens f = f idLens

toPLens :: LinLensEx a b s t -> PLens a b s t
toPLens (LinLensEx f g) pab = dimap f g (alpha pab)

van Laarhoven representation

Similar to regular lenses, linear lenses have a functor-polymorphic van Laarhoven encoding. The difference is that we have to use endofunctors in the monoidal subcategory, where all arrows are linear:

class Functor f where
  fmap :: (a %1-> b) %1-> f a %1-> f b

Just like regular Haskell functors, linear functors are strong. We define strength as:

strength :: Functor f => (a, f b) %1-> f (a, b)
strength (a, fb) = fmap (eta a) fb

where eta is the unit of the currying adjunction (see Appendix 1).

With this definition, the van Laarhoven encoding of linear lenses is:

type VLL s t a b = forall f. Functor f => 
    (a %1-> f b) -> (s %1-> f t)

The equivalence of the two encodings is witnessed by a pair of functions:

toVLL :: LinLens s t a b -> VLL s t a b
toVLL lns f = fmap apply . strength . second f . lns

fromVLL :: forall s t a b. VLL s t a b -> LinLens s t a b
fromVLL vll s = unF (vll (F id) s)

Here, the functor F is defined as a linear pair (a tensor product):

data F a b x where
   F :: (b %1-> x) %1-> a %1-> F a b x
unF :: F a b x %1-> (b %1-> x, a)
unF (F bx a) = (bx, a)

with the obvious implementation of fmap

instance Functor (F a b) where
  fmap f (F bx a) = F (f . bx) a

You can find the categorical derivation of van Laarhoven representation in Appendix 2.

Linear optics

Linear lenses are but one example of more general linear optics. Linear optics are defined by the action of a monoidal category $\mathcal M$ on (possibly the same) monoidal category $\mathcal C$ :

$\bullet \colon \mathcal M \times \mathcal C \to \mathcal C$

In particular, one can define linear prisms and linear traversals using actions by a coproduct or a power series.

The existential form is given by:

$O a b s t = \int^{m \colon \mathcal M} (s \multimap m \bullet a)\times (m \bullet b \multimap t)$

There is a corresponding Tambara representation, with the following Tambara structure:

$\alpha_{a b m} \colon p a b \to p (m \bullet a) (m \bullet b)$

Incidentally, the two hom-sets in the definition of the optic can come from two different categories, so it’s possible to mix linear and non-linear arrows in one optic.

Appendix: 1 Closed monoidal category in Haskell

With the advent of linear types we now have two main categories lurking inside Haskell. They have the same objects–Haskell types– but the monoidal category has fewer arrows. These are the linear arrows $a \multimap b$ . They can be composed:

(.) :: (b %1-> c) %1-> (a %1-> b) %1-> a %1 -> c
(f . g) x = f (g x)

and there is an identity arrow for every object:

id :: a %1-> a
id a = a

In general, a tensor product in a monoidal category is a bifunctor: $\mathcal C \times \mathcal C \to \mathcal C$ . In Haskell, we identify the tensor product $\otimes$ with the built-in product (a, b). The difference is that, within the monoidal category, this product doesn’t have projections. There is no linear arrow $(a, b) \multimap a$ or $(a, b) \multimap b$ . Consequently, there is no diagonal map $a \multimap (a, a)$ , and the unit object $()$ is not terminal: there is no arrow $a \multimap ()$ .

We define the action of a bifunctor on a pair of linear arrows entirely within the monoidal category:

class Bifunctor p where
    bimap :: (a %1-> a') %1-> (b %1-> b') %1-> 
             p a b %1-> p a' b'
    first :: (a %1-> a') %1-> p a b %1-> p a' b
    first f = bimap f id
    second :: (b %1-> b') %1-> p a b %1-> p a b'
    second = bimap id

The product is itself an instance of this linear bifunctor:

instance Bifunctor (,) where
    bimap f g (a, b) = (f a, g b)

The tensor product has to satisfy coherence conditions–associativity and unit laws:

assoc :: ((a, b), c) %1-> (a, (b, c))
assoc ((a, b), c) = (a, (b, c))
unassoc :: (a, (b, c)) %1-> ((a, b), c)
unassoc (a, (b, c)) = ((a, b), c)

lunit :: ((), a) %1-> a
lunit ((), a) = a
unlunit :: a %1-> ((), a)
unlunit a = ((), a)

In Haskell, the type of arrows between any two objects is also an object. A category in which this is true is called closed. This identification is the consequence of the currying adjunction between the product and the function type. In a closed monoidal category, there is a corresponding adjunction between the tensor product and the object of linear arrows. The mapping out of a tensor product is equivalent to the mapping into the function object. In Haskell, this is witnessed by a pair of mappings:

curry :: ((a, b) %1-> c) %1-> (a %1-> (b %1-> c))
curry f x y = f (x, y)

uncurry :: (a %1-> (b %1-> c)) %1-> ((a, b) %1-> c)
uncurry f (x, y) = f x y

Every adjunction also defines a pair of unit and counit natural transformations:

eta :: a %1-> b %1-> (a, b)
eta a b = (a, b)

apply :: (a %1-> b, a) %-> b
apply (f, a) = f a

We can, for instance, use the unit to implement a point-free mapping of lenses:

toLinLens :: LinLensEx a b s t -> LinLens s t a b
toLinLens (LinLensEx f g) = first ((g .) . eta) . f

Finally, a note about the Haskell definition of a profunctor:

class Profunctor p where
  dimap :: (a' %1-> a) -> (b %1-> b') -> p a b -> p a' b'

Notice the mixing of two types of arrows. This is because a profunctor is defined as a mapping $\mathcal C^{op} \times \mathcal C \to \mathbf{Set}$ . Here, $\mathcal C$ is the monoidal category, so the arrows in it are linear. But p a b is just a set, and the mapping p a b -> p a' b' is just a regular function. Similarly, the type:

 (a' %1-> a)

is not treated as an object in $\mathcal C$ but rather as a set of linear arrows. In fact this hom-set is itself a profunctor:

newtype Hom a b = Hom (a %1-> b)

instance Profunctor Hom where
  dimap f g (Hom h) = Hom (g . h . f)

As you might have noticed, there are many definitions that extend the usual Haskel concepts to linear types. Since it makes no sense to re-introduce, and give new names to each of them, the linear extensions are written using multiplicity polymorphism. For instance, the most general currying function is written as:

curry :: ((a, b) %p -> c) %q -> a %p -> b %p -> c

covering four different combinations of multiplicities.

Appendix 2: van Laarhoven representation

We start by defining functorial strength in a monoidal category:

$\sigma_{a b} \colon a \otimes F b \multimap F (a \otimes b)$

To begin with, we can curry $\sigma$ . Thus we have to construct:

$a \multimap (F b \multimap F (a \otimes b))$

We have at our disposal the counit of the currying adjunction:

$\eta_{a b} \colon a \multimap (b \multimap a \otimes b)$

We can apply $\eta_{a b}$ to $a$ and lift the resulting map $(b \multimap a \otimes b)$ to arrive at $F b \multimap F (a \otimes b)$ .

Now let’s write the van Laarhoven representation as the end of the mapping of two linear hom-sets:

$\int_{F \colon [\mathcal C, \mathcal C]} (a \multimap F b) \to (s \multimap F t)$

We use the Yoneda lemma to replace $a \multimap F b$ with a set of natural transformations, written as an end over $x$ :

$\int_{F} \int_x \big( (b \multimap x) \multimap (a \multimap F x)\big) \to (s \multimap F t)$

We can uncurry it:

$\int_{F} \int_x \big( (b \multimap x) \otimes a \multimap F x \big) \to (s \multimap F t)$

and apply the ninja-Yoneda lemma in the functor category to get:

$s \multimap ((b \multimap t) \otimes a)$

Here, the ninja-Yoneda lemma operates on higher-order functors, such as $\Phi_{s t} F = (s \multimap F t)$ . It can be written as:

$\int_{F} \int_x (Gx \multimap Fx) \to \Phi_{s t} F \cong \Phi_{s t} G$

Appendix 3: My resource management curriculum

These are some of my blog posts and articles about resource management and its application to concurrent programming.

Strong Pointers and Resource Management in C++,
- Part 1, 1999
- Part 2, 2000
Walking Down Memory Lane, 2005 (with Andrei Alexandrescu)
unique ptr–How Unique is it?, 2009
Unique Objects, 2009
Race-free Multithreading, 2009
- Part 1: Ownership
- Part 2: Owner Polymorphism
Edward C++ hands, 2013

April 5, 2022

Teaching optics through conspiracy theories

Posted by Bartosz Milewski under Category Theory, Functional Programming, Haskell, Lens, Programming
[5] Comments

This post is based on the talk I gave at Functional Conf 2022. There is a video recording of this talk.

Disclaimers

Data types may contain secret information. Some of it can be extracted, some is hidden forever. We’re going to get to the bottom of this conspiracy.

No data types were harmed while extracting their secrets.

No coercion was used to make them talk.

We’re talking, of course, about unsafeCoerce, which should never be used.

Implementation hiding

The implementation of a function, even if it’s available for inspection by a programmer, is hidden from the program itself.

What is this function, with the suggestive name double, hiding inside?

`x`	`double x`
2	4
3	6
-1	-2

Best guess: It’s hiding 2. It’s probably implemented as:

double x = 2 * x

How would we go about extracting this hidden value? We can just call it with the unit of multiplication:

double 1
> 2

Is it possible that it’s implemented differently (assuming that we’ve already checked it for all values of the argument)? Of course! Maybe it’s adding one, multiplying by two, and then subtracting two. But whatever the actual implementation is, it must be equivalent to multiplication by two. We say that the implementaion is isomorphic to multiplying by two.

Functors

Functor is a data type that hides things of type a. Being a functor means that it’s possible to modify its contents using a function. That is, if we’re given a function a->b and a functorful of a‘s, we can create a functorful of b‘s. In Haskell we define the Functor class as a type constructor equipped with the method fmap:

class Functor f where
  fmap :: (a -> b) -> f a -> f b

A standard example of a functor is a list of a‘s. The implementation of fmap applies a function g to all its elements:

instance Functor [] where
  fmap g [] = []
  fmap g (a : as) = (g a) : fmap g as

Saying that something is a functor doesn’t guarantee that it actually “contains” values of type a. But most data structures that are functors will have some means of getting at their contents. When they do, you can verify that they change their contents after applying fmap. But there are some sneaky functors.

For instance Maybe a tells us: Maybe I have an a, maybe I don’t. But if I have it, fmap will change it to a b.

instance Functor Maybe where
  fmap g Empty = Empty
  fmap g (Just a) = Just (g a)

A function that produces values of type a is also a functor. A function e->a tells us: I’ll produce a value of type a if you ask nicely (that is call me with a value of type e). Given a producer of a‘s, you can change it to a producer of b‘s by post-composing it with a function g :: a -> b:

instance Functor ((->) e) where
  fmap g f = g . f

Then there is the trickiest of them all, the IO functor. IO a tells us: Trust me, I have an a, but there’s no way I could tell you what it is. (Unless, that is, you peek at the screen or open the file to which the output is redirected.)

Continuations

A continuation is telling us: Don’t call us, we’ll call you. Instead of providing the value of type a directly, it asks you to give it a handler, a function that consumes an a and returns the result of the type of your choice:

type Cont a = forall r. (a -> r) -> r

You’d suspect that a continuation either hides a value of type a or has the means to produce it on demand. You can actually extract this value by calling the continuation with an identity function:

runCont :: Cont a -> a
runCont k = k id

In fact Cont a is for all intents and purposes equivalent to a–it’s isomorphic to it. Indeed, given a value of type a you can produce a continuation as a closure:

mkCont :: a -> Cont a
mkCont a = \k -> k a

The two functions, runCont and mkCont are the inverse of each other thus establishing the isomorphism Cont a ~ a.

The Yoneda Lemma

Here’s a variation on the theme of continuations. Just like a continuation, this function takes a handler of a‘s, but instead of producing an x, it produces a whole functorful of x‘s:

type Yo f a = forall x. (a -> x) -> f x

Just like a continuation was secretly hiding a value of the type a, this data type is hiding a whole functorful of a‘s. We can easily retrieve this functorful by using the identity function as the handler:

runYo :: Functor f => Yo f a -> f a
runYo g = g id

Conversely, given a functorful of a‘s we can reconstruct Yo f a by defining a closure that fmap‘s the handler over it:

mkYo :: Functor f => f a -> Yo f a
mkYo fa = \g -> fmap g fa

Again, the two functions, runYo and mkYo are the inverse of each other thus establishing a very important isomorphism called the Yoneda lemma:

Yo f a ~ f a

Both continuations and the Yoneda lemma are defined as polymorphic functions. The forall x in their definition means that they use the same formula for all types (this is called parametric polymorphism). A function that works for any type cannot make any assumptions about the properties of that type. All it can do is to look at how this type is packaged: Is it passed inside a list, a function, or something else. In other words, it can use the information about the form in which the polymorphic argument is passed.

Existential Types

One cannot speak of existential types without mentioning Jean-Paul Sartre.
sartre_22
An existential data type says: There exists a type, but I’m not telling you what it is. Actually, the type has been known at the time of construction, but then all its traces have been erased. This is only possible if the data constructor is itself polymorphic. It accepts any type and then immediately forgets what it was.

Here’s an extreme example: an existential black hole. Whatever falls into it (through the constructor BH) can never escape.

data BlackHole = forall a. BH a

Even a photon can’t escape a black hole:

bh :: BlackHole
bh = BH "Photon"

We are familiar with data types whose constructors can be undone–for instance using pattern matching. In type theory we define types by providing introduction and elimination rules. These rules tell us how to construct and how to deconstruct types.

But existential types erase the type of the argument that was passed to the (polymorphic) constructor so they cannot be deconstructed. However, not all is lost. In physics, we have Hawking radiation escaping a black hole. In programming, even if we can’t peek at the existential type, we can extract some information about the structure surrounding it.

Here’s an example: We know we have a list, but of what?

data SomeList = forall a. SomeL [a]

It turns out that to undo a polymorphic constructor we can use a polymorphic function. We have at our disposal functions that act on lists of arbitrary type, for instance length:

length :: forall a. [a] -> Int

The use of a polymorphic function to “undo” a polymorphic constructor doesn’t expose the existential type:

len :: SomeList -> Int
len (SomeL as) = length as

Indeed, this works:

someL :: SomeList
someL = SomeL [1..10]
> len someL
> 10

Extracting the tail of a list is also a polymorphic function. We can use it on SomeList without exposing the type a:

trim :: SomeList -> SomeList
trim (SomeL []) = SomeL []
trim (SomeL (a: as)) = SomeL as

Here, the tail of the (non-empty) list is immediately stashed inside SomeList, thus hiding the type a.

But this will not compile, because it would expose a:

bad :: SomeList -> a
bad (SomeL as) = head as

Producer/Consumer

Existential types are often defined using producer/consumer pairs. The producer is able to produce values of the hidden type, and the consumer can consume them. The role of the client of the existential type is to activate the producer (e.g., by providing some input) and passing the result (without looking at it) directly to the consumer.

Here’s a simple example. The producer is just a value of the hidden type a, and the consumer is a function consuming this type:

data Hide b = forall a. Hide a (a -> b)

All the client can do is to match the consumer with the producer:

unHide :: Hide b -> b
unHide (Hide a f) = f a

This is how you can use this existential type. Here, Int is the visible type, and Char is hidden:

secret :: Hide Int
secret = Hide 'a' (ord)

The function ord is the consumer that turns the character into its ASCII code:

> unHide secret
> 97

Co-Yoneda Lemma

There is a duality between polymorphic types and existential types. It’s rooted in the duality between universal quantifiers (for all, $\forall$ ) and existential quantifiers (there exists, $\exists$ ).

The Yoneda lemma is a statement about polymorphic functions. Its dual, the co-Yoneda lemma, is a statement about existential types. Consider the following type that combines the producer of x‘s (a functorful of x‘s) with the consumer (a function that transforms x‘s to a‘s):

data CoYo f a = forall x. CoYo (f x) (x -> a)

What does this data type secretly encode? The only thing the client of CoYo can do is to apply the consumer to the producer. Since the producer has the form of a functor, the application proceeds through fmap:

unCoYo :: Functor f => CoYo f a -> f a
unCoYo (CoYo fx g) = fmap g fx

The result is a functorful of a‘s. Conversely, given a functorful of a‘s, we can form a CoYo by matching it with the identity function:

mkCoYo :: Functor f => f a -> CoYo f a
mkCoYo fa = CoYo fa id

This pair of unCoYo and mkCoYo, one the inverse of the other, witness the isomorphism

CoYo f a ~ f a

In other words, CoYo f a is secretly hiding a functorful of a‘s.

Contravariant Consumers

The informal terms producer and consumer, can be given more rigorous meaning. A producer is a data type that behaves like a functor. A functor is equipped with fmap, which lets you turn a producer of a‘s to a producer of b‘s using a function a->b.

Conversely, to turn a consumer of a‘s to a consumer of b‘s you need a function that goes in the opposite direction, b->a. This idea is encoded in the definition of a contravariant functor:

class Contravariant f where
  contramap :: (b -> a) -> f a -> f b

There is also a contravariant version of the co-Yoneda lemma, which reverses the roles of a producer and a consumer:

data CoYo' f a = forall x. CoYo' (f x) (a -> x)

Here, f is a contravariant functor, so f x is a consumer of x‘s. It is matched with the producer of x‘s, a function a->x.

As before, we can establish an isomorphism

CoYo' f a ~ f a

by defining a pair of functions:

unCoYo' :: Contravariant f => CoYo' f a -> f a
unCoYo' (CoYo' fx g) = contramap g fx

mkCoYo' :: Contravariant f => f a -> CoYo' f a
mkCoYo' fa = CoYo' fa id

Existential Lens

A lens abstracts a device for focusing on a part of a larger data structure. In functional programming we deal with immutable data, so in order to modify something, we have to decompose the larger structure into the focus (the part we’re modifying) and the residue (the rest). We can then recreate a modified data structure by combining the new focus with the old residue. The important observation is that we don’t care what the exact type of the residue is. This description translates directly into the following definition:

data Lens' s a =
  forall c. Lens' (s -> (c, a)) ((c, a) -> s)

Here, s is the type of the larger data structure, a is the type of the focus, and the existentially hidden c is the type of the residue. A lens is constructed from a pair of functions, the first decomposing s and the second recomposing it.
SimpleLens

Given a lens, we can construct two functions that don’t expose the type of the residue. The first is called get. It extracts the focus:

toGet :: Lens' s a -> (s -> a)
toGet (Lens' frm to) = snd . frm

The second, called set replaces the focus with the new value:

toSet :: Lens' s a -> (s -> a -> s)
toSet (Lens' frm to) = \s a -> to (fst (frm s), a)

Notice that access to residue not possible. The following will not compile:

bad :: Lens' s a -> (s -> c)
bad (Lens' frm to) = fst . frm

But how do we know that a pair of a getter and a setter is exactly what’s hidden in the existential definition of a lens? To show this we have to use the co-Yoneda lemma. First, we have to identify the producer and the consumer of c in our existential definition. To do that, notice that a function returning a pair (c, a) is equivalent to a pair of functions, one returning c and another returning a. We can thus rewrite the definition of a lens as a triple of functions:

data Lens' s a = 
  forall c. Lens' (s -> c) (s -> a) ((c, a) -> s)

The first function is the producer of c‘s, so the rest will define a consumer. Recall the contravariant version of the co-Yoneda lemma:

data CoYo' f s = forall c. CoYo' (f c) (s -> c)

We can define the contravariant functor that is the consumer of c‘s and use it in our definition of a lens. This functor is parameterized by two additional types s and a:

data F s a c = F (s -> a) ((c, a) -> s)

This lets us rewrite the lens using the co-Yoneda representation, with f replaced by (partially applied) F s a:

type Lens' s a = CoYo' (F s a) s

We can now use the isomorphism CoYo' f s ~ f s. Plugging in the definition of F, we get:

Lens' s a ~ CoYo' (F s a) s
CoYo' (F s a) s ~ F s a s
F s a s ~ (s -> a) ((s, a) -> s)

We recognize the two functions as the getter and the setter. Thus the existential representation of the lens is indeed isomorphic to the getter/setter pair.

Type-Changing Lens

The simple lens we’ve seen so far lets us replace the focus with a new value of the same type. But in general the new focus could be of a different type. In that case the type of the whole thing will change as well. A type-changing lens thus has the same decomposition function, but a different recomposition function:

data Lens s t a b =
forall c. Lens (s -> (c, a)) ((c, b) -> t)

As before, this lens is isomorphic to a get/set pair, where get extracts an a:

toGet :: Lens s t a b -> (s -> a)
toGet (Lens frm to) = snd . frm

and set replaces the focus with a new value of type b to produce a t:

toSet :: Lens s t a b -> (s -> b -> t)
toSet (Lens frm to) = \s b -> to (fst (frm s), b)

Other Optics

The advantage of the existential representation of lenses is that it easily generalizes to other optics. The idea is that a lens decomposes a data structure into a pair of types (c, a); and a pair is a product type, symbolically $c \times a$

data Lens s t a b =
forall c. Lens (s -> (c, a))
               ((c, b) -> t)

A prism does the same for the sum data type. A sum $c + a$ is written as Either c a in Haskell. We have:

data Prism s t a b =
forall c. Prism (s -> Either c a)
                (Either c b -> t)

We can also combine sum and product in what is called an affine type $c_1 + c_2 \times a$ . The resulting optic has two possible residues, c1 and c2:

data Affine s t a b =
forall c1 c2. Affine (s -> Either c1 (c2, a))
                     (Either c1 (c2, b) -> t)

The list of optics goes on and on.

Profunctors

A producer can be combined with a consumer in a single data structure called a profunctor. A profunctor is parameterized by two types; that is p a b is a consumer of a‘s and a producer of b‘s. We can turn a consumer of a‘s and a producer of b‘s to a consumer of s‘s and a producer of t‘s using a pair of functions, the first of which goes in the opposite direction:

class Profunctor p where
  dimap :: (s -> a) -> (b -> t) -> p a b -> p s t

The standard example of a profunctor is the function type p a b = a -> b. Indeed, we can define dimap for it by precomposing it with one function and postcomposing it with another:

instance Profunctor (->) where
  dimap in out pab = out . pab . in

Profunctor Optics

We’ve seen functions that were polymorphic in types. But polymorphism is not restricted to types. Here’s a definition of a function that is polymorphic in profunctors:

type Iso s t a b = forall p. Profunctor p =>
  p a b -> p s t

This function says: Give me any producer of b‘s that consumes a‘s and I’ll turn it into a producer of t‘s that consumes s‘s. Since it doesn’t know anything else about its argument, the only thing this function can do is to apply dimap to it. But dimap requires a pair of functions, so this profunctor-polymorphic function must be hiding such a pair:

s -> a
b -> t

Indeed, given such a pair, we can reconstruct it’s implementation:

mkIso :: (s -> a) -> (b -> t) -> Iso s t a b
mkIso g h = \p -> dimap g h p

All other optics have their corresponding implementation as profunctor-polymorphic functions. The main advantage of these representations is that they can be composed using simple function composition.

Main Takeaways

Producers and consumers correspond to covariant and contravariant functors
Existential types are dual to polymorphic types
Existential optics combine producers with consumers in one package
In such optics, producers decompose, and consumers recompose data
Functions can be polymorphic with respect to types, functors, or profunctors

December 28, 2021

Co-Presheaf Optics

Posted by Bartosz Milewski under Category Theory, Lens, Programming
Leave a Comment

A PDF version of this post is available on github.

Abstract

Co-presheaf optic is a new kind of optic that generalizes the polynomial lens. Its distinguishing feature is that it’s not based on the action of a monoidal category. Instead the action is parameterized by functors between different co-presheaves. The composition of these actions corresponds to composition of functors rather than the more traditional tensor product. These functors and their composition have a representation in terms of profunctors.

Motivation

A lot of optics can be defined using the existential, or coend, representation:

$\mathcal{O}\langle a, b\rangle \langle s, t \rangle = \int^{m \colon \mathcal M} \mathcal C (s, m \bullet a) \times \mathcal D ( m \bullet b, t)$

Here $\mathcal M$ is a monoidal category with an action on objects of two categories $\mathcal C$ and $\mathcal D$ (I’ll use the same notation for both actions). The actions are composed using the tensor product in $\mathcal M$ :

$n \bullet (m \bullet a) = (n \otimes m) \bullet a$

The idea of this optic is that we have a pair of morphisms, one decomposing the source $s$ into the action of some $m$ on $a$ , and the other recomposing the target $t$ from the action of the same $m$ on $b$ . In most applications we pick $\mathcal D$ to be the same category as $\mathcal C$ .

Recently, there has been renewed interest in polynomial functors. Morphisms between polynomial functors form a new kind of optic that doesn’t neatly fit this mold. They do, however, admit an existential representation or the form:

$\int^{c_{k i}} \prod_{k \in K} \mathbf{Set} \left(s_k, \sum_{n \in N} a_n \times c_{n k} \right) \times \prod_{i \in K} \mathbf{Set} \left(\sum_{m \in N} b_m \times c_{m i}, t_i \right)$

Here the sets $s_k$ and $t_i$ can be treated as fibers over the set $K$ , while the sets $a_n$ and $b_m$ are fibers over a different set $N$ .

Alternatively, we can treat these fibrations as functors from discrete categories to $\mathbf{Set}$ , that is co-presheaves. For instance $a_n$ is the result of a co-presheaf $a$ acting on an object $n$ of a discrete category $\mathcal N$ . The products over $K$ can be interpreted as ends that define natural transformations between co-presheaves. The interesting part is that the matrices $c_{n k}$ are fibrated over two different sets. I have previously interpreted them as profunctors:

$c \colon \mathcal N^{op} \times \mathcal K \to \mathbf{Set}$

In this post I will elaborate on this interpretation.

Co-presheaves

A co-presheaf category $[\mathcal C, Set ]$ behaves, in many respects, like a vector space. For instance, it has a “basis” consisting of representable functors $\mathcal C (r, -)$ ; in the sense that any co-presheaf is as a colimit of representables. Moreover, colimit-preserving functors between co-presheaf categories are very similar to linear transformations between vector spaces. Of particular interest are functors that are left adjoint to some other functors, since left adjoints preserve colimits.

The polynomial lens formula has a form suggestive of vector-space interpretation. We have one vector space with vectors $\vec{s}$ and $\vec{t}$ and another with $\vec{a}$ and $\vec{b}$ . Rectangular matrices $c_{n k}$ can be seen as components of a linear transformation between these two vector spaces. We can, for instance, write:

$\sum_{n \in N} a_n \times c_{n k} = c^T a$

where $c^T$ is the transposed matrix. Transposition here serves as an analog of adjunction.

We can now re-cast the polynomial lens formula in terms of co-presheaves. We no longer intepret $\mathcal N$ and $\mathcal K$ as discrete categories. We have:

$a, b \colon [\mathcal N, \mathbf{Set}]$

$s, t \colon [\mathcal K, \mathbf{Set}]$

In this interpretation $c$ is a functor between categories of co-presheaves:

$c \colon [\mathcal N, \mathbf{Set}] \to [\mathcal K, \mathbf{Set}]$

We’ll write the action of this functor on a presheaf $a$ as $c \bullet a$ .

We assume that this functor has a right adjoint and therefore preserves colimits.

$[\mathcal K, \mathbf{Set}] (c \bullet a, t) \cong [\mathcal N, \mathbf{Set}] (a, c^{\dagger} \bullet t)$

where:

$c^{\dagger} \colon [\mathcal K, \mathbf{Set}] \to [\mathcal N, \mathbf{Set}]$

We can now generalize the polynomial optic formula to:

$\mathcal{O}\langle a, b\rangle \langle s, t \rangle = \int^{c} [\mathcal K, \mathbf{Set}] \left(s, c \bullet a \right) \times [\mathcal K, \mathbf{Set}] \left(c \bullet b, t \right)$

The coend is taken over all functors that have a right adjoint. Fortunately there is a better representation for such functors. It turns out that colimit preserving functors:

$c \colon [\mathcal N, \mathbf{Set}] \to [\mathcal K, \mathbf{Set}]$

are equivalent to profunctors (see the Appendix for the proof). Such a profunctor:

$p \colon \mathcal N^{op} \times \mathcal K \to \mathbf{Set}$

is given by the formula:

$p \langle n, k \rangle = c ( \mathcal N(n, -)) k$

where $\mathcal N(n, -)$ is a representable co-presheaf.

The action of $c$ can be expressed as a coend:

$(c \bullet a) k = \int^{n} a(n) \times p \langle n, k \rangle$

The co-presheaf optic is then a coend over all profunctors $p \colon \mathcal N^{op} \times \mathcal K \to \mathbf{Set}$ :

$\int^{p} [\mathcal K, \mathbf{Set}] \left(s, \int^{n} a(n) \times p \langle n, - \rangle \right) \times [\mathcal K, \mathbf{Set}] \left(\int^{n'} b(n') \times p \langle n', - \rangle, t \right)$

Composition

We have defined the action $c \bullet a$ as the action of a functor on a co-presheaf. Given two composable functors:

$c \colon [\mathcal N, \mathbf{Set}] \to [\mathcal K, \mathbf{Set}]$

and:

$c' \colon [\mathcal K, \mathbf{Set}] \to [\mathcal M, \mathbf{Set}]$

we automatically get the associativity law:

$c' \bullet (c \bullet a) = (c' \circ c) a$

The composition of functors between co-presheaves translates directly to profunctor composition. Indeed, the profunctor $p' \diamond p$ corresponding to $c' \circ c$ is given by:

$(p' \diamond p) \langle n, m \rangle = (c' \circ c) ( \mathcal N(n, -)) m$

and can be evaluated to:

$(c' ( c ( \mathcal N(n, -))) m \cong \int^{k} c ( \mathcal N(n, -)) k \times p' \langle k, m \rangle$

$\cong \int^{k} p \langle n, k \rangle \times p' \langle k, m \rangle$

which is the standard definition of profunctor composition.

Consider two composable co-presheaf optics, $\mathcal{O}\langle a, b\rangle \langle s, t \rangle$ and $\mathcal{O}\langle a', b' \rangle \langle a, b \rangle$ . The first one tells us that there exists a $c$ and a pair of natural transformations:

$l_c (s, a ) = [\mathcal K, \mathbf{Set}] \left(s, c \bullet a \right)$

$r_c (b, t) = [\mathcal K, \mathbf{Set}] \left(c \bullet b, t \right)$

The second tells us that there exists a $c'$ and a pair:

$l'_{c'} (a, a' ) = [\mathcal K, \mathbf{Set}] \left(a, c' \bullet a' \right)$

$r'_{c'} (b', b) = [\mathcal K, \mathbf{Set}] \left(c' \bullet b', b \right)$

The composition of the two should be an optic of the type $\mathcal{O}\langle a', b'\rangle \langle s, t \rangle$ . Indeed, we can construct such an optic using the composition $c' \circ c$ and a pair of natural transformations:

$s \xrightarrow{l_c (s, a )} c \bullet a \xrightarrow{c \,\circ \, l'_{c'} (a, a')} c \bullet (c' \bullet a') \xrightarrow{assoc} (c \circ c') \bullet a'$

$(c \circ c') \bullet b' \xrightarrow{assoc^{-1}} c \bullet (c' \bullet b') \xrightarrow{c \, \circ \, r'_{c'} (b', b)} c \bullet b \xrightarrow{r_c (b, t)} t$

Generalizations

By duality, there is a corresponding optic based on presheaves. Also, (co-) presheaves can be naturally generalized to enriched categories, where the correspondence between left adjoint functors and enriched profunctors holds as well.

Appendix

I will show that a functor between two co-presheaves that has a right adjoint and therefore preserves colimits:

$c \colon [\mathcal N, \mathbf{Set}] \to [\mathcal K, \mathbf{Set}]$

is equivalent to a profunctor:

$p \colon \mathcal N^{op} \times \mathcal K \to \mathbf{Set}$

The profunctor is given by:

$p \langle n, k \rangle = c ( \mathcal N(n, -)) k$

and the functor $c$ can be recovered using the formula:

$c (a) k = \int^{n'} a (n') \times p \langle n', k \rangle$

where:

$a \colon [\mathcal N, \mathbf{Set}]$

I’ll show that these formulas are the inverse of each other. First, inserting the formula for $c$ into the definition of $p$ should gives us $p$ back:

$\int^{n'} \mathcal N(n, -) (n') \times p\langle n', k \rangle \cong p \langle n, k \rangle$

which follows from the co-Yoneda lemma.

Second, inserting the formula for $p$ into the definition of $c$ should give us $c$ back:

$\int^{n'} a n' \times c(\mathcal N(n', -)) k \cong c (a) k$

Since $c$ preserves all colimits, and any co-presheaf is a colimit of representables, it’s enough that we prove this identity for a representable:

$a (n) = \mathcal N (r, n)$

We have to show that:

$\int^{n'} \mathcal N (r, n') \times c(\mathcal N(n', -)) k \cong c ( \mathcal N (r, -) ) k$

and this follows from the co-Yoneda lemma.

December 10, 2021

Profunctor Representation of a Polynomial Lens

Posted by Bartosz Milewski under Category Theory, Lens, Programming
Leave a Comment

A PDF of this post is available on github.

Motivation

In this post I’ll be looking at a subcategory of $\mathbf{Poly}$ that consists of polynomial functors in which the fibration is done over one fixed set $N$ :

$P(y) = \sum_{n \in N} s_n \times \mathbf{Set}(t_n, y)$

The reason for this restriction is that morphisms between such functors, which are called polynomial lenses, can be understood in terms of monoidal actions. Optics that have this property automatically have profunctor representation. Profunctor representation has the advantage that it lets us compose optics using regular function composition.

Previously I’ve explored the representations of polynomial lenses as optics in terms on functors and profunctors on discrete categories. With just a few modifications, we can make these categories non-discrete. The trick is to replace sums with coends and products with ends; and, when appropriate, interpret ends as natural transformations.

Monoidal Action

Here’s the existential representation of a lens between polynomials in which all fibrations are over the same set $N$ :

$\mathbf{Pl}\langle s, t\rangle \langle a, b\rangle \cong$

$\int^{c_{k i}} \prod_{k \in N} \mathbf{Set} \left(s_k, \sum_{n \in N} a_n \times c_{n k} \right) \times \prod_{i \in N} \mathbf{Set} \left(\sum_{m \in N} b_m \times c_{m i}, t_i \right)$

This makes the matrices $c_{n k}$ “square.” Such matrices can be multiplied using a version of matrix multiplication.

Interestingly, this idea generalizes naturally to a setting in which $N$ is replaced by a non-discrete category $\mathcal{N}$ . In this setting, we’ll write the residues $c_{m n}$ as profunctors:

$c \langle m, n \rangle \colon \mathcal{N}^{op} \times \mathcal{N} \to \mathbf{Set}$

They are objects in the monoidal category in which the tensor product is given by profunctor composition:

$(c \diamond c') \langle m, n \rangle = \int^{k \colon \mathcal{N}} c \langle m, k \rangle \times c' \langle k, n \rangle$

and the unit is the hom-functor $\mathcal{N}(m, n)$ . (Incidentally, a monoid in this category is called a promonad.)

In the case of $\mathcal{N}$ a discrete category, these definitions decay to standard matrix multiplication:

$\sum_k c_{m k} \times c'_{k n}$

and the Kronecker delta $\delta_{m n}$ .

We define the monoidal action of the profunctor $c$ acting on a co-presheaf $a$ as:

$(c \bullet a) (m) = \int^{n \colon \mathcal{N}} a(n) \times c \langle n, m \rangle$

This is reminiscent of a vector being multiplied by a matrix. Such an action of a monoidal category equips the co-presheaf category with the structure of an actegory.

A product of hom-sets in the definition of the existential optic turns into a set of natural transformations in the functor category $[\mathcal{N}, \mathbf{Set}]$ .

$\mathbf{Pl}\langle s, t\rangle \langle a, b\rangle \cong \int^{c \colon [\mathcal{N}^{op} \times \mathcal{N}, Set]} [\mathcal{N}, \mathbf{Set}] \left(s, c \bullet a\right) \times [\mathcal{N}, \mathbf{Set}] \left(c \bullet b, t\right)$

Or, using the end notation for natural transformations:

$\int^{c} \left( \int_m \mathbf{Set}\left(s(m), (c \bullet a)(m)\right) \times \int_n \mathbf{Set} \left((c \bullet b)(n), t(n)\right) \right)$

As before, we can eliminate the coend if we can isolate $c$ in the second hom-set using a series of isomorphisms:

$\int_n \mathbf{Set} \left(\int^k b(k) \times c\langle k, n \rangle , t(n) \right)$

$\cong \int_n \int_k \mathbf{Set}\left( b(k) \times c\langle k, n \rangle , t (n)\right)$

$\cong \int_{n, k} \mathbf{Set}\left(c\langle k, n \rangle , [b(k), t (n)]\right)$

I used the fact that a mapping out of a coend is an end. The result, after applying the Yoneda lemma to eliminate the end over $k$ , is:

$\mathbf{Pl}\langle s, t\rangle \langle a, b\rangle \cong \int_m \mathbf{Set}\left(s(m), \int^j a(j) \times [b(j), t(m)] \right)$

or, with some abuse of notation:

$[\mathcal{N}, \mathbf{Set}] ( s, [b, t] \bullet a)$

When $\mathcal{N}$ is discrete, this formula decays to the one for polynomial lens.

Profunctor Representation

Since this poly-lens is a special case of a general optic, it automatically has a profunctor representation. The trick is to define a generalized Tambara module, that is a category $\mathcal{T}$ of profunctors of the type:

$P \colon [\mathcal{N}, \mathbf{Set}]^{op} \times [\mathcal{N}, \mathbf{Set}] \to \mathbf{Set}$

with additional structure given by the following family of transformations, in components:

$\alpha_{c, s, t} \colon P\langle s, t \rangle \to P \left \langle c \bullet s, c \bullet t \right \rangle$

The profunctor representation of the polynomial lens is then given by an end over all profunctors in this Tambara category:

$\mathbf{Pl}\langle s, t\rangle \langle a, b\rangle \cong \int_{P \colon \mathcal{T}} \mathbf{Set}\left ( (U P)\langle a, b \rangle, (U P) \langle s, t \rangle \right)$

Where $U$ is the obvious forgetful functor from $\mathcal{T}$ to the underlying profunctor category$.

December 9, 2021

Polynomial Lens in Idris

Posted by Bartosz Milewski under Category Theory, Idris, Lens, Programming
[2] Comments

Lenses and, more general, optics are an example of hard-core category theory that has immediate application in programming. While working on polynomial lenses, I had a vague idea how they could be implemented in a programming language. I thought up an example of a polynomial lens that would focus on all the leaves of a tree at once. It could retrieve or modify them in a single operation. There already is a Haskell optic called traversal that could do it. It can safely retrieve a list of leaves from a tree. But there is a slight problem when it comes to replacing them: the size of the input list has to match the number of leaves in the tree. If it doesn’t, the traversal doesn’t work.

A polynomial lens adds an additional layer of safety by keeping track of the sizes of both the trees and the lists. The problem is that its implementation requires dependent types. Haskell has some support for dependent types, so I tried to work with it, but I quickly got bogged down. So I decided to bite the bullet and quickly learn Idris. This was actually easier than I expected and this post is the result.

Counted Vectors and Trees

I started with the “Hello World!” of dependent types: counted vectors. Notice that, in Idris, type signatures use a single colon rather than the Haskell’s double colon. You can quickly get used to it after the compiler slaps you a few times.

data Vect : Type -> Nat -> Type where
  VNil : Vect a Z
  VCons : (x: a) -> (xs : Vect a n) -> Vect a (S n)

If you know Haskell GADTs, you can easily read this definition. In Haskell, we usually think of Nat as a “kind”, but in Idris types and values live in the same space. Nat is just an implementation of Peano artithmetics, with Z standing for zero, and (S n) for the successor of n. Here, VNil is the constructor of an empty vector of size Z, and VCons prepends a value of type a to the tail of size n resulting in a new vector of size (S n). Notice that Idris is much more explicit about types than Haskell.

The power of dependent types is in very strict type checking of both the implementation and of usage of functions. For instance, when mapping a function over a vector, we can make sure that the result is the same size as the argument:

mapV : (a -> b) -> Vect a n -> Vect b n
mapV f VNil = VNil
mapV f (VCons a v) = VCons (f a) (mapV f v)

When concatenating two vectors, the length of the result must be the sum of the two lengths, (plus m n):

concatV : Vect a m -> Vect a n -> Vect a (plus m n)
concatV VNil v = v
concatV (VCons a w) v = VCons a (concatV w v)

Similarly, when splitting a vector in two, the lengths must match, too:

splitV : (n : Nat) -> Vect a (plus n m) -> (Vect a n, Vect a m)
splitV Z v = (VNil, v)
splitV (S k) (VCons a v') = let (v1, v2) = splitV k v'
                            in (VCons a v1, v2)

Here’s a more complex piece of code that implements insertion sort:

sortV : Ord a => Vect a n -> Vect a n
sortV VNil = VNil
sortV (VCons x xs) = let xsrt = sortV xs 
                     in (ins x xsrt)
  where
    ins : Ord a => (x : a) -> (xsrt : Vect a n) -> Vect a (S n)
    ins x VNil = VCons x VNil
    ins x (VCons y xs) = if x < y then VCons x (VCons y xs)
                                  else VCons y (ins x xs)

In preparation for the polynomial lens example, let’s implement a node-counted binary tree. Notice that we are counting nodes, not leaves. That’s why the node count for Node is the sum of the node counts of the children plus one:

data Tree : Type -> Nat -> Type where
  Empty : Tree a Z
  Leaf  : a -> Tree a (S Z)
  Node  : Tree a n -> Tree a m -> Tree a (S (plus m  n))

All this is not much different from what you’d see in a Haskell library.

Existential Types

So far we’ve been dealing with function that return vectors whose lengths can be easily calculated from the inputs and verified at compile time. This is not always possible, though. In particular, we are interested in retrieving a vector of leaves from a tree that’s parameterized by the number of nodes. We don’t know up front how many leaves a given tree might have. Enter existential types.

An existential type hides part of its implementation. An existential vector, for instance, hides its size. The receiver of an existential vector knows that the size “exists”, but its value is inaccessible. You might wonder then: What can be done with such a mystery vector? The only way for the client to deal with it is to provide a function that is insensitive to the size of the hidden vector. A function that is polymorphic in the size of its argument. Our sortV is an example of such a function.

Here’s the definition of an existential vector:

data SomeVect : Type -> Type where
  HideV : {n : Nat} -> Vect a n -> SomeVect a

SomeVect is a type constructor that depends on the type a—the payload of the vector. The data constructor HideV takes two arguments, but the first one is surrounded by a pair of braces. This is called an implicit argument. The compiler will figure out its value from the type of the second argument, which is Vect a n. Here’s how you construct an existential:

secretV : SomeVect Int
secretV = HideV (VCons 42 VNil)

In this case, the compiler will deduce n to be equal to one, but the recipient of secretV will have no way of figuring this out.

Since we’ll be using types parameterized by Nat a lot, let’s define a type synonym:

Nt : Type
Nt = Nat -> Type

Both Vect a and Tree a are examples of this type.

We can also define a generic existential for stashing such types:

data Some : Nt -> Type where
  Hide : {n : Nat} -> nt n -> Some nt

and some handy type synonyms:

SomeVect : Type -> Type
SomeVect a = Some (Vect a)

SomeTree : Type -> Type
SomeTree a = Some (Tree a)

Polynomial Lens

We want to translate the following categorical definition of a polynomial lens:

$\mathbf{PolyLens}\langle s, t\rangle \langle a, b\rangle = \prod_{k} \mathbf{Set}\left(s_k, \sum_{n} a_n \times [b_n, t_k] \right)$

We’ll do it step by step. First of all, we’ll assume, for simplicity, that the indices $k$ and $n$ are natural numbers. Therefore the four arguments to PolyLens are types parameterized by Nat, for which we have a type alias:

PolyLens : Nt -> Nt -> Nt -> Nt -> Type

The definition starts with a big product over all $k$ ‘s. Such a product corresponds, in programming, to a polymorphic function. In Haskell we would write it as forall k. In Idris, we’ll accomplish the same using an implicit argument {k : Nat}.

The hom-set notation $\mathbf{Set}(a, b)$ stands for a set of functions from $a$ to $b$ , or the type a -> b. So does the notation $[a, b]$ (the internal hom is the same as the external hom in $\mathbf{Set}$ ). The product $a \times b$ is the type of pairs (a, b).

The only tricky part is the sum over $n$ . A sum corresponds exactly to an existential type. Our SomeVect, for instance, can be considered a sum over n of all vector types Vect a n.

Here’s the intuition: Consider that to construct a sum type like Either a b it’s enough to provide a value of either type a or type b. Once the Either is constructed, the information about which one was used is lost. If you want to use an Either, you have to provide two functions, one for each of the two branches of the case statement. Similarly, to construct SomeVect its enough to provide a vector of some particular lenght n. Instead of having two possibilities of Either, we have infinitely many possibilities corresponding to different n‘s. The information about what n was used is then promptly lost.

The sum in the definition of the polynomial lens:

$\sum_{n} a_n \times [b_n, t_k]$

can be encoded in this existential type:

data SomePair : Nt -> Nt -> Nt -> Type where
  HidePair : {n : Nat} -> 
             (k : Nat) -> a n -> (b n -> t k) -> SomePair a b t

Notice that we are hiding n, but not k.

Taking it all together, we end up with the following type definition:

PolyLens : Nt -> Nt -> Nt -> Nt -> Type
PolyLens s t a b = {k : Nat} -> s k -> SomePair a b t

The way we read this definition is that PolyLens is a function polymorphic in k. Given a value of the type s k it produces and existential pair SomePair a b t. This pair contains a value of the type a n and a function b n -> t k. The important part is that the value of n is hidden from the caller inside the existential type.

Using the Lens

Because of the existential type, it’s not immediately obvious how one can use the polynomial lens. For instance, we would like to be able to extract the foci a n, but we don’t know what the value of n is. The trick is to hide n inside an existential Some. Here is the “getter” for this lens:

getLens :  PolyLens sn tn an bn -> sn n -> Some an
getLens lens t =
  let  HidePair k v _ = lens t
  in Hide v

We call lens with the argument t, pattern match on the constructor HidePair and immediately hide the contents back using the constructor Hide. The compiler is smart enough to know that the existential value of n hasn’t been leaked.

The second component of SomePair, the “setter”, is trickier to use because, without knowing the value of n, we don’t know what argument to pass to it. The trick is to take advantage of the match between the producer and the consumer that are the two components of the existential pair. Without disclosing the value of n we can take the a‘s and use a polymorphic function to transform them into b‘s.

transLens : PolyLens sn tn an bn -> ({n : Nat} -> an n -> bn n)
        -> sn n -> Some tn
transLens lens f t =
  let  HidePair k v vt = lens t
  in  Hide (vt (f v))

The polymorphic function here is encoded as ({n : Nat} -> an n -> bn n). (An example of such a function is sortV.) Again, the value of n that’s hidden inside SomePair is never leaked.

Example

Let’s get back to our example: a polynomial lens that focuses on the leaves of a tree. The type signature of such a lens is:

treeLens : PolyLens (Tree a) (Tree b) (Vect a) (Vect b)

Using this lens we should be able to retrieve a vector of leaves Vect a n from a node-counted tree Tree a k and replace it with a new vector Vect b n to get a tree Tree b k. We should be able to do it without ever disclosing the number of leaves n.

To implement this lens, we have to write a function that takes a tree of a and produces a pair consisting of a vector of a‘s and a function that takes a vector of b‘s and produces a tree of b‘s. The type b is fixed in the signature of the lens. In fact we can pass this type to the function we are implementing. This is how it’s done:

treeLens : PolyLens (Tree a) (Tree b) (Vect a) (Vect b)
treeLens {b} t = replace b t

First, we bring b into the scope of the implementation as an implicit parameter {b}. Then we pass it as a regular type argument to replace. This is the signature of replace:

replace : (b : Type) -> Tree a n -> SomePair (Vect a) (Vect b) (Tree b)

We’ll implement it by pattern-matching on the tree.

The first case is easy:

replace b Empty = HidePair 0 VNil (\v => Empty)

For an empty tree, we return an empty vector and a function that takes and empty vector and recreates and empty tree.

The leaf case is also pretty straightforward, because we know that a leaf contains just one value:

replace b (Leaf x) = HidePair 1 (VCons x VNil) 
                                (\(VCons y VNil) => Leaf y)

The node case is more tricky, because we have to recurse into the subtrees and then combine the results.

replace b (Node t1 t2) =
  let (HidePair k1 v1 f1) = replace b t1
      (HidePair k2 v2 f2) = replace b t2
      v3 = concatV v1 v2
      f3 = compose f1 f2
  in HidePair (S (plus k2 k1)) v3 f3

Combining the two vectors is easy: we just concatenate them. Combining the two functions requires some thinking. First, let’s write the type signature of compose:

compose : (Vect b n -> Tree b k) -> (Vect b m -> Tree b j) ->
       (Vect b (plus n m)) -> Tree b (S (plus j k))

The input is a pair of functions that turn vectors into trees. The result is a function that takes a larger vector whose size is the sume of the two sizes, and produces a tree that combines the two subtrees. Since it adds a new node, its node count is the sum of the node counts plus one.

Once we know the signature, the implementation is straightforward: we have to split the larger vector and pass the two subvectors to the two functions:

compose {n} f1 f2 v =
  let (v1, v2) = splitV n v
  in Node (f1 v1) (f2 v2)

The split is done by looking at the type of the first argument (Vect b n -> Tree b k). We know that we have to split at n, so we bring {n} into the scope of the implementation as an implicit parameter.

Besides the type-changing lens (that changes a to b), we can also implement a simple lens:

treeSimpleLens : PolyLens (Tree a) (Tree a) (Vect a) (Vect a)
treeSimpleLens {a} t = replace a t

We’ll need it later for testing.

Testing

To give it a try, let’s create a small tree with five nodes and three leaves:

t3 : Tree Char 5
t3 = (Node (Leaf 'z') (Node (Leaf 'a') (Leaf 'b')))

We can extract the leaves using our lens:

getLeaves : Tree a n -> SomeVect a
getLeaves t = getLens treeSimpleLens t

As expected, we get a vector containing 'z', 'a', and 'b'.

We can also transform the leaves using our lens and the polymorphic sort function:

trLeaves : ({n : Nat} -> Vect a n -> Vect b n) -> Tree a n -> SomeTree b
trLeaves f t = transLens treeLens f t

trLeaves sortV

The result is a new tree: ('a',('b','z'))

Complete code is available on github.

September 4, 2021

Dependent Optics

Posted by Bartosz Milewski under Category Theory, Functional Programming, Lens, Programming
Leave a Comment

A PDF version of this post is available on GitHub.

Dependent types, in programming, are families of types indexed by elements of an indexing type. For instance, counted vectors are families of tuples indexed by natural numbers—the lengths of the vectors.

In category theory we model dependent types as fibrations. We start with the total space $E$ , the base space $B$ , and a projection, or a display map, $p \colon E \to B$ . The fibers of $p$ correspond to members of the type family. For instance, the total space, or the bundle, of counted vectors is the list type $\mathit{List} (A)$ (a free monoid generated by $A$ ) with the projection $\mathit{len} \colon \mathit{List} (A) \to \mathbb{N}$ that returns the length of a list.

Another way of looking at dependent types is as objects in the slice category $\mathcal{C}/B$ . Counted vectors, for instance, are represented as objects in $\mathcal{C}/\mathbb{N}$ given by pairs $\langle \mathit{List} (A), \mathit{len} \rangle$ . Morphisms in the slice category correspond to fibre-wise mappings between bundles.

We often require that $\mathcal{C}$ be a locally cartesian closed category, that is a category whose slice categories are cartesian closed. In such categories, the base-change functor $f^*$ has both the left adjoint, the dependent sum $\Sigma_f$ ; and the right adjoint, the dependent product $\Pi_f$ . The base-change functor is defined as a pullback:

basechange

This pullback defines a cartesian product in the slice category $\mathcal{C}/B$ between two objects: $\langle B', f \rangle$ and $\langle E, p \rangle$ . In a locally cartesian closed category, this product has the right adjoint, the internal hom in $\mathcal{C}/B$ .

Dependent optics

The most general optic is given by two monoidal actions $L_m$ and $R_m$ in two categories $\mathcal{C}$ and $\mathcal{D}$ . It can be written as the following coend of the product of two hom-sets:

$O(A, A'; S, S') = \int^{m \colon \mathcal{M}} \mathcal{C}( S, L_m A) \times \mathcal{D}(R_m A', S')$

Monoidal actions are parameterized by objects in a monoidal category $(\mathcal{M}, \otimes, 1)$ .

Dependent optics are a special case of general optics, where one or both categories in question are slice categories. When the monoidal action is defined in the slice category, the transformations must respect fibrations. For instance, the action in the bundle $\langle E, p \rangle$ over $B$ must commute with the projection:

$p \circ L_m = p$

This is reminiscent of gauge transformations in physics, which act on fibers in bundles over spacetime. The action must respect the monoidal structure of $\mathcal{M}$ so, for instance,

$L_{m \otimes n} \cong L_m \circ L_n$

$L_1 \cong \mathit{Id}$

We can define a dependent (mixed) optic as:

$\int^{m : \mathcal{M}} (\mathcal{C}/B)( S, L_m A) \times (\mathcal{D}/B')(R_m A', S')$

Just like regular optics, dependent optics can be represented using Tambara modules, which are profunctors with the additional structure given by transformations:

$\alpha_{m, \langle A, A' \rangle} \colon P \langle A, A' \rangle \to P\langle L_m A, R_m A' \rangle$

where $A$ and $A'$ are objects in the appropriate slice categories.
The optic is then given by the following end in the Tambara category:

$O(A, A'; S, S') = \int_{p : \mathbf{Tam}} \mathbf{Set}(P \langle A, A' \rangle, P \langle S, S' \rangle)$

Dependent lens

The primordial optic, the lens, is defined by the monoidal action of a product. By analogy, we define a dependent lens by the action of the product in a slice category. The action parameterized by an object $\langle C, q \rangle$ on another object $\langle A, p \rangle$ is given by the pullback:

$M_C A = C \times_B A$

Since a pullback is the product in the slice category $\mathcal{C}/B$ , it is automatically associative and unital, so it can be used to define a dependent lens:

$\mathit{DLens}(A, A'; S, S') = \int^{\langle C, p \rangle : \mathcal{C}/B} (\mathcal{C}/B)( S, C \times_B A) \times (\mathcal{C}/B)(C \times_B A', S')$

Since $\mathcal{C}$ is locally cartesian closed, there is an adjunction between the product and the exponential. We can use it to get:

$\cong \int^{\langle C, p \rangle : \mathcal{C}/B} (\mathcal{C}/B)( S, C \times_B A) \times (\mathcal{C}/B)(C , [A', S']_B)$

We can then apply the Yoneda lemma to get the setter/getter form:

$(\mathcal{C}/B)( S, [A', S']_B \times_B A)$

The internal hom $[A', S']_B$ in a locally cartesian closed category can be expressed using a dependent product:

$\left [\left \langle A' \atop p \right \rangle, \left \langle S' \atop q \right \rangle \right ] \cong \Pi_p \left(p^* \left \langle S' \atop q \right \rangle \right)$

where $p \colon A' \to B$ is the fibration of $A'$ , $\Pi_p$ is the right adjoint to the base change functor, and $p^*$ is the base-change functor along $p$ .

The dependent lens can be written as:

$(\mathcal{C} / B) \left( \left \langle S \atop r \right \rangle, \Pi_p \left(p^* \left \langle S' \atop q \right \rangle \right) \times \left \langle A \atop r' \right \rangle \right)$

In particular, if $B$ is $\mathbb{N}$ , this is equal to an infinite tuple of functions:

$O(A, B; S, T) \cong \prod_n \left( s_n \to \left((b_n \to t_n) \times a_n \right) \right)$

or fiber-wise pairs of setter/getter $\langle s_n \to b_n \to t_n, s_n \to a_n \rangle$ indexed by $n$ .

Traversals

Traversals are optics whose monoidal action is generated by polynomial functors of the form:

$M_{c} a = \sum_{n \colon \mathbb{N}} c_n \times a^n$

The coefficients $c_n$ can be expressed as a fibration $\langle C, p \colon C \to \mathbb{N} \rangle$ , with $C = \sum_n c_n$ , the sum of the fibers. The set of powers of $a$ can be similarly written as $\langle L(a), \mathit{len} \rangle$ , with $L(a)$ the type of list of $a$ (a free monoid generated by $a$ ), and $\mathit{len}$ the function that assigns the length to a list. The monoidal action can then be written using a product (pullback) in the slice category $\mathbf{Set}/\mathbb{N}$ :

$\left \langle {C \atop p} \right \rangle \times \left \langle {L(a) \atop \mathit{len}} \right \rangle$

There is an obvious forgetful functor $U \colon \mathbf{Set}/\mathbb{N} \to \mathbf{Set}$ , which can be used to express the polynomial action:

$M_c a = U\left( \left \langle {C \atop p} \right \rangle \times \left \langle {L(a) \atop \mathit{len}} \right \rangle \right)$

The traversal is the optic:

$\int^{\langle C, p \rangle : \mathbf{Set}/\mathbb{N}} \mathbf{Set} \left(s, M_c a \right) \times \mathbf{Set}(M_c b, t)$

Eqivalently, the second factor can be rewritten as:

$\mathbf{Set}\left( \sum_{n \colon \mathbb{N}} c_n \times b^n, t\right) \cong \prod_{n \colon \mathbb{N}} \mathbf{Set}(c_n \times b^n, t)$

This, in turn, is equivalent to a single hom-set in the slice category:

$\cong (\mathbf{Set}/\mathbb{N})\left(\left \langle {C \atop p} \right \rangle \times \left \langle {L(b) \atop \mathit{len}} \right \rangle, \left \langle {\mathbb{N} \times t \atop \pi_1} \right \rangle \right)$

where $\pi_1$ is the projection from the cartesian product.

The traversal is therefore a mixed optic:

$\int^{\langle C, p \rangle : \mathbf{Set}/\mathbb{N}} \mathbf{Set} \left(s, M_c a \right) \times (\mathbf{Set}/\mathbb{N})\left( \left \langle {C \atop p} \right \rangle \times \left \langle {L(b) \atop \mathit{len}} \right \rangle, \left \langle {\mathbb{N} \times t \atop \pi_1} \right \rangle \right)$

The second factor can be transformed using the internal hom adjunction:

$(\mathbf{Set}/\mathbb{N})\left(\left \langle {C \atop p} \right \rangle, \left[ \left \langle {L(b) \atop \mathit{len}} \right \rangle, \left \langle {\mathbb{N} \times t \atop \pi_1} \right \rangle \right] \right)$

We can then use the ninja Yoneda lemma on the optic to “integrate” over $\langle C, p \rangle$ and get:

$O(a, b; s, t) \cong \mathbf{Set} \left( s, U\left( \left[ \left \langle {L(b) \atop \mathit{len}} \right \rangle, \left \langle {\mathbb{N} \times t \atop \pi_1} \right \rangle \right] \times \left \langle {L(a) \atop \mathit{len}} \right \rangle \right) \right)$

which, in components, reads:

$s \to \sum_n \left( (b^n \to t) \times a^n \right)$

April 1, 2021

Traversals 3: Existential and Profunctor representations of Traversals

Posted by Bartosz Milewski under Programming | Tags: Category Theory, Lens, Polynomial Functors, Profunctors, Tambara Modules, Traversal |
Leave a Comment

Previously: Profunctors.

Traversals

A traversal is a kind of optic that can focus on zero or more items at a time. Naively, we would expect to have a getter that returns a list of values, and a setter that replaces a list of values. Think of a tree with $N$ leaves: a traversal would return a list of leaves, and it would allow you to replace them with a new list. The problem is that the size of the list you pass to the setter cannot be arbitrary—it must match the number of leaves in the particular tree. This is why, in Haskell, the setter and the getter are usually combined in a single function:

s -> ([b] -> t, [a])

Still, Haskell is not able to force the sizes of both lists to be equal.

Since a list type can be represented as an infinite sum of tuples, I knew that the categorical version of this formula must involve a power series, or a polynomial functor:

$\mathbf{Set} \big(s, \sum_{n} \mathbf{Set}(b^n, t) \times a^n\big)$

but was unable to come up with an existential form for it.

Pickering, Gibbons, and Wu came up with a representation for traversals using profunctors that were cartesian, cocartesian, and monoidal at the same time, but the monoidal constraint didn’t fit neatly into the Tambara scheme:

class Profunctor p => Monoidal p where
  par   :: p a b -> p c d -> p (a, c) (b, d)
  empty :: p () ()

We’ve been struggling with this problem, when one of my students, Mario Román came up with the ingenious idea to make $n$ existential.

The idea is that a coend in the existential representation of optics acts like a sum (or like an integral—hence the notation). A sum over natural numbers is equivalent to the coend over the category of natural numbers.

At the root of all optics there is a monoidal action. For lenses, this action is given by “scaling”

$a \to a \times c$

For prisms, it’s the “translation”

$a \to a + c$

For grates it’s the exponentiation

$a \to a^c$

The composition of a prism and a lens is an affine transformation

$a \to c_0 + a \times c_1$

A traversal is similarly generated by a polynomial functor, or a power series functor:

$a \to \sum_n c_n \times a^n$

The key observation here is that there is a different object $c_n$ for every power of $a$ , which can only be expressed using dependent types in programming. For every multiplicity of foci, the residue is of a different type.

In category theory, we can express the whole infinite sequence of residues as a functor from the monoidal category $\mathbb{N}$ of natural numbers to $\mathbf{Set}$ . (The sum is really a coend over $\mathbb{N}$ .)

The existential version of a traversal is thus given by:

$\int^{c \colon [\mathbb{N}, \mathbf{Set}]} \mathbf{Set}\big(s, \sum_n c_n \times a^n\big) \times \mathbf{Set}\big( \sum_m c_m \times b^m, t\big)$

We can now use the continuity of the hom-set to replace the mapping out of a sum with a product of mappings:

$\int^{c \colon [\mathbb{N}, \mathbf{Set}]} \mathbf{Set}\big(s, \sum_n c_n \times a^n\big) \times \prod_m \mathbf{Set}\big( c_m \times b^m, t\big)$

and use the currying adjunction

$\int^{c \colon [\mathbb{N}, \mathbf{Set}]} \mathbf{Set}\big(s, \sum_n c_n \times a^n\big) \times \prod_m \mathbf{Set}\big( c_m, \mathbf{Set}( b^m, t)\big)$

The product of hom-sets is really an end over $\mathbb{N}$ , or a set of natural transformations in $[\mathbb{N}, \mathbf{Set}]$

$\int^{c \colon [\mathbb{N}, \mathbf{Set}]} \mathbf{Set}\big(s, \sum_n c_n \times a^n\big) \times [\mathbb{N}, \mathbf{Set}]\big( c_-, \mathbf{Set}( b^-, t)\big)$

and we can apply the Yoneda lemma to “integrate” over $c$ to get:

$\mathbf{Set}(s, \sum_n (\mathbf{Set}(b^n, t) \times a^n)\big)$

which is exactly the formula for traversals.

Once we understood the existential representation of traversals, the profunctor representation followed. The equivalent of Tambara modules for traversals is a category of profunctors equipped with the monoidal action parameterized by objects in $[\mathbb{N}, \mathbf{Set}]$ :

$\alpha_{c, \langle a, b \rangle} \colon p \langle a, b \rangle \to p\langle \sum_n c_n \times a^n, \sum_m c_m \times b^m \rangle$

The double Yoneda trick works for these profunctors as well, proving the equivalence with the existential representation.

Generalizations

As hinted in my blog post and formalized by Mitchell Riley, Tambara modules can be generalized to an arbitrary monoidal action. We have also realized that we can combine actions in two different categories. We could take an arbitrary monoidal category $\mathcal{M}$ , define its action on two categories, $\mathcal{C}$ and $\mathcal{D}$ using strong monoidal functors:

$F \colon \mathcal{M} \to [\mathcal{C}, \mathcal{C}]$

$G \colon \mathcal{M} \to [\mathcal{D}, \mathcal{D}]$

These actions define the most general existential optic:

$\mathbf{Optic} \langle s, t \rangle \langle a, b \rangle = \int^{m \colon \mathcal{M}} \mathcal{C}(s, F_m a) \times \mathcal{D}(G_m b, t)$

Notice that the pairs of arguments are heterogenous—e.g., in $\langle a, b \rangle$ , $a$ is from $\mathcal{C}$ , and $b$ is from $\mathcal{D}$ .

We have also generalized Tambara modules:

$\alpha_{m, \langle a, b \rangle} \colon p \langle a, b \rangle \to p \langle F_m a, G_m b\rangle$

and the Pastro Street derivation of the promonad. That lead us to a more general proof of isomorphism between the profunctor formulation and the existential formulation of optics. Just to be general enough, we did it for enriched categories, replacing $\mathbf{Set}$ with an arbitrary monoidal category.

Finally, we described some new interesting optics like algebraic and monadic lenses.

The Physicist’s Explanation

The traversal result confirmed my initial intuition from general relativity that the most general optics are generated by the analog of diffeomorphisms. These are the smooth coordinate transformations under which Einstein’s theory is covariant.

Physicists have long been using symmetry groups to build theories. Laws of physics are symmetric with respect to translations, time shifts, rotations, etc.; leading to laws of conservation of momentum, energy, angular momentum, etc. There is an uncanny resemblance of these transformations to some of the monoidal actions in optics. The prism is related to translations, the lens to rotations or scaling, etc.

There are many global symmetries in physics, but the real power comes from local symmetries: gauge symmetries and diffeomorphisms. These give rise to the Standard Model and to Einstein’s theory of gravity.

A general monoidal action seen in optics is highly reminiscent of a diffeomorphism, and the symmetry behind a traversal looks like it’s generated by an analytical function.

In my opinion, these similarities are a reflection of a deeper principle of compositionality. There is only a limited set of ways we can decompose complex problems, and sooner or later they all end up in category theory.

The main difference between physics and category theory is that category theory is more interested in one-way mappings, whereas physics deals with invertible transformations. For instance, in category theory, monoids are more fundamental than groups.

Here’s how categorical optics might be seen by a physicist.

In physics we would start with a group of transformations. Its representations would be used, for instance, to classify elementary particles. In optics we start with a monoidal category $\mathcal{M}$ and define its action in the target category $\mathcal{C}$ . (Notice the use of a monoid rather than a group.)

$F \colon \mathcal{M} \to [\mathcal{C}, \mathcal{C}]$

In physics we would represent the group using matrices, here we use endofunctors.

A profunctor is like a path that connects the initial state to the final state. It describes all the ways in which $a$ can evolve into $b$ .

If we use mixed optics, final states come from a different category $\mathcal{D}$ , but their transformations are parameterized by the same monoidal category:

$G \colon \mathcal{M} \to [\mathcal{D}, \mathcal{D}]$

A path may be arbitrarily extended, at both ends, by a pair of morphisms. Given a morphism in $\mathcal{C}$ :

$f \colon a' \to a$

and another one in $\mathcal{D}$

$g \colon b \to b'$

the profunctor uses them to extend the path:

$p \langle a, b \rangle \to p \langle a', b' \rangle$

A (generalized) Tambara module is like the space of paths that can be extended by transforming their endpoints.

$\alpha_{m, \langle a, b \rangle} \colon p \langle a, b \rangle \to p \langle F_m a, G_m b\rangle$

If we have a path that can evolve $a$ into $b$ , then the same path can be used to evolve $F_m a$ into $G_m b$ . In physics, we would say that the paths are “invariant” under the transformation, but in category theory we are fine with a one-way mapping.

The profunctor representation is like a path integral:

$\int_{p \colon \mathbf{Tam}} \mathbf{Set}( p \langle a, b \rangle, p \langle s, t \rangle)$

We fix the end-states but we vary the paths. We integrate over all paths that have the “invariance” or extensibility property that defines the Tambara module.

For every such path, we have a mapping that takes the evolution from $a$ to $b$ and produces the evolution (along the same path) from $s$ to $t$ .

The main theorem of profunctor optics states that if, for a given collection of states, $\langle a, b \rangle, \langle s, t \rangle$ , such a mapping exists, then these states are related. There exists a transformation and a pair of morphisms that are secretly used in the path integral to extend the original path.

$\int^{m \colon \mathcal{M}} \mathcal{C}(s, F_m a) \times \mathcal{D}(G_m b, t)$

Again, the mappings are one-way rather than both ways. They let us get from $s$ to $F_m a$ and from $G_m b$ to $t$ .

This pair of morphisms is enough to extend any path $p \langle a, b \rangle$ to $p \langle s, t \rangle$ by first applying $\alpha_m$ and then lifting the two morphisms. The converse is also true: if every path can be extended then such a pair of morphisms must exist.

What seems unique to optics is the interplay between transformations and decompositions: The way $m$ can be interpreted both as parameterizing a monoidal action and the residue left over after removing the focus.

Conclusion

For all the details and a list of references you can look at our paper “Profunctor optics, a categorical update.” It’s the result of our work at the Adjoint School of Applied Category Theory in Oxford in 2019. It’s avaliable on arXiv.

I’d like to thank Mario Román for reading the draft and providing valuable feedback.

Programming

The Para Construction

Parametric Optics

The PreLens Bicategory

Triple Tambara Modules

Tambara Representation

Bibliography

Introduction

Haskell Implementation

Existential Parametric Lens

Pre-Lenses

Pre-Neuron

Tambara Modules

TriLens

Training a Neural Network

Linear types

Linear lens: The existential form

Profunctor representation

van Laarhoven representation

Linear optics

Appendix: 1 Closed monoidal category in Haskell

Appendix 2: van Laarhoven representation

Appendix 3: My resource management curriculum

Disclaimers

Implementation hiding

Functors

Continuations

The Yoneda Lemma

Existential Types

Producer/Consumer

Co-Yoneda Lemma

Contravariant Consumers

Existential Lens

Type-Changing Lens

Other Optics

Profunctors

Profunctor Optics

Main Takeaways

Abstract

Motivation

Co-presheaves

Composition

Generalizations

Appendix

Motivation

Monoidal Action

Profunctor Representation

Counted Vectors and Trees

Existential Types

Polynomial Lens

Using the Lens

Example

Testing

Dependent optics

Dependent lens

Traversals

Traversals

Generalizations

The Physicist’s Explanation

Conclusion

Top Posts

License

Blogroll

Follow Me

Archives