I’m experimenting with new media so I prepared a one hour webinar on concurrency. You can’t really say much in an hour, so I’ll just give a broad overview of the domain without going into too much detail. Join me this Tuesday May 24, 2011 at 12pm PDT. The webinar is free, courtesy my employer, Corensic. You can preview the slides and, if you’re interested, register on the same page (you don’t have to fill out all the details).
Multicore
May 21, 2011
Concurrency Webinar
Posted by Bartosz Milewski under Concurrency, Multicore, Multithreading, Parallelism, Programming[7] Comments
May 20, 2011
Boostcon Day 4
Posted by Bartosz Milewski under Atomics, C++, Concurrency, Memory Model, Monads, Multicore, Multithreading, Programming1 Comment
I only went to one talk, not because the rest was not interesting, quite the contrary, but because I worked with Joel and Hartmut on rewriting Proto. I think we essentially got it. We have the exrpession monad implemented, my “compile” function turned out to be the equivalent of Proto transform, but with much more flexibility, expression extension produced a little Lambda EDSL with placeholders for arguments and even const terminals. It works like a charm. If you don’t know what I’m talking about, I promise to finish my blog series on monads in C++ real soon now.
The talk I went to was Chris Kohlhoff talking more about Asio, the asynchronous IO library. He was showing how the new features of C++11 make his code simpler, safer, and more flexible without too much effort. In particular he found move semantics extremely helpful in reducing (or, in some cases, eliminating) the need for memory allocation in steady state–an important property when running in an embedded system, for instance. But what I liked most was his approach to solving the inversion of control problem by implementing his own coroutines. Sure, he had to abuse C++ macros, but the code was actually much more readable and reflected the way we think about asynchronous calls.
The idea is that, with coroutines, you write your code in a linear way. You say “read socket asynchronously” and then yield. The flow of control exits the coroutine in the middle, and continues with other tasks. The trick is that the rest of the coroutine becomes your completion handler. When the async call completes, the coroutine is called again, but it starts executing right after the last yield. Your flow of control moves back and forth, but your code looks linear, instead of being fragmented into a bunch of handlers. It makes you wish coroutines were part of the language, as they are, for instance, in C#.
By the way, I caught Hans Boehm while he was waiting for the airport shuttle and asked questions about memory_order_relaxed. You know, the problem is, Can a relaxed load fetch an “out of thin air” value–a value that has never been written by anybody else? What I’m getting now is that in practice this will never happen, but it’s very hard to describe this requirement formally. In other words, Can a malicious chip manufacturer in cahoots with a compiler writer come up with a system that fulfills the letter of the C++ memory model and lets you fetch an out-of-thin-air value? I think the answer is yes, because the language of the Standard is purposely vague on this topic:
(29.3.11) [ Note: The requirements do allow r1 == r2 == 42 in the following example, with x and y initially zero:
// Thread 1: r1 = x.load(memory_order_relaxed); if (r1 == 42) y.store(r1, memory_order_relaxed); // Thread 2: r2 = y.load(memory_order_relaxed); if (r2 == 42) x.store(42, memory_order_relaxed);
However, implementations should not allow such behavior.—end note ]
May 18, 2011
Boostcon: Day 3
Posted by Bartosz Milewski under Atomics, C++, Concurrency, Memory Model, Multicore, Multithreading, Programming[8] Comments
Hans Boehm gave a keynote address about C++11’s support for concurrency. It was a nice overview of major features and, of course, the most interesting topic, atomics and weak atomics. The official story is that if you use locks and strong atomics, you get the DRF guarantee: If the program has no data races, it will behave in a sequentially consistent manner. How do you prove that you have no data races? You enumerate all possible interleavings, and if you can’t find one where two conflicting memory accesses happen next to each other, you’re golden. That’s more or less what Java memory model guarantees (and what Posix tried to standardize). However C++ offers the programmer a way to relax sequential consistency constraints without introducing data races. Now, if you spin it this way, it sounds like a really cool thing. Hey, look, my program is data-race free! And, get this, I don’t have to suffer sequential consistency! The natural question is, what does it buy me that the C++ Standard doesn’t treat “memory_order_relaxed” accesses as data races? I would like to hear that programs with weak atomics have well defined semantics, even if the semantics are so complex that proofs of correctness of even the simplest algorithms are non-existent. But as far as I know this is not “really” true (maybe “sort of” true?). I tried to get straight answers from Hans, but he chooses his words very carefuly, like a UN diplomat. I’ll see him again at the HotPar and I’lll press him some more.
Hans’s talk was followed by Tony Van Eerd’s presentation on lock-free programming. I liked Tony’s attitude, which was “Use Locks!” Indeed, you should look at lock-free algorithms as a last resort. He showed a few examples that were hair-raising. Even the simplest lock-free linked list is a challenge. It’s really hard to spot danger areas, like the ABA problem when the node you’re pointing at gets deallocated and reallocated when you’re not looking. Your CAS succeeds, because the addresses match, but your update ends up in the great bucket in the sky. The lock-free circular queue of integers with only one thread pushing and one thread popping turned out to be a mine field. Tony claimed that it should work with weak, relaxed memory order, atomics. But, of course, no formal proof is on the horizon. I stared at the code for minutes and it sort of made sense to me, but who knows? Hans stared at it some more and tentatively murmured that it’s probably okay. The bottom line: This is some really scary stuff.
Then I spent half a day with Hartmut and Joel: Me trying to understand Proto and they trying to understand monads. I think we’ve learned a lot from each other and the new formulation of Proto using monads is getting closer and closer. We have sort of nailed the definition of a monadic “function” in C++. I think we should call these things “hybrid” monads because they blend compile-time and runtime aspects of C++. Fascinating stuff!
April 26, 2011
Benign Data Races
Posted by Bartosz Milewski under Concurrency, Memory Model, Multicore, Multithreading, Programming[6] Comments
I am forking out my concurrency blogging to a new site, where I am actually paid to do it (who would have thought!). I promise to keep the same quality of posts as my readers came to expect from me. My first article there is about benign data races, an interesting and controversial topic.
I will still post programming-language and functional programming articles here. The next installment of the monad cycle is in the works. I’ll be talking about Haskell, C++ metaprogramming, and monads at this year’s Boostcon (May 15-20).
September 11, 2010
Beyond Locks: Software Transactional Memory
Posted by Bartosz Milewski under Concurrency, Multicore, Multithreading, Programming, Software Transactional Memory[28] Comments
1. “before every read we have to access our write set…” This is in case we have already written in this location during the current transaction. The write hasn’t been reflected in shared memory yet — it’s still sitting in our write set. We want to read this new value, not the original. So it’s not a conflict, but rather a consistency requirement.
2. “The lock and version number are sampled in one load.” Version number is combined with the lock bit in a single memory word, so it can be loaded in one instruction. Now we have a copy of version/lock locally and we can check it. If the test fails, we abort. If it succeeds, Traditional lock-based approach to concurrent programming is error prone, hard to debug, and almost impossible to scale.
In my previous post I gave a preview of how concurrent programming might evolve in the future, and the topic of Software Transactional Memory (STM) came up quite naturally. STM has the potential to replace locking with an easy to use, virtually fool-proof, scalable paradigm for concurrent access.
It’s true that STM has its problems; performance and integration with existing languages being the serious ones. The hope is that performance can be improved, especially if there’s some support in hardware, and that a new batch of concurrent languages will incorporate STM more smoothly.
In this post I won’t be elaborating on the superiority of STM over other paradigms but rather concentrate on how it works. I hope my explanation will be more approachable than academic papers.
STM in a Nutshell
Let’s analyze a very simple example, a singleton pattern in C++ (I chose C++ because it exposes the use of pointers):
Foo * getFoo() {
static Foo * pFoo = 0;
if (pFoo == 0) // <- read
pFoo = new Foo(); // <- write
return pFoo;
}
As you might know, this code doesn’t work correctly in a multithreaded environment. Let’s have a look at why, but from a slightly unusual angle. The statement:
if (pFoo == 0)
executes a memory read of the variable pFoo. The value that’s been read is usually stored in a register–in other words, is cached–at least until it’s compared with zero. Suppose that we read zero (a null pointer). We then proceed with the allocation and construction of the Foo object. We update the variable pFoo (a memory write) and return it to the caller.
The important thing is that the write to pFoo is only correct if the condition pFoo == 0 is maintained up to the moment when the new value is stored (we don’t even think of such subtleties in sequential programming).
But that condition may be broken by another thread storing its own creation in pFoo. It’s a classic data race, and its consequences may vary from a simple memory leak to a deadly memory fault (that might happen on some processors if the object Foo manages its own internal pointers). In general, it’s the gaps between logically related reads and writes that leave room for other threads to break our assumptions. If we could only concentrate those reads and writes into one atomic action, we’d be safe.
Let me propose a crazy solution: Before performing the write to pFoo, why don’t we re-check, or validate, our original read (assume that it’s still in the register). If the value in memory is still equal to the value in the register, we proceed with the write; otherwise we back off and try again.
Wait a moment! Aren’t we just postponing the problem? What about another thread messing with pFoo right between the read validation and the write? True, that is a problem, and we have to figure out a way to make the sequence read-validation/final-write atomic. But the beauty of this crazy approach is that it can be made universal. The code that does generic read verification may be compiled into the language runtime. It may be implemented once and for all, thoroughly tested, and used whenever concurrent access is needed.
All the programmer has to do is to inform the compiler that a logically related group of reads and writes must be done atomically; for instance, by enclosing the relevant code in the atomic block (not actual C++!):
Foo * getFoo() {
static Foo * pFoo = 0;
atomic {
if (pFoo != 0) // read
pFoo = new Foo(); // write(s), possibly reads
}
return pFoo;
}
Here’s what happens inside the atomic block (there are many variations of the algorithm but the idea is the same).
- First, a transaction is started–the runtime allocates a data structure containing two logs.
- Every memory read inside the atomic block is logged in a log called the read set.
- Every memory write, instead of going directly to memory, is written into the write set (there are also versions of STM that let the writes go through, to be undone if the transaction aborts).
- At the end of the
atomicblock the system attempts to commit the transaction. It does that by first verifying the read log and then performing the writes. (There is a very fine-grained system of locking in play, which I’ll describe shortly.) - If the read verification discovers a mismatch, the transaction is aborted and repeated from scratch, until it succeeds.
Some Details
There is one particular implementation of STM that’s been most widely accepted: Transactional Locking II (TL2), which I will summarize here.
Memory Layout
Imagine that for every single word of main memory you also have a separate data structure that stores the version number and a write lock for that word. How this can be done efficiently is an important implementation detail that I will explain later. For each memory word, its version number is initially set to zero and its lock is open.
Transaction
Now let’s start a transaction. We allocate a thread-local transaction object that has a read set and a write set, initially empty. We assign a version number to the transaction by (atomically) sampling the global “version clock” (it’s called a clock because it can only move forward). This will be our transaction’s read version number.
The compiler has conveniently instrumented all reads and writes inside the scope of the transaction (that is, in the atomic block). Each read adds an entry to our read set, storing the address of the word being read. Each write adds an entry to our write set, storing the address and the value to be written. The value in main memory is not changed at this point–the write is virtual.
Actually, before every read, we have to access our write set in case we have already written to that location. Moreover, we need to check that the location is not locked by another committing transaction, and that its version is less or equal to our transaction’s read version. This is why we need all those per-location locks and version numbers. If the location is locked or if its version number is larger than our current version, we abort the transaction and repeat the whole process again.
These checks are costly, and they are optimized to just a few instructions in the common case. So, for instance, the write-set check is implemented using a Bloom filter. Before every read we sample the corresponding lock and the version number (in one load, since it’s one word) and keep it for later. Then we check our write set using the Bloom filter. If we don’t find the corresponding entry, we just read the value directly from memory, otherwise we read it from our write log. Then we store the read address in our read set, and finally check the version number/lock that we have previously sampled. (On some processors, read barriers are required when accessing the locks.)
Going back to our singleton example, in Fig 1 you see the transaction corresponding right before committing. We have read the value of pFoo (directly from memory, since there was no entry in our write set yet) and logged the address of pFoo in our read set. We have checked that the version of pFoo, 6, was less than the version of our transaction, 8. We have also allocated a new Foo in memory. During the construction of Foo some two fields of Foo were (virtually) written and they have been saved in the write set together with the new value of pFoo (the pointer to the new Foo).
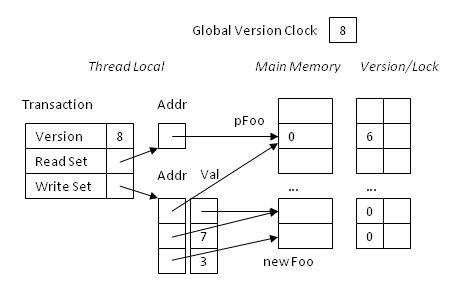
Fig 1. An STM transaction before commit. Every location in main memory has a corresponding version/lock entry. Both the read set and the write set have an entry for pFoo. The write set also stores the new value of pFoo, which is a pointer to the newly allocated Foo.
At commit time, we lock all our write locations (there are three of those) using the per-word locks. Since we might be racing with other transactions, we should be careful not to cause deadlocks. The simplest precaution is to use bounded spinlocks. If we fail to acquire any lock within a set timeout, we abort the transaction.
Committing the Transaction
Sequencing and Validation
During read set validation, we check the lock and the version number of each location that’s been read by our transaction. The problem is that this operation is not atomic (we don’t lock read locations). While we are validating, other transactions might modify the already validated locations. I’ll show you that it really doesn’t matter in the big scheme of things.
In the big scheme of things, there is a sequence of transactions, each making an atomic update. So our program’s memory switches from one consistent state to another. When, precisely, this jump occurs is called the “sequence point.” As I mentioned, the sequence point for each transaction is reached after the write set is locked but before the read set is validated.
Now imagine that we have two read locations, r1 and r2. We have validated r1 and, while we’re validating r2, a stray transaction commits a write to r1. What can be said about the sequence points of the two transactions? Our sequence point was set before we stated read validation. Since we have successfully validated r1, it hadn’t been locked by the stray transaction. It means that the other transaction’s sequence point must have been set after ours; and we don’t care about “future” transactions. All we are concerned about at this point is whether an earlier transaction, with an earlier sequence point (which is, however, greater than our read version), hasn’t overwritten those locations.
At this point we atomically increment and fetch the global version clock–this will be our transaction’s write version, not to be confused with the earlier read version. We haven’t committed the transaction yet but, if we commit it, this will be its official commit point, a.k.a. sequence point.
Now we can validate the read set at our leisure. We make sure that the read locations are not locked by another thread, and that their version numbers are still less or equal to our transaction’s read version. This is a slightly tricky point–see the sidebar.
In our example, the locks for pFoo and for the two fields inside the newly allocated Foo will be taken, the clock incremented to 9, and the read set validated.
The read set is small–just the location of the variable pFoo. It is not locked by another thread (although it’s locked by us, because it is also present in our write set), and the version number is still less than 8.
The final step is to commit the write set. Each location is updated and then unlocked. We also set the version number for each modified location to the write version of our transaction (the value of the version clock at our sequence point). In our case, we change the version number of pFoo from 6 to 9.
You might be wondering why we verify each read at least twice–once while executing the instrumented client code, and once during validation. After all, if we read the wrong version of the variable, the transaction will fail anyway during verification. The problem is that, after reading a bunch of inconsistent values, the client code might get into all kinds of trouble, including infinite loops or access violations. This used to be a major concern before TL2.
Reasons to Abort
Let’s consider what can go wrong in our example that would force us to abort (and retry).
- During the first read of
pFoo:- We find it locked. That could happen if another transaction is just committing its write to
pFoo. - It’s version number is greater than our transaction’s read version number. That could happen if another transaction had just committed its own write.
- We find it locked. That could happen if another transaction is just committing its write to
- During pre-commit locking, we find
pFoolocked by another transaction. (We let that transaction proceed.) - During read validation of
pFoo:- The location is locked by another transaction. (This can’t happen in our case because we have locked it ourselves.)
- Its version number is greater than our read version number. This could happen if another transaction committed its write to
pFooafter we have read it last.
You can easily convince yourself that in each case it really makes sense to abort the transaction. Moreover, when we retry the transaction, pFoo will have already been initialized by another thread. In that case the transaction will just breeze through, almost as fast as the lock-based implementation.
Optimizations
Note that during our transaction other non-conflicting transactions could have committed successfully. Each such transaction increments the version lock. This is why our write version could be arbitrarily larger than our read version. On the other hand, if the write version is just one unit larger that the read version, we know that we were alone, and we can skip the read validation altogether. In fact this is what would have happened in our example where the read version was 8 and the write version was 9.
Another great optimization is read-only transactions. Transactions that don’t perform any writes don’t have to log the reads. It’s enough that they perform the lock/version check at the point of each read. If all reads are successful, the transaction is done. It has seen a consistent state of memory.
It’s worth noting that atomic operations in TL2 are non-blocking. They are usually implemented using the CAS instruction (Compare and Swap). The locking of individual memory words is done using bounded spinlocks.
Conserving Memory
Let’s see how we can implement all the locks and version numbers without doubling or tripling our computer’s memory. To begin with, we can combine the lock with the version number in one word–a versioned lock. We only need one bit for a spinlock and we can stick it at the bottom of the version number, as long as we only use even version numbers.
The second trick is to use a reasonably sized table of versioned locks and hash all memory locations into that table. Since there will be many locations that map into the same lock, spurious aborts may happen. Notice however that spurious aborts have no impact on the semantics of the program. Aborted transactions will be retried until they commit. In practice such spurious conflicts happen reasonably rarely.
Performance
With the usual caveat that there are lies, damned lies, and benchmarks; the performance of STM clocks at about half the performance of hand-crafted locks (this is more or less the consensus number–see the interview with Peyton-Jones and Harris for confirmation). Which is not bad, considering all the instrumentation that goes into it. But if you have a program that spends 90% of its time concurrently inserting and removing items from a red-black tree, you might consider hiring a team of highly experienced programmers and testers to create a faster, lock-based, or even lock-free, solution. But take into account an important fact: STM is very fine grained. For instance, when you’re inserting an item into a tree, the STM transaction will only lock the nodes that you are actually modifying. STM will easily beat a solution that uses one global lock per whole tree. Per-node manual locking is hard to implement correctly because of the risk of deadlocks.
By its optimistic nature, STM performs best under low contention scenarios where the vast majority of transactions commit on the first try.
What’s Next?
Will performance problems interfere with a wider acceptance of STM? There is an interesting analogy between garbage collection (GC) and STM put forward by Dan Grossman. Historically, performance concerns were a major obstacle in the acceptance of GC until a general-purpose language, Java, adopted it as the memory management tool. If the analogy holds, the same will happen to STM and shared-memory concurrency.
STM has a permanent spot, and probably the best implementation, in Haskell (doesn’t it remind you of the relationship between Lisp and GC?). There’s been some STM activity in C++, Java, and other languages (see Bibliography) but, without language support, STM doesn’t offer enough bang for the buck in terms of safety and ease of use. That’s why I’m really excited about the use of STM in a batch of new high-performance languages, in particular in Chapel. Will Chapel become to STM what Java became to GC? Only time will tell.
I’ve been following the progress of the Chapel’s implementation of STM and talked to some of the developers. In distributed environments, STM can perform outstandingly. That’s because the overhead of STM read/write logging (which is done locally) is dwarfed by the usual distributed communication costs. The trick is to piggyback STM communications on top of remote reads and writes, which have to happen anyway. Chapel also has a chance to implement a type system that makes STM safer to use. I hope to discuss those options in a future post.
Bibliography
- Herlihy and Moss, Transactional Memory: Architectural Support for Lock-Free Data Structures
- Dice, Shalev, Shavit, Transactional Locking II
- Interview with Simon Peyton-Jones and Tim Harris about STM
- Harris, Fraser, Language Support for Lightweight Transactions–STM in Java
- TinySTM, a public domain implementation of STM for C and C++
- Deuce, a Java implementation of STM
- Bronson, Chafi, Olukotun, CCSTM: A Library-Based STM for Scala
- Harris, Marlow, Peyton Jones, Herlihy, Composable Memory Transactions–STM in Haskell.
- Sridharan, Vetter, Kogge, Scalable Software Transactional Memory for Global Address Space Architectures–STM in Chapel
May 11, 2010
Parallel Programming with Hints
Posted by Bartosz Milewski under .NET, C++, Concurrency, Haskell, Multicore, Multithreading, Programming[9] Comments
Wouldn’t it be nice to be able to write sequential programs and let the compiler or the runtime automatically find opportunities for parallel execution? Something like this is already being done on a micro scale inside processors. As much as possible, they try to execute individual instructions in parallel. Of course they have to figure out data dependencies and occasionally stall the pipeline or idle while waiting for a memory fetch. More sophisticated processors are even able to speculate–they guess a value that hasn’t been calculated or fetched yet and run speculative execution. When the value is finally available, they compare it with their guess and either discard or commit the execution.
If processors can do it, why can’t a language runtime do the same on a larger scale? It would solve the problem of effectively using all those cores that keep multiplying like rabbits on a chip.
The truth is, we haven’t figured out yet how to do it. Automatic parallelization is, in general, too complex. But if the programmer is willing to provide just enough hints to the compiler, the runtime might figure things out. Such programming model is called semi-implicit parallelism and has been implemented in two very different environments, in Haskell and in .NET. The two relevant papers I’m going to discuss are Runtime Support for Multicore Haskell and The Design of a Task Parallel Library.
In both cases the idea is to tell the compiler that certain calculations may be done in parallel. It doesn’t necessarily mean that the code will be executed in multiple threads–the runtime makes this decision depending on the number of cores and their availability. The important thing is that, other than providing those hints, the programmer doesn’t have to deal with threads or, at least in Haskell, with synchronization. I will start with Haskell but, if you’re not into functional programming, you may skip to .NET and the Task Parallel Library (and hopefully come back to Haskell later).
In Multicore Haskell
In Haskell, you hint at parallel execution using the par combinator, which you insert between two expressions, like this: e1 `par` e2. The runtime then creates a spark for the left hand side expression (here, e1). A spark is a deferred calculation that may be executed in parallel (in the .NET implementation a spark is called a task). Notice that, in Haskell, which is a lazy programming language, all calculations are, by design, deferred until their results are needed; at which point their evaluation is forced. The same mechanism kicks in when the result of a spark is needed–and it hasn’t been calculated in parallel yet. In such a case the spark is immediately evaluated in the current thread (thus forfeiting the chance for parallel execution). The hope is though that enough sparks will be ready before their results are needed, leading to an overall speedup.
To further control when the sparks are evaluated (whether in parallel or not), Haskell provides another combinator, pseq, which enforces sequencing. You insert it between two expressions, e1 `pseq` e2, to make sure that the left hand side, e1, is evaluated before the evaluation of e2 is started.
I’ll show you how to parallelize the standard map function (in C++ it would be called std::transform). Map applies a function, passed to it as the first argument, to each element of a list, which is passed to it as the second argument. As a Haskell refresher, let me walk you through the implementation of map.
map f [] = []
map f (x:xs) = y:ys
where y = f x
ys = map f xs
Map is implemented recursively, so its definition is split into the base case and the recursive case. The base case just states that map applied to an empty list, [], returns an empty list (it ignores the first argument, f).
If, on the other hand, the list is non-empty, it can be split into its head and tail. This is done through pattern matching–the pattern being (x:xs), where x matches the head element and xs the (possibly empty) tail of the list.
In that case, map is defined to return a new list, (y:ys) whose head is y and tail is ys. The where clause defines those two: y is the result of the application of the function f to x, and ys is the result of the recursive application of map to the tail of the list, xs.
The parallel version does the same (it is semantically equivalent to the sequential version), but it gives the runtime the opportunity to perform function applications in paralle. It also waits for the evaluation to finish.
parMap f [] = []
parMap f (x:xs) = y `par` (ys `pseq` y:ys)
where y = f x
ys = parMap f xs
The important changes are: y, the new head, may be evaluated in parallel with the tail (the use of the par combinator). The result, y:ys, is returned only when the tail part, ys, has been evaluated (the use of the pseq combinator).
The tail calculation is also split into parallel computations through recursive calls to parMap. The net result is that all applications of f to elements of the list are potentially done in parallel. Because of the use of pseq, all the elements (except for the very first one) are guaranteed to have been evaluated before parMap returns.
It’s instructive to walk through the execution of parMap step-by-step. For simplicity, let’s perform parMap on a two-element list, [a, b].
First we pattern-match this list to x = a and xs = [b]. We create the first spark for the evaluation of (y = f a) and then proceed with the evaluation of the right hand side of par, (ys `pseq` y:ys). Here ys = parMap f [b].
Because of the `pseq`, we must evaluate ys next. To do that, we call (parMap f [b]). Now the list [b] is split into the head, b, and the empty tail, []. We create a spark to evaluate y' = f b and proceed with the right-hand side, (ys' `pseq` y':ys').
Again, the `pseq` waits for the evaluation of ys' = parMap f []. But this one is easy: we apply the base definition of parMap, which returns an empty list.
Now we are ready to retrace our steps. The right hand side of the last `pseq` re-forms the list y':[]. But that’s the ys the previous `pseq` was waiting for. It can now proceed, producing y:(y':[]), which is the same as [y, y'] or [f a, f b], which is what we were expecting.
Notice complete absence of explicit synchronization in this code. This is due to the functional nature of Haskell. There’s no shared mutable state so no locking or atomic operations are needed. (More explicit concurrent models are also available in Haskell, using MVars or transactional memory.).
Task Parallel Library in .NET
It’s no coincidence that many ideas from Haskell end up in Microsoft languages. Many Haskell programmers work for Microsoft Research, including the ultimate guru, Simon Peyton Jones. The Microsoft Task Parallel Library (TPL) translates the ideas from Multicore Haskell to .NET. One of its authors, Daan Leijen, is a Haskell programmer who, at some point, collaborated with Simon Peyton Jones. Of course, a .NET language like C# presents a different set of obstacles to parallel programming. It operates on mutable state which needs protection from concurrent access. This protection (which, incidentally, is the hardest part of multithreaded programming) is left to the programmer.
Here’s the example of an algorithm in C# with hidden opportunities for parallel implementation. MatrixMult multiplies two matrices. It iterates over columns and rows of the result matrix. The value that goes at their intersection is calculated by the innermost loop.
void MatrixMult(int size, double[,] m1,double[,] m2, double[,] result)
{
for(int i = 0; i < size; i++){
// calculate the i'th column
for(int j = 0; j < size; j++){
result[i, j] = 0;
for(int k = 0; k < size; k++){
result[i, j] += m1[i, k] * m2[k, j];
}
}
}
}
Each column of the result could potentially be evaluated in parallel. The problem is, the size of the array and the number of processor cores might be unknown until the program is run. Creating a large number of threads when there are only a few cores may lead to a considerable slowdown, which is the opposite of what we want. So the goal of TPL is to let the programmer express the potential for parallel execution but leave it to the runtime to create an optimal number of threads.
The programmer splits the calculation into tasks (the equivalent of Haskell sparks) by making appropriate library calls; and the runtime maps those tasks into OS threads–many-to-one, if necessary.
Here’s how the same function looks with parallelization hooks.
void ParMatrixMult(int size, double[,] m1,double[,] m2, double[,] result)
{
Parallel.For(0, size, delegate(int i)
{
for(int j = 0; j < size; j++){
result[i, j] = 0;
for(int k = 0; k < size; k++){
result[i, j] += m1[i, k] * m2[k, j];
}
}
});
}
Because of clever formatting, this version looks very similar to the original. The outer loop is replaced by the call to Parallel.For, which is one of the parallelizing TPL functions. The inner loops are packed into a delegate.
This delegate is assigned to a task (the analog of Haskell spark) that is potentially run in a separate thread. Here the delegate is actually a closure–it captures local variables, size, m1, m2 and result. The latter is actually modified inside the delegate. This is how shared mutable state sneaks into potentially multi-threaded execution. Luckily, in this case, such sharing doesn’t cause races. Consider however what would happen if we changed the types of the matrices from double[,] to char[,]. Parallel updates to neighboring byte-sized array elements may inadvertently encroach on each other and lead to incorrect results. Programmer beware! (This is not a problem in Haskell because of the absence of mutable state.)
But even if the programmer is aware of potential sharing and protects shared variables with locks, it’s not the end of the story. Consider this example:
int sum = 0;
Parallel.For(0, 10000, delegate(int i)
{
if(isPrime(i)){
lock(this) { sum += i; }
}
});
The captured variable, sum is protected by the lock, so data races are avoided. This lock, however, becomes a performance bottleneck–it is taken for every prime number in the range.
Now consider the fact that, on a 4-core machine, we’ll be running 10000 tasks distributed between about 4 threads. It would be much more efficient to accumulate the sum in four local variables–no locking necessary–and add them together only at the end of the calculation. This recipe can be expressed abstractly as a map/reduce type of algorithm (a generalization of the C++ std::accumulate). The tasks are mapped into separate threads, which work in parallel, and the results are then reduced into the final answer.
Here’s how map/reduce is expressed in TPL:
int sum = Parallel.Aggregate(
0, 10000, // domain
0, // initial value
delegate(int i){ return (isPrime(i) ? i : 0) },
delegate(int x, int y){ return x+y; }
);
The first delegate, which is run by 10000 tasks, does not modify any shared state–it just returns its result, which is internally accumulated in some hidden local variable. The second delegate–the “reduce” part of the algorithm–is called when there’s a need to combine results from two different tasks.
The Place for Functional Programming
Notice that the last example was written in very functional style. In particular you don’t see any mutable state. The delegates are pure functions. This is no coincidence: functional programming has many advantages in parallel programming.
I’ve been doing a lot of multi-threaded programming in C++ lately and I noticed how my style is gradually shifting from object-oriented towards functional. This process is accellerating as functional features keep seeping into the C++ standard. Obviously, lambdas are very useful, but so is move semantics that’s been made possible by rvalue references, especially in passing data between threads. It’s becoming more and more obvious that, in order to be a good C++ programmer, one needs to study other languages. I recommend Haskell and Scala in particular. I’ll be blogging about them in the future.
Bibliography
- Simon Marlow, Simon Peyton Jones, and Satnam Singh, Runtime Support for Multicore Haskell
- Daan Leijen, Wolfram Schulte, and Sebastian Burckhardt, The Design of a Task Parallel Library
- A video introduction to Haskell by Simon Peyton Jones: Part I, Part II, together with the slides.
March 10, 2009
Futures done right
Posted by Bartosz Milewski under C++, Concurrency, Haskell, ML, Multicore, Programming[14] Comments
In my last post I criticized the C++0x implementation of futures for their lack of composability. I now feel obliged to show what I consider “the right way” to do futures.
I use the event library of Concurrent Caml (actually, its version distributed with OCaml) as my model. The ideas behind it are described in J. H. Reppy’s Ph.D. thesis, Higher-order concurrency.
Events and Futures
CML channels and events are more general than futures, but here I’ll concentrate on the subset of their functionality that can be used to implement futures. Below is a useful translation table between CML and C++. (I should add that CML channels, as opposed to C++ futures, are synchronous. In practice it doesn’t matter that much, since promise::set_value–corresponding to channel send–is usually called right before the thread exits.)
| CML | C++ |
|---|---|
| channel | promise |
| event | future |
| evt = receive chan | ftr = prom.get_future() |
| sync (send chan msg) (synchronous) | prom.set_value(msg) (asynchronous) |
| msg = sync evt | msg = ftr.get() |
| choose evt_lst | ??? |
| evt’ = wrap evt fun | ??? |
As you can see, C++ has no equivalents of choose and wrap. I will discuss those next.
choose
CML choose is a function that takes a list of events and creates a new composite event. When the program syncs on this event, it blocks until one of the listed events completes. The combination sync and choose is similar to Unix select or Windows WaitForMultipleObjects.
An example of the usefulness of choose is a situation when there is more than one algorithm to calculate a result, and the program runs them in parallel until the fastest one completes. Linear search, for instance, is faster for small sets than binary search. Instead of figuring out which one to use for each particular case, it might be cheaper (on a multicore) to run both and stop when the fist one is done.
What would choose look like in C++? One possibility is to implement it as a container object. You would push individual futures into it and then call get_future to obtain a composite future. Let me call this object future_or since it does the equivalent of logical OR for futures (the equivalent of AND is called a thread barrier).
unique_future<int> ftr1 = promise1.get_future(); unique_future<int> ftr2 = promise2.get_future(); future_or<int> orf; orf.push_back(std::move(ftr1)); orf.push_back(std::move(ftr2)); unique_future<int> compositeFut = orf.get_future(); ... int result = compositeFut.get();
Another possible implementation, in C++0x, would be to define a variadic template function future_choose. It would take a variable number of futures and return the composite future. The advantage of such an approach would be to let the compiler infer the types and the number of arguments automatically.
You probably noticed that future_or can only accept futures of one type (the same would be true about the function future_choose). For instance, to create a composite future that returns a string upon get, you must build it from other futures that also return a string (and not an int, for instance).
In principle, heterogeneous futures could be combined if they all returned different types through the same variant. Then, after a composite of variant-returning futures returns a variant, program logic would fork depending on the actual type inside the variant. This approach bypasses the static type system and is error prone. CML provides a more elegant solution using wrap.
wrap
The trick is to combine (wrap) a particular future with a function that processes its output. A future that returns an int is combined with a function that takes an int, etc. The result of this combination is a new future usually returning void.
When a wrapped future is synchronized (e.g., by calling wait), it executes the associated function, passing it the result returned by the original future. Just look at this example:
void handler(Foo const & foo); unique_future<Foo> fooFuture = prom.get_future(); // combine the future with a handler function unique_future<void> wrappedFuture = wrap_future(fooFuture, &handler); ... wrappedFuture.wait(); // at this point fooFuture has returned a Foo object // and the handler has been executed with that object.
There’s one thing worth mentioning: the compiler will assure type correctness of the arguments to wrap_future: the return type of the future must be compatible with the argument type of the function. Mismatch errors will be discovered at compile time. Compare this with the implementation using variants, which does not have this property.
Of course the usefulness of wrap really comes into play when you try to combine heterogeneous futures using future_choose. You just wrap each future with its own post-processing function (or callable object) and pass them all to future_choose. Wrapped futures are homogeneous–they all return void.
Here’s an example that uses C++0x lambdas (one of them being a closure):
unique_future<Foo> fooFuture = prom1.get_future();
unique_future<int> intFuture = prom2.get_future();
int sum = 0;
future<void> composite = future_choose(
wrap_future(fooFuture, [](Foo const & foo){foo.Commit();},
wrap_future(intFuture, [&sum](int i){sum += i;});
...
composite.wait();
Wrapped futures would be useful, e.g., in implementing a server that listens to several communication channels.
What about Haskell?
As I described in my earlier post, unlike CML, Haskell implements asynchronous message passing. The original Concurrent Haskell paper argued against choose. Later however Avik Chaudhuri was able to show that the CML event library can be implemented on top of asynchronous MVars. So there are no theoretical obstacles to asynchronous implementation of futures.
Final remarks
The equivalent of choose called future_select has been proposed for Boost and C++0x, but it was turned down.
Interestingly enough, Microsoft’s Task Parallel Library for .NET implements higher-order concurrency. They have ContinueWith for wrapping futures and WaitAny for choice. I can only assume that it’s easier to implement those on a virtual machine.
I also wonder whether it would be more productive to implement the equivalent of the CML channels and events in C++, and treat futures as a special case.
If you like this post, please vote for it on reddit.
Bibliography
- J. H. Reppy. Higher-order concurrency. PhD thesis, Cornell
University, 1992. Technical Report 92-1852. - Avik Chaudhuri. A Concurrent ML Library in Concurrent Haskell.
December 23, 2008
The Inscrutable C++ Memory Model
Posted by Bartosz Milewski under Atomics, C++, Concurrency, Memory Model, Multicore, Programming[14] Comments
In my last post I made a mistake of publishing a piece of code that used C++ weak atomics–which are part of the new C++ Memory Model. I qualified the post by saying that I had no proof of correctness, and the main purpose of it was to discourage the use of weak atomics. In a way the post was successful because it did prove that weak atomics are very tricky indeed. As was pointed out to me by Anthony and Dmitriy, my implementation was incorrect (I modified the post retroactively to make this point clear). Additionally, in his blog, Anthony published a proof of the algorithm posted by Dmitriy. And that’s when the fun started…
Before I describe what happened, let me give you a bird’s eye view of the C++ Memory Model.
The Model
The purpose of a memory model is to define the semantics of concurrent operations at an abstract level–independent of the platform on which the program is running. Essentially, one has to define in what order program statements may be executed, and what memory values may be observed. The basic memory model, the one used by Java, is based on sequential consistency. Program statements are executed in program order on each processor, and the actions of multiple threads are interleaved in some (global) order. A memory load can only see the value that was written last, according to this global order.
The C++ strong atomics (the default) follow this model.
It’s the weak atomics that are trouble. Weak atomics let the programmer specify memory ordering of loads and stores that is less than sequentially consistent. Unlike the sequentially consistent model, the model for weak atomics cannot be described in terms of a state machine (this was pointed out and criticized by Herb Sutter in his Prism proposal). Instead the model is formulated as a set of global constraints imposed on executions.
In a state-machine formulation, a step the program takes is based on previous history. The step doesn’t have to be uniquely defined–the machine may be non-deterministic. The execution may split into multiple branches. What is important, though, is that the step taken does not depend on the future of the execution.
This is not true in the weak-atomics model. The way to think about it is that, in a non-sequentially-consistent execution, the values seen by memory loads may come either from the past or from the future. A processor may speculate–make a guess at the values that have not been stored yet. A speculation may be discarded if the guess turns out to be wrong, or accepted if it was right. So the acceptability of a given execution can only be determined by looking at the whole execution, from start to end. Understandably, this makes any correctness proofs extremely tricky.
The Proof
The proposed implementation of the Peterson lock using weak atomics can be reduced to the following:
// Thread 0 zeroWants.save(true, memory_order_relaxed); r0 = victim.exchange(0, memory_order_acq_rel); r1 = oneWants.load(memory_order_acquire); // Thread 1 oneWants.save(true, memory_order_relaxed); r2 = victim.exchange(1, memory_order_acq_rel); r3 = zeroWants.load(memory_order_acquire);
(The memory_order_acquire directives in the two loads are needed for synchronization with the unlock part of the algorithm, which is not included here.)
The hardest part of the proof is to show mutual exclusion–it should be impossible for both threads to enter the critical section at the same time. In Peterson’s algorithm, the entrance to the critical section is predicated on the values loaded into r1 and r3. If both values are false, the algorithm is broken.
Let’s consider the situation when both threads try to acquire the lock for the first time. The values of zeroWants and oneWants are initially false, and the value of victim is zero. Is it possible for both loads (zeroWants and oneWants) to see the initial values, rather than the ones saved by the opposing thread? The short answer is yes, as long as there is no intervening inter-thread synchronization.
In this case, the only synchronization that may happen is between a store-release in one thread and the corresponding load-acquire in the other. For instance, if the load part of the exchange operation on victim in thread 0 sees the value written by the store part of the exchange in thread 1 (that is, r0 is equal to 1), than these two operations are in a “synchronizes-with” relationship. We can then establish the following chronology:
- The save of true to oneWants in T1 happens before the store of 1 to victim (part of exchange) in T1. This is guaranteed by program order.
- The store of 1 into victim in T1 happens before the load of victim in T0 (part of exchange). This is because r0 is 1 in this part of the proof.
- The load of victim in T0 happens before the load of oneWants in T0. This is guaranteed by program order.
Because the happens-before relation is transitive, we can conclude that the load of oneWants in T0 (item 3) must see the value stored in T1 (item 1), which is true, and therefore T0 won’t enter the critical section. So far so good.
That was the simple case. Here’s the controversial one: Both r0 and r2 are zero. In particular, it means that r0 came from the initial value of victim. What about r2? It could have come either from the exchange in T0 or from the initial value of victim (both are zero!). According to the memory model, we have to consider both cases!
If r0 came from the exchange in T1 then we can use the same reasoning as before to conclude that T1 cannot enter the critical section.
But if the source of the zero in r0 is the original value of victim then there is no synchronization between T0 and T1. Both threads can enter the critical section!
You might be thinking: Either the exchange in T1 comes first and the exchange in T2 must see its value, or the exchange in T2 comes first and the one in T1 must see its value–they can’t both see the original value. This just shows you how ingrained sequentially consistent thinking is. There is no meaning to “comes first” in the world of weak atomics. Two events may only be sequenced if they occur in the same thread, or there is a synchronization path between them. Here we are still at the stage of trying to establish whether the two exchanges are synchronized or not.
The Controversy
Let me spell it out: Both exchanges see the initial value of victim. Since they didn’t interact, there is no synchronizes-with relationship between them. Therefore we can’t establish any inter-thread chronology, and it’s perfectly possible for both threads to see the original values of zeroWants and oneWants.
// Thread 0 zeroWants.save(true, memory_order_relaxed); r0 = victim.exchange(0, memory_order_acq_rel); // sees initial value, 0 r1 = oneWants.load(memory_order_acquire); // sees initial value, false // Thread 1 oneWants.save(true, memory_order_relaxed); r2 = victim.exchange(1, memory_order_acq_rel); // sees initial value, 0 r3 = zeroWants.load(memory_order_acquire); // sees initial value, false
I had concluded that the implementation was broken, but I let Anthony defend his proof.
Here’s the argument he presented, based on the modification order of victim. The C++ memory model enforces global modification order for every memory location. The victim variable starts at zero and then is modified twice by the exchanges in T0 and T1. If thread T1 sees the original value, zero, of victim then the same exchange modifies it to one. The modification order is therefore (T1: 1, T0: 0). If we assume that an atomic exchange must always see the preceding value in the modification order, then we must conclude that the exchange in T0 must read 1. Therefore it synchronizes with the exchange in T1 and mutual exclusion is assured.
And here’s the clincher: The draft C++ Standard did not specify what value must be seen by the atomic exchange (or, more generally, by an atomic Read-Modify-Write operation). I confirmed that with Hans Boehm, who concluded that this apparent hole in the standard must be corrected.
The next draft of the Standard will say that a RMW operation must see the last value in the modification order of the memory object in question.
Only then the proof of correctness of the weak-atomics implementation of Peterson lock will be complete.
Conclusion
I had no idea what I was getting myself into when attempting to reason about C++ weak atomics. The theory behind them is so complex that it’s borderline unusable. It took three people (Anthony, Hans, and me) and a modification to the Standard to complete the proof of a relatively simple algorithm. Imagine doing the same for a lock-free queue based on weak atomics!
Hans, who was instrumental in creating the C++ memory model, hopes that weak atomics will be a stopgap measure until processor designers find more efficient ways of implementing sequential consistency. For now, it is strongly recommended to leave weak atomics to top experts whose numbers can be counted on the fingers of one hand.
I’m grateful to (in order of appearance) Anthony Williams, Dmitriy V’jukov, Hans Boehm, and others who contributed to this post.
December 1, 2008
C++ atomics and memory ordering
Posted by Bartosz Milewski under C++, Concurrency, Multicore, Programming | Tags: Atomics, C++ |[39] Comments
The question that’s been bugging me lately was: How does C++ make the use atomic variables both portable and efficient.
I knew how Java volatile worked–it enforced sequential consistency, which is not always the most efficient thing to do.
C++0x has atomic variables which also enforce sequential consistency when used in the default mode. Without special ordering annotations they work almost like Java’s volatile (interestingly, Java’s volatile doesn’t enforce atomicity–there is an atomic library in Java, though, which does).
However, C++ offers various degrees of relaxation of sequential consistency which, if used correctly, should produce more efficient code.
After studying a bit of the x86 memory model, I realized that some basic lock-free patterns (like the one in double-checked locking) will work without any fences. There should be a way of coding them in C++ such that, when compiled for the x86, no fences are produced. On the other hand, the same C++ code, when compiled for, let’s say, the alpha or the Power PC, should produce the necessary fencing.
To make things more interesting, there are some other algorithms, like the Peterson lock, which do require memory fences on the x86 (see my previous post). So it’s not just the matter of skipping all fencing.
I reduced my question to: How does one write portable code in C++ that results in just the right amount of fencing on the x86?
Specifying memory ordering in C++
The C++0x atomics library proposal underwent a lot of changes before it settled into its current shape. There is now a complete C++0x draft. It’s not an easy read so I’m grateful to Hans Boehm for clarifying some of the fine points.
Without further ado, this is how the publication safety pattern (the mother of all double-checked locking patterns) could be written in C++:
atomic<bool> ready = false; atomic<int> data = 0;
Thread 0:
data.store(1); ready.store(true);
Thread 1:
if (ready.load())
assert (data.load() == 1);
As you can see, atomic objects have methods store and load that are used for writing and reading underlying shared data. By default, these methods enforce sequential consistency. What it means is that this code has the same semantics as if it were written in Java using volatile variables. Consequently, on the x86, it will generate memory fences after each store.
But we know that these fences are not necessary for publication safety. How can we write code that would produce minimal fencing on the x86?
To make such fine tuning possible, the C++0x atomics library allows the programmer to specify ordering requirements for each load and store. I’ll explain various ordering options in a moment; for now let’s have a look at the optimized version of the publication pattern:
atomic<bool> ready = false; atomic<int> data = 0;
Thread 0:
data.store(1, memory_order_release); ready.store(true, memory_order_release);
Thread 1:
if (ready.load(memory_order_acquire))
assert (data.load(memory_order_acquire) == 1);
What’s important is that this code will work correctly on any major processor, but it will produce no fences on the x86.
Warning: Even if you know that your program will only ever run on an x86, you can’t remove the atomics and the ordering constraints from your code. They are still necessary to prevent the compiler from doing the reordering.
Fine-tuning memory ordering
Memory order can be specified using the following enumeration:
namespace std {
typedef enum memory_order {
memory_order_relaxed,
memory_order_consume,
memory_order_acquire,
memory_order_release,
memory_order_acq_rel,
memory_order_seq_cst
} memory_order;
}
The default for all operations on atomic variables is memory_order_seq_cst which, just like Java’s volatile, enforces sequential consistency. Other orderings are used to relax sequential consistency and often squeeze better performance from lock-free algorithms.
- memory_order_acquire: guarantees that subsequent loads are not moved before the current load or any preceding loads.
- memory_order_release: preceding stores are not moved past the current store or any subsequent stores.
- memory_order_acq_rel: combines the two previous guarantees.
- memory_order_consume: potentially weaker form of memory_order_acquire that enforces ordering of the current load before other operations that are data-dependent on it (for instance, when a load of a pointer is marked memory_order_consume, subsequent operations that dereference this pointer won’t be moved before it (yes, even that is not guaranteed on all platforms!).
- memory_order_relaxed: all reorderings are okay.
As I discussed before, the x86 guarantees acquire semantics for loads and release semantics for stores, so load(memory_order_acquire) and store(x, memory_order_release) produce no fences. So, indeed, our optimized version of the publication pattern will produce optimal assembly on the x86 (and I presume on other processors too).
But I have also shown before that the Peterson’s algorithm won’t work on the x86 without fencing. So it’s not enough to use just memory_order_acquire and memory_order_release to implement it. In fact, the problem with the Peterson lock was the possibility of reordering loads with stores. The weakest constraint that prevents such reordering is memory_order_acq_rel.
Now here the funny story begins. Without much thinking, I decided that just slapping memory_order_acq_rel on any of the writes would fix the problem. Here’s what I originally wrote:
[begin quote] The correct C++ code in this case is:
Peterson::Peterson() {
_victim.store(0, memory_order_release);
_interested[0].store(false, memory_order_release);
_interested[1].store(false, memory_order_release);
}
void Peterson::lock() {
int me = threadID; // either 0 or 1
int he = 1 – me; // the other thread
_interested[me].exchange(true, memory_order_acq_rel);
_victim.store(me, memory_order_release);
while (_interested[he].load(memory_order_acquire)
&& _victim.load(memory_order_acquire) == me)
continue; // spin
}
The ordering memory_order_acq_rel produces an mfence instruction on the x86. This fence will prevent the movement of the load of _interested[he] before the store to _interested[me], which could otherwise happen (and break the algorithm).[end quote]
You can read comments to this post–especially the ones by Anthony and Dmitriy, who made me eat crow. In short, the point is that the “acquire” part of memory_order_acq_rel has no meaning unless another thread writes to (“releases”) the same variable. Since only thread 0 writes to _interested[0] and only thread 1 one writes to _interested[1], this synchronization accomplished nothing (outside of the x86). Dmitriy’s implementation, which synchronizes on _victim, is correct (but I had to ask many questions before understanding Anthony’s proof of it).
Conclusion
What strikes me about this example is how non-trivial the reasoning behind this implementation was. I had to actually go through the x86 assembly to realize that I needed those and not some other ordering constraints (and I still got it wrong!). In comparison to that, the old fashioned assembly programming looks like a piece of cake.
| Any time you deviate from sequential consistency, you increase the complexity of the problem by orders of magnitude. |
Microsoft volatile
No, I’m not talking about the stock market. I mentioned before that C++ volatile has nothing to do with multithreading. This is not entirely true because some compiler vendors took the liberty to add non-standard semantics to volatile (out of pure desperation, since they had to support multi-processor code, and pre-0x C++ offered no help in this area). This new semantics, at least in the case of Microsoft compilers, did not include sequential consistency. Instead it guaranteed acquire and release semantics (which, on the x86, didn’t result in any fencing). So, although the publication pattern will work on a Microsoft compiler with volatile variables, the Peterson lock won’t! I thought that was an interesting piece of trivia.
November 11, 2008
Who ordered sequential consistency?
Posted by Bartosz Milewski under C++, Concurrency, Java, Multicore, Programming | Tags: Atomics, C++, Concurrency, Java, mfence, Multicore, volatile |[19] Comments
How does Java do it? Motivation for C++ programmers
Things like double-checked locking pattern and Peterson lock work out of the box in Java, as long as you declare all shared variables volatile. (Do not confuse Java volatile with C++ volatile–the latter has nothing to do with multithreading.) Obviously the Java compiler knows what kind of fences are necessary on relaxed memory architectures, including the x86. I thought it was worth looking at.
Why the sudden interest in Java? Because Java memory model is very relevant to C++0x. The keyword here is sequential consistency. Java enforces sequential consistency on all access to volatile variables. C++0x introduces atomic objects which, by default, also follow sequential consistency. So C++ atomics will, by default, behave almost exactly like Java volatile variables.
Also, why even bother studying the quirks of the x86? Can’t we just stick to locks and, occasionally, to default atomics and let the compiler/library writers worry about how they translate into fences? Absolutely!
This should be the end of the story, except that a lot of programmers seem to “know better.” They will try to optimize multithreaded algorithms and get into a world of trouble. So if you know anybody who might be tempted to write or optimize lock-free algorithms, read on.
Why the x86? Not only because it’s the most common chip, but also because its memory model is deceptively “normal.” It’s much more likely for programmers to attempt to play games with the x86 than, for instance, with the alpha. The rest of this post should serve as motivation to stay away form such games.
What is Sequential Consistency?
Sequential consistency is how we naturally think about multithreaded programs. It’s also how we think about the world. If A happens before B then it cannot be true that B happens before A. If one processor stores 1 in variable x, and another processor stores 1 in variable y, than either the sequence of events is:
- x flips to 1 and then y flips to 1, or
- y flips to 1 and then x flips to 1
(assume both are initially zero). Which sequence actually happened could be observed by a third processor, which loads both variables. If, for instance, it sees x == 1 and y == 0, it concludes that the write to x happened earlier. If it sees x == 0 and y == 1, it concludes that the write to y happened earlier (if it sees x == y, it can’t tell).
Now, in a sequentially consistent world, a fourth processor could not see the two events in a different order than what the third processor observed. We assume that, for each particular run of the program, there is a global sequence of events that is seen by all processors.
Of course, on multicore processors many things can happen simultaneously, and it usually doesn’t matter–except when memory access is involved. Sequentially consistent model assumes that there is a single switch between all processors and memory, and only one processor at a time can access it. This imaginary switch serves as the serialization point.
The x86 is not sequentially consistent
Welcome to the world of special relativity! Two observers (cores) might see two events (memory writes) in different order. Even on an x86.
The technical explanation is that, instead of one bus serializing all memory accesses, each core uses its own memory cache. Writes propagate from one cache to another with finite speed (measured in clock cycles). Reads snoop around the caches before going to shared memory. All this caching is done because a trip to main memory very expensive–hundreds of cycles.
I don’t care, says Java
The Java memory model requires that all access to shared volatile variables be sequentially consistent across all threads, even when they run on different cores. How do they enforce it?
The primary source for this kind of information is Doug Lea’s excellent The JSR-133 Cookbook for Compiler Writers.
Here’s the big picture: When Java is translated into bytecode, special codes are issued around volatile-variable access. These codes tell the Java runtime where memory fences should be inserted. The bytecodes are supposed to be processor independent; the fences are highly processor dependent. I’ll call the special bytecodes memory barriers as opposed to processor-specific memory fences. Memory barriers are inserted conservatively–the compiler assumes the most relaxed memory model (in other words, the bytecode has to run correctly on an alpha, whose memory model is so relaxed you’d think it was conceived in a hot tub).
Fences should go between memory accesses, so Java barriers are named after the kind of accesses (load or store) they separate. There is a LoadLoad barrier between volatile reads, LoadStore barrier between a read and a write, StoreLoad barrier between a write and a read, and StoreStore barrier between writes.
Here’s the first problem: the compiler can often only see one part of the pair. In that case it has to assume the worst and use the most restrictive barrier. Considering that, here are some of the cookbook rules:
- Issue a StoreStore barrier before each volatile store.
- Issue a StoreLoad barrier after each volatile store.
- Issue LoadLoad and LoadStore barriers after each volatile load.
That’s a lot of barriers! Fortunately, the compiler can optimize some of them away using dataflow analysis.
The next step is to run the bytecode on a particular processor (or compile it to native code). If the processor is an alpha, practically all Java barriers translate into some kind of fences. But if it’s an x86, all but the StoreLoad barriers are turned into no-ops. The StoreLoad barrier is either translated into an mfence or a locked instruction (lock xchg).
When executed on an x86, the barrier rules boil down to this one: Issue an mfence after each volatile store (or turn it into lock xchg).
Peterson lock on an x86 in Java
Figuring the details of the Peterson lock in Java was not easy. I’m grateful to Doug Lea for patiently explaining to me some of the gotchas. I am solely responsible for any mistakes though.
In my previous post I came to the conclusion that for Peterson lock to work on an x86, an mfence is needed. Here’s the relevant pseudo-code:
| Thread 0 | Thread 1 |
|---|---|
|
store(zeroWants, 1) mfence store(victim, 0) // Java puts another fence here r0 = load(oneWants) r1 = load(victim) |
store(oneWants, 1) mfence store(victim, 1) // Java puts another fence here r0 = load(zeroWants) r1 = load(victim) |
In Java, all three variables, zeroWants, oneWants, and victim, would be declared volatile. Using the x86 Java translation rules, that would mean putting an mfence after every store to these variables.
The fences after the writes to zeroWant and oneWant are just what the doctor ordered. Form my previous post we know why they are needed on an x86.
The mfence after the write to victim is something new though. It isn’t strictly necessary on an x86, but to see that you really have to analyze the whole algorithm–something that’s beyond capabilities of modern compilers.
My original (turns out, incorrect) reasoning was that no fence is needed between the write to victim and the subsequent read because, on an x86, reads and writes to the same location are never reordered. Well, that’s not the whole story because…
Intra-processor forwarding is allowed
Consider the following example from the x86 spec. Initially x == y == 0.
| Processor 0 | Processor 1 |
|---|---|
| mov [_x], 1 mov r1, [_x] mov r2, [_y] |
mov [_y], 1
mov r3, [_y] |
The result r2 == 0 and r4 == 0 is allowed.
Let’s analyze that. First of all, because reads and writes to the same location are never reordered, r1 and r3 must both be 1.
If r2 == 0, we would naturally conclude that the write to y at processor 1 hasn’t happened yet. It means: processor 1 hasn’t executed its code yet. When it does, it should see the earlier write to x (processor 0 saw it!). Guess what–sometimes it doesn’t.
The technical reason for this behavior is that the write to x is immediately visible at processor 0, before it propagates to processor 1. Similarly, the write to y is immediately visible at processor 1, before it propagates to processor 0. So it is possible for both processor to see each other’s writes delayed, even though they see their own writes immediately.
This result violates sequential consistency and therefore cannot be tolerated in Java. Hence the need for the mfence between the write to victim and the subsequent read of victim.
Gosh darn it! I want to optimize it!
Having said that, I must point out that, in this particular case, lack of sequential consistency is not a deal breaker. It’s okay for thread 0 of Peterson lock to read stale (local) value of victim, even if “in the meanwhile” thread 1 overwrote it. All it means is that some unnecessary spins might be performed. This doesn’t violate the lock principles and doesn’t lead to a deadlock as long as the new value of victim eventually reaches thread 0.
I’m pretty sure of this reasoning–at least at the time of this writing. However, I wouldn’t be totally surprised is somebody found a fault in it.
The bottom line is that even such an “obvious” optimization is not obviously correct. The proof of correctness of the Peterson lock is based on the assumption of sequential consistency. If we relax this assumption even slightly, we have to redo the whole proof.
Any volunteers?
