Homotopy Type Theory

Archived Posts from this Category

October 18, 2025

Modeling Identity Types

Previously: Identity Types.

Let me first explain why the naive categorical model of dependent types doesn’t work very well for identity types. The problem is that, in such a model, any arrow can be considered a fibration, and therefore interpreted as a dependent type. In our definition of path induction, with an arrow $d$ that makes the outer square commute, there are no additional constraints on $\rho$ :

So we are free to substitute $\text{refl} \colon A \to \text{Id}_A$ for $\rho$ , and use the identity for $d$ :

We are guaranteed that there is a unique $J$ that makes the two triangles commute. But these commutation conditions tell us that $J$ is the inverse of $\text{refl}$ and, consequently, $\text{Id}_A$ is isomorphic to $A$ . It means that there are no paths in $\text{Id}_A$ other than those given by reflexivity.

This is not satisfactory from the point of homotopy type theory, since the existence of non-trivial paths is necessary to make sense of things like higher inductive types (HITs) or univalence. If we want to model dependent types as fibrations, we cannot allow $\text{refl}$ to be a fibration. Thus we need a more restrictive model in which not all mappings are fibrations.

The solution is to apply the lessons from topology, in particular homotopy. Recall that maps between topological spaces can be characterized as fibrations, cofibrations, and homotopy equivalences. There usually are overlaps between these three categories.

A fibration that is also an equivalence is called a trivial fibration or an acyclic fibration. Similarly, we have trivial (acyclic) cofibrations. We’ve also seen that, roughly speaking, cofibrations generalize injections. So, if we want a non-trivial model of identity types, it makes sense to model $\text{refl}$ as a cofibration. We want different values $a \colon A$ to be mapped to different “paths” $\text{refl}(a) \colon \text{Id}_A$ , and we’d also like to have some non-trivial paths left over to play with.

We know what a path is in a topological space $A$ : it’s a continuous mapping from a unit interval, $\gamma \colon I \to A$ . In a cartesian category with weak equivalences, we can use an abstract definition of the object representing the space of all paths in $A$ . A path space object $P_A$ is an object that factorizes the diagonal morphism $\Delta = \pi \circ s$ , such that $s$ is a weak equivalence.

In a category that supports a factorization system, we can tighten this definition by requiring that $\pi$ be a fibration, defining a good path object; and $s$ be a cofibration (therefore a trivial cofibration) defining a very good path object.

The intuition behind this diagram is that $\pi$ produces the start and the end of a path, and $s$ sends a point to a constant path.

Compare this with the diagram that illustrates the introduction rule for the identity type:

We want $\text{refl}$ to be a trivial cofibration, that is a cofibration that’s a weak homotopy equivalence. Weak equivalence let us shrink all paths. Imagine a path as a rubber band. We fix one end and of the path and let the other end slide all the way back until the path becomes constant. (In the compact/open topology of $P_A$ , this works also for closed loops.)

Thus the existence of very good path objects takes care of the introduction rule for identity types.

The elimination rule is harder to wrap our minds around. How is it possible that any mapping that is defined on trivial paths, which are given by $\text{refl}$ over the diagonal of $A \times A$ , can be uniquely extended to all paths?

We might take a hint from complex analysis, where we can uniquely define analytic continuations of real function.

In topology, our continuations are restricted by continuity. When you are lifting a path in $A$ , you might not have much choice as to which value of type $D(a)$ to pick next. In fact, there might be only one value available to you — the “closest one” in the direction you’re going. To choose any other value, you’d have to “jump,” which would break continuity.

You can visualize building $J(a, b, p)$ by growing it from its initial value $J(a, a, \text{refl}(a)) = d(a)$ . You gradually extend it above the path $p$ until you reach the point directly above $b$ . (In fact, this is the rough idea behind cubical type theory.)

A more abstract way of putting it is that identity types are path spaces in some factorization system, and dependent types over them are fibrations that satisfy the lifting property. Any path from $a$ to $b$ in $\text{Id}_A$ has a unique lifting $J$ in $D$ that starts at $d(a)$ .

This is exactly the property illustrated by the lifting diaram, in which paths are elements of the identity type $\text{Id}_A$ :

This time $\text{refl}$ is not a fibration.

The general framework, in which to build models of homotopy type theory is called a Quillen model category, which was originally used to model homotopies in topological spaces. It can be described as a weak factorization system, in which any morphism can be written as a trivial cofibration followed by a fibration. It must satisfy the unique lifting property for any square in which $i$ is a cofibration, $p$ is a fibration, and one of them is a weak equivalence:

The full definition of a model category has more moving parts, but this is the gist of it.

We model dependent types as fibrations in a model category. We construct path objects as factorizations of the diagonal, and this lets us define non-trivial identity types.

One of the consequences of the fact that there could be multiple identity paths between two points is that we can, in turn, compare these paths for equality. There is, for instance, an identity type of identity types $\text{Id}_{\text{Id}_A(a, b)}$ . Such iterated types correspond to higher homotopies: paths between paths, and so on, ad infinitum. The structure that arises is called a weak infinity groupoid. It’s a category in which every morphism has an inverse (just follow the same path backwards), and category laws (identity or associativity) are satisifed up to higher morphisms (higher homotopies).

September 22, 2025

Identity Types

Posted by Bartosz Milewski under Category Theory, Homotopy, Homotopy Type Theory | Tags: Category Theory, Homotopy, HoTT, Identity Type |
[2] Comments

Previously: Models of (Dependent) Type Theory.

There is a deep connection between mathematics and programming. Computer programs deal with such mathematical objects as numbers, vectors, monoids, functors, algebras, and many more. We can implement such structures in most programming languages. For instance, here’s the definition of natural numbers in Haskell:

data Nat where
  Z :: Nat           -- zero
  S :: Nat -> Nat    -- successor

There is a problem, though, with encoding the laws that they are supposed to obey. These laws are expressed using equalities. But not all equalities are created equal. Take, for instance, this definition of addition:

plus :: Nat -> Nat -> Nat
plus Z n = n
plus (S n) m = S (plus n m)

The first clause tells us that $0 + n$ is equal to $n$ . This is called definitional equality, since it’s just part of the definition. However, if we reverse the order of the addends and try to prove $n + 0 = n$ , there is no obvious shortcut. We have to prove it the hard way! This second type of equality is called propositional.

In traditional mathematics equality is treated as a relation. Two things are either equal or not. In type theory, on the other hand, equality is a type. It’s a type of proofs of equality. When you postulate that two things are equal, you specify the type of proofs that you are willing to accept.

Equality is a dependent type, because it depends on the values that are being compared. For a pair of values of the type $A$ , the identity (or equality) type is denoted by $\text{Id}_A$ :

$\frac{a, b \colon A}{\text{Id}_A (a, b) \colon \text{Type}}$

(In this notation, assumptions are listed above the horizontal line.)

You’ll also see $\text{Id}_A(a, b)$ written as $a =_A b$ , or even $a = b$ , if the type $A$ is obvious from the context.

When two values are not equal, this type is uninhabited. Otherwise it’s inhabited by proofs, or witnesses, of equality. This is consistent with the propositions as types interpretation of type theory.

For the identity type to be useful, we have to have a way to populate it with values — proofs of equality. We do that by providing an introduction rule:

$\frac{a \colon A}{\text{refl}(a) \colon \text{Id}_A(a, a)}$

The constructor $\text{refl}$ generates a witness to the obvious fact that, for every $a$ , $a = a$ . Here, $\text{refl}$ is the abbreviation of reflexivity.

At first sight it doesn’t seem like we have gained anything by turning equality into a type. Indeed, if $\text{refl}$ were the only inhabitant of $\text{Id}_A$ , we’d just buy ourselves a lot of headaches for nothing. The trouble is that, if there is a type $\text{Id}_A(a, b)$ , then there’s also a type $\text{Id}_{\text{Id}_A(a,b)}$ (type of equality of proofs of equality), and so on, ad infinitum. This used to be a bane of Martin Löf type theory, but it became a bounty for Homotopy Type Theory. So let’s imagine that the identity type may have non-trivial inhabitants. We’ll call these inhabitants paths. The trivial paths generated by $\text{refl}$ are degenerate do-nothing loops.

But first, let’s consider the identity elimination rule: the mapping out of the identity type. What data do we need to provide in order to define a function from a path $p \colon \text{Id}_A(x, y)$ to some type $D$ ? In full generality, $D$ should be a dependent type family parameterized by the path $p$ as well as its endpoints $x$ and $y$ :

$x, y \colon A, \; p \colon \text{Id}_A (x, y) \vdash D(x, y, p) \colon \text{Type}$

Our goal is to define a $D$ -valued mapping $J$ that works for any path in $A$ :

$x, y \colon A, \; p \colon \text{Id}_A(x, y) \vdash J(x, y, p) \colon D(x, y, p)$

The trick is to realize that there is only one family of constructors of the identity type, $\text{refl}(a)$ , so it’s enough to specify how $J$ is supposed to act on it. We do this by providing a dependent function $d$ (a dependent function is a function whose return type depends on the value of its argument):

$a \colon A \vdash d(a) \colon D(a, a, \text{refl}(a))$

This is very similar to constructing a mapping out of a Boolean by specifying its action on the two constructors, $\text{True}$ and $\text{False}$ . Except that here we have a whole family of constructors $\text{refl}(a)$ parameterized by $a$ .

This is enough information to uniquely determine the action of $J$ on any path, provided it agrees with $d$ along $\text{refl}$ :

$J(a, a, \text{refl}(a)) = d(a)$

This procedure for defining mappings out of identity types is called path induction.

Categorical Model

We’ll build a categorical interpretation of identity types making as few assumptions as possible. We’ll model $\text{Id}_A$ as a fibration:

$\text{Id}_A \xrightarrow{\pi} A \times A$

The introduction rule asserts the existence of the arrow:

$A \xrightarrow{\text{refl}} \text{Id}_A$

For any given $a \colon A$ , this arrow selects a diagonal element of the identity type, $\text{Id}_A(a, a)$ . When projected down to $A \times A$ using $\pi$ , it lands on the diagonal of $A \times A$ . In a cartesian category, the diagonal is defined by the arrow $\Delta \colon A \to A \times A$ , so we have:

$\Delta = \pi \circ \text{refl}$

In other words, there is a factorization of the diagonal arrow.

The elimination rule starts with defining a dependent type $D$ , which can be modeled as a fibration $\rho$ :

$D \xrightarrow{\rho} \text{Id} \xrightarrow{\pi} A \times A$

We provide a dependent function $d$ , which is interpreted as an arrow $d : A \to D$ that maps $a$ to an element $d(a)$ of $D(a, a, \text{refl}(a))$ . So, when projected back to $\text{Id}_A$ using $\rho$ , it produces the same element as $\text{refl}(a)$

$\rho \circ d = \text{refl}$

Given these assumptions, there exists a mapping:

$x, y \colon A, p \colon \text{Id}_A(x, y) \vdash J(x, y, p) \colon D(x, y, p)$

which is interpreted as a section $\text{Id}_A \to D$ . The section condition is:

$\rho \circ J = id_{\text{Id}_A}$

This mapping is unique if we assume that it agrees with $d$ when restricted to $\text{refl}$ :

$J \circ \text{refl} = d$

Consequently, we can illustrate the path induction rule using a single commuting diagram:

If the outer square commutes then there is a unique diagonal arrow that makes the two triangles commute. The similarity to the lifting property of homotopy theory is not accidental, as we’ll see next.

Next: Modeling Identity Types.

September 5, 2025

Models of (Dependent) Type Theory

Posted by Bartosz Milewski under Category Theory, Functional Programming, Homotopy, Homotopy Type Theory, Type System | Tags: Category Theory, Dependent Types, Type Theory |
Leave a Comment

Previously: (Weak) Factorization Systems.

It’s been known since Lambek that typed lambda calculus can be modeled in a cartesian closed category, CCC. Cartesian means that you can form products, and closed means that you can form function types. Loosely speaking, types are modeled as objects and functions as arrows.

More precisely, objects correspond to contexts— which are cartesian products of types, with the terminal object representing the empty context. Arrows correspond to terms in those contexts.

Mathematicians and computer scientist use special syntax to formalize type theory that is used in lambda calculus. For instance a typing judgment:

$\vdash A \colon \text{Type}$

states that $A$ is a type. The turnstile symbol is used to separate contexts from judgments. Here, the context is empty (nothing on the left of the turnstile). Categorically, this means that $A$ is an object.

A more general context $\Gamma$ is a product of objects $A_1 \times A_2 \times ...$ . The judgment:

$\Gamma \vdash A \colon \text{Type}$

tells us that the type $A$ may depend on other types $A_1 \times A_2 \times ...$ , in which case $A$ is a type constructor. The canonical example of a type constructor is a list.

A term $t$ of type $A$ in some context $\Gamma$ is written as:

$\Gamma \vdash t \colon A$

We interpret it as an arrow from the cartesian product of types that form $\Gamma$ to the object $A$ :

$\Gamma \xrightarrow{t} A$

Things get more interesting when we allow types to not only depend on other types, but also on values. This is the real power of dependent types à la Martin-Löf.

For instance, the judgment:

$a \colon A \vdash B(a) \colon \text{Type}$

defines a single-argument type family. For every argument $a$ of type $A$ it produces a new type $B(a)$ . The canonical example of a dependent type is a counted vector, which encodes length (a value of type $\mathbb N$ ) in its type.

Categorically, we model a type family as a fibration given by an arrow $\pi \colon B \to A$ . The type $B(a)$ is a fiber $\pi^{-1} a$ .

In the case of counted vectors, the projection gives the length of the vector.

In general, a type family may depend on multiple arguments, as in:

$a_1 \colon A_1, a_2 \colon A_2, ... , a_n \colon A_n \vdash B(a_1, a_2, ..., a_n) \colon \text{Type}$

Here, each type in the context may depend on the values defined by its predecessor. For instance, $A_2$ may depend on $a_1$ , $A_3$ may depend on $a_1$ and $a_2$ , and so on.

Categorically, we model such a judgment as a tower of fibrations:

$B \xrightarrow{\pi_n} A_n ... \xrightarrow{\pi_2} A_2 \xrightarrow{\pi_1} A_1$

Notice that the context is no longer a cartesian product of types but rather an ordered series of fibrations.

A term in a dependently typed system has to satisfy an additional condition: it has to map into the correct fiber. For instance, in the judgment:

$a \colon A \vdash t(a) \colon B(a)$

not only $t$ depends on $a$ , but so does the type $B(a)$ . If we model $t$ as an arrow $A \to B$ , we have to make sure that $t(a)$ is projected back to $a$ . Categorically, we call such maps sections:

$\pi \circ t = id_A$

In other words, a section is an arrow that is a right inverse of a projection, .

Thus a well-formed vector-valued term produces, for every $n \colon \mathbb N$ , a vector of lenght $n$ .

In general, a term:

$a_1 \colon A_1, a_2 \colon A_2, ... , a_n \colon A_n \vdash t \colon B$

is interpreted as a section $A_n \xrightarrow{t} B$ of the projection $\pi_n$ .

At this point one usually introduces the definitions of dependent sums and products, which requires the modeling category to be locally cartesian closed. We’ll instead concentrate on the identity types, which are closely related to homotopy theory.

Next: Identity Types.

June 20, 2025

(Weak) Homotopy Equivalences

Posted by Bartosz Milewski under Category Theory, Homotopy, Homotopy Type Theory, Topology | Tags: Category Theory, Homotopy, math, Topology |
Leave a Comment

Previously: Fibrations and Cofibrations.

In topology, we say that two shapes are the same if there is a homeomorphism– an invertible continuous map– between them. Continuity means that nothing is broken and nothing is glued together. This is how we can turn a coffe cup into a torus. A homeomorphism, however, won’t let us shrink a torus to a circle. So if we are only interested in how many holes the shapes have, we have to relax our notion of equivalence.

Let’s go back to the definition of homeomorphism. It is defined as a pair of continuous functions between two topological spaces, $f \colon X \to Y$ and $g \colon Y \to X$ , such that their compositions are identity maps, $f \circ g = id_Y$ and $g \circ f = id_X$ , respectively.

If we want to allow for extreme shrinkage, as with a (solid) torus shrinking down to a circle, we have to relax the identity conditions.

A homotopy equivalence is a pair of continuous functions, but their compositions don’t have to be equal to identities. It’s enough that they are homotopic to identities. In other words, it’s possible to create an animation that transforms one to another.

Take the example of a line $\mathbb R$ and a point. The point is a trivial topological space where only the whole space (here, the singleton $\{*\}$ ) and the empty set are open. $\mathbb R$ and $\{*\}$ are obviously not homeomorphic, but they don’t have any holes, so they should be homotopy equivalent.

Indeed, let’s construct the equivalence as a pair of constant functions: $f \colon x \mapsto *$ and $g \colon * \mapsto 0$ (the origin of $\mathbb R$ ). Both are continuous: The pre-image $f^{-1} \{ * \}$ is the whole real line, which is open. The pre-image $g^{-1}$ of any open set in $\mathbb R$ is $\{*\}$ , which is also open.

The composition $f \circ g \colon * \mapsto *$ is equal to the identity on $\{*\}$ , so it’s automatically homotopic to it. The interesting part is the composition $g \circ f \colon x \mapsto 0$ , which is emphatically not equal to identity on $\mathbb R$ . We can however construct a homotpy between the identity and it. It’s a function that interpolates between them:

$h \colon \mathbb R \times I \to \mathbb R$

$h (x, 0) = id_{\mathbb R} x = x$

$h(x, 1) = (g \circ f) x = 0$

( $I$ is the unit interval $[0, 1]$ .) Such a function exists:

$h (x, t) = (1 - t) \,x$

When a space is homotopy equivalent to a point, we say that it’s contractible. Thus $\mathbb R$ is contractible. Similarly, n-dimensional spaces, $\mathbb R^n$ , as well as n-dimensional balls are all contractible. A circle, however, is not contractible, because it has a hole.

Another way of looking for holes in spaces is by trying to shrink loops. If there is a hole inside a loop, it cannot be continuously shrunk to a point. Imagine a loop going around a circle. There is no way you can “unwind” it without breaking something. In fact, you can have loops that wind n times around a circle. They can’t be homotopied into each other if their winding numbers are different.

In general, paths in a topological space $X$ , i.e. continuous mappings $\gamma \colon I \to X$ , naturally split into equivalence classes with respect to homotopy. Two paths, $\gamma$ and $\gamma'$ , sharing the same endpoints are in the same class if there is a homotopy between them:

$h \colon I \times I \to X$

$h (0, t) = \gamma t$

$h (1, t) = \gamma' t$

Moreover, two paths can be composed, as long as the endpoint of one coincides with the start point of the other (after performing appropriate reparametrizations).

There is a unit of such composition, a constant path; and every path has its inverse, a path that traces the original but goes in the opposite direction.

It’s easy to see that path composition induces a groupoid structure on the set of equivalence classes of paths. A groupoid is a category in which every morphism (here, path) is invertible. This particular groupoid is called the fundamental groupoid of the topological space $X$ .

If we pick a base point $x_0$ in $X$ , the paths that start and end at this point form closed loops. These loops then form a fundamental group $\pi_1(X, x_0)$ .

Notice that, as long as there is a path $\gamma$ from $x_0$ to $x_1$ , the fundamental groups at both points are isomorphic. This is because every loop $l$ at $x_1$ induces a loop at $x_0$ given by the concatenation $l' = \gamma^{-1} \circ l \circ \gamma$ .

So there is essentially a single fundamental group for the whole space, as long as $X$ is path-connected, i.e., it doesn’t split into multiple disconnected chunks.

Going back to our example of a circle, its fundamental group is the group of integers $\mathbb Z$ with addition. All loops that wind n-times around the circle in one direction correspond to the integer n.

Negative integers correspond to loops winding in the opposite direction. If you follow an n-loop with an m-loop, you get an (m+n)-loop. Zero corresponds to loops that can be shrunk to a point.

To tie these two notions of hole-counting together, it can be shown that two spaces that are homotopy equivalent also have the same fundamental groups. This makes sense, since equivalent spaces have the same holes.

Not only that, they also have the same higher homotopy groups (as long as both are path-connected).

We define the n-th homotopy group by replacing simple loops (which are homotopic to a circle, or a 1-dimensional sphere) with n-dimensional spheres. Attempts at shrinking those may detect higher-dimensional holes.

For instance, imagine an Earth-like ball with it’s inner core scooped out. Any 1-loop inside its bulk can be shrunk to a point (it will glide off the core). But a 2-sphere that envelops the core cannot be shrunk.

In fact such a 2-sphere can be wrapped around the core an arbitrary number of times. In math notation, we say:

$\pi_2 (B^3 \setminus \{ 0 \}) = \mathbb Z$

Corresponding to these higher homotopy groups there is also a higher homotopy groupoid, in which there are invertible paths, surfaces between paths, volumes between surfaces, etc. Taken together, these form an infinity groupoid. It is exactly the inspiration behind the infinity groupoid in homotopy type theory, HoTT.

Spaces that are homotopy equivalent have the same homotopy groups, but the converse is not true. There are spaces that are not homotopy equivalent even though they have the same homotopy groups. This is why a weaker version of equivalence was introduced.

A map between topological spaces is called a weak homotopy equivalence if it induces isomorphisms between all homotopy groups.

There is a subtle difference between strong and weak equivalences. Strong equivalence can be broken by a local anomaly, like in the following example: Take $X = \{0, 1, 2, ... \}$ , the set of natural numbers in which every number is considered an open set. Take $Y = \{ 0 \} \cup \{ 1, \frac{1}{2}, \frac{1}{3}, ... \}$ with the topology inherited from the real line.

The singleton set $\{ 0 \}$ in $Y$ is the obstacle to constructing a homeomorphism or a homotopy equivalence between $X$ and $Y$ . That’s because it is not open (there is no open set in $\mathbb R$ that contains it and nothing else). However, it’s impossible to have a non-trivial loop that would contain it, so $X$ and $Y$ are weakly equivalent.

Grothendieck conjectured that the infinity groupoid captures all information about a topological space up to weak homotopy equivalence.

Weak equivalences, together with fibrations and cofibrations, form the foundation of weak factorization systems and Quillen model categories.
Next: (Weak) Factorization Systems.

May 30, 2025

Fibrations and Cofibrations

Posted by Bartosz Milewski under Category Theory, Homotopy, Homotopy Type Theory, Topology | Tags: Category Theory, Cofiber, Cofibration, Fibration, Homotopy, Topology |
1 Comment

Previously: Subfunctor Classifier.

We are used to thinking of a mapping as either being invertible or not. It’s a yes or no question. A mapping between sets is invertible if it’s both injective and surjective. It means that it never merges two elements into one, and it covers the whole target set.

But if you are willing to look closer, the failures of invertibility are a whole fascinating area of research. Things get a lot more interesting if you consider mapping between topological spaces, which have to skillfully navigate around various holes and tears in the target space, and shrink or glue together parts of the source space. I will be glossing over some of the topological considerations, concentrating on the big-picture intuitions (both culinary and cinematographic).

Fibrations

In what follows, we’ll be considering a function $p \colon E \to B$ . We’ll call $p$ a projection from the total set $E$ to the base set $B$ .

Let’s start by considering the first reason for a failure of invertibility: multiple elements being mapped into one. Even though we can’t invert such a mapping, we can use it to fibrate the source $E$ .

To each element $y \in B$ we’ll assign a fiber, the set of elements of $E$ that are mapped to $y$ . By abuse of notation, we call such a fiber $p^{-1} y$ :

$p^{-1} y = \{ x |\; p x = y \}$

For some $y$ ‘s, this set may be empty $\emptyset$ ; for others, it may contain lots elements.

Notice that $p$ is an isomorphism if and only if every fiber is a singleton set. This property gives rise to a very useful definition of equivalence in homotopy type theory, where we ask for every fiber to be contractible.

A set-theoretic union of all fibers reconstructs the total set $E$ .

Things get more interesting when we move to topological spaces and continuous functions. To begin with, we can define a path in $B$ as a continuous mapping from the unit interval $I = [0, 1]$ to $B$ .

$\gamma \colon I \to B$

We can then ask if it’s possible to lift this path to $E$ , that is to construct $\tilde{\gamma} \colon I \to E$ that lies above $\gamma$ . To do this, we pick the starting point $e \in E$ that lies above the starting point of $\gamma$ , that is $p \,e = \gamma \,0$ .

This setup can be summarized in the commuting square:

The lifting $\tilde{\gamma}$ is then the diagonal arrow that makes both triangles commute:

It’s helpful to imagine a path as a trajectory of a point moving through a topological space. The parameter $t \in I$ is then interpreted as time.

In homotopy theory we generalize this idea to the movement, or deformation, of arbitrary shapes, not just points.

If we describe such a shape as the image of some topological space $X$ , its deformation is a mapping $h \colon X \times I \to B$ . Such potentially “fat” paths are called homotopies. In particular, if we replace $X$ by a single point, we recover our “thin” paths.

A homotopy lifting property is expressed as the existence of the diagonal function $\tilde h$ in this commuting square, such that the resulting triangles commute:

In other words, given a homotopy $h$ of the shape $X$ in the base, and an embedding $e$ of this shape in $E$ above $h \, 0$ , we can construct a homotopy in $E$ whose projection is $h$ .

Cofibrations

In category theory, every construction has its dual, which is obtained by reversing all the arrows. In topology, there is an analogous relation called the Eckmann-Hilton duality. Besides reversing the arrows, it also dualizes products to exponentials (using the currying adjunction), and injections to surjections.

When dualizing the homotopy lifting diagram, we replace the trivial injection of $X \times \{0\} \cong X$ into $X \times I$ by a surjection $\varepsilon_0$ of the exponential $X^I$ onto $X$ . Here, $X^I$ is the set of functions $I \to X$ , or the path space of $X$ . The surjection $\varepsilon_0$ maps every path $\gamma \colon I \to X$ to its starting point by evaluating it at zero. (The evaluation map $\varepsilon_t \colon \gamma \mapsto \gamma \,t$ is continuous in the compact-open topology of $X^I$ .)

The homotopy lifting property is thus dualized to the homotopy extension property:

Corresponding to the fibration that deals with the failure of the injectivity of $p$ , the homotopy extension property deals with the failure of the surjectivity of $i$ .

If the mapping $i$ has the extension property for all topological spaces $X$ , it is called a cofibration.

Intuitively, a cofibration is an embedding of $B$ in $E$ such that any “spaghettification” of $B$ , that is embedding it in the path space $X^I$ , can be extended to a spaghettification of $E$ . $X$ plays the role of an ambient space where these operations can be visualized. Later we’ll see how to construct a minimal such ambient space called a mapping cylinder.

Let’s deconstruct the meaning of the outer commuting square.

$i$ embeds $B$ into $E$ .
$e$ further embeds $E$ into $X$ , and we end up with the embedding of $B$ inside $X$ given by $e \circ i$ .
$h$ embeds $B$ into the path space of $X$ (the dotted paths below).

The commuting condition for this square means that the starting points of all these paths, the result of applying $\varepsilon_0$ to each of them, coincide with the embedding of $B$ into $X$ given by $e \circ i$ . It’s like extruding a bunch of spaghetti, each strand corresponding to a point in $B$ .

With this setup, we postulate the existence of the diagonal mapping $\tilde h \colon E \to X^I$ that makes the two triangles commute. In other words, $E$ is mapped to a family of paths in $X$ which, when restricted to the image of $B$ coincide with the original mapping $h$ .

The spaghetti extruded through the $E$ shape contain the spaghetti extruded through the $B$ shape.

Another intuitive description of this situation uses the idea of homotopy as animation. The strands of spaghetti become trajectories of particles.

We start by setting up the initial scene. We embed $E$ in the big space $X$ using $e \colon E \to X$ .

We have the embedding $i \colon B \to E$ , which induces the embedding of $B$ into $X$ :

$b = e \circ i$

Then we animate the embedding of $B$ using the homotopy

$h \colon B \times I \to X$

The initial frame of this animation is given by $b$ :

$h(x, 0) = b \, x$

We say that $i$ is a cofibration if every such animation can be extended to the bigger animation:

$\tilde h \colon E \times I \to X$

whose starting frame is given by $e$ :

$\tilde h (x, 0) = e \, x$ .

The commuting condition (for the lower triangle) means that the two animations coincide for all $x \in B$ and $t \in I$ :

$h (x, t) = \tilde h (i \,x, t)$

Just like a fiber is an epitome of non-injectiveness, one can define a cofiber as an epitome of non-surjectiveness. It’s essentially the part of $E$ that is not covered by $i$ .

As a topological space it’s the result of shrinking the image of $B$ inside $E$ to a point (the resulting topology is called the quotient topology).

Notice that, unlike with fibers, there is just one cofiber for a given cofibration (up to homotopy equivalence).

Lifting Property

A category theorist looking at the two diagrams that define, respectively, homotopy lifting and extension, will immediately ignore all the superfluous details. She will turn the second diagram upside down and merge it with the first diagram to get:

This is how we read the new diagram: If for any morphisms $f$ and $g$ that make the outer square commute, there exist a diagonal morphism $h$ that makes the two triangles commute, then we say that $i$ has the left lifting property with respect to $p$ . Equivalently, $p$ has the right lifting property with respect to $i$ .

Or we can say that the two morphisms are orthogonal to each other.

The motivation for this nomenclature is interesting. In the category of sets, the archetypal non-surjective function is the “absurd” $0 \to 1$ (or, in set notation, $\emptyset \to \{*\}$ ). It turns out that all surjective functions are its right liftings. In other words, all surjections are right-orthogonal to the simplest non-surjective function.

Indeed, the function at the bottom $y \colon 1 \to Y$ picks an element $y \in Y$ . Similarly, the diagonal function picks an element $x \in X$ . The commuting triangle tells us that for every $y$ there exists an $x$ such that $y = p \, x$ .

Similarly, we can show that all injective functions are orthogonal to the archetypal non-injective function $2 \to 1$ (or $\{x_1, x_2\} \to \{*\}$ ).

Indeed, assume that $i$ maps two different elements $a_1, a_2 \in A$ to a single element $b \in B$ . We could then pick $f$ such that $f \, a_1 = x_1$ and $f \, a_2 = x_2$ . The diagonal $h$ can map $b$ to either $x1$ or $x2$ but not both, so we couldn’t make the upper triangle commute.

Incidentally, injections are also right-orthogonal to the archetypal non-injection.

Next: (Weak) Homotopy Equivalences.

July 25, 2016

Profunctors as Relations

Posted by Bartosz Milewski under Category Theory, Haskell, Homotopy Type Theory, Programming
[3] Comments

A profunctor is a categorical construct that takes relations to a new level. It is an embodiment of a proof-relevant relation.

We don’t talk enough about relations. We talk about domesticated relations — functions; or captive ones — equalities; but we don’t talk enough about relations in the wild. And, as is often the case in category theory, a less constrained construct may have more interesting properties and may lead to better insights.

Relations

A relation between two sets is defined as a set of pairs. The first element of each pair is from the first set, and the second from the second. In other words, it’s a subset of the cartesian product of two sets.

This definition may be extended to categories. If C and D are small categories, we can define a relation between objects as a set of pairs of objects. In general, such pairs are themselves objects in the product category C×D. We could define a relation between categories as a subcategory of C×D. This works as long as we ignore morphisms or, equivalently, work with discrete categories.

There is another way of defining relations using a characteristic function. You can define a function on the cartesian product of two sets — a function that assigns zero (or false) to those pairs that are not in a relation, and one (or true) to those which are.

Extending this to categories, we would use a functor rather than a function. We could, for instance, define a relation as a functor from C×D to Set — a functor that maps pairs of objects to either an empty set or a singleton set. The (somewhat arbitrary) choice of Set as the target category will make sense later, when we make connection between relations and hom-sets.

But a functor is not just a mapping of objects — it must map morphisms as well. Here, since we are dealing with a product category, our characteristic functor must map pairs of morphisms to functions between sets. We only worry about the empty set and the singleton set, so there aren’t that many functions to chose from.

The next question is: Should we map the two morphisms in a pair covariantly, or maybe map one of them contravariantly? To see which possibility makes more sense, let’s consider the case when D is the same as C. In other words, let’s look at relations between objects of the same category. There are actually categories that are based on relations, for instance preorders. In a preorder, two objects are in a relation if there is a morphism between them; and there can be at most one morphism between any two objects. A hom-set in a preorder can only be an empty set or a singleton set. Empty set — no relation. Singleton set — the objects are related.

But that’s exactly how we defined a relation in the first place — a mapping from a pair of objects to Set (how’s that for foresight). In a preorder setting, this mapping is nothing but the hom-functor itself. And we know that hom-functors are contravariant in the first argument and covariant in the second:

C(-,=) :: C^op×C -> Set

That’s an argument in favor of choosing mixed variance for the characteristic functor defining a relation.

A preorder is also called a thin category — a category where there’s at most one morphism per hom-set. Therefore a hom-functor in any thin category defines a relation.

Let’s dig a little deeper into why contravariance in the first argument makes sense in defining a relation. Suppose two objects a and b are related, i.e., the characteristic functor R maps the pair <a, b> to a singleton set. In the hom-set interpretation, where R is the hom-functor C(-, =), it means that there is a single morphism r:

r :: a -> b

Now let’s pick a morphism in C^op×C that goes from <a, b> to some <s, t>. A morphism in C^op×C is a pair of morphisms in C:

f :: s -> a
g :: b -> t

The composition of morphisms g ∘ r ∘ f is a morphism from s to t. That means the hom-set C(s, t) is not empty — therefore s and t are related.

And they should be related. That’s because the functor R acting on <f, g> must yield a function from the set C(a, b) to the set C(s, t). There’s no function from a non-empty set to the empty set. So, if the former is non-empty, the latter cannot be empty. In other words, if b is related to a and there is a morphism from <a, b> to <s, t> then t is related to s. We were able to “transport” the relation along a morphism. By making the characteristic functor R contravariant in the first argument and covariant in the second, we automatically make the relation compatible with the structure of the category.

In general, hom-sets are not constrained to empty and singleton sets. In an arbitrary category C, we can still think of hom-sets as defining some kind of generalized relation between objects. The empty hom-set still means no relation. Non-empty hom-sets can be seen as multiple “proofs” or “witnesses” to the relation.

Now that we know that we can imitate relations using hom-sets, let’s take a step back. I can think of two reasons why we would like to separate relations from hom-sets: One is that relations defined by hom-sets are always reflexive because of identity morphisms. The other reason is that we might want to define various relations on top of an existing category, a category that has its own hom-sets. It turns out that a profunctor is just the answer.

Profunctors

A profunctor assigns sets to pairs of objects — possibly objects taken from two different categories — and it does it in a way that’s compatible with the structure of these categories. In particular, it’s a functor that’s contravariant in its first argument and covariant in the second:

C^op × D -> Set

Interpreting elements of such sets as individual “proofs” of a relation, makes a profunctor a kind of proof-relevant relation. (This is very much in the spirit of Homotopy Type Theory (HoTT), where one considers proof-relevant equalities.)

In Haskell, we substitute all three categories in the definition of the profunctor with the category of types and functions; which is essentially Set, if you ignore the bottom values. So a profunctor is a functor from Set^op×Set to Set. It’s a mapping of types — a two-argument type constructor p, and a mapping of morphisms. A morphism in Set^op×Set is a pair of functions going between pairs of sets (a, b) and (s, t). Because of contravariance, the first function goes in the opposite direction:

(s -> a, b -> t)

A profunctor lifts this pair to a single function:

p a b -> p s t

The lifting is done by the function dimap, which is usually written in the curried form:

class Profunctor p where
    dimap :: (s -> a) -> (b -> t) -> p a b -> p s t

Profunctor Composition

As with any construction in category theory, we would like to know if profunctors are composable. But how do you compose something that has two inputs that are objects in different categories and one output that is a set? Just like with a Tetris block, we have to turn it on its side. Profunctors generalize relations between categories, so let’s compose them like relations.

Suppose we have a relation P from C to X and another relation Q from X to D. How do we build a composite relation between C and D? The standard way is to find an object in X that can serve as a bridge. We need an object x that is in a relation P with c (we’ll write it as c P x), and with which d in a relation Q (denoted as x Q d). If such an object exists, we say that d is in a relation with c — the relation being the composition of P and Q.

We’ll base the composition of profunctors on the same idea. Except that a profunctor produces a whole set of proofs of a relation. We not only have to provide an x that is related to both c and d, but also compose the proofs of these relations.

By convention, a profunctor from x to c, p x c, is interpreted as a relation from c to x (what we denoted c P x). So the first step in the composition is finding an x such that p x c is a non-empty set and for which q d x is also a non-empty set. This not only establishes the two relations, but also generates their proofs — elements of sets. The proof that both relations are in force is simply a pair of proofs (a logical conjunction, in terms of propositions as types). The set of such pairs, or the cartesian product of p x c and q d x, for some x, defines the composition of profunctors.

Have a look at this Haskell definition (in Data.Profunctor.Composition):

data Procompose p q d c where
  Procompose :: p x c -> q d x -> Procompose p q d c

Here, the cartesian product (p x c, q d x) is curried, and the existential quantifier over x is implicit in the use of the GADT.

This Haskell definition is a special case of a more general definition of the composition of profunctors that relate arbitrary categories. The existential quantifier in this case is represented by a coend:

(p ∘ q) d c = ∫^x (p x c) × (q d x)

Since profunctors can be composed, it’s natural to ask if they form a category. It turns out that, rather than being a traditional category (it’s not, because profunctor composition is associative and unital only up to an isomorphism), they form a bicategory called Prof. The objects in that category are categories, morphisms are profunctors, and the role of the identity morphism is played by the hom-functor C(-,=) — our prototypical profunctor.

The fact that the hom-functor is the unit of profunctor composition follows from the so-called ninja Yoneda lemma. This can be also explained in terms of relations. The hom-functor establishes a relation between any two objects that are connected by at least one morphism. As I mentioned before, this relation is reflexive. It follows that if we have a “proof” of p d c, we can immediately compose it with the trivial “proof” of C(d, d), which is id_d and get the proof of the composition

(p ∘ C(-, =)) d c

Conversely, if this composition exists, it means that there is a non-empty hom-set C(d, x) and a proof of p x c. We can then take the element of C(d, x):

f :: d -> x

pair it with an identity at c, and lift the pair:

<f, id_c>

using p to transform p x c to p d c — the proof that d is in relation with c. The fact that the relation defined by a profunctor is compatible with the structure of the category (it can be “transported” using a morphism in the product category C^op×D) is crucial for this proof.

Acknowledgments

I’m grateful to Gershom Bazerman for useful comments and to André van Meulebrouck for checking the grammar and spelling.

July 29, 2013

Quantum Homotopy Computer

Posted by Bartosz Milewski under Homotopy Type Theory, Programming, Type System | Tags: foundations of mathematics, type theories |
[9] Comments

This is my 100th WordPress post, so I decided to pull all the stops and go into some crazy stuff where hard math and hard physics mix freely with wild speculation. I hope you will enjoy reading it as much as I enjoyed writing it.

It’s a HoTT Summer of 2013

One of my current activities is reading the new book, Homotopy Type Theory (HoTT) that promises to revolutionize the foundations of mathematics in a way that’s close to the heart of a programmer. It talks about types in the familiar sense: Booleans, natural numbers, (polymorphic) function types, tuples, discriminated unions, etc.

As do previous type theories, HoTT assumes the Curry-Howard isomorphism that establishes the correspondence between logic and type theory. The gist of it is that any theorem can be translated into a definition of a type; and its proof is equivalent to producing a value of that type (false theorems correspond to uninhabited types that have no elements). Such proofs are by necessity constructive: you actually have to construct a value to prove a theorem. None if this “if it didn’t exist then it would lead to contradictions” negativity that is shunned by intuitionistic logicians. (HoTT doesn’t constrain itself to intuitionistic logic — too many important theorems of mathematics rely on non-constructive proofs of existence — but it clearly delineates its non-intuitionistic parts.)

Type theory has been around for some time, and several languages and theorem provers have been implemented on the base of the Curry-Howard isomorphism: Agda and Coq being common examples. So what’s new?

Set Theory Rant

Here’s the problem: Traditional type theory is based on set theory. A type is defined as a set of values. Bool is a two-element set {True, False}. Char is a set of all (Unicode) characters. String is an infinite set of all lists of characters. And so on. In fact all of traditional mathematics is based on set theory. It’s the “assembly language” of mathematics. And it’s not a very good assembly language.

First of all, the naive formulation of set theory suffers from paradoxes. One such paradox, called Russell’s paradox, is about sets that are members of themselves. A “normal” set is not a member of itself: a set of dogs is not a dog. But a set of all non-dogs is a member of itself — it’s “abnormal”. The question is: Is the set of all “normal” sets normal or abnormal? If it’s normal that it’s a member of normal sets, right? Oops! That would make it abnormal. So maybe it’s abnormal, that is not a member of normal sets. Oops! That would make it normal. That just shows you that our natural intuitions about sets can lead us astray.

Fortunately there is an axiomatic set theory called the Zermelo–Fraenkel (or ZF) theory, which avoids such paradoxes. There are actually two versions of this theory: with or without the Axiom of Choice. The version without it seems to be too weak (not every vector space has a basis, the product of compact sets isn’t necessarily compact, etc.); the one with it (called ZFC) leads to weird non-intuitive consequences.

What bothers many mathematicians is that proofs that are based on set theory are rarely formal enough. It’s not that they can’t be made formal, it’s just that formalizing them would be so tedious that nobody wants to do it. Also, when you base any theory on set theory, you can formulate lots of idiotic theorems that have nothing to do with the theory in question but are only relevant to its clunky set-theoretical plumbing. It’s like the assembly language leaking out from higher abstractions. Sort of like programming in C.

Donuts are Tastier than Sets

Tired of all this nonsense with set theory, a group of Princeton guys and their guests decided to forget about sets and start from scratch. Their choice for the foundation of mathematics was the theory of homotopy. Homotopy is about paths — continuous maps from real numbers between 0 and 1 to topological spaces; and continuous deformations of such paths. The properties of paths capture the essential topological properties of spaces. For instance, if there is no path between a and b, it means that the space is not connected — it has at least two disjoint components — a sits in one and b in another.

Two paths from a to b that cannot be continuously deformed into each other

If two paths between a and b cannot be deformed into each other, it means that there is a hole in space between them.

Obviously, this “traditional” formulation of homotopy relies heavily on set theory. A topological space, for instance, is defined in terms of open sets. So the first step is to distill the essence of homotopy theory by getting rid of sets. Enter Homotopy Type Theory. Paths and their deformations become primitives in the theory. We still get to use our intuitions about paths as curves inscribed on surfaces, but otherwise the math is totally abstract. There is a small set of axioms, the basic one asserting that the statement that a and b are equivalent is equivalent to the statement that they are equal. Of course the notions of equivalence and equality have special meanings and are very well defined in terms of primitives.

Cultural Digression

Why homotopy? I have my own theory about it. Our mathematics has roots in Ancient Greece, and the Greeks were not interested in developing technology because they had very cheap labor — slaves.

Euclid explaining geometry to his pupils in Raphael’s School of Athens

Instead, like all agricultural societies before them (Mesopotamia, Egypt), they were into owning land. Land owners are interested in geometry — Greek word γεωμετρία literally means measuring Earth. The “computers” of geometry were the slate, ruler and compass. Unlike technology, the science of measuring plots of land was generously subsidized by feudal societies. This is why the first rigorous mathematical theory was Euclid’s geometry, which happened to be based on axioms and logic. Euclid’s methodology culminated in the 20th century in Hilbert’s program of axiomatization of the whole of mathematics. This program crashed and burned when Gödel proved that any non-trivial theory (one containing arithmetic) is chock full of non-decidable theorems.

I was always wondering what mathematics would be like if it were invented by an industrial, rather than agricultural, society. The “computer” of an industrial society is the slide rule, which uses (the approximation of) real numbers and logarithms. What if Newton and Leibniz never studied Euclid? Would mathematics be based on calculus rather than geometry? Calculus is not easy to axiomatize, so we’d have to wait for the Euclid of calculus for a long time. The basic notions of calculus are Banach spaces, topology, and continuity. Topology and continuity happen to form the basis of homotopy theory as well. So if Greeks were an industrial society they could have treated homotopy as more basic than geometry. Geometry would then be discovered not by dividing plots of land but by studying solutions to analytic equations. Instead of defining a circle as a set of points equidistant from the center, as Euclid did, we would first define it as a solution to the equation x²+y²=r².

Now imagine that this hypothetical industrial society also skipped the hunter-gather phase of development. That’s the period that gave birth to counting and natural numbers. I know it’s a stretch of imagination worthy a nerdy science fiction novel, but think of a society that would evolve from industrial robots if they were abandoned by humanity in a distant star system. Such a society could discover natural numbers by studying the topology of manifolds that are solutions to n-dimensional equations. The number of holes in a manifold is always a natural number. You can’t have half a hole!

Instead of counting apples (or metal bolts) they would consider the homotopy of the two-apple space: Not all points in that space can be connected by continuous paths.

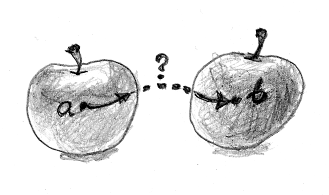
There is no continuous path between a and b

Maybe in the world where homotopy were the basis of all mathematics, Andrew Wiles’s proof of the Fermat’s Last Theorem could fit in a margin of a book — as long as it were a book on cohomology and elliptic curves (some of the areas of mathematics Wiles used in his proof). Prime numbers would probably be discovered by studying the zeros of the Riemann zeta function.

Industrial robot explaining to its pupils the homotopy of a two-apple space.

Quantum Digression

If our industrial robots were very tiny and explored the world at the quantum level (nanorobots?), they might try counting particles instead of apples. But in quantum mechanics, a two-particle state is not a direct product of two one-particle states. Two particles share the same wave function. In some cases this function can be factorized when particles are far apart, in others it can’t, giving rise to quantum entanglement. In quantum world, 2 is not always equal to 1+1.

In Quantum Field Theory (QFT — the relativistic counterpart of Quantum Mechanics), physicist calculate the so called S matrix that describes idealized experiments in which particles are far away from each other in the initial and final states. Since they don’t interact, they can be approximated by single-particle states. For instance, you can start with a proton and an antiproton coming at each other from opposite directions. They can be approximated as two separate particles. Then they smash into each other, produce a large multi-particle mess that escapes from the interaction region and is eventually seen as (approximately) separate particles by a big underground detector. (That’s, for instance, how the Higgs boson was discovered.) The number of particles in the final state may very well be different from the number of particles in the initial state. In general, QFT does not preserve the number of particles. There is no such conservation law.

Counting particles is very different from counting apples.

Relaxing Equality

In traditional mathematics, the notions of isomorphism and equality are very different. Isomorphism means (in Greek, literally) that things have the same shape, but aren’t necessarily equal. And yet mathematicians often treat isomorphic things as if they were equal. They prove a property of one thing and then assume that this property is also true for all things isomorphic. And it usually is, but nobody has the patience to prove it on the case-by-case basis. This phenomenon even has its own name: abuse of notation. It’s like writing programs in a language in which equality ‘==’ does not translate into the assembly-language CMP instruction followed be a conditional jump. We would like to work with structural identity, but all we do is compare pointers. You can overload operator ‘==’ in C++ but many a bug was the result of comparing pointers instead of values.

How can we make isomorphism more like equality? HoTT took quite an unusual approach by relaxing equality enough to make it plausibly equivalent to isomorphism.

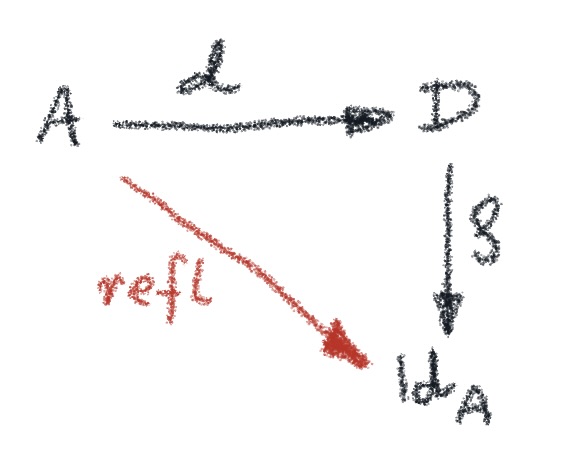
HoTT’s homotopic version of equality is this: Two things are equal if there is a path between them. This equality is reflexive, symmetric, and transitive, just like equality is supposed to be. Reflexivity, for instance, tells us that x=x, and indeed there is always a trivial (constant) path from a point to itself. But there could also be other non-trivial paths looping from the point to itself. Some of them might not even be contractible. They all contribute to equality x=x.

There could be several paths between different points, a and b, making them “equal”: a=b. We are tempted to say that in this picture equality is a set of paths between points. Well, not exactly a set but the next best thing to a set — a type. So equality is a type, often called “identity type”, and two things are equal if the “identity type” for them is inhabited. That’s a very peculiar way to define equality. It’s an equality that carries with it a witness — a construction of an element of the equality type.

Relaxing Isomorphism

The first thing we could justifiably expect from any definition of equality is that if two things are equal they should be isomorphic. In other words, there should be an invertible function that maps one equal thing to another equal thing. This sound pretty obvious until you realize that, since equality is relaxed, it’s not! In fact we can’t prove strict isomorphism between things that are homotopically equal. But we do get a slightly relaxed version of isomorphism called equivalence. In HoTT, if things are equal they are equivalent. Phew, that’s a relief!

The trick is going the other way: Are equivalent things equal? In traditional mathematics that would be blatantly wrong — there are many isomorphic objects that are not equal. But with the HoTT’s notion of equality, there is nothing that would contradict it. In fact, the statement that equivalence is equivalent to equality can be added to HoTT as an axiom. It’s called Voevodski’s axiom of univalence.

It’s hard (or at least tedious), in traditional math, to prove that properties (propositions) can be carried over isomorphisms. With univalence, equivalence (generalized isomorphism) is the same as equality, and one can prove once and for all that propositions can be transported between equal objects. With univalence, the tedium of proving that if one object has a given property then all equivalent (“isomorphic”) object have the same property is eliminated.

Incidentally, where do types live? Is there (ahem!) a set of all types? There’s something better! A type of types called a Universe. Since a Universe is a type, is it a member of itself? You can almost see the Russel’s paradox looming in the background. But don’t despair, a Universe is not a member of itself, it’s a member of the higher Universe. In fact there are infinitely many Universes, each being a member of the next one.

Taking Roots

How does relaxed equality differ from the set-theoretical one? The simplest such example is the equality of Boolean types. There are two ways you can equal the Bool type to itself: One maps True to True and False to False, the other maps True to False and False to True. The first one is an identity mapping, but the second one is not — its square though is! (apply this mapping twice and you get back to original). Within HoTT you can take the square root of identity!

So here’s an interesting intuition for you: HoTT is to set theory as complex numbers are to real numbers (in complex numbers you can take a square root of -1). Paradoxically, complex numbers make a lot of things simpler. For instance, all quadratic equations are suddenly solvable. Sine and cosine become two projections of the same complex exponential. Riemann’s zeta function gains very interesting zeros on the imaginary line. The hope is that switching from sets to homotopy will lead to similar simplifications.

I like the example with flipping Booleans because it reminds me of an interesting quantum phenomenon. Imagine a quantum state with two identical particles. What happens when you switch the particles? If you get exactly the same state, the particles are called bosons (think photons). If you don’t, they are called fermions (think electrons). But when you flip fermions twice, you get back to the original state. In many ways fermions behave like square roots of bosons. For instance their equation of motion (Dirac equation) when squared produces the bosonic equation of motion (Klein-Gordon equation).

Computers Hate Sets

There is another way HoTT is better than set theory. (And, in my cultural analogy, that becomes more pertinent when an industrial society transitions to a computer society.) There is no good way to represent sets on a computer. Data structures that model sets are all fake. They always put some restrictions on the type of elements they can store. For instance the elements must be comparable, or hashable, or something. Even the simplest set of just two elements is implemented as an ordered pair — in sets you can’t have the first or the second element of a set (and in fact the definition of a pair as a set is quite tricky). You can easily write a program in Haskell that would take a (potenitally infinite) list of pairs and pick one element from each pair to form a (potentially infinite) list of picks. You can, for instance, tell the computer to pick the left element from each pair. Replace lists of pairs with sets of sets and you can’t do it! There is no constructive way of creating such a set and it’s very existence hinges on the axiom of choice.

This fact alone convinces me that set theory is not the best foundation for the theory of computing. But is homotopy a better assembly language for computing? We can’t represent sets using digital computers, but can we represent homotopy? Or should we start building computers from donuts and rubber strings? Maybe if we keep miniaturizing our computers down to the Planck scale, we could find a way to do calculations using loop quantum gravity, if it ever pans out.

Aharonov-Bohm Experiment

Even without invoking quantum gravity, quantum mechanics exhibits a lot of interesting non-local behaviors that often probe the topological properties of the surroundings. For instance, in the classic double-slit experiment, the fact that there are paths between the source of electrons and the screen that are not homotopically equivalent makes the electrons produce an interference pattern. But my favorite example is the Bohm-Aharonov experiment.

First, let me explain what a magnetic potential is. One of the Maxwell’s equations states that the divergence of the magnetic field is always zero (see a Tidbit at the end of this post that explains this notation):

This is the reason why magnetic field lines are always continuous. Interestingly, this equation has a solution that follows from the observation that the divergence of a curl is zero. So we can represent the magnetic field as a curl of some other vector field, which is called the magnetic potential A:

It’s just a clever mathematical trick. There is no way to measure magnetic potential, and the solution isn’t even unique: you can add a gradient of any scalar field to it and you’ll get the same magnetic field (the curl of a gradient is zero). So A is totally fake, it exists only as a device to simplify some calculations. Or is it…?

It turns out that electrons can sniff the magnetic potential, but only if there’s a hole in space. It turns out that, if you have a thin (almost) infinite linear coil with a current running through its windings, (almost) all magnetic field will be confined to its interior. Outside the coil there’s no magnetic field. However, there is a nonzero curl-free magnetic potential circling it. Now imagine using this coil as a separator between the two slits of the double-slit experiment. As before, there are two paths for the electron to follow: to the left of the coil and to the right of the coil. But now, along one path, the electron will be traveling with the lines of magnetic potential; along the other, against.

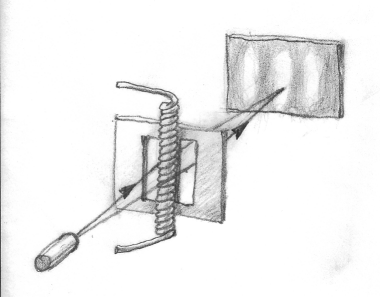
Aharononv-Bohm experiment. There are two paths available to the electron.

Magnetic potential doesn’t contribute to the electron’s energy or momentum but it does change its phase. So in the presence of the coil, the interference pattern in the two slit experiment shifts. That shift has been experimentally confirmed. The Aharonov-Bohm effect takes place because the electron is excluded from the part of space that is taken up by the coil — think of it as an infinite vertical line in space. The space available to the electron contains paths that cannot be continuously deformed into each other (they would have to cross the coil). In HoTT that would mean that although the point a, which is the source of the electron, and point b, where the electron hit the screen, are “equal,” there are two different members of the equality type.

The Incredible Quantum Homotopy Computer

The Aharonov-Bohm effect can be turned on and off by switching the current in the coil (actually, nobody uses coils in this experiment, but there is some promising research that uses nano-rings instead). If you can imagine a transistor built on the Aharonov-Bohm principle, you can easily imagine a computer. But can we go beyond digital computers and really explore varying homotopies?

I’ll be the first to admit that it might be too early to go to Kickstarter and solicit funds for a computer based on the Aharonov-Bohm effect that would be able to prove theorems formulated using Homotopy Type Theory; but the idea of breaking away from digital computing is worth a thought or two.

Or we can leave it to the post apocalyptic industrial-robot civilization that doesn’t even know what a digit is.

Acknowledgments

I’m grateful to the friendly (and patient) folks on the HoTT IRC channel for answering my questions and providing valuable insights.

Tidbit about Differential Operators

What are all those curls, divergences, and gradients? It’s just some vectors in 3-D space.

A scalar field φ(x, y, z) is a single function of space coordinates x, y, and z. You can calculate three different derivatives of this function with respect to x, y, and z. You can symbolically combine these three derivatives into one vector, (∂_x, ∂_y, ∂_z). There is a symbol for that vector, called a nabla: ∇. If you apply a nabla to a scalar field, you get a vector field that is called the gradient, ∇φ, of that field. In coordinates, it is: (∂_xφ, ∂_yφ, ∂_zφ).

A vector field V(x, y, z) is a triple of functions forming a vector at each point of space, (V_x, V_y, V_z). Magnetic field B and magnetic potential A are such vector fields. There are two ways you can apply a nabla to a vector field. One is just a scalar product of the nabla and the vector field, ∇·V, and it’s called the divergence of the vector field. In components, you can rewrite it as ∂_xV_x + ∂_yV_y + ∂_zV_z.

The other way of multiplying two vectors is called the vector product and its result is a vector. The vector product of the nabla and a vector field, ∇×A, is called the curl of that field. In components it is: (∂_yA_z – ∂_zA_y, ∂_zA_x – ∂_xA_z, ∂_xA_y – ∂_yA_x).

The vector product of two vectors is perpendicular to both. So when you then take a scalar product of the vector product with any of the original vectors, you get zero. This works also with nablas so, for instance, ∇·(∇×A) = 0 — the divergence of a curl is zero. That’s why the solution to ∇·B is B = ∇×A.

Similarly, because the vector product of a vector with itself is zero, we get ∇×∇φ = 0 — the curl of a gradient is zero. That’s why we can always add a term of the form ∇φ to A and get the same field B. In physics, this freedom is called gauge invariance.

Bartosz Milewski's Programming Cafe