Previously: Subobject Classifier.

In category theory, objects are devoid of internal structure. We’ve seen however that in certain categories we can define relationships between objects that mimic the set-theoretic idea of one set being the subset of another. We do this using the subobject classifier.

We would like to define a subobject classifier in the category of presheaves, so we could easily characterize subfunctors of a given presheaf. This will help us work with sieves, which are subfunctors of the hom-functor C(-, a); and coverages, which are special kinds of sieves.

Recall that a presheaf S is a subfunctor of another presheaf P \colon C^{op} \to Set if it satisfies two conditions.

  • For every object a, we have a set inclusion: S a \subseteq P a,
  • For every morphism f \colon c \to a, the function S f \colon S a \to S c is a restriction of the function P f \colon P a \to P c. In other words, P f and S f must agree on the subset S a.

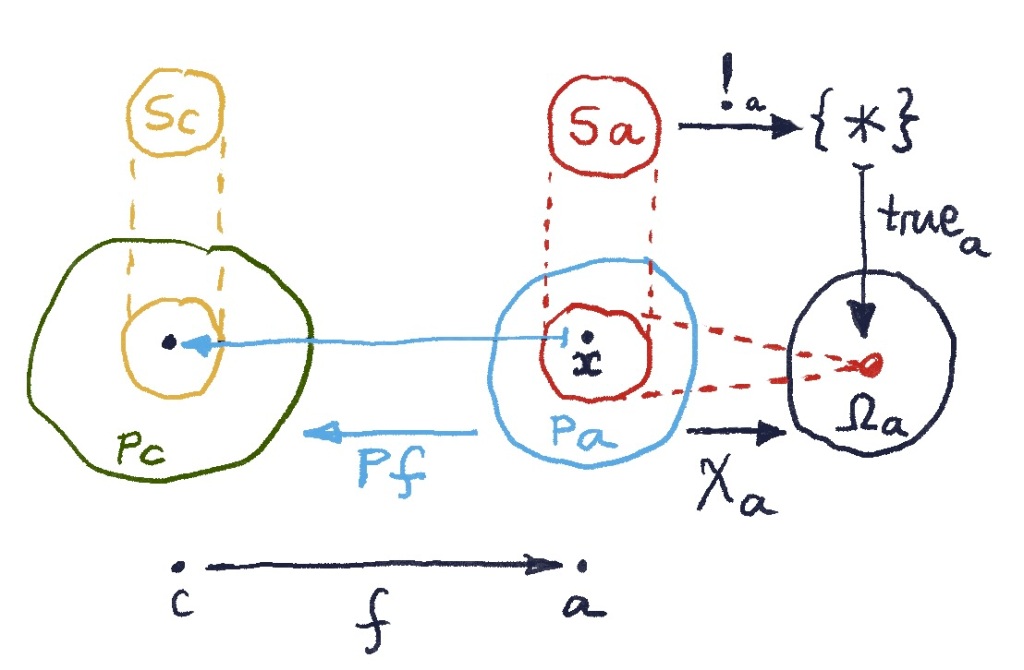
As category theory goes, this is a very low-level definition. We need something more abstract: We need to construct a subobject classifier in the category of presheaves. Recall that a subobject classifier is defined by the following pullback diagram:

This time, however, the objects are presheaves and the arrows are natural transformations.

To begin with we have to define a terminal presheaf, 1 \colon C^{op} \to Set that satisfies the condition that, for any presheaf P, there is a unique natural transformation ! \colon P \to 1. This will work if every component !_a \colon P a \to 1 a of this natural transformation is unique, which is true if we choose 1 a to be the terminal singleton set \{ * \}. Thus the terminal presheaf maps all objects to the terminal set, and all morphisms to the identity on \{ * \}.

Next, let’s instantiate the subobject classifier diagram at a particular object a.

Here, the component true_a picks a special “True” element in the set \Omega_a. If the presheaf S is a subfunctor of P, the set S a is a subset of P a. The function \chi_a must therefore map the whole subset S a to “True”. This is consistent with our definition of the subobject classifier for sets.

The second condition in the definition of a subfunctor is more interesting. It involves the mapping of morphisms.

The restriction condition

We have to consider all morphisms converging on our object of interest a. For instance, lets take f \colon c \to a. The presheaf P lifts it to a function P f \colon P a \to P c. If S is a subfunctor of P, S f is a restriction of P f.

Specifically the restriction condition tells us that, if we pick an element x \in S a, then both P f and S f will map it to the same element of S c. In fact, when defining a subobject, we only care if the embedding of S c in P c is injective (monomorphic). It’s okay if it permutes the elements of S c. So it’s enough that, for all x \in S a, the following condition is satisfied:

(P f) x \in S c

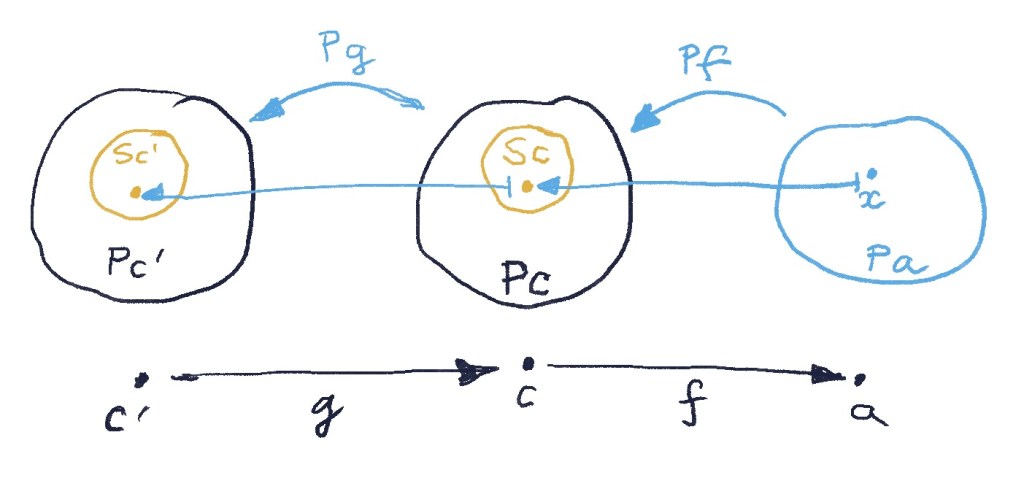
Now consider an arbitrary x \in P a (not necessarily an element of S a). We can gather all arrows f converging on a for which the subset-mapping condition is satisfied:

(P f) x \in S c

If S is a subfunctor of P, these arrows form a sieve on a, as any composition f \circ g also satisfies the subset-mapping condition:

Moreover, if x is in fact an element of S a, this sieve is the maximal sieve. A maximal sieve on a is a collection of all arrows converging on a.

We can now define a function \chi_a that assigns to each x \in P a the sieve of arrows that satisfy the subset-mapping condition.

\chi_a x = \{f \colon c \to a \, | \, (P f) x \in S c\}

The function \chi_a has the property that, if x is an element of S a, the result is the maximal sieve on a.

It makes sense then to define \Omega_a as a set of sieves on a, and “True” as the maximal sieve on a. (Thus \Omega_a is a set whose elements are sets.)

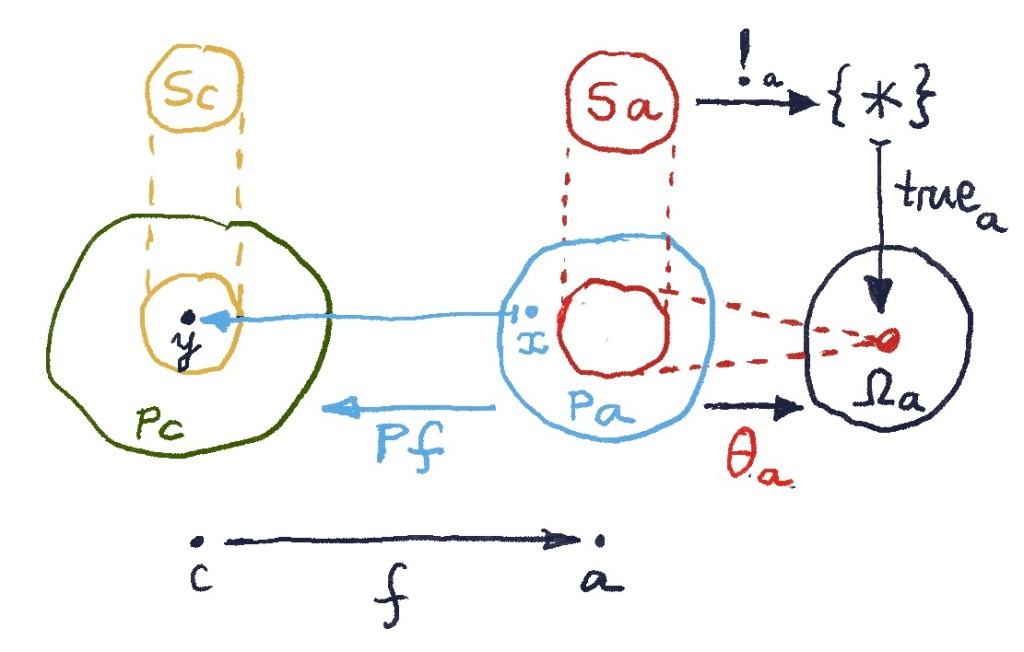
The mapping \Omega \colon a \to \Omega_a can be made into a presheaf by defining its action on morphisms. The lifting of f \colon c \to a takes a sieve s_a \in \Omega_a to a sieve s'_{c} \in \Omega c, defined as a set of arrows h \colon c' \to c, such that f \circ h \in s_a.

Notice that the resulting sieve s_c' is maximal if and only if f \in \Omega_a. (Hint: If a sieve is maximal, then it contains identity.)

It can be shown that the the functions \chi_a combine to form a natural transformation \chi \colon P \to \Omega.

What remains to be shown is that this \chi is a unique such natural transformation that completes the pullback:

To show that, let’s assume that there is another natural transformation \theta \colon P \to \Omega making this diagram into a pullback. Let’s redraw the subfunctor condition for arrows, replacing \chi with \theta:

Let’s pick an x \in P a and call y = (P f) x. We’ll follow a set of equivalences.

The pullback condition:

tells us that y \in S c is equivalent to \theta_c y = true_c. In other words:

\theta_c ((P f) x) = true_c

Using naturality of \theta:

we can rewrite it as:

(\Omega f) (\theta_a x) = true_c.

Both sides of this equation are sieves. By definition, the lifting of f, \Omega f, acting on \theta_a x is a sieve defined by the following set of arrows:

(\Omega f) (\theta_a x) = \{ h \colon c' \to c \, | \, f \circ h \in \theta_a x \}

Since true_c is a maximal sieve, it must be that f \in \theta_a x.

We have shown that the condition (P f) x \in S c is equivalent to f \in \theta_a x. But the first condition is exactly the one we used to define \chi_a x. Therefore \chi is the only function that makes the subobject classifier diagram into a pullback.

Subfunctor classifier

The subobject classifier in the category of presheaves is thus a presheaf \Omega that maps objects to sieves, together with the natural transformation true \colon 1 \to \Omega that picks maximal sieves.

Every natural transformation \chi \colon P \to \Omega defines a subfunctor of the presheaf P. The components of this natural transformation serve as characteristic functions for the sets P a. A given element x is in the subset S a iff \chi_a maps it to the maximal sieve on a.

But there’s not one but many different ways of failing the subset test. They are given by non-maximal sieves. We may think of them as satisfying the Anna Karenina principle, “All happy families are alike; each unhappy family is unhappy in its own way.”

Why sieves? Because once an element of a set P a is mapped by P f to an element of a subset S c, it will continue to be mapped into consecutive subsets S c', etc. The network of “happy” morphisms keeps growing outward. By contrast, the “unhappy” elements of x \in P a have at least one morphism f \colon c \to a, whose lifting maps it outside the subset S c. That’s the morphism that’s absent from the non-maximal sieve \chi_a. Finally, naturality of \chi ensures that subset conditions propagate coherently from object to object.

Next: Fibrations and Cofibrations.