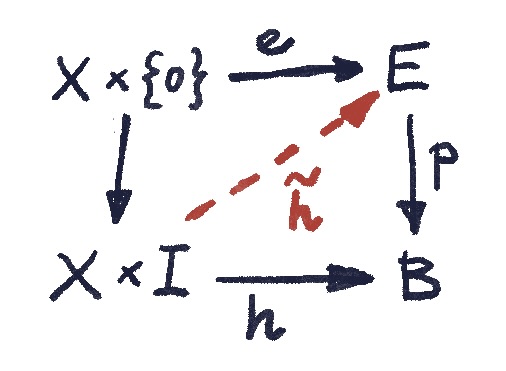Fibration | Bartosz Milewski's Programming Cafe

Previously: Subfunctor Classifier.

We are used to thinking of a mapping as either being invertible or not. It’s a yes or no question. A mapping between sets is invertible if it’s both injective and surjective. It means that it never merges two elements into one, and it covers the whole target set.

But if you are willing to look closer, the failures of invertibility are a whole fascinating area of research. Things get a lot more interesting if you consider mapping between topological spaces, which have to skillfully navigate around various holes and tears in the target space, and shrink or glue together parts of the source space. I will be glossing over some of the topological considerations, concentrating on the big-picture intuitions (both culinary and cinematographic).

Fibrations

In what follows, we’ll be considering a function $p \colon E \to B$ . We’ll call $p$ a projection from the total set $E$ to the base set $B$ .

Let’s start by considering the first reason for a failure of invertibility: multiple elements being mapped into one. Even though we can’t invert such a mapping, we can use it to fibrate the source $E$ .

To each element $y \in B$ we’ll assign a fiber, the set of elements of $E$ that are mapped to $y$ . By abuse of notation, we call such a fiber $p^{-1} y$ :

$p^{-1} y = \{ x |\; p x = y \}$

For some $y$ ‘s, this set may be empty $\emptyset$ ; for others, it may contain lots elements.

Notice that $p$ is an isomorphism if and only if every fiber is a singleton set. This property gives rise to a very useful definition of equivalence in homotopy type theory, where we ask for every fiber to be contractible.

A set-theoretic union of all fibers reconstructs the total set $E$ .

Things get more interesting when we move to topological spaces and continuous functions. To begin with, we can define a path in $B$ as a continuous mapping from the unit interval $I = [0, 1]$ to $B$ .

$\gamma \colon I \to B$

We can then ask if it’s possible to lift this path to $E$ , that is to construct $\tilde{\gamma} \colon I \to E$ that lies above $\gamma$ . To do this, we pick the starting point $e \in E$ that lies above the starting point of $\gamma$ , that is $p \,e = \gamma \,0$ .

This setup can be summarized in the commuting square:

The lifting $\tilde{\gamma}$ is then the diagonal arrow that makes both triangles commute:

It’s helpful to imagine a path as a trajectory of a point moving through a topological space. The parameter $t \in I$ is then interpreted as time.

In homotopy theory we generalize this idea to the movement, or deformation, of arbitrary shapes, not just points.

If we describe such a shape as the image of some topological space $X$ , its deformation is a mapping $h \colon X \times I \to B$ . Such potentially “fat” paths are called homotopies. In particular, if we replace $X$ by a single point, we recover our “thin” paths.

A homotopy lifting property is expressed as the existence of the diagonal function $\tilde h$ in this commuting square, such that the resulting triangles commute:

In other words, given a homotopy $h$ of the shape $X$ in the base, and an embedding $e$ of this shape in $E$ above $h \, 0$ , we can construct a homotopy in $E$ whose projection is $h$ .

Cofibrations

In category theory, every construction has its dual, which is obtained by reversing all the arrows. In topology, there is an analogous relation called the Eckmann-Hilton duality. Besides reversing the arrows, it also dualizes products to exponentials (using the currying adjunction), and injections to surjections.

When dualizing the homotopy lifting diagram, we replace the trivial injection of $X \times \{0\} \cong X$ into $X \times I$ by a surjection $\varepsilon_0$ of the exponential $X^I$ onto $X$ . Here, $X^I$ is the set of functions $I \to X$ , or the path space of $X$ . The surjection $\varepsilon_0$ maps every path $\gamma \colon I \to X$ to its starting point by evaluating it at zero. (The evaluation map $\varepsilon_t \colon \gamma \mapsto \gamma \,t$ is continuous in the compact-open topology of $X^I$ .)

The homotopy lifting property is thus dualized to the homotopy extension property:

Corresponding to the fibration that deals with the failure of the injectivity of $p$ , the homotopy extension property deals with the failure of the surjectivity of $i$ .

If the mapping $i$ has the extension property for all topological spaces $X$ , it is called a cofibration.

Intuitively, a cofibration is an embedding of $B$ in $E$ such that any “spaghettification” of $B$ , that is embedding it in the path space $X^I$ , can be extended to a spaghettification of $E$ . $X$ plays the role of an ambient space where these operations can be visualized. Later we’ll see how to construct a minimal such ambient space called a mapping cylinder.

Let’s deconstruct the meaning of the outer commuting square.

$i$ embeds $B$ into $E$ .
$e$ further embeds $E$ into $X$ , and we end up with the embedding of $B$ inside $X$ given by $e \circ i$ .
$h$ embeds $B$ into the path space of $X$ (the dotted paths below).

The commuting condition for this square means that the starting points of all these paths, the result of applying $\varepsilon_0$ to each of them, coincide with the embedding of $B$ into $X$ given by $e \circ i$ . It’s like extruding a bunch of spaghetti, each strand corresponding to a point in $B$ .

With this setup, we postulate the existence of the diagonal mapping $\tilde h \colon E \to X^I$ that makes the two triangles commute. In other words, $E$ is mapped to a family of paths in $X$ which, when restricted to the image of $B$ coincide with the original mapping $h$ .

The spaghetti extruded through the $E$ shape contain the spaghetti extruded through the $B$ shape.

Another intuitive description of this situation uses the idea of homotopy as animation. The strands of spaghetti become trajectories of particles.

We start by setting up the initial scene. We embed $E$ in the big space $X$ using $e \colon E \to X$ .

We have the embedding $i \colon B \to E$ , which induces the embedding of $B$ into $X$ :

$b = e \circ i$

Then we animate the embedding of $B$ using the homotopy

$h \colon B \times I \to X$

The initial frame of this animation is given by $b$ :

$h(x, 0) = b \, x$

We say that $i$ is a cofibration if every such animation can be extended to the bigger animation:

$\tilde h \colon E \times I \to X$

whose starting frame is given by $e$ :

$\tilde h (x, 0) = e \, x$ .

The commuting condition (for the lower triangle) means that the two animations coincide for all $x \in B$ and $t \in I$ :

$h (x, t) = \tilde h (i \,x, t)$

Just like a fiber is an epitome of non-injectiveness, one can define a cofiber as an epitome of non-surjectiveness. It’s essentially the part of $E$ that is not covered by $i$ .

As a topological space it’s the result of shrinking the image of $B$ inside $E$ to a point (the resulting topology is called the quotient topology).

Notice that, unlike with fibers, there is just one cofiber for a given cofibration (up to homotopy equivalence).

Lifting Property

A category theorist looking at the two diagrams that define, respectively, homotopy lifting and extension, will immediately ignore all the superfluous details. She will turn the second diagram upside down and merge it with the first diagram to get:

This is how we read the new diagram: If for any morphisms $f$ and $g$ that make the outer square commute, there exist a diagonal morphism $h$ that makes the two triangles commute, then we say that $i$ has the left lifting property with respect to $p$ . Equivalently, $p$ has the right lifting property with respect to $i$ .

Or we can say that the two morphisms are orthogonal to each other.

The motivation for this nomenclature is interesting. In the category of sets, the archetypal non-surjective function is the “absurd” $0 \to 1$ (or, in set notation, $\emptyset \to \{*\}$ ). It turns out that all surjective functions are its right liftings. In other words, all surjections are right-orthogonal to the simplest non-surjective function.

Indeed, the function at the bottom $y \colon 1 \to Y$ picks an element $y \in Y$ . Similarly, the diagonal function picks an element $x \in X$ . The commuting triangle tells us that for every $y$ there exists an $x$ such that $y = p \, x$ .

Similarly, we can show that all injective functions are orthogonal to the archetypal non-injective function $2 \to 1$ (or $\{x_1, x_2\} \to \{*\}$ ).

Indeed, assume that $i$ maps two different elements $a_1, a_2 \in A$ to a single element $b \in B$ . We could then pick $f$ such that $f \, a_1 = x_1$ and $f \, a_2 = x_2$ . The diagonal $h$ can map $b$ to either $x1$ or $x2$ but not both, so we couldn’t make the upper triangle commute.