Bartosz Milewski's Programming Cafe

Previously: Sheaves as Virtual Objects.

In order to define a sheaf, we have to start with coverage. A coverage defines, for every object , a family of covers that satisfy the sub-coverage conditions. Granted, we can express coverage using objects and arrows, but it would be much nicer if we could use the language of functors and natural transformations.

Let’s start with the idea that, categorically, a cover of is a bunch of arrows converging on . Each arrow is a member of the hom-set . Now consider the fact that is a presheaf, , and ask the question: Is a cover a “subfunctor” of ?

A subfunctor of a presheaf 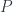is defined as a functor 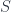such that, for each object , is a subset of and, for each arrow , the function is a restriction of .

In general, a cover does not correspond to a subfunctor of the hom-functor. Let’s see why, and how we can fix it.

Let’s try to define 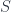, such that is non-empty for any object that’s in the cover of , and empty otherwise. As a presheaf, we could represent it as a virtual object with arrows coming from all ‘s.

Now consider an object that is not in the cover, but it has an arrow connecting it to some element of the cover. Functoriality requires the (virtual) composition to exist.

Thus must be included in the cover–if we want 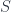to be a functor.

In particular, if we are looking at a category of open sets with inclusions, this condition means that all (open) sub-sets of the covering sets must also be included in the cover. Such a “downward closed” family of sets is called a sieve.

Imagine sets in the cover as holes in a sieve. Smaller sets that can “pass through” these holes must also be parts of the sieve.

If you start with a cover, you can always extend it to a covering sieve by adding more arrows. It’s as if you started with a few black holes, and everything that could fall into them, would fall.

We have previously defined sheaves in terms of coverings. In the next installment we’ll see that they can equally well be defined using covering sieves.

Next Sieves and Sheaves.

Previously: Coverages and Sites

The definition of a sheaf is rather complex and involves several layers of abstraction. To help us navigate this maze we can use some useful intuitions. One such intuition is to view objects in our category as some kind of sets (in particular, open sets, when we talk about topology), and arrows as set inclusions. An arrow from to means that is a subset of .

A cover of is a family of arrows . A coverage assigns a collection of covers to every object, satisfying the sub-coverage conditions described in the previous post. A category with coverage is called a site.

The next layer of abstraction deals with presheaves, which are set-valued contravariant functors. Interestingly, there is a way to interpret a presheaf as an extension of the original category. I learned this trick from Paolo Perrone.

We may represent a presheaf 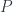using virtual hom-sets. First we add one virtual object, let’s call it , to our category. The set is then interpreted as the set of arrows from to .

Moreover, we can represent the action of 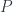on arrows as simple composition. Take an arrow . The presheaf lifts it to a function between sets: (contravariance means that the arrow is reversed). For any we can define the composition 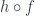to be .

Incidentally, if the functor 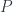is representable, it means that we can replace the virtual object with an actual object in our category.

Notice that, even though the category of open sets with inclusions is a poset (hom-sets are either singletons or empty, and all diagrams automatically commute), the added virtual hom-sets usually contain lots of arrows. In topology these hom-sets are supposed to represent sets of continuous functions over open sets.

We can interpret the virtual object as representing an imaginary open set that “includes” all the objects for which is non-empty, but we have to imagine that it’s possible to include an object in more than one way, to account for multiple arrows. In fact, in what follows we won’t be assuming that the underlying category is a poset, so virtual hom-sets are nothing special.

To express the idea of intersections of open sets, we use commuting diagrams. For every pair of objects and that are in the cover of ,  an object is in their intersection if  the following diagram commutes:

Note that in a poset all diagrams commute, but here we’re generalizing this condition to an arbitrary category. We could say that is in the intersection of and seen as covers of .

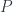Equipped with this new insight, we can now express the sheaf condition. We assume that there is a coverage defined in our category. We are adding one more virtual object for the presheaf , with bunches of virtual arrows pointing to it.

For every cover we try to select a family of virtual arrows, . It’s as if the objects , besides covering , also covered the virtual object .

We call the family a matching family, if this new covering respects the existing intersections. If is in the intersection of and (as covers of , see the previous diagram), then we want the following diagram to also commute:

In other words, the ‘s intersect as covers of .

A presheaf 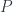is a sheaf if, for every covering family and every matching family 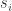there exists a unique that factorizes those 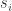‘s:

Translating it back to the language of topology: There is a unique global function defined over whose restrictions are 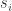‘s.

The advantage of this approach is that it’s easy to imagine the sheafification of an arbitrary presheaf by freely adding virtual arrows (the ‘s and their compositions with ‘s in the above diagram) to all intersection diagrams.

Next: Covering Sieves

Previously: Sheaves and Topology.

In our quest to rewrite topology using the language of category theory we introduced the category of open sets with set inclusions as morphisms. But when we needed to describe open covers, we sort of cheated: we chose to talk about set unions. Granted, set unions can be defined as coproducts in this category (not to be confused with coproducts in the category of sets and functions, where they correspond to disjoint unions). This poset of open sets with finite products and infinite coproducts is called a frame. There is however a more general definition of coverage that is applicable to categories that are not necessarily posets.

A cover of an open set is a family of open sets that doesn’t leave any part of uncovered. In terms of inclusions, we can rephrase this as having a family of of morphisms . But then how do we ensure that these sets indeed cover the whole of ?

The familiar trick of category theory is to look at the totality of all covers. Suppose that for every open set we have not one, but a whole collection of covers: that is a collection of families , each indexed by a potentially different set .

Now consider an open subset . If the family is a cover of than the family of intersections should form a cover of .

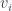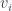Indeed, an intersection of two open sets is again an open set, so all ‘s are automatically open. And if no part of was left uncovered by ‘s, then no part of is left uncovered by ‘s.

Conversely, imagine that we had an incomplete cover, with a hole large enough to stick an open set in it. The empty intersection of that “cover” with would then produce no cover of . So the requirement that each cover produces a smaller sub-cover eliminates the possibility of substantial holes in coverage. This is good enough for our generalization.

We are now ready to define coverage using categorical language. We just have to make sure that this definition reproduces the set-theoretic picture when we replace objects with open sets, and arrows with inclusions.

A coverage 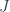on a category 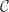assigns to each object a collection of families of arrows .

For every such family , and every object equipped with an arrow , there exist a covering family that is a sub-family of .

This means that for every we can find its “parent” , i.e., every inclusion can be factored through some :

A category with a coverage is called a site. As we’ve seen before, the definition of a sheaf uses a coverage, so a site provides the minimum of structure for a sheaf.

For completeness, here’s the definition of a sheaf on a site as explained in detail in the previous post:

Our starting point is a presheaf , abstracting the idea of assigning a set of functions to every open set (an object of 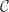). 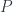maps arrows in 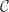(inclusions of open sets) to restrictions of said functions. This presheaf is a sheaf if:

• For every covering family
• and every compatible family (tuple) of elements , such that for every that has arrows to two objects: and , such that , we have:
  

  (the restrictions on all overlaps coincide)

• there is a unique element such that for all (we can collate all individual functions).

As you’d expect in topology, this definition doesn’t mention sizes or distances. More interestingly, we don’t talk about points. Normally a topological space is defined as a set of points, and so are open sets. The categorical language lets us talk about point-free topologies.

There is a further generalization of sheaves, where the target of the functor 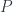is not but a category with some additional structure. This makes sense, because the set of functions defined over an open set has usually more structure. It’s the structure induced by the target of these functions. For instance real- or complex-valued functions can be added, subtracted, and multiplied–point-wise. Division of functions is not well defined because of zeros, so they only form a ring.

There is an intriguing possibility that the definition of a coverage could be used to generalize convolutional neural networks (CNN). For instance, voice or image recognition involves applying a sliding window to the input. This is usually done using fixed-sized (square) window, but what really matters is that the input is covered by overlapping continuous areas that capture the 2-dimensional (topological) nature of the input. The same idea can be applied to higher dimensional data. In particular, we can treat time as an additional dimension, capturing the idea of continuous motion.

Next Sheaves as Virtual Objects.