In my previous blog post, Programming with Universal Constructions, I mentioned in passing that one-to-one mappings between sets of morphisms are often a manifestation of adjunctions between functors. In fact, an adjunction just extends a universal construction over the whole category (or two categories, in general). It combines the mapping-in with the mapping-out conditions. One functor (traditionally called the left adjoint) prepares the input for mapping out, and the other (the right adjoint) prepares the output for mapping in. The trick is to find a pair of functors that complement each other: there are as many mapping-outs from one functor as there are mapping-ins to the other functor.
To gain some insight, let’s dig deeper into the examples from my previous post.
The defining property of a product was the universal mapping-in condition. For every object equipped with a pair of morphisms going to, respectively,
and
, there was a unique morphism
mapping
to the product
. The commuting condition ensured that the correspondence went both ways, that is, given an
, the two morphisms were uniquely determined.
A pair of morphisms can be seen as a single morphism in a product category . So, really, we have an isomorphism between hom-sets in two categories, one in
and the other in
. We can also define two functors going between these categories. An arbitrary object
in
is mapped by the diagonal functor
to a pair
in
. That’s our left functor. It prepares the source for mapping out. The right functor maps an arbitrary pair
to the product
in
. That’s our target for mapping in.
The adjunction is the (natural) isomorphism of the two hom-sets:
Let’s develop this intuition. As usual in category theory, an object is defined by its morphisms. A product is defined by the mapping-in property, the totality of morphisms incoming from all other objects. Hence we are interested in the hom-set between an arbitrary object and our product
. This is the right hand side of the picture. On the left, we are considering the mapping-out morphism from the object
, which is the result of applying the functor
to
. Thus an adjunction relates objects that are defined by their mapping-in property and objects defined by their mapping-out property.
Another way of looking at the pair of adjoint functors is to see them as being approximately the inverse of each other. Of course, they can’t, because the two categories in question are not isomorphic. Intuitively, is “much bigger” than
. The functor that assigns the product
to every pair
cannot be injective. It must map many different pairs to the same (up to isomorphism) product. In the process, it “forgets” some of the information, just like the number 12 forgets whether it was obtained by multiplying 2 and 6 or 3 and 4. Common examples of this forgetfulness are isomorphisms such as
or
Since the product functor loses some information, its left adjoint must somehow compensate for it, essentially by making stuff up. Because the adjunction is a natural transformation, it must do it uniformly across the whole category. Given a generic object , the only way it can produce a pair of objects is to duplicate
. Hence the diagonal functor
. You might say that
“freely” generates a pair. In almost every adjunction you can observe this interplay of “freeness” and “forgetfulness.” I’m using these therm loosely, but I can be excused, because there is no formal definition of forgetful (and therefore free or cofree) functors.
Left adjoints often create free stuff. The mnemonic is that “the left” is “liberal.” Right adjoints, on the other hand, are “conservative.” They only use as much data as is strictly necessary and not an iota more (they also preserve limits, which the left adjoints are free to ignore). This is all relative and, as we’ll see later, the same functor may be the left adjoint to one functor and the right adjoint to another.
Because of this lossiness, a round trip using both functors doesn’t produce an identity. It is however “related” to the identity functor. The combination left-after-right produces an object that can be mapped back to the original object. Conversely, right-after-left has a mapping from the identity functor. These two give rise to natural transformations that are called, respectively, the counit and the unit
.
Here, the combination diagonal functor after the product functor takes a pair to the pair
. The counit
then maps it back to
using a pair of projections
(which is a single morphism in
). It’s easy to see that the family of such morphisms defines a natural transformation.
If we think for a moment in terms of set elements, then for every element of the target object, the counit extracts a pair of elements of the source object (the objects here are pairs of sets). Note that this mapping is not injective and, therefore, not invertible.
The other composition–the product functor after the diagonal functor–maps an object to
. The component of the unit natural transformation,
, is implemented using the universal property of the product. Indeed, such a morphism is uniquely determined by a pair of identity morphsims
. Again, when we vary
, these morphisms combine to form a natural transformation.
Thinking in terms of set elements, the unit inserts an element of the set in the target set. And again, this is not an injective map, so it cannot be inverted.
Although in an arbitrary category we cannot talk about elements, a lot of intuitions from carry over to a more general setting. In a category with a terminal object, for instance, we can talk about global elements as mappings from the terminal object. In the absence of the terminal object, we may use other objects to define generalized elements. This is all in the true spirit of category theory, which defines all properties of objects in terms of morphisms.
Every construction in category theory has its dual, and the product is no exception.
A coproduct is defined by a mapping out property. For every pair of morphisms from, respectively, and
to the common target
there is a unique mapping out from the coproduct
to
. In programming, this is called case analysis: a function from a sum type is implemented using two functions corresponding to two cases. Conversely, given a mapping out of a coproduct, the two functions are uniquely determined due to the commuting conditions (this was all discussed in the previous post).
As before, this one-to-one correspondence can be neatly encapsulated as an adjunction. This time, however, the coproduct functor is the left adjoint of the diagonal functor.
The coproduct is still the “forgetful” part of the duo, but now the diagonal functor plays the role of the cofree funtor, relative to the coproduct. Again, I’m using these terms loosely.
The counit now works in the category and it “extracts a value” from the symmetric coproduct of
with
. It does it by “pattern matching” and applying the identity morphism.
The unit is more interesting. It’s built from two injections, or two constructors, as we call them in programming.
I find it fascinating that the simple diagonal functor can be used to define both products and coproducts. Moreover, using terse categorical notation, this whole blog post up to this point can be summarized by a single formula.
That’s the power of adjunctions.
There is one more very important adjunction that every programmer should know: the exponential, or the currying adjunction. The exponential, a.k.a. the function type, is the right adjoint to the product functor. What’s the product functor? Product is a bifunctor, or a functor from to
. But if you fix one of the arguments, it just becomes a regular functor. We’re interested in the functor
or, more explicitly:
It’s a functor that multiplies its argument by some fixed object . We are using this functor to define the exponential. The exponential
is defined by the mapping-in property. The mappings out of the product
to
are in one to one correspondence with morphisms from an arbitrary object
to the exponential
.
The exponential is an object representing the set of morphisms from
to
, and the two directions of the isomorphism above are called curry and uncurry.
This is exactly the meaning of the universal property of the exponential I discussed in my previous post.
The counit for this adjunction extracts a value from the product of the function type (the exponential) and its argument. It’s just the evaluation morphism: it applies a function to its argument.
The unit injects a value of type into a function type
. The unit is just the curried version of the product constructor.
I want you to look closely at this formula through your programming glasses. The target of the unit is the type:
b -> (c, b)
You may recognize it as the state monad, with b representing the state. The unit is nothing else but the natural transformation whose component we call return. Coincidence? Not really! Look at the component of the counit:
(b -> a, b) -> a
It’s the extract of the Store comonad.
It turns out that every adjunction gives rise to both a monad and a comonad. Not only that, every monad and every comonad give rise to adjunctions.
It seems like, in category theory, if you dig deep enough, everything is related to everything in some meaningful way. And every time you revisit a topic, you discover new insights. That’s what makes category theory so exciting.








September 20, 2019 at 3:57 pm
Thank you for post. As usual very interesting.
I think there is small typo: “Here, the diagonal functor after the product functor takes a pair \langle a, b\rangle to the pair \langle a \times b, a \times b\rangle” should be “Here, the diagonal functor after the product functor takes a product a \times b to the pair \langle a \times b, a \times b\rangle”. The diagonal functor maps a product object, not a pair in source category.
September 20, 2019 at 4:44 pm
I see how it might be confusing. I mean “after” as the composition of two functors. Maybe I should parenthesize it.
September 24, 2019 at 2:29 am
In the adjunction that defines the product, the unit is given by c -> c x c which, in Haskell, is unit c = (c, c). How can we now define a join for the monad (x) . Delta?
September 24, 2019 at 10:50 am
The monad is not the product but the product after delta. So join has the signature
join :: ((c, c), (c, c)) -> (c, c)and implementationjoin = bimap fst snd(it has to satisfy unit laws).September 27, 2019 at 8:01 am
So, in this case, the join of the monad is the same as the counit of the comonad?
Or am I completely lost and mixing things?
September 27, 2019 at 11:12 am
Not really, but close. Join is obtained from counit by sandwiching it between left and right functor . (see Modnads Categorically.
. (see Modnads Categorically.
September 27, 2019 at 12:47 pm
Thanks for another great post! I’ve been trying to make progress understanding adjunctions for a long time and this post finally fit a bunch of things into place for me. Much thanks
September 27, 2019 at 4:46 pm
Yes, mu = R . eta . L but here it is when I have lots of problems finding the composition.
In our case, R = () and L = Delta, so mu = () . eta . Delta.
But both () and Delta are functors, so if we only want to express the composition using natural transformations, we have to do mu = I_() . eta . I_Delta, where the I’s are the identity natural transformation acting on the given functors.
And, as it is stated in the post, eta :: () . Delta ~> I (identity functor in CC)
So, the composed functors in the upper part are: () . Delta . () . Delta; and the composed functor on the bottom part are: () . I . Delta, which is () . Delta.
Good, the types correspond to the join of the monad (*) . Delta. [Until here I’m pretty sure I’m on the right track, but maybe I’m wrong]
Now, I try to get the components of these natural transformations.
I_Delta is the identity on Delta, so it is Delta ~> Delta, which can be expressed as: I_Delta c :: Delta c -> Delta c, which has type (c, c) -> (c, c).
I_() is the identity on (), so is () ~> () but () is a functor in CxC so it’s components are pairs of functions. So its components I_() (c1,c2) :: (c1, c2) -> (c1, c2) which is the pair of functions (c1->c1, c2->c2)
eta :: Delta . (*) ~> I where both functors are in CxC, so in components, we have eta (c1, c2) :: ((c1, c2), (c1, c2)) -> (c1, c2) which is, as shown in the post, the pair of functions (fst, snd)
On the one hand, it seems that all the functions are identities, except eta, so my initial supposition of mu = eta holds.
But, on the other hand, I’m unable to do the composition formally and I cannot prove what my supposition is.
Thanks four your patience reading such a long comment !!!
September 27, 2019 at 4:50 pm
WP has substituted some of the (*) in my comment by (). I hope it is already readable.
What a mess 😦
September 27, 2019 at 8:07 pm
This should really be a separate blog post. But since I started it, I feel obliged to explain. So the main idea is that horizontal composition with a functor is called whiskering and it works differently on the left and on the right.
If the functor is on the right, you instantiate the natural transformation at the result of the functor. Here, the component of the counit at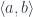 is a morphism
is a morphism  . Actually, it’s a pair of morphisms
. Actually, it’s a pair of morphisms  .
.
When you whisker it with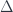 on the right, you instantiate it at the diagonal. So
on the right, you instantiate it at the diagonal. So  .
.
Whiskering on the left takes a natural transformation and lifts it using the functor. Here, the functor is the product and it takes a pair of objects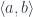 to
to 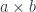 . It also lifts a pair of morphisms using
. It also lifts a pair of morphisms using
bimap. This is why you getjoin = bimap fst snd. Notice that whiskering on the right is reflected in the type signature, while whiskering on the left is reflected in code.I hope this helps.
September 28, 2019 at 1:06 am
Working with diagrams is usually “simple”, but doing the plumbing required to translate them to code can be, at leas for mi, much harder.
Many, many, many thanks !!!
October 8, 2019 at 10:07 am
Hi Bartosz,
I could not find you email anywhere so I ask you here. Basically I am doing a master in Theoretical CS and I would like to prepare the presentation of a paper in the intersection between Category Theory and Computer Science.
For example I thought about “Compiling to Categories”, any other suggestion?
Thanks!
October 8, 2019 at 10:25 am
Conal Elliott’s compiling to categories sounds great.
December 17, 2019 at 11:37 pm
[…] Перевод статьи Бартоша Милевски «The Power of Adjunctions» (исходный текст расположен по адресу — Текст оригинальной статьи). […]
January 6, 2020 at 10:08 pm
[…] The power of adjunctions. ~ Bartosz Milewski. #CategoryTheory #Programming […]